STATISTIQUE DESCRIPTIVE LMENTAIRE Jeanne Fine Professeure de Statistique

STATISTIQUE DESCRIPTIVE ÉLÉMENTAIRE Jeanne Fine Professeure de Statistique, Université de Toulouse jeanne. fine@math. univ-toulouse. fr Jeanne Fine http: //finestat. free. fr Statistique descriptive

La statistique descriptive élémentaire consiste à effectuer le traitement statistique des variables une par une (statistique unidimensionnelle ou « tri à plat » ) ou deux par deux (statistique bidimensionnelle ou « tri croisé » ). L’existence de deux types de variables, catégorielle et réelle, conduit à considérer cinq traitements statistiques de base. C'est le plan du cours St@ternet, installé en libre accès sur le site pédagogique de l’IUFM Midi-Pyrénées et téléchargeable, dont on donne un extrait dans ce document : http: //www 2. toulouse. iufm. fr/mathematiques/ Jeanne Fine http: //finestat. free. fr Statistique descriptive 2

PLAN DU COURS 1. Introduction : un exemple 2. Traitement statistique d’une variable catégorielle 3. Traitement statistique d’une variable réelle 4. Traitement statistique de deux variables catégorielles 5. Traitement statistique de deux variables réelles 6. Traitement statistique d'une variable catégorielle et d'une variable réelle Jeanne Fine http: //finestat. free. fr Statistique descriptive 3

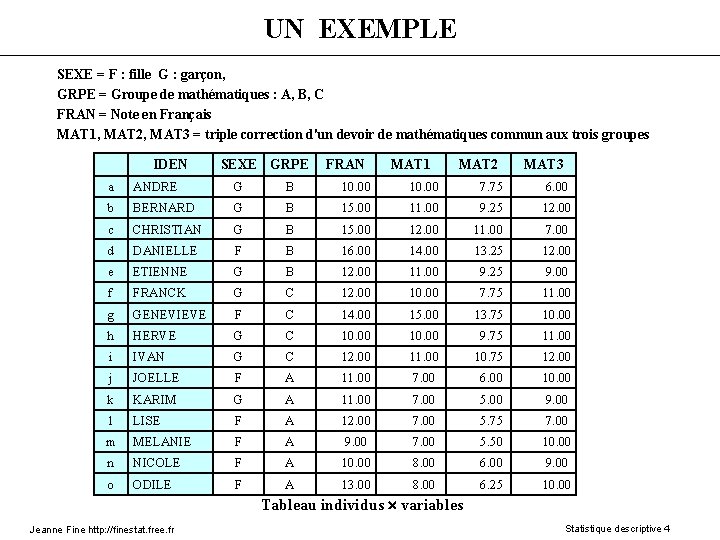
UN EXEMPLE SEXE = F : fille G : garçon, GRPE = Groupe de mathématiques : A, B, C FRAN = Note en Français MAT 1, MAT 2, MAT 3 = triple correction d'un devoir de mathématiques commun aux trois groupes IDEN SEXE GRPE FRAN MAT 1 MAT 2 MAT 3 a ANDRE G B 10. 00 7. 75 6. 00 b BERNARD G B 15. 00 11. 00 9. 25 12. 00 c CHRISTIAN G B 15. 00 12. 00 11. 00 7. 00 d DANIELLE F B 16. 00 14. 00 13. 25 12. 00 e ETIENNE G B 12. 00 11. 00 9. 25 9. 00 f FRANCK G C 12. 00 10. 00 7. 75 11. 00 g GENEVIEVE F C 14. 00 15. 00 13. 75 10. 00 h HERVE G C 10. 00 9. 75 11. 00 i IVAN G C 12. 00 11. 00 10. 75 12. 00 j JOELLE F A 11. 00 7. 00 6. 00 10. 00 k KARIM G A 11. 00 7. 00 5. 00 9. 00 l LISE F A 12. 00 7. 00 5. 75 7. 00 m MELANIE F A 9. 00 7. 00 5. 50 10. 00 n NICOLE F A 10. 00 8. 00 6. 00 9. 00 o ODILE F A 13. 00 8. 00 6. 25 10. 00 Tableau individus variables Jeanne Fine http: //finestat. free. fr Statistique descriptive 4

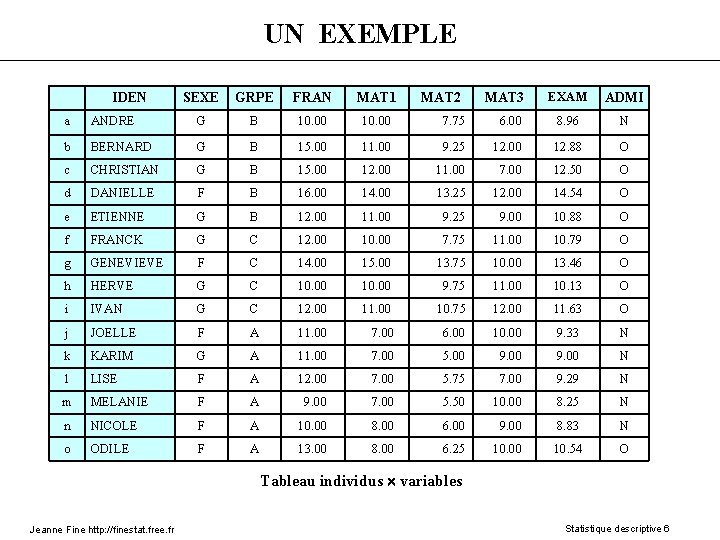
UN EXEMPLE Construction de nouvelles variables variable MATH : MATH = (MAT 1 + MAT 2 + MAT 3) variable EXAM : EXAM = (FRAN + MATH) variable ADMI : si EXAM 10 alors ADMI = O, sinon ADMI = N Jeanne Fine http: //finestat. free. fr Statistique descriptive 5

UN EXEMPLE IDEN SEXE GRPE FRAN MAT 1 MAT 2 MAT 3 EXAM ADMI a ANDRE G B 10. 00 7. 75 6. 00 8. 96 N b BERNARD G B 15. 00 11. 00 9. 25 12. 00 12. 88 O c CHRISTIAN G B 15. 00 12. 00 11. 00 7. 00 12. 50 O d DANIELLE F B 16. 00 14. 00 13. 25 12. 00 14. 54 O e ETIENNE G B 12. 00 11. 00 9. 25 9. 00 10. 88 O f FRANCK G C 12. 00 10. 00 7. 75 11. 00 10. 79 O g GENEVIEVE F C 14. 00 15. 00 13. 75 10. 00 13. 46 O h HERVE G C 10. 00 9. 75 11. 00 10. 13 O i IVAN G C 12. 00 11. 00 10. 75 12. 00 11. 63 O j JOELLE F A 11. 00 7. 00 6. 00 10. 00 9. 33 N k KARIM G A 11. 00 7. 00 5. 00 9. 00 N l LISE F A 12. 00 7. 00 5. 75 7. 00 9. 29 N m MELANIE F A 9. 00 7. 00 5. 50 10. 00 8. 25 N n NICOLE F A 10. 00 8. 00 6. 00 9. 00 8. 83 N o ODILE F A 13. 00 8. 00 6. 25 10. 00 10. 54 O Tableau individus variables Jeanne Fine http: //finestat. free. fr Statistique descriptive 6

2. TRAITEMENT STATISTIQUE D’UNE VARIABLE CATÉGORIELLE 2. 1. Partition de la population engendrée par la variable Jeanne Fine http: //finestat. free. fr Statistique descriptive 7

2. TRAITEMENT STATISTIQUE D’UNE VARIABLE CATÉGORIELLE 2. 2. Distribution d'effectifs et de fréquences GRPE Effectifs Fréquences B 5 33% C 4 27% A 6 40% Ensemble 15 100% Distributions des effectifs et des fréquences de la variable GRPE Jeanne Fine http: //finestat. free. fr Statistique descriptive 8

2. TRAITEMENT STATISTIQUE D’UNE VARIABLE CATÉGORIELLE 2. 3. Représentation graphique : diagrammes en barres ou en secteurs Diagramme en barres des effectifs et des fréquences de la variable GRPE Jeanne Fine http: //finestat. free. fr Diagramme en secteurs des fréquences de la variable GRPE Statistique descriptive 9

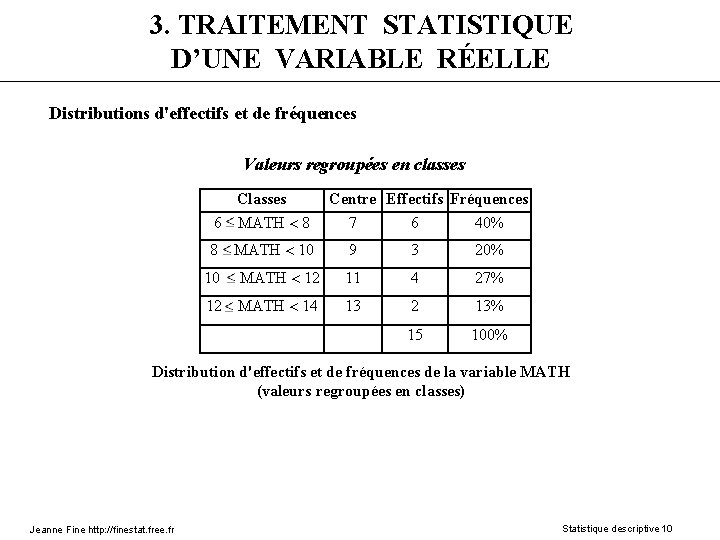
3. TRAITEMENT STATISTIQUE D’UNE VARIABLE RÉELLE Distributions d'effectifs et de fréquences Valeurs regroupées en classes Classes 6 MATH 8 Centre Effectifs Fréquences 7 6 40% 8 MATH 10 9 3 20% 10 MATH 12 11 4 27% 12 MATH 14 13 2 13% 15 100% Distribution d'effectifs et de fréquences de la variable MATH (valeurs regroupées en classes) Jeanne Fine http: //finestat. free. fr Statistique descriptive 10

3. TRAITEMENT STATISTIQUE D’UNE VARIABLE RÉELLE Représentation graphique : l'histogramme Dans le cas où les amplitudes sont différentes, il faut veiller à construire des rectangles dont les aires soient proportionnelles aux effectifs (ou aux fréquences). Jeanne Fine http: //finestat. free. fr Statistique descriptive 11

3. TRAITEMENT STATISTIQUE D’UNE VARIABLE RÉELLE Résumés numériques : indices de position et de dispersion • Mode et étendue Le mode est la valeur de la variable correspondant au plus grand effectif. L’étendue est la différence entre la plus grande et la plus petite valeur de la variable. Jeanne Fine http: //finestat. free. fr Statistique descriptive 12

3. TRAITEMENT STATISTIQUE D’UNE VARIABLE RÉELLE • Moyenne, variance et écart-type La moyenne (arithmétique) est la valeur commune à chaque individu s’ils avaient tous la même valeur. La variance est la moyenne des carrés des écarts à la moyenne. La variance est aussi la moyenne des carrés moins le carré de la moyenne. L’écart-type est la racine carrée de la variance. Jeanne Fine http: //finestat. free. fr Statistique descriptive 13

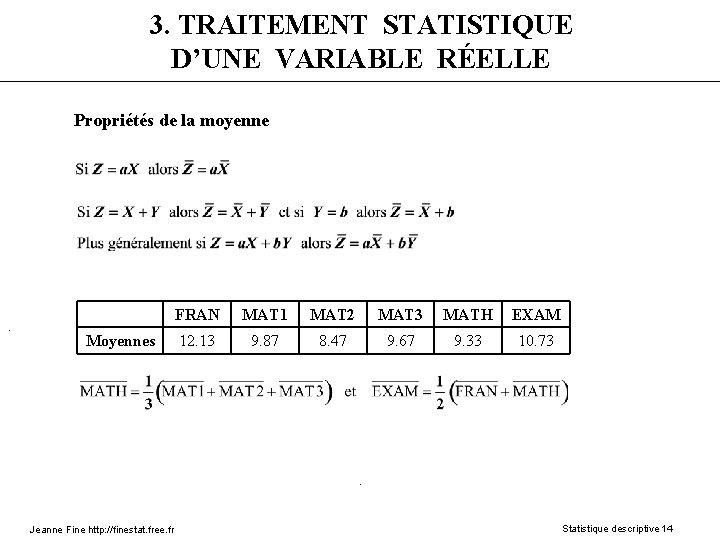
3. TRAITEMENT STATISTIQUE D’UNE VARIABLE RÉELLE Propriétés de la moyenne . Moyennes FRAN MAT 1 MAT 2 MAT 3 MATH EXAM 12. 13 9. 87 8. 47 9. 67 9. 33 10. 73 . Jeanne Fine http: //finestat. free. fr Statistique descriptive 14

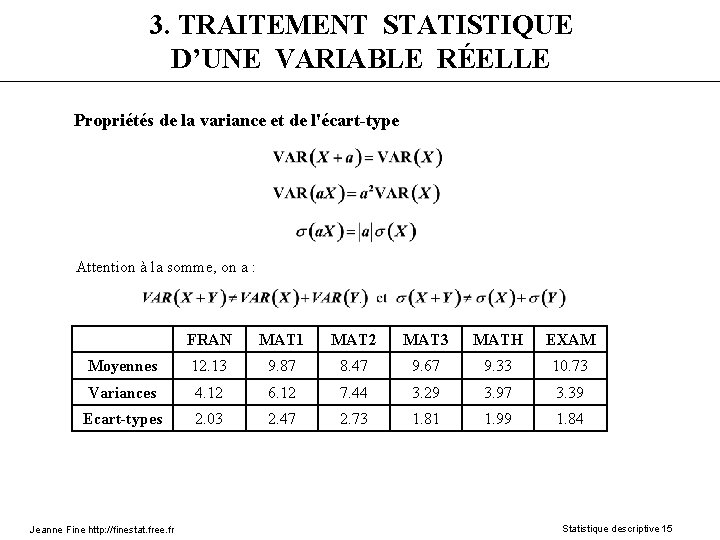
3. TRAITEMENT STATISTIQUE D’UNE VARIABLE RÉELLE Propriétés de la variance et de l'écart-type Attention à la somme, on a : . FRAN MAT 1 MAT 2 MAT 3 MATH EXAM Moyennes 12. 13 9. 87 8. 47 9. 67 9. 33 10. 73 Variances 4. 12 6. 12 7. 44 3. 29 3. 97 3. 39 Ecart-types 2. 03 2. 47 2. 73 1. 81 1. 99 1. 84 Jeanne Fine http: //finestat. free. fr Statistique descriptive 15

3. TRAITEMENT STATISTIQUE D’UNE VARIABLE RÉELLE Une variable dont la moyenne est égale à 0 est dite centrée. Une variable dont l'écart-type est égal à 1 est dite réduite. Jeanne Fine http: //finestat. free. fr Statistique descriptive 16

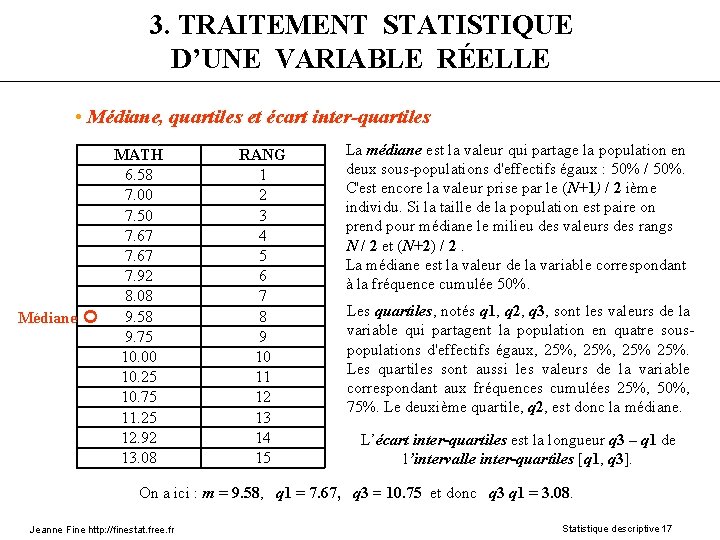
3. TRAITEMENT STATISTIQUE D’UNE VARIABLE RÉELLE • Médiane, quartiles et écart inter-quartiles MATH 6. 58 7. 00 7. 50 7. 67 7. 92 8. 08 9. 58 Médiane 9. 75 10. 00 10. 25 10. 75 11. 25 12. 92 13. 08 RANG 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 La médiane est la valeur qui partage la population en deux sous-populations d'effectifs égaux : 50% / 50%. C'est encore la valeur prise par le (N+1) / 2 ième individu. Si la taille de la population est paire on prend pour médiane le milieu des valeurs des rangs N / 2 et (N+2) / 2. La médiane est la valeur de la variable correspondant à la fréquence cumulée 50%. Les quartiles, notés q 1, q 2, q 3, sont les valeurs de la variable qui partagent la population en quatre souspopulations d'effectifs égaux, 25%, 25%. Les quartiles sont aussi les valeurs de la variable correspondant aux fréquences cumulées 25%, 50%, 75%. Le deuxième quartile, q 2, est donc la médiane. L’écart inter-quartiles est la longueur q 3 – q 1 de l’intervalle inter-quartiles [q 1, q 3]. On a ici : m = 9. 58, q 1 = 7. 67, q 3 = 10. 75 et donc q 3 q 1 = 3. 08. Jeanne Fine http: //finestat. free. fr Statistique descriptive 17

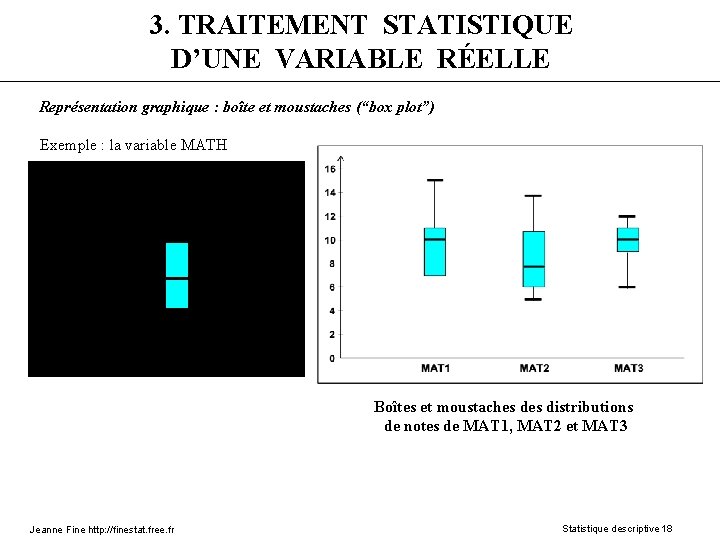
3. TRAITEMENT STATISTIQUE D’UNE VARIABLE RÉELLE Représentation graphique : boîte et moustaches (“box plot”) Exemple : la variable MATH Boîtes et moustaches distributions de notes de MAT 1, MAT 2 et MAT 3 Jeanne Fine http: //finestat. free. fr Statistique descriptive 18

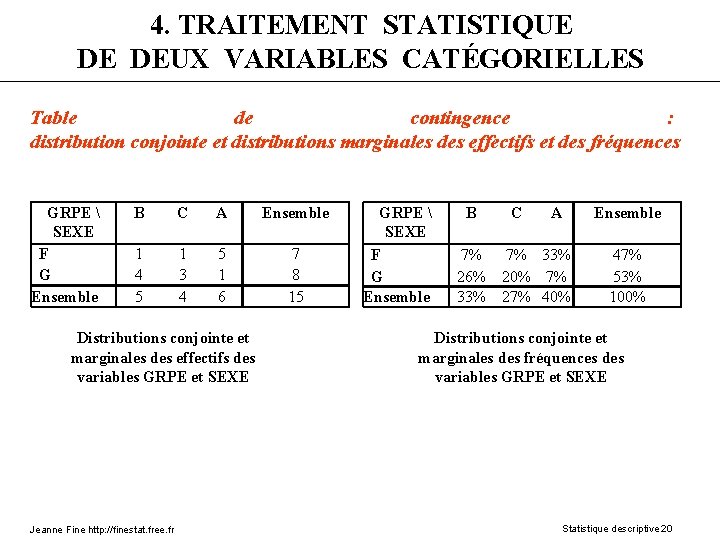
4. TRAITEMENT STATISTIQUE DE DEUX VARIABLES CATÉGORIELLES Partition croisée associée aux deux variables GRPE et SEXE Jeanne Fine http: //finestat. free. fr Statistique descriptive 19

4. TRAITEMENT STATISTIQUE DE DEUX VARIABLES CATÉGORIELLES Table de contingence : distribution conjointe et distributions marginales des effectifs et des fréquences GRPE SEXE F G Ensemble B C A Ensemble 1 4 5 1 3 4 5 1 6 7 8 15 Distributions conjointe et marginales des effectifs des variables GRPE et SEXE Jeanne Fine http: //finestat. free. fr GRPE SEXE F G Ensemble B C A 7% 7% 33% 26% 20% 7% 33% 27% 40% Ensemble 47% 53% 100% Distributions conjointe et marginales des fréquences des variables GRPE et SEXE Statistique descriptive 20

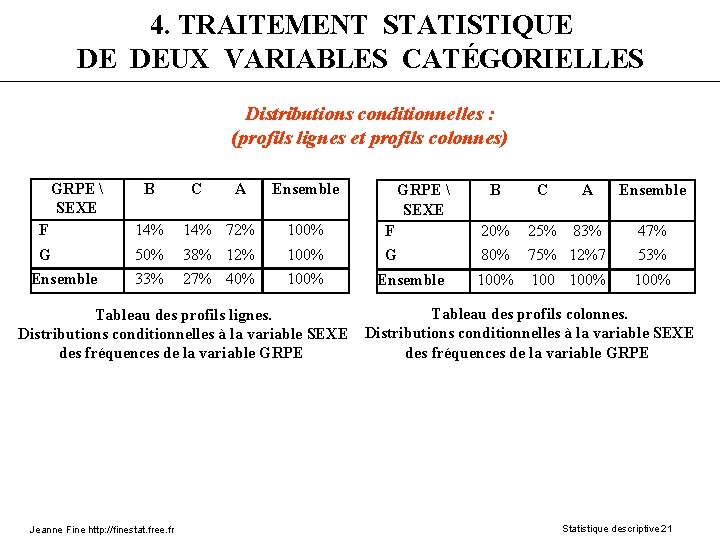
4. TRAITEMENT STATISTIQUE DE DEUX VARIABLES CATÉGORIELLES Distributions conditionnelles : (profils lignes et profils colonnes) GRPE SEXE B C A Ensemble F 14% 72% 100% F 20% 25% 83% 47% G 50% 38% 12% 100% G 80% 75% 12%7 53% Ensemble 33% 27% 40% 100% Ensemble 100% Tableau des profils lignes. Distributions conditionnelles à la variable SEXE des fréquences de la variable GRPE Jeanne Fine http: //finestat. free. fr Tableau des profils colonnes. Distributions conditionnelles à la variable SEXE des fréquences de la variable GRPE Statistique descriptive 21

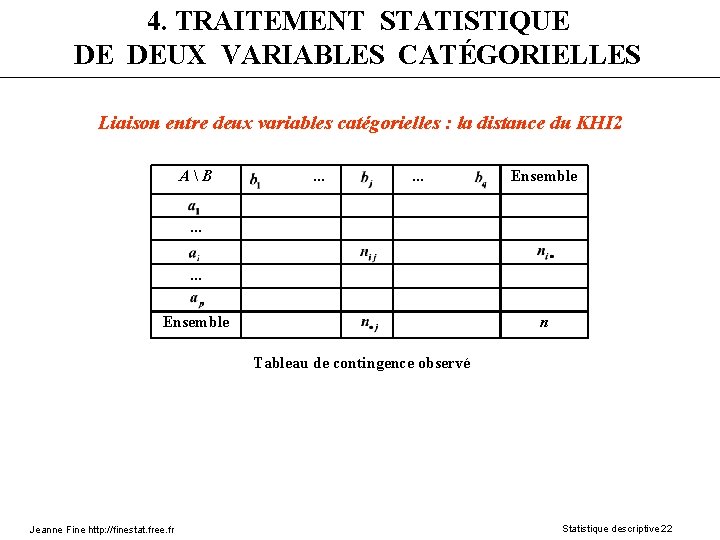
4. TRAITEMENT STATISTIQUE DE DEUX VARIABLES CATÉGORIELLES Liaison entre deux variables catégorielles : la distance du KHI 2 A B . . . Ensemble . . . Ensemble n Tableau de contingence observé Jeanne Fine http: //finestat. free. fr Statistique descriptive 22

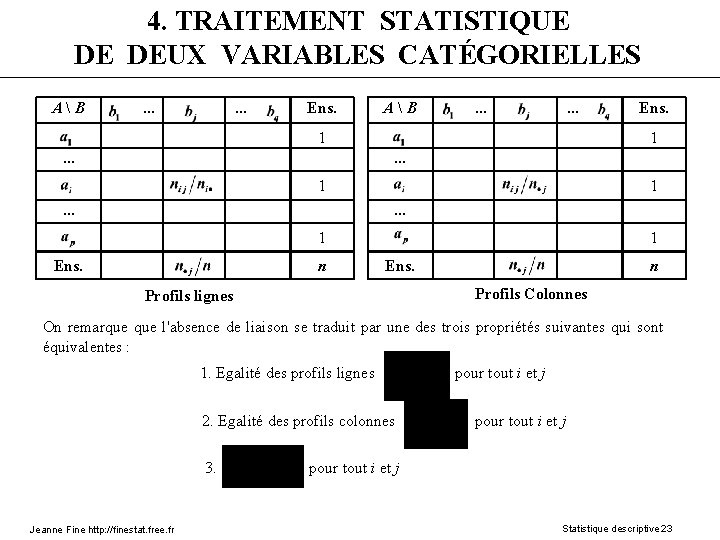
4. TRAITEMENT STATISTIQUE DE DEUX VARIABLES CATÉGORIELLES A B . . . Ens. A B . . . 1. . . Ens. 1 . . . 1 Ens. n 1 Ens. Profils lignes n Profils Colonnes On remarque l'absence de liaison se traduit par une des trois propriétés suivantes qui sont équivalentes : 1. Egalité des profils lignes pour tout i et j 2. Egalité des profils colonnes pour tout i et j 3. pour tout i et j Jeanne Fine http: //finestat. free. fr Statistique descriptive 23

4. TRAITEMENT STATISTIQUE DE DEUX VARIABLES CATÉGORIELLES Le tableau de contingence théorique d'absence de liaison, construit sur les mêmes marges que le tableau de contingence observé, est alors le suivant : A B . . . Ensemble . . . Ensemble n Indice du Khi 2 Jeanne Fine http: //finestat. free. fr Statistique descriptive 24

4. TRAITEMENT STATISTIQUE DE DEUX VARIABLES CATÉGORIELLES Autres formules du KHI 2 Si on introduit les fréquences on a alors : Indice du PHI 2 Le KHI 2 est proportionnel à N. On peut alors introduire l'indice du PHI 2 égal au KHI 2 divisé par n. On obtient pour les variables GRPE et SEXE : KHI 2 = 5. 42 et PHI 2 = 0. 36. Jeanne Fine http: //finestat. free. fr Statistique descriptive 25

5. TRAITEMENT STATISTIQUE DE DEUX VARIABLES RÉELLES Représentation graphique : le graphe plan Graphe plan des variables MAT 1 et MAT 2 L'ensemble des points, appelé nuage des points, est très étiré et assez rectiligne. Les deux variables MAT 1 et MAT 2 sont fortement liées. Jeanne Fine http: //finestat. free. fr Statistique descriptive 26

5. TRAITEMENT STATISTIQUE DE DEUX VARIABLES RÉELLES Résumés numériques : covariance, coefficient de corrélation linéaire • La Covariance La covariance de deux variables réelles X et Y est à la moyenne des produits des différences à la moyenne. La covariance est aussi égale à la moyenne des produits moins le produit des moyennes. Jeanne Fine http: //finestat. free. fr Statistique descriptive 27

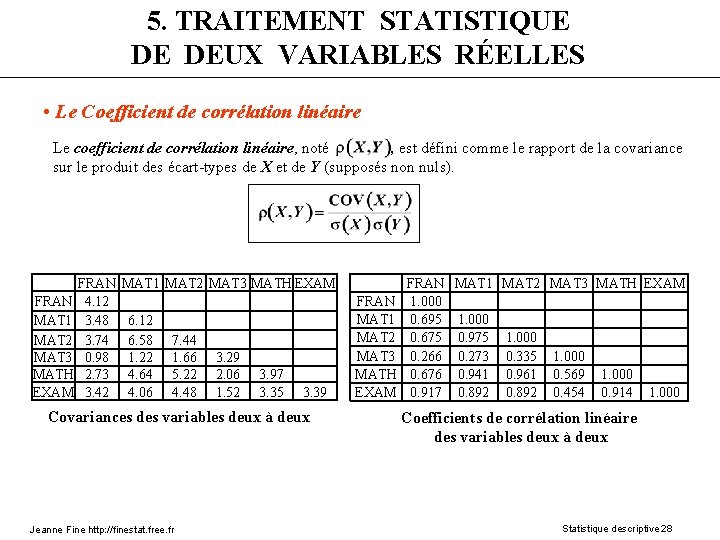
5. TRAITEMENT STATISTIQUE DE DEUX VARIABLES RÉELLES • Le Coefficient de corrélation linéaire Le coefficient de corrélation linéaire, noté , est défini comme le rapport de la covariance sur le produit des écart-types de X et de Y (supposés non nuls). FRAN MAT 1 MAT 2 MAT 3 MATH EXAM FRAN 4. 12 3. 48 3. 74 0. 98 2. 73 3. 42 MAT 1 MAT 2 MAT 3 MATH EXAM 6. 12 6. 58 1. 22 4. 64 4. 06 7. 44 1. 66 5. 22 4. 48 3. 29 2. 06 1. 52 3. 97 3. 35 3. 39 Covariances des variables deux à deux Jeanne Fine http: //finestat. free. fr FRAN MAT 1 MAT 2 MAT 3 MATH EXAM FRAN 1. 000 0. 695 0. 675 0. 266 0. 676 0. 917 MAT 1 MAT 2 MAT 3 MATH EXAM 1. 000 0. 975 0. 273 0. 941 0. 892 1. 000 0. 335 0. 961 0. 892 1. 000 0. 569 0. 454 1. 000 0. 914 1. 000 Coefficients de corrélation linéaire des variables deux à deux Statistique descriptive 28

5. TRAITEMENT STATISTIQUE DE DEUX VARIABLES RÉELLES • Propriétés de la covariance et du coefficient de corrélation linéaire Le coefficient de corrélation linéaire est compris entre 1 et 1. Il est égal à 1 ou 1 si, et seulement si, il existe une relation linéaire entre les variables (d'où son nom). Jeanne Fine http: //finestat. free. fr Statistique descriptive 29

5. TRAITEMENT STATISTIQUE DE DEUX VARIABLES RÉELLES Pour simplifier nous notons X la variable MAT 1 et Y la variable MAT 2. On pose , où E désigne la variable d’erreur ; on cherche a et b rendant minimum la somme (ou la moyenne) des carrés des erreurs (critère de moindre carrés) : La solution est la suivante : Jeanne Fine http: //finestat. free. fr Statistique descriptive 30

5. TRAITEMENT STATISTIQUE DE DEUX VARIABLES RÉELLES La droite ainsi obtenue est dite droite de régression linéaire de Y en X. Jeanne Fine http: //finestat. free. fr Statistique descriptive 31

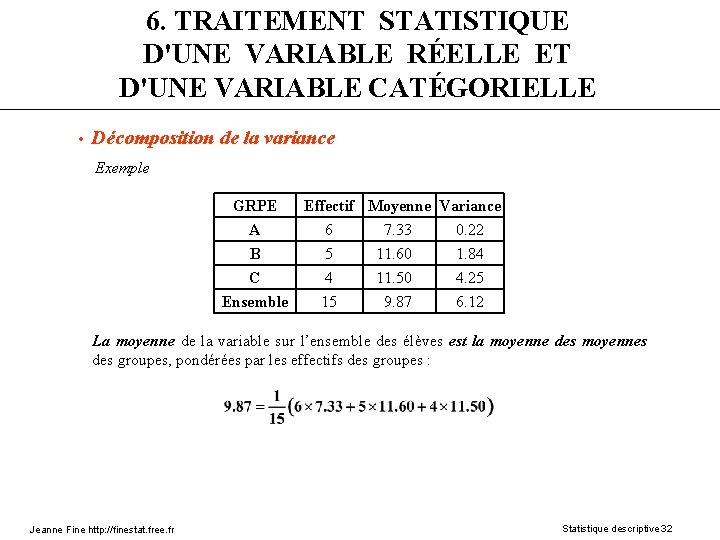
6. TRAITEMENT STATISTIQUE D'UNE VARIABLE RÉELLE ET D'UNE VARIABLE CATÉGORIELLE • Décomposition de la variance Exemple GRPE Effectif Moyenne Variance A 6 7. 33 0. 22 B 5 11. 60 1. 84 C 4 11. 50 4. 25 Ensemble 15 9. 87 6. 12 La moyenne de la variable sur l’ensemble des élèves est la moyenne des moyennes des groupes, pondérées par les effectifs des groupes : Jeanne Fine http: //finestat. free. fr Statistique descriptive 32

6. TRAITEMENT STATISTIQUE D'UNE VARIABLE RÉELLE ET D'UNE VARIABLE CATÉGORIELLE La variance inter-groupes (ou inter-classes) est la variance des moyennes : La variance intra-groupes (ou intra-classes) est la moyenne des variances : La variance de la variable est égale à la somme des variances inter et intra : 6. 12 = 4. 28 + 1. 84. Jeanne Fine http: //finestat. free. fr Statistique descriptive 33

6. TRAITEMENT STATISTIQUE D'UNE VARIABLE RÉELLE ET D'UNE VARIABLE CATÉGORIELLE Formules On note n, et V l'effectif de la population, la moyenne et la variance d'une variable réelle X. On considère une variable catégorielle à K modalités, donc une partition de la population en K classes et on note nk , et Vk l'effectif, la moyenne et la variance de la variable X dans la classe k. On a alors les relations suivantes : et Jeanne Fine http: //finestat. free. fr Statistique descriptive 34

6. TRAITEMENT STATISTIQUE D'UNE VARIABLE RÉELLE ET D'UNE VARIABLE CATÉGORIELLE • Rapport de corrélation entre une variable catégorielle et une variable réelle Le rapport de corrélation entre une variable catégorielle et une variable réelle, noté , est la racine carrée de la variance inter sur la variance totale (= inter + intra) de la variable réelle. Ce rapport est évidemment compris entre 0 et 1. Il est égal à 0 lorsque la variance inter est nulle et il exprime alors l'absence de liaison entre la variable réelle et la variable catégorielle. Il est égal à 1 lorsque la variance inter est égale à la variance totale et il exprime alors une forte liaison entre la variable réelle et la variable catégorielle. Dans l'exemple, la variable réelle MAT 1 et la variable catégorielle GRPE ont pour rapport de corrélation : L'indice est appelé pouvoir discriminant. Jeanne Fine http: //finestat. free. fr Statistique descriptive 35