GRAFURI Chestiuni teoretice Un graf orientat digraf G

GRAFURI Chestiuni teoretice. Un graf orientat (digraf) G este o pereche (V, E), unde C este o multime finita, iar E este o relatie binara pe V. Multimea V se numeste multimea varfurilor lui G, iar elementele ei se numesc varfuri. Multimea E se numeste multimea arcelor lui G, iar elementele ei se numesc arce. Exemplu: a) 1 2 3 4 5 6 1/13/2022 1

V= {1, 2, 3, 4, 5, 6 } E = {(1, 2), (2, 5), (4, 1), (4, 5), (5, 4), (6, 3)} Varfurile sunt reprezentate prin cercuri, iar arcele prin sageti. Autobuclele sunt arce de la un varf la el insusi. Intr-un graf neorientat G = (V, E), multimea muchiilor E este constituita din perechi de varfuri neordonate, si nu din perechi ordonate. O muchie este o multime {u, v} unde u, v V si u v. Prin conventie, pentru o muchie vom folosi notatia (u, v) in locul notatiei pentru multimi {u, v}, iar (u, v) si (v, u) se considera a fi aceeasi muchie. Intr-un graf neorientat, autobuclele sunt interzise si, astfel, fiecare muchie este formata exact din doua varfuri distincte. b) 1 2 3 4 5 6 1/13/2022 2

V= {1, 2, 3, 4, 5, 6 } E = {(1, 2), (2, 5), (3, 6), (1, 5)} Varful 4 este izolat. Multe definitii pentru grafuri orientate si neorientate sunt aceleasi, desi unii termeni pot avea seminificatii diferite in cele doua contexte. Daca (u, v) este un arc intr-un graf orientat G = (V, E), spunem ca (u, v) este incident din sau pleaca din varful u si este incident in sau intra in varful v. De exemplu arcele care pleaca din varful 2 in figura a) sunt (2, 5), (2, 4), (2, 2). Arcele care intra in varful 2 sunt (1, 2), (2, 2). Daca (u, v) este o muchie intr-un graf neorientat G =(V, E) spunem ca (u, v) este incidenta varfurilor u si v. In figura b) muchiile incidente varfului 2 sunt (1, 2) si (2, 5). Daca (u, v) este o muchie (arc) intr-un graf G = (V, E) spunem ca varful v este adiacent varfului u. Daca graful este neorientat, relatia de adiacenta este simetrica. Intr-un graf orientat relatia de adiacenta nu este neaparat simetrica. Daca v este adiacent varfului u intr-un graf oriantat se foloseste notatia u v. In figurile a si b, varful 2 este adiacent varfului 1, deoarece muchia (arcul) (1, 2) ambelor grafuri. Varful 1 nu este adiacent varfului 2 in fig. a, deoarece muchia (2, 1) nu apartine grafului. Gradul unui varf al unui graf neorientat este numarul de muchii incidente acestuia. De exemplu, varful 2 din fig. b are gradul 2. Un varf al carui gard este 0 se numeste varf izolat (ex. varful 4). Intr-un graf orientat, gradul exterior al unui varf este numarul arcelor ce pleaca din el, iar gradul interior al unui varf este numarul arcelor ce intra in el. Gradul unui varf al unui graf orientat este gradul sau exterior plus gradul sau interior. Varful 2 din fig. a are gradul interior 2 gradul exterior 3 si gradul 2+3=5. Un drum de lungime k de la un varf u’ intr-un graf G=(V, E) este un sir de varfuri <V 0, v 1, . . . Vk> astfel incat u=v 0, u”=vk si (vi-1, vi) E pentru i=1, 2, . . . k. 1/13/2022 3

Lungimea unui drum este numarul de muchii (arce) din acel drum. Drumul contine varfurile v 0, v 1, v 2. . . vk si muchiile (v 0, v 1), (v 1, v 2), . . . (vk-1, vk). Daca exista un drum p de la u’spunem ca u’este accesibil din u prin p, relatie reprezentata si prin u=>u’ daca G este orientat. Un drum este elementar daca toate varfurile din el sunt distincte. Ex. in fig. a drumul <1, 2, 5, 4> este un drum elementar de lungime 3. Drumul <2, 5, 4, 5, > nu este elementar. Un subdrum al unui drum p = <v 0, v 1, . . . vk> este un subsir continuu al varfurilor sale. Pentru orice 0 i j k, subsirul de varfuri <vi, vi+1, . . . , vj> este un subdrum al lui p. Intr-un graf orientat, un drum <v 0, v 1. . . vk> formeaza un ciclu daca v 0 = vk si drumul contine cel putin o u’ muchie. Ciclul ueste elementar daca v 1, v 2. . . vk sunt distincte. O autobucla este un ciclu de lungime 1. Doua drumuri < v 0, v 1, v 2, . . . vk-1, v 0> si < v 0’, v 1’, v 2’, . . . v’k-1, v 0’> formeaza acelasi ciclu daca exista un intreg j astfel incat vi = V(i+j) mod K pentru i=0, 1, . . k-1. Ex. in fug. a drumul <1, 2, 4, 1> formeaza acelasi ciclu ca drumurile <2, 4, 1, 2> si <4, 1, 2, 4>. Acest ciclu este elementar. Ciclul <1, 2, 4, 5, 4, 1> nu este elementar. Ciclul <2, 2> fomat din muchia (2. 2) este o autobucla. Un graf orientat fara autobucle este elementar. Intr-un graf neorientat un drum <v 0, v 1, . . . vk> formeaza un ciclu elementar daca k>3, v 0=vk si varfurile v 1, v 2. . . vk sunt distincte. De exemplu in fig. b drumul <1, 2, 5, 1> este un ciclu elementar. Un graf fara cicluri este acidic. Un graf neorientat este conex daca fiecare pereche de varfuri este conectata printr-un drum. Componenetele conexe ale unui graf sunt clasele de echivalenta ale varfurilor sub relatia “este accesibil din”. Graful b are 3 componente conexe: {1, 2, 5}, {3, 6}, {4}. Fiecare varf din {1, 2, 5} este accesibil din fiecare varf din {1, 2, 5}. 1/13/2022 4

Un graf neorientat este conex daca are exact o componenta conexa, sau, altfel spus, daca fiecare varf este accesibil din fiecare varf diferit de el. Un graf orientat este tare conex daca fiecare doua varfuri sunt accesibile din celalalt. Componenetele tare conexe ale unui graf sunt clasele de echivalenta ale varfurilor sub relatia “sunt reciproc accesibile”. Un graf orientat este tare conex daca are doar o singura componenta tare conexa. Graful din fig. a are 3 componente tare conexe: {1, 2, 4, 5} , {3} si [6}. Toate perechile de varfuri din {1, 2, 4, 5} sunt reciproc accesibile. Varfurile [3, 6} nu formeaza o componenta tare conexa, deoarece varful 6 nu este accesibil din varful 3. Doua grafuri G= (V, E) si G’=(V’, E’) sunt izomorfe daca exista o bijectie f: V V’astfel incat (u, v) E daca si numai daca (f(u), f(v)) E’. Cu alte cuvinte, pentru a reeticheta varfurile lui G pentru ca acestea sa fie varfuri din G’, pastrand muchiile corespunzatoare din G si G’. Figura aa prezinta o pereche de grafuri G si G’cu multimile de varfuri V={1, 2, 3, 4, 5, 6} si V’={u, v, w, x, y, z}. Functia din V’, data de f(1) = u, f(2) = v, f(3) = w, f(4) = x, f(5) = y, f(6) = z este functia bijectiva ceruta. Grafurile din fig. bb nu sunt izomorfe. Desi ambele grafuri au 5 varfuri si 7 muchii, graful din partea superioara are varf cu gradul egal 4, in timp ce graful din partea inferioara a figurii nu poseda un astfel de varf. 1/13/2022 5

Fig. aa G G’ 2 1 6 3 5 v u w x y z 4 Fig. bb 1 2 u 5 v w x y 3 4 1/13/2022 6

Spunem ca un graf G’= (V’, E’) este un subgraf al grafului G =(V, E) daca V’= V si E’. Daca fiind o multime V’ V, subgraful lui G indus de V’este graful G’= (V’, E’) unde E’= {(u, v) E : u, v V’} Subgraful indus de multimea de varfuri [1, 2, 3, 6} din fig. a apare in fig. c 3 1 2 6 si are multimea de muchii {(1, 2), (2, 2), (6, 3)} Fiind dat un garf neorientat G = (V, E), versiunea orientat alui G este graful orientat G’(V, E’) unde (u, v) E’ daca si numai daca (u, v) E. Adica fiecare muchie neorientata (u, v) din G este inlocuita in versiunea orientat prin doua arce orientate (u, v) si (v, u). Invers pentru un graf orientat G = (V, E), versiunea neorientata a lui G este graful neorientat G’= (V, E’) unde (u, v) E’daca si numai daca u v si (u, v) E. Versiunea neorienta contine arcele lui G “cu directiile eliminate”si cu autobuclele eliminate. Deoarece (u, v) si (v, u) reprezinta aceeasi muchie intr-un graf neorientat, versiunea neorientata a unui graf orientat o contine o singura data, chiar daca graful orintat contine atat muchia (w, v) cat si muchia (v, u). Intr-un graf orientat G = (V. E), un vecin al unui varf u este orice varf care este adiacent lui u in versiunea neorientata a lui G. deci v este vecin a lui u daca (u, v) E sau (v, u) E. Intr-un graf neorientat, u si v sunt vecine daca sunt adiacente. 1/13/2022 7

Un graf complet este un graf neorientat in care oricare doua varfuri sunt adiacente. Un graf bipartit este un graf neorientat G = (V, E) in care multimea V poate fi partitionata in 2 multimi V 1 si V 2 astfel incat (u, v) E implica fie ca u V 1 si v V 2, fie ca u V 2 si v V 1, adica muchiile merg de la multimea V 1 la multimea V 2 sau invers. Un graf neorientat, aciclic este o padure, iar un graf neorientat, aciclic si conex este un arbore (liber). Reprezentarea grafurilor Exista doua moduri standard de reprezentare a unui graf G = (V, E): ca o multime de lista de adiacenta sau ca o matrice de adiacenta Reprezentarea prin liste de adiacenta este preferata pentru ca ofera un mod compact de reprezentare a grafurilor rare acelea pentru care |E| numarul de muchii (arce) – gradul –este mult mai mic decat |V| 2 (patratul numarului de varfuri). Reprezentarea prin matrice de adiacenta este preferata atunci cand graful este dens, adica |E| este aproximativ egal cu |V|2 – sau atunci cand trebuie sa decidem, rapid, daca exista o muchie ce conecteaza doua varfuri date. Reprezentarea prin liste de adiacenta a unui graf G = (V, E) consta dintr-un tablou Adj cu |V| liste, una pentru fiecare varf din V. Pentru fiecare u V, lista de adiacenta Adj [u] contine pointeri la toate varfurile v pentru care exista o muchie (u, v) E. Lista Adj [u] este formata din totalitatea varfurilor adiacente lui u in G. Varfurile din fiecare lista de adiacenta sunt memorate intr-o ordine arbitrara. 1/13/2022 8

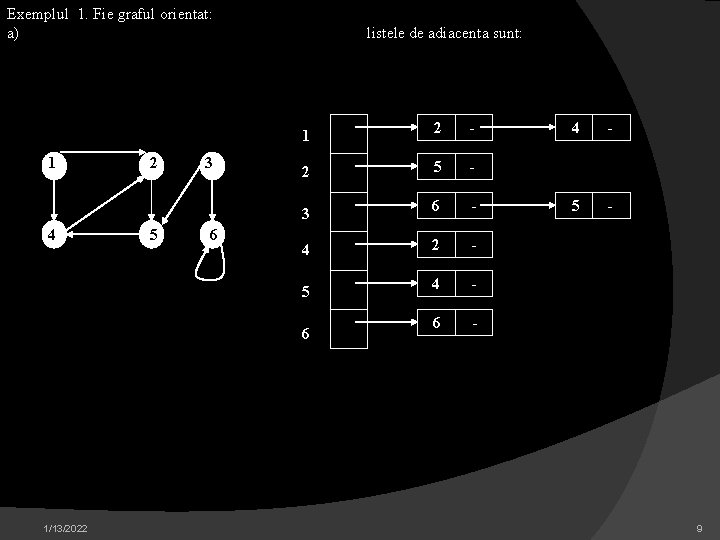
Exemplul 1. Fie graful orientat: a) 1 4 2 5 3 6 listele de adiacenta sunt: 1 2 - 2 5 - 3 6 - 4 2 - 5 4 - 6 1/13/2022 4 - 5 - 9

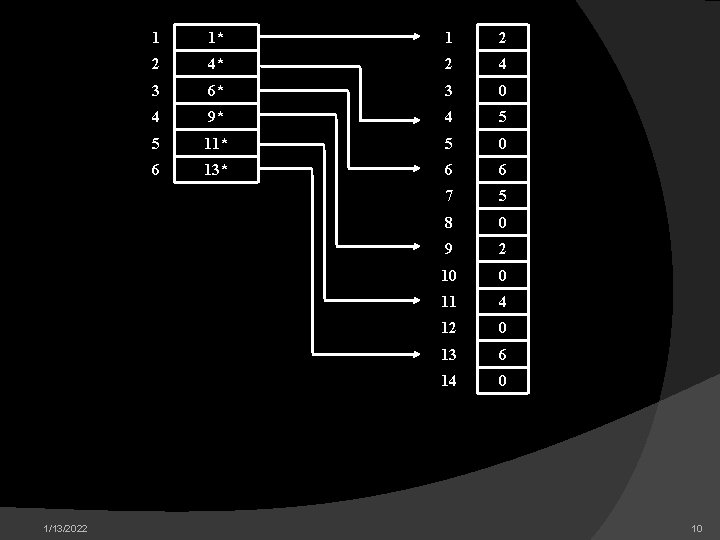
1/13/2022 1 1* 1 2 2 4* 2 4 3 6* 3 0 4 9* 4 5 5 11* 5 0 6 13* 6 6 7 5 8 0 9 2 10 0 11 4 12 0 13 6 14 0 10

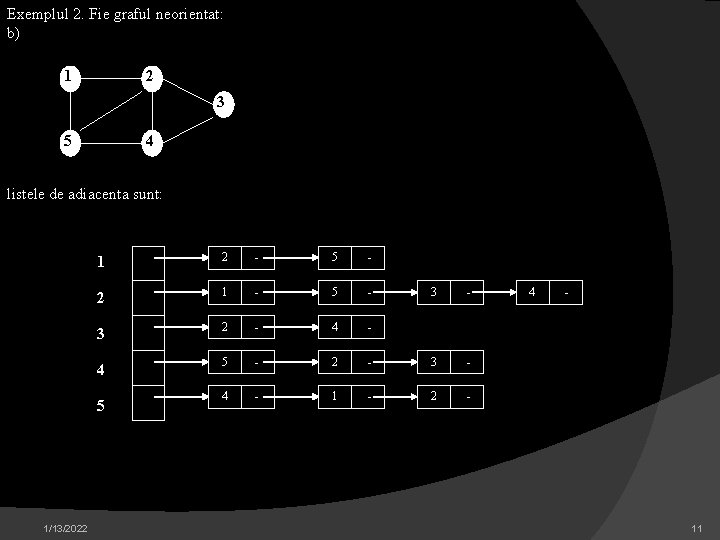
Exemplul 2. Fie graful neorientat: b) 1 2 3 5 4 listele de adiacenta sunt: 1 2 - 5 - 2 1 - 5 - 3 2 - 4 5 - 2 4 - 1 5 1/13/2022 3 - - 2 - 4 - 11

Daca G este un graf orientat, suma lungimilor tuturor listelor de adiacenta este |E|, deoarece un arc de forma (u, v) este reprezentat prin aparitia lui v in Adj(u). Daca G este un graf neorientat, suma lungimilor tuturor listelor de adiacenta este 2*|E|, deoarece, daca (u, v) este o muchie, atunci n apare in lista de adiacenta a lui v si invers. Indiferent daca un graf este orientat sau nu, reprezentarea prin lista de adiacenta are proprietatea dezirabila ca dimensiunea memoriei necesare este O(max(V, E)) = O(V, E). Listele de adiacenta pot fi usor adaptate pentru reprezentarea grafurilor cu costuri (ponderate), adica acele grafuri in care fiecarei muchii i s-a asociat un cost dat, de obicei, de o functie de cost w: E R. De exemplu, die G = (V, E) un graf cu costuri avand functia de cost w. Costul w(u, v) al muchiei (u, v) E este memorat pur si simplu impreuna cu varful v in lista de adiacenta a lui u. Reprezentarea prin liste de adiacenta este foarte robusta in sensul ca poate fi modificata pentru a suporta multe alte variante de grafuri. Un dezavantaj al reprezentarii prin liste de adiacenta este acela ca nu exista alta cale mai rapida determina daca o muchie (u, v) apartine grafului, decat cautarea lui v in lista de adiacenta a lui u, Adj[u]. Dezavantajul acesta poate fi remediat folosind o reprezentare a grafului prin matrice de adiacenta, dar solicitand mai multa memorie. Pentru a reprezenta un graf G = (V, E) prin matrice de adiacenta presupunem ca varfurile u V sunt numerotate in mod arbitrar cu 1, 2, . . . |V|. reprezentarea consta intr-o matrice A = (aij) de dimensiune |V| x |V| astfel incat: aij = 1/13/2022 12

Matricele de adiacenta ale grafurilor a si b sunt: 1 2 3 4 5 6 1 0 0 0 2 1 0 0 3 0 0 0 4 5 1 0 0 0 graf orientat 1/13/2022 6 0 0 1 1 1 0 2 1 3 0 2 1 0 1 3 0 1 0 4 0 1 1 5 1 1 0 4 0 1 1 0 1 5 1 1 0 graf orientat – matrice simetrica 13

Necesarul de memorie pentru matricea de adiacenta este (V 2) si nu depinde de numarul de muchii ale grafului. Deoarece intr-un graf neorientat (u, v) si (v, u) reprezinta aceeasi muchie, matricea de adiacenta A este propria sa transpusa A = At. In anumite aplicatii este avantajos sa stocam (memoram) numai elementele situate pe si deasupra diagramei principale, reducand necesarul de memorie la jumatate. La fel ca la reprezentarea prin liste de adiacenta, la reprezentarea prin matrice de adiacenta, acesta poate fi folosita si pentru grafuri cu cost (ponderate). Daca G = (V, E) este un graf cu cost, avand costul unei muchii dat de functia w, costul w(u, v) al muchiei (u, v) E este memorat pur si simplu ca un element in linia u si coloana v a matricei de adiacenta. Daca o muchie nu exista, elementul corespunzator poate fi NULL, NIL, 0 sau . Simplitatea matricei de adiacenta o face preferabila, atunci cand graful are un numar relativ mic de noduri, daca graful este fara costuri, avantajul reprezentarii prin matrice de adiacenta este reprezentarea fiecarui element al acestuia pe cate un bit. Folosind pentru reprezentarea grafurilor listele de adiacenta ultima varianta descrierea structurilor de date si a functiilor de acces si de initializare aaferente se dau mai jos. Modulul comune. h contine definitiile unor constante simbolice si macroinstructiunile referitoare la tratarea erorilor. Modulul graf. h contine declaratiile structurilor de date si functiile referitoare la grafuri. Definitiile acestora sunt date in modulul graf. c 1/13/2022 14

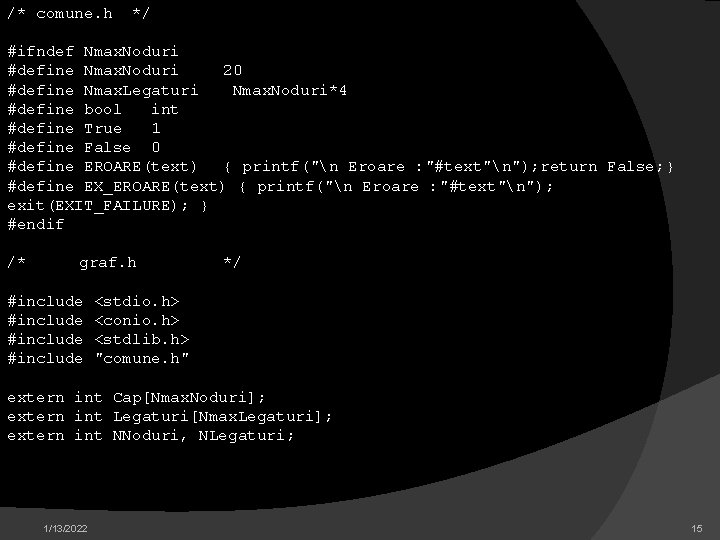
/* comune. h */ #ifndef Nmax. Noduri #define Nmax. Noduri 20 #define Nmax. Legaturi Nmax. Noduri*4 #define bool int #define True 1 #define False 0 #define EROARE(text) { printf("n Eroare : "#text"n"); return False; } #define EX_EROARE(text) { printf("n Eroare : "#text"n"); exit(EXIT_FAILURE); } #endif /* graf. h #include */ <stdio. h> <conio. h> <stdlib. h> "comune. h" extern int Cap[Nmax. Noduri]; extern int Legaturi[Nmax. Legaturi]; extern int NNoduri, NLegaturi; 1/13/2022 15

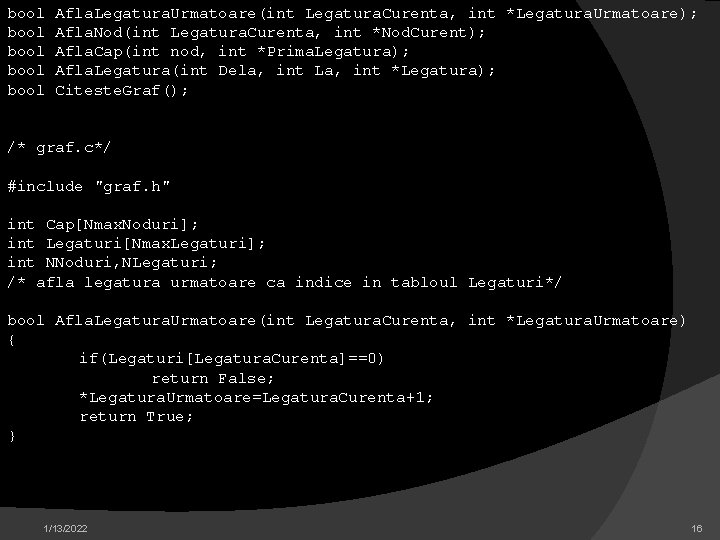
bool bool Afla. Legatura. Urmatoare(int Legatura. Curenta, int *Legatura. Urmatoare); Afla. Nod(int Legatura. Curenta, int *Nod. Curent); Afla. Cap(int nod, int *Prima. Legatura); Afla. Legatura(int Dela, int La, int *Legatura); Citeste. Graf(); /* graf. c*/ #include "graf. h" int Cap[Nmax. Noduri]; int Legaturi[Nmax. Legaturi]; int NNoduri, NLegaturi; /* afla legatura urmatoare ca indice in tabloul Legaturi*/ bool Afla. Legatura. Urmatoare(int Legatura. Curenta, int *Legatura. Urmatoare) { if(Legaturi[Legatura. Curenta]==0) return False; *Legatura. Urmatoare=Legatura. Curenta+1; return True; } 1/13/2022 16

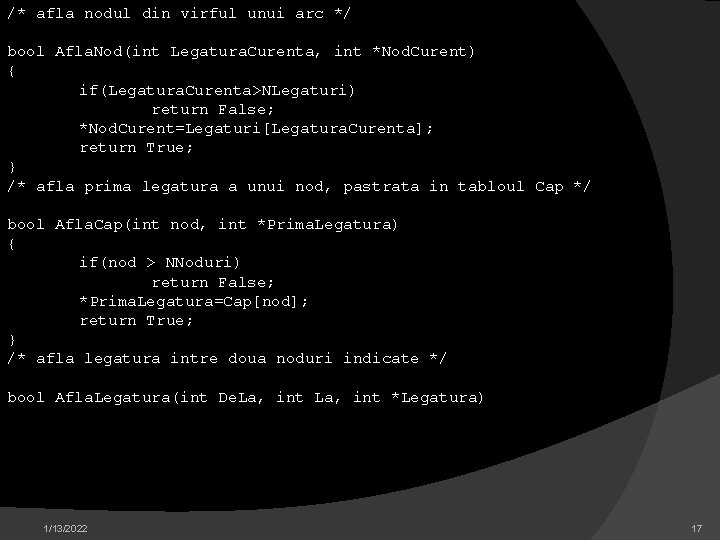
/* afla nodul din virful unui arc */ bool Afla. Nod(int Legatura. Curenta, int *Nod. Curent) { if(Legatura. Curenta>NLegaturi) return False; *Nod. Curent=Legaturi[Legatura. Curenta]; return True; } /* afla prima legatura a unui nod, pastrata in tabloul Cap */ bool Afla. Cap(int nod, int *Prima. Legatura) { if(nod > NNoduri) return False; *Prima. Legatura=Cap[nod]; return True; } /* afla legatura intre doua noduri indicate */ bool Afla. Legatura(int De. La, int *Legatura) 1/13/2022 17

{ int i; if(De. La > NNoduri||La > NNoduri) return False; /*depasire numar curent de noduri*/ i=Cap[De. La]; while(Legaturi[i] != La && Legaturi[i] != 0) i++; *Legatura=i; if(Legaturi[i]==0) *Legatura=0; return True; } /* initiaza graful/ Actualizeaza tabl Cap si Legaturi conform cu graful propus de utilizator/ rezultatul este False daca se depaseste numarul maxim de legaturi/ True daca initializarea se face corect*/ bool Citeste. Graf() { int n, i, j, Legatura. Curenta; do{ printf("n numar noduri(<=%d): ", Nmax. Noduri); scanf("%d", &NNoduri); } while (NNoduri> Nmax. Noduri); 1/13/2022 18

Legatura. Curenta=1; for(i=1; i<=NNoduri; i++){ Cap[i]=Legatura. Curenta; printf("dati nodurile adiacnt lui %d; 0 pentru terminaren", i); do { do{ printf("nod"); scanf("%d", &j); } while(j>NNoduri); Legaturi[Legatura. Curenta++]=j; }while(j!=0 && Legatura. Curenta<Nmax. Legaturi); if(Legatura. Curenta==Nmax. Legaturi&&j!=0) return False; } NLegaturi=Legatura. Curenta; return True; } 1/13/2022 19

Metode de cautare intr-un graf Cautarea intr-un graf inseamna parcurgerea, in mod sistematic, a muchiilor grafului astfel incat sa parcurgem varfurile grafului. Un algoritm de cautare intr-un graf poate descoperi multe informatii despre structura grafului respectiv. Astfel unii algoritmii de grafuri incep prin a cauta in graful de intrare pentru a obtine aceasta informatie structurala, iar acesti algoritmi sunt simple rafinari ale unor algoritmi de cautare de baza. Cautare in latime (Algoritmul BF breadth first) Fie ungraf G = (V<E) si un nod sursa s, cautarea (parcurgerea) in latime exploreaza sistematic muchiile lui G pentru a “descoperi” fiecare nod care este accesibil lui s. Algoritmul calculeaza distanta (cel mai mic numar de muchii) de la s la toate varfurile accesibile. El produce un “arbore de latime” cu radacina s, care contine toate aceste varfuri accesibile. Pentru fiecare varf v accesibil din s, calea din arborele de latime de la s la v corespunde unui “cel mai scurt drum”de la s la v in G, adica un drum care contine un numar minim de muchii. Algoritmul functioneaza atat pe grafuri orientate cat si pe grafui neorientate. Parcurgerea in latime este numita astfel pentru ca largeste, uniform, frontiera dintre nodurile descoperite si cele nedescoperite, pe latimea frontierei. Aceasta inseamna ca algoritmul descopera toate varfurile aflate la distanta k fata de s inainte de a desoperi vreun varf la distanta k+1. Exemplu. Fie graful neorientat si s=1, arborele de latime arata astfel: 1/13/2022 20

1 2 4 1 3 5 2 6 7 3 5 4 6 8 8 7 Ordinea de parcurgere este urmatoarea: 1, 2, 3, 4, 5, 6, 7, 8 Adica este vizitata radacina “culoarului de latime” , apoi sunt vizitate varfurile de pe nuvelul 1, apoi cele de pe nivelul 2 s. a. m. d. Pentru a tine evidenta nodurilor parcurse, cautare in latime se “coloreaza” fiecare nod cu alb, gri sau negru. Pentru inceput toate varfurile sunt colorate la inceput in alb si pot deveni apoi gri sau negru. Un varf este decoperit cand este intalnit prima data in timpul unei cautari, moment in care nu mai este alb. De aceea varfurile gri si negru sunt descoperite, dar algoritmul face distinctie intre ele pentru a fi sigur ca procesul de cautare loc pe latime. Daca (u, v) E si varful u este negru, atunci varful v aste sau gri sau negru, adica toate varfurile adiacente unui nod negru au fost descoperite. Varfurile gri pot avea varfuri adiacente albe. Acestea reprezinta frontiera intre varfurile descoperite si cele nedescoperite. 1/13/2022 21

Algoritmul de parcurgere (cautare) in latime construieste un arbore de latime ce contine, initial, numai radacina sa care este varful s. De cate ori un varf alb v este descoperit in cursul parcurgerii listei de adiacenta a unui varf u deja descoperit, virful v si muchia (u, v) sunt adaugate in arbore. In acest caz, spunem ca u este predecesorul sau parintele lui v in arborele de latime. Deoarece un varf este descoperit cel mult o data, el poate avea cel mult un parinte. Relatiile de stramos si descendent, din arborele de latime, sunt definite relativ la radacina s in mod obisnuit: daca u se afla pe un drum din arbore de la radacina s la varful v, atunci u este un stramos al lui v, iar v este un descendent al lui u. Procedura de cautare in latime BF – presupune ca graful G = (V, E) este reprezentat folosind liste de adiacenta. Algoritmul foloseste mai multe structuri de date pentru fiecare varf din graf. Culoarea fiecarui varf u V este memorata in variabila culoare (u), iar predecesorul lui u este memorat in variabila P(u). Daca u nu are nici un predecesor (de ex. daca u=s sau u nu a fost descoperit) atunci P(u) = NULL. Distanta de la sursa s la varful u, calculata de algoritm, este memorata in d(u). In algoritm se foloseste o coada, Q de tipul primul sosit, primul venit, FIFO, pentru a prelucra multimea de varfuri gri. Algoritmul BF 1/13/2022 22

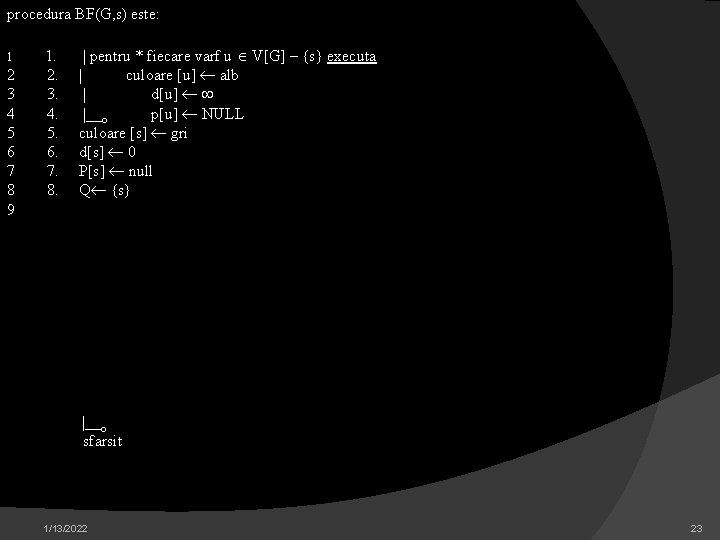
procedura BF(G, s) este: 1 2 3 4 5 6 7 8 9 1. 2. 3. 4. 5. 6. 7. 8. | pentru * fiecare varf u V[G] – {s} executa | culoare [u] alb | d[u] |__o p[u] NULL culoare [s] gri d[s] 0 P[s] null Q {s} |__o sfarsit 1/13/2022 23

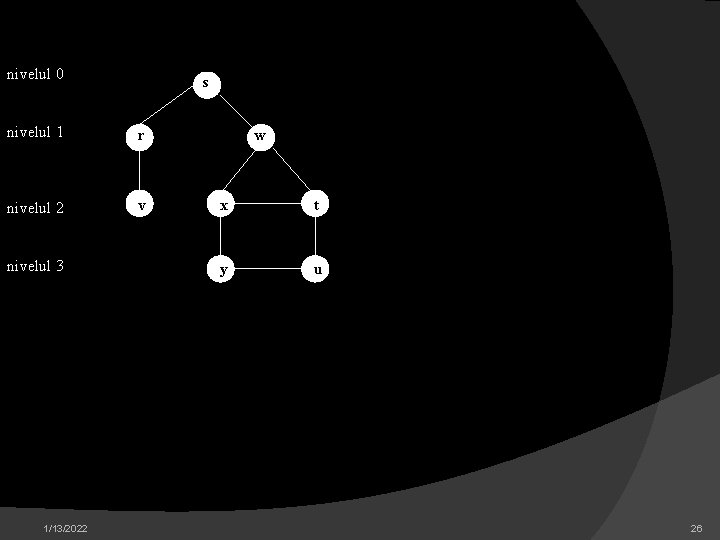
9 | cat timp Q 0 executa 10. | u cap [Q] 11 | pentru *fiecare varf v Adj[u] executa 12 | | daca culoare [v] = alb atunci 13 | | culoare [v] gri 14 | | d[v] d[u] +1 15 | | p[u] u 16 | |__o * pune in coada (Q, v) // Q Q + v 17 | scoate din coada (Q) 18 | color [u] negru sfarsit 1/13/2022 24

Procedura BF() opereaza astfel: liniile 1 – 4 coloreaza toate varfurile in alb, atribuie lui [u] valoarea pentru fiecare varf u si seteaza parintele fiecarui varf pe NULL. Linia 5 coloreza varful sursa s in gri, deoarece el este considerat descoperit atunci cand se intra in procedura. Linia 6 initializeaza d[s] cu 0, iar linia 7 initializeaza predecesorul sursei cu NULL. Linia 8 initializeaza COADA Q cu s (Q contine multimea varfurilor gri). Bucla principala a programului este continuta in liniile 9 – 18. Iteratia are loc cat timp mai exista varfuri gri, adica varfuri descoperite a caror lista de adiacenta nu a fost examinata in intregime. Linia 10 determina varful gri u din capul cozii Q. Bucla pentru din liniile 11 16 , considera fiecare varf v din lista de adiacenta lui u. Daca v este alb, atunci el nu a fost inca descoperit si algoritmul il descopera executand liniile 13 – 16. La inceput, el este colorat cu gri, iar distanta d[v] este initializata cu d[u] + 1. Apoi, u este inregistrat ca parinte al sau. In final, varful v este plasat la sfarsitul cozii Q. Cand toate varfurile din lista de adiacenta a lui u au fost examinate, u este scos din coada Q si colorat in negru in liniile 17 – 18. Exemplu: Fie graful neorientat: r s t u v w x y si varful sursa (initial) s. “Arborele de latime” va fi: 1/13/2022 25

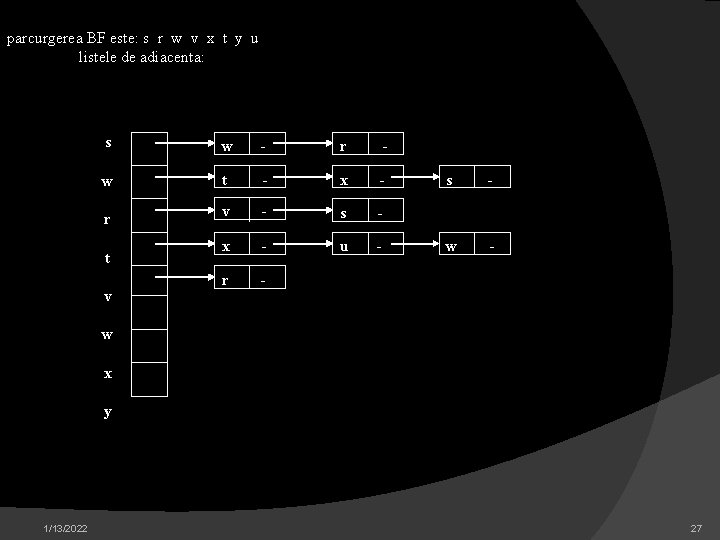
nivelul 0 s nivelul 1 r nivelul 2 v nivelul 3 1/13/2022 w x t y u 26

parcurgerea BF este: s r w v x t y u listele de adiacenta: s w - r - w t - x - v - s - x - u - r t v s - w x y 1/13/2022 27

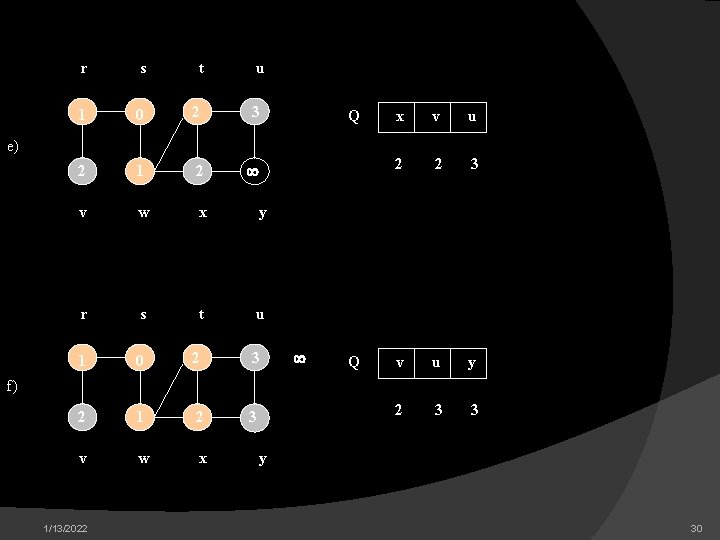
Executia algorimului BF pe acest graf neorientat urmeaza. Muchiile arborelui sunt prezentate hasurat (dublate) asa cun sunt produse de BF. Impreuna cu fiecare varf u, este prezentata si d[u]. Coada Q este prezentata la inceputul fiecarei iteratii a buclei cat timp din liniile 9 – 18. Distantele varfurilor sunt prezentate langa varfurile din coada. a) r s b) t 0 v w x 1/13/2022 r s t s 1 0 0 1 v w x u Q y u Q W r 1 1 y 28

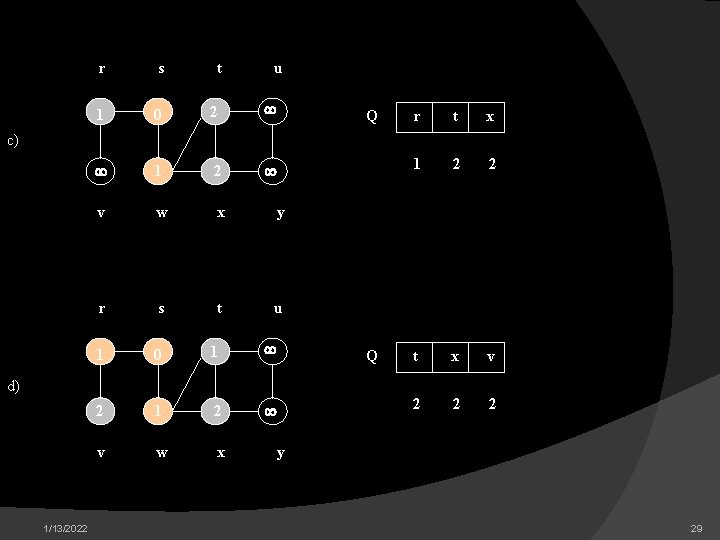
r s t u 1 0 2 1 2 v w x y r s t u 1 0 1 2 v w x Q r t x 1 2 2 t x v 2 2 2 c) Q d) 1/13/2022 y 29

r s t u 1 0 2 3 2 1 2 v w x y r s t u 1 0 2 3 2 1 2 3 v w x Q x v u 2 2 3 v u y 2 3 3 e) Q f) 1/13/2022 y 30

r s t u 1 0 2 1 2 3 v w x u y g) 3 3 y h) i) r s t u 1 0 2 3 2 1 2 3 v w x 1/13/2022 y Q r s t y 1 0 3 2 1 2 v w x 2 u 3 Q 0 3 y 31

In concluzie cautarea in largime continua intotdeauna cu primul nod vizitat care mai are arce neexplorate. Pentru aceasta se foloseste o coada Q in care se inscriu nodurile in ordinea in care sunt intilnite: nodul initial s, apoi nodurile r, w, …adiacente lui s, apoi cele adiacente lui w etc. Un pseudocod al acestui tip de cautare: Exporare. In. Largime(s) este Explorate<-{s} *prelucreaza informatia din s *introdu s in coada Q |cat timp Q<> coada_vida executa | v<- primul nod din coada Q | |pentru *fiecare nod w adiacent lui v executa | | | daca w nu apartine lui Explorate atunci | | | *adauga w la Explorate | | | *prelucreaza informatia din w | | | *introdu w in coada Q | | | Pentru implementare se fac urmatoarele precizari: Se implementeaza coada printr-un tablou de intregi si nu ca o structura dinamica. Aceasta solutie este rigida si ineficienta, fiind aleasa pe motivul simplitatii descrierii. Functiile de acces si de modificare utilizate sunt similare celor din cazul general. 1/13/2022 32

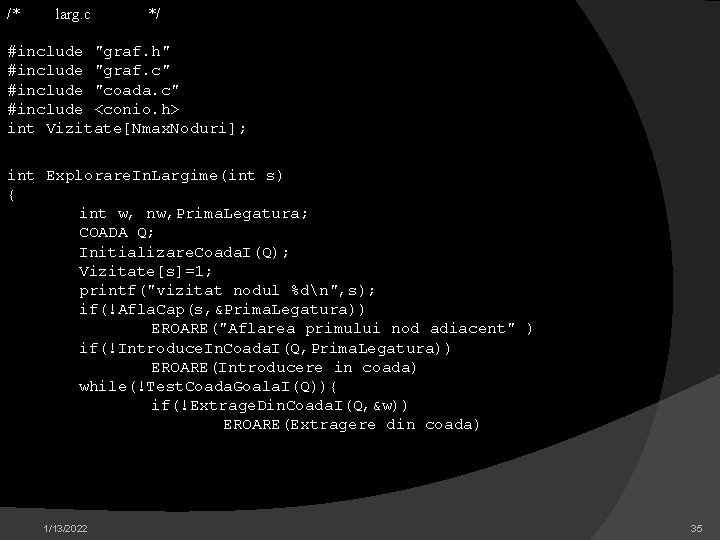
/* coada. h */ #include "comune. h" typedef int COADA[Nmax. Legaturi]; bool Initializare. Coada. I(COADA Q); // initializeaza structura rezervata Q bool Introduce. In. Coada. I(COADA Q, int e); // introduce un element nou la sfirsitul cozii bool Extrage. Din. Coada. I(COADA Q, int *pe); //extrage elementul de la inceputul cozii Test. Coada. Goala. I(COADA daca exista elemente in coada Q -bool - multimea vizitata este implementata. Q); //testeaza ca un tablou. - - se foloseste stilul programarii defensive cu captarea tuturor erorilor posibile - - se face parcurgerea tuturor nodurilor grafului. Prelucrarea fiecarui nod consta doar in afisarea etichetelor sale /* coada. c #include "coada. h" */ int Nr. Elem; bool Initializare. Coada. I(COADA Q){ Nr. Elem=0; return True; } 1/13/2022 33

bool Introduce. In. Coada. I(COADA Q, int e){ if (Nr. Elem<Nmax. Legaturi){ Q[Nr. Elem]=e; Nr. Elem++; return True; } return False; } bool Extrage. Din. Coada. I(COADA Q, int *pe){ int i; if (Nr. Elem>0){ *pe=Q[0]; for (i=0; i<Nr. Elem-1; i++){ Q[i]=Q[i+1]; } Nr. Elem--; return True; } return False; } bool Test. Coada. Goala. I(COADA Q){ if (Nr. Elem==0) return True; return False; } 1/13/2022 34

/* larg. c */ #include "graf. h" #include "graf. c" #include "coada. c" #include <conio. h> int Vizitate[Nmax. Noduri]; int Explorare. In. Largime(int s) { int w, nw, Prima. Legatura; COADA Q; Initializare. Coada. I(Q); Vizitate[s]=1; printf("vizitat nodul %dn", s); if(!Afla. Cap(s, &Prima. Legatura)) EROARE("Aflarea primului nod adiacent" ) if(!Introduce. In. Coada. I(Q, Prima. Legatura)) EROARE(Introducere in coada) while(!Test. Coada. Goala. I(Q)){ if(!Extrage. Din. Coada. I(Q, &w)) EROARE(Extragere din coada) 1/13/2022 35

while(Afla. Nod(w, &nw) && (nw!=0)){ if(Vizitate[nw]==0){ Vizitate[nw]=1; printf("vizitat nodul %dn", nw); if(!Afla. Cap(nw, &Prima. Legatura)) EROARE(Aflare nod adiacent) if(!Introduce. In. Coada. I(Q, Prima. Legatura)) EROARE(introducere in coada) } if(!Afla. Legatura. Urmatoare(w, &w)) EROARE(Aflare legatura urmatoare) } } return True; } bool main() { 1/13/2022 36

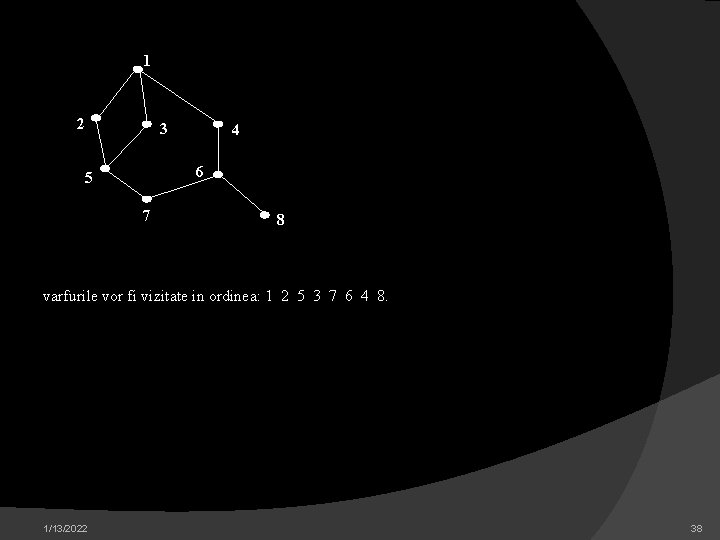
int start; clrscr(); Citeste. Graf(); for(start=1; start<NNoduri; start++) Vizitate[start]=0; for(start=1; start<NNoduri; start++) if(Vizitate[start]==0){ printf("n Exporare din %dn", start); if(!Explorare. In. Largime(start)) exit(EXIT_FAILURE); } printf("n sfirsit explorare"); exit(EXIT_SUCCESS); return; } Cautarea in adincime DF(depth first) Algoritmul DF (depth first) se deosebeste de algoritmul BF (breadth first) prin aceea ca explorarea continua intotdeauna cu ultimul nod vizitat care mai are arce neexplorate. Pentru a realiza acest lucru se foloseste o stiva in care se inscriu nodurile in ordinea in care sunt intilnite: nodul initial 1 apoi primul nod 2 adiacent lui 1, apoi primul nod adiacent lui 2 etc. De fiecare data se exploreaza urmatoarea legatura a nodului din varful stivei, nodul fiind eliminat din stiva cand sunt vizitate toate nodurile adiacente lui. Pentru graful 1/13/2022 37

1 2 3 4 6 5 7 8 varfurile vor fi vizitate in ordinea: 1 2 5 3 7 6 4 8. 1/13/2022 38

Algoritmul in pseudocod este: Exporare. In. Adincime(s) este Vizitate<-{s} *prelucreaza informatia din s *introdu s in stiva S |cat timp S<> stiva_vida executa | v<- varf stiva S | w<- urmatorul nod adiacent lui v | | | daca nu exista w atunci | | | *scoate v din stiva | | |altfel | || | daca w nu apartine lui Vizitate atunci | | | *aduaga w la Vizitate | | | *prelucreaza informatia din w | | | *introdu w in stiva S | | | - 1/13/2022 39

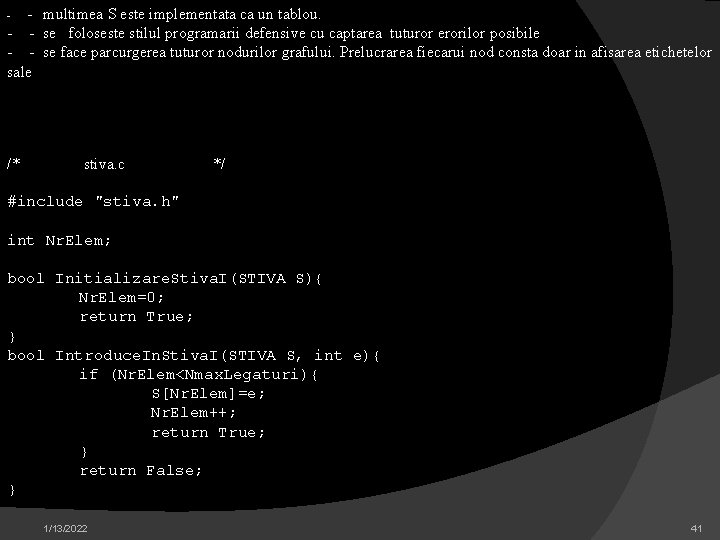
Pentru implementare se fac urmatoarele precizari: -Se implementeaza stiva printr-un tablou de intregi si nu ca o structura dinamica. Aceasta solutie este rigida si ineficienta, fiid aleasa pe motivul simplitatii descrierii. Functiile de acces si de modificare utilizate sunt similare celor din cazul general. - multimea S este implementata ca un tablou. - se foloseste stilul programarii defensive cu captarea tuturor erorilor posibile - se face parcurgerea tuturor nodurilor grafului. Prelucrarea fiecarui nod consta doar in afisarea etichetelor sale /* stiva. h */ #include "comune. h" typedef int STIVA[Nmax. Noduri]; bool Initializare. Stiva. I (STIVA S); /* initializeaza o stuctura rezervata */ bool Introduce. In. Stiva. I (STIVA S, int e); /* introduce un element in stiva */ bool Extrage. Din. Stiva. I (STIVA S, int* pe); /* extrage un element din stiva */ bool Test. Stiva. Goala. I (STIVA S); /* testeaza daca sunt elemente in stiva */ bool Valoare. Din. Varf. I (STIVA S, int* pe); /* afla valoarea din varful stivei */ 1/13/2022 40

- multimea S este implementata ca un tablou. - - se foloseste stilul programarii defensive cu captarea tuturor erorilor posibile - - se face parcurgerea tuturor nodurilor grafului. Prelucrarea fiecarui nod consta doar in afisarea etichetelor sale - /* stiva. c */ #include "stiva. h" int Nr. Elem; bool Initializare. Stiva. I(STIVA S){ Nr. Elem=0; return True; } bool Introduce. In. Stiva. I(STIVA S, int e){ if (Nr. Elem<Nmax. Legaturi){ S[Nr. Elem]=e; Nr. Elem++; return True; } return False; } 1/13/2022 41

bool Extrage. Din. Stiva. I(STIVA S, int *pe){ if (Nr. Elem>0){ *pe=S[Nr. Elem-1]; Nr. Elem--; return True; } return False; } bool Test. Stiva. Goala. I(STIVA S){ if (Nr. Elem==0) return True; return False; } bool Valoare. Din. Varf. I(STIVA S, int *pe){ if (Nr. Elem>0){ *pe=S[Nr. Elem-1]; return True; } return False; } 1/13/2022 42

Parcurgerea in adincime: #include "graf. c" #include "stiva. c" #include <conio. h> int Vizitate [Nmax. Noduri]; bool Explorare. In. Adancime (int s){ int j, v, w, nw, Prima. Legatura; STIVA S; Initializare. Stiva. I(S); Vizitate[s] = 1; printf("vizitat nodul %dn", s); if (!Afla. Cap(s, &Prima. Legatura)) EROARE("Aflare prima legatura"); if (!Introduce. In. Stiva. I(S, Prima. Legatura)) EROARE("Introducere in stiva"); while (! Test. Stiva. Goala. I(S)){ if (!Extrage. Din. Stiva. I(S, &w)) EROARE("Extragere din stiva"); if (!Afla. Nod(w, &nw)) EROARE("Aflare nod"); if (nw!=0){ 1/13/2022 43

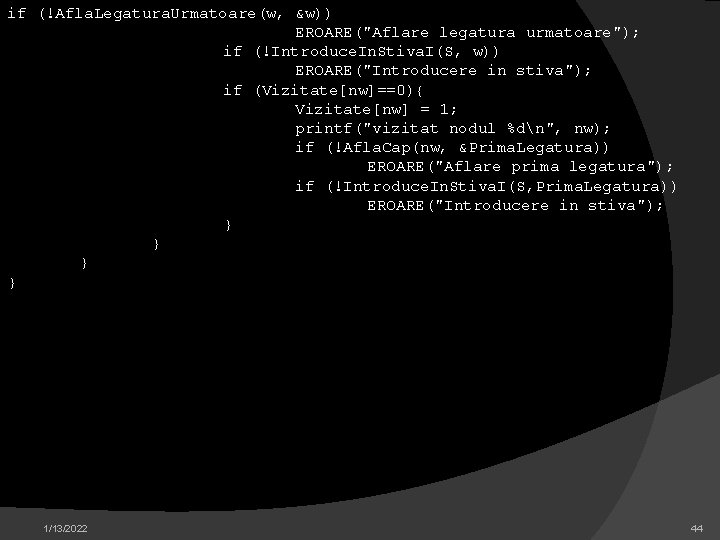
if (!Afla. Legatura. Urmatoare(w, &w)) EROARE("Aflare legatura urmatoare"); if (!Introduce. In. Stiva. I(S, w)) EROARE("Introducere in stiva"); if (Vizitate[nw]==0){ Vizitate[nw] = 1; printf("vizitat nodul %dn", nw); if (!Afla. Cap(nw, &Prima. Legatura)) EROARE("Aflare prima legatura"); if (!Introduce. In. Stiva. I(S, Prima. Legatura)) EROARE("Introducere in stiva"); } } 1/13/2022 44

int main (){ int start; clrscr(); Citeste. Graf(); for (start=1; start<=NNoduri; start++) Vizitate[start]=0; for (start=1; start<=NNoduri; start++) if(Vizitate[start]==0){ printf("n. Explorare din %dn", start); if (!Explorare. In. Adancime(start)) exit(EXIT_FAILURE); } printf("nsfarsit explorare"); } 1/13/2022 45