Grafuri orientate Definiie Se numete graf orientat o

Grafuri orientate

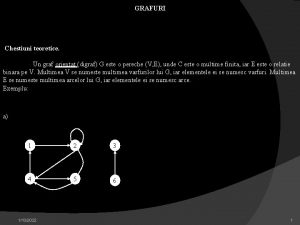
Definiţie: Se numeşte graf orientat o pereche ordonată de mulţimi ( X , U ), unde : – X este o mulţime finită şi nevidă de elemente, numite noduri sau vârfuri; – U este o mulţime de perechi ordonate din X, numite arce. X se numeşte mulţimea nodurilor sau vârfurilor U se numeşte mulţimea arcelor.

Definiţie: Pentru un arc u = [ x , y ] : – x se numeşte extremitatea iniţială, iar y se numeşte extremitatea finală a arcului; – nodurile x şi y sunt adiacente; – arcul u şi nodul x sunt incidente în graf; – arcul u şi nodul y sunt incidente în graf; – nodul y se numeşte succesor al lui x; – nodul x se numeşte predecesor al lui y. Definiţie: Un arc de forma [ x , x ] se numeşte buclă. Observaţie: [ x , y ] ≠ [ y , x ] deoarece există o orientare a arcului

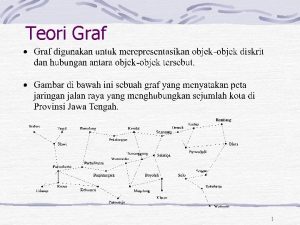
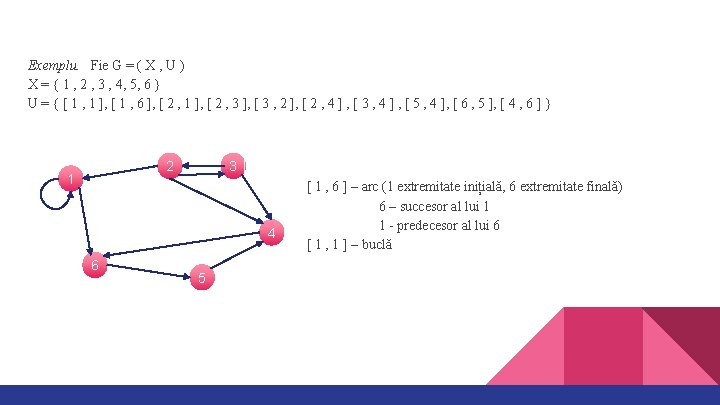
Exemplu. Fie G = ( X , U ) X = { 1 , 2 , 3 , 4, 5, 6 } U = { [ 1 , 1 ], [ 1 , 6 ], [ 2 , 1 ], [ 2 , 3 ], [ 3 , 2 ], [ 2 , 4 ] , [ 3 , 4 ] , [ 5 , 4 ], [ 6 , 5 ], [ 4 , 6 ] } 2 1 3 4 6 5 [ 1 , 6 ] – arc (1 extremitate inițială, 6 extremitate finală) 6 – succesor al lui 1 1 - predecesor al lui 6 [ 1 , 1 ] – buclă

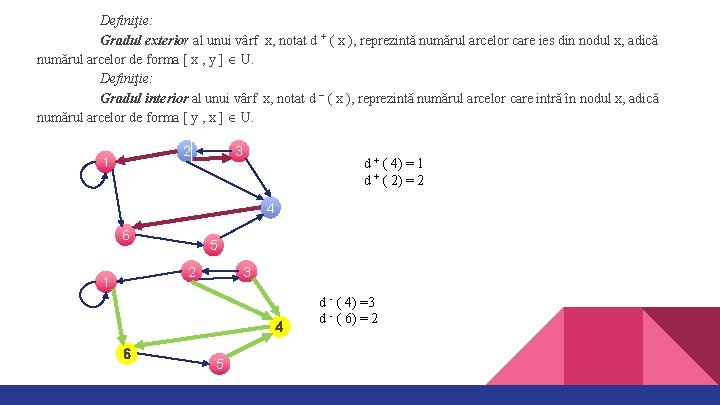
Definiţie: Gradul exterior al unui vârf x, notat d + ( x ), reprezintă numărul arcelor care ies din nodul x, adică numărul arcelor de forma [ x , y ] U. Definiţie: Gradul interior al unui vârf x, notat d – ( x ), reprezintă numărul arcelor care intră în nodul x, adică numărul arcelor de forma [ y , x ] U. 2 1 3 d + ( 4) = 1 d + ( 2) = 2 4 6 5 2 1 3 4 6 5 d - ( 4) =3 d - ( 6) = 2

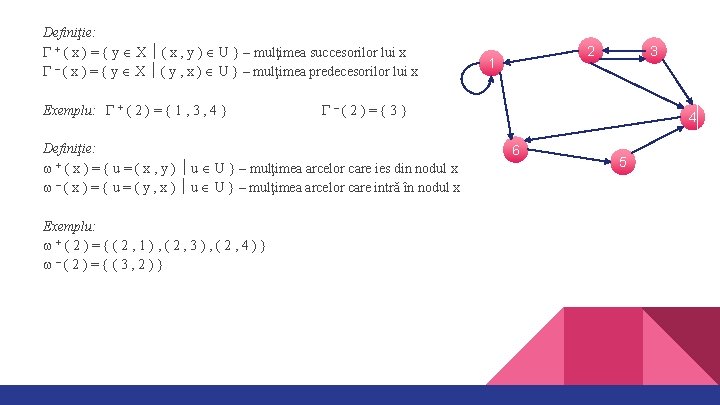
Definiţie: + ( x ) = { y X ( x , y ) U } – mulţimea succesorilor lui x – ( x ) = { y X ( y , x ) U } – mulţimea predecesorilor lui x Exemplu: + ( 2 ) = { 1 , 3 , 4 } 1 3 –(2)={3} Definiţie: + ( x ) = { u = ( x , y ) u U } – mulţimea arcelor care ies din nodul x – ( x ) = { u = ( y , x ) u U } – mulţimea arcelor care intră în nodul x Exemplu: +(2)={(2, 1), (2, 3), (2, 4)} –(2)={(3, 2)} 2 4 6 5

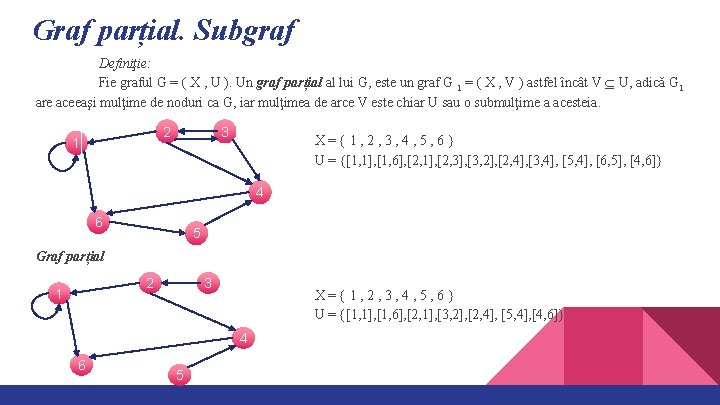
Graf parțial. Subgraf Definiţie: Fie graful G = ( X , U ). Un graf parțial al lui G, este un graf G 1 = ( X , V ) astfel încât V U, adică G 1 are aceeaşi mulţime de noduri ca G, iar mulţimea de arce V este chiar U sau o submulţime a acesteia. 2 1 3 X={1, 2, 3, 4, 5, 6} U = {[1, 1], [1, 6], [2, 1], [2, 3], [3, 2], [2, 4], [3, 4], [5, 4], [6, 5], [4, 6]} 4 6 5 Graf parțial 2 1 3 X={1, 2, 3, 4, 5, 6} U = {[1, 1], [1, 6], [2, 1], [3, 2], [2, 4], [5, 4], [4, 6]} 4 6 5

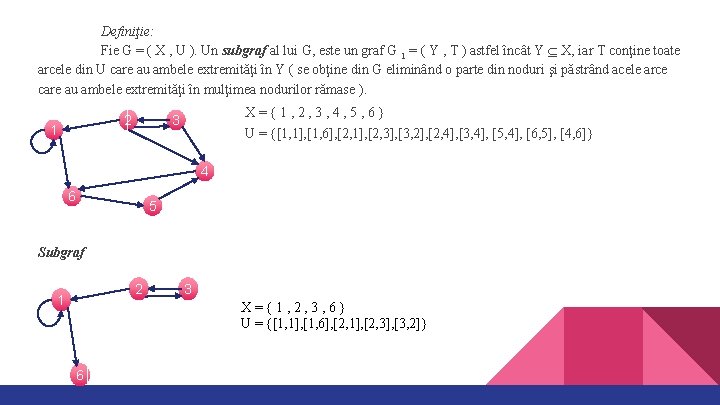
Definiţie: Fie G = ( X , U ). Un subgraf al lui G, este un graf G 1 = ( Y , T ) astfel încât Y X, iar T conţine toate arcele din U care au ambele extremităţi în Y ( se obţine din G eliminând o parte din noduri şi păstrând acele arce care au ambele extremităţi în mulţimea nodurilor rămase ). 2 1 X={1, 2, 3, 4, 5, 6} U = {[1, 1], [1, 6], [2, 1], [2, 3], [3, 2], [2, 4], [3, 4], [5, 4], [6, 5], [4, 6]} 3 4 6 5 Subgraf 2 1 3 X={1, 2, 3, 6} U = {[1, 1], [1, 6], [2, 1], [2, 3], [3, 2]} 6

Drum. Circuit Definiţie: Se numeşte drum în graful G, o succesiune de noduri D = ( z 1 , z 2 , … , zk ), unde z 1, z 2, … , zk X, astfel încât oricare două noduri consecutive sunt adiacente, adică [ z 1 , z 2 ] , [ z 2 , z 3 ] , … , [ zk– 1 , zk ] U. Nodurile z 1 şi z k se numesc extremităţile drumului. Numărul de arce care intră în componenţa sa reprezintă lungimea drumului. Dacă nodurile z 1 , z 2 , … , zk sunt distincte două câte două, drumul se numeşte elementar. În caz contrar, drumul se numeşte neelementar. Exemplu. Fie G = ( X , U ) X = { 1 , 2 , 3 , 4, 5, 6 } U = { [ 1 , 1 ], [ 1 , 6 ], [ 2 , 1 ], [ 2 , 3 ], [ 3 , 2 ], [ 2 , 4 ] , [ 3 , 4 ] , [ 5 , 4 ], [ 6 , 5 ], [ 4 , 6 ] } 2 1 3 D 1= (1, 6, 5, 4) – drum elementar de lungime 3 D 2= (2, 3, 4, 6, 5, 4) – drum neelementar de lungime 5 4 6 5

Definiţie: Se numeşte circuit într–un graf, un drum D = ( z 1 , z 2 , … , zk ) cu proprietatea că z 1 = zk şi arcele [ z 1 , z 2 ] , [ z 2 , z 3 ] , … , [ zk– 1 , zk ] sunt distincte două câte două. Dacă într–un circuit, toate nodurile cu excepţia primului şi a ultimului sunt distincte două câte două, atunci circuitul se numeşte elementar. În caz contrar, circuitul se numeşte neelementar. Exemplu. Fie G = ( X , U ) X = { 1 , 2 , 3 , 4, 5, 6 } U = { [ 1 , 1], [ 1 , 6], [ 2 , 1], [ 2 , 3], [2 , 5], [3 , 2], [2 , 4] , [3 , 4] , [5 , 4], [6 , 2], [6 , 5], [4 , 6] } 2 1 3 4 6 5 C 1= (4, 6, 5, 4) – circuit elementar de lungime 3 C 2= (2, 3, 4, 6, 2) – circuit elementar de lungime 4 C 3= (2, 3, 2, 4, 6, 2) – circuit neelementar de lungime 5

Reprezentarea grafurilor orientate ● 2 1 3 4 6 5 1 2 3 4 5 6 1 1 0 0 1 2 1 0 1 1 1 0 3 0 1 0 0 4 0 0 0 1 5 0 0 0 1 0 0 6 0 1 0

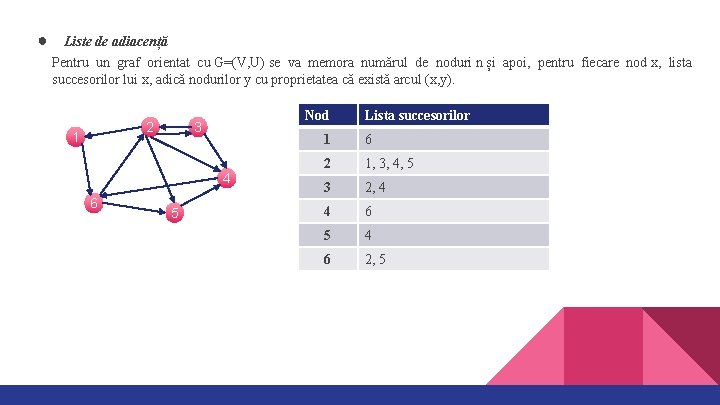
● Liste de adiacență Pentru un graf orientat cu G=(V, U) se va memora numărul de noduri n și apoi, pentru fiecare nod x, lista succesorilor lui x, adică nodurilor y cu proprietatea că există arcul (x, y). 2 1 Nod 3 4 6 5 Lista succesorilor 1 6 2 1, 3, 4, 5 3 2, 4 4 6 5 4 6 2, 5

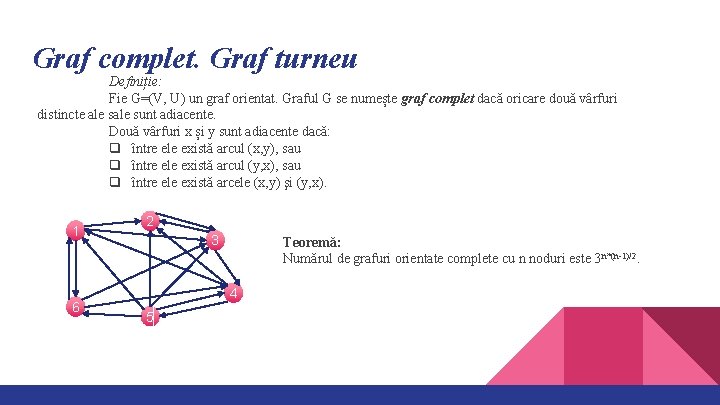
Graf complet. Graf turneu Definiție: Fie G=(V, U) un graf orientat. Graful G se numește graf complet dacă oricare două vârfuri distincte ale sunt adiacente. Două vârfuri x și y sunt adiacente dacă: q între ele există arcul (x, y), sau q între ele există arcul (y, x), sau q între ele există arcele (x, y) şi (y, x). 1 6 2 3 Teoremă: Numărul de grafuri orientate complete cu n noduri este 3 n*(n-1)/2. 4 5

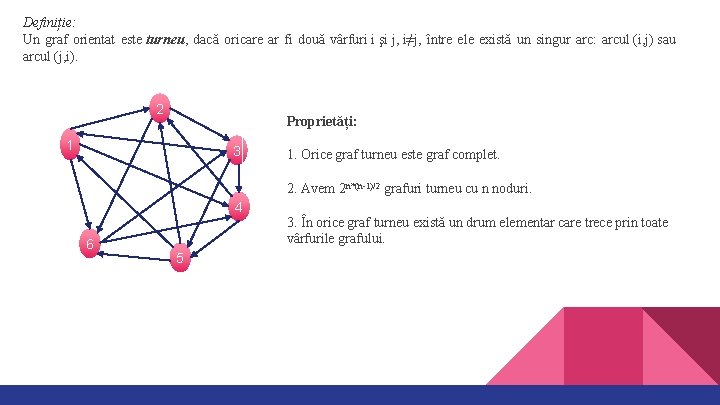
Definiție: Un graf orientat este turneu, dacă oricare ar fi două vârfuri i şi j, i≠j, între ele există un singur arc: arcul (i, j) sau arcul (j, i). 2 Proprietăți: 1 3 1. Orice graf turneu este graf complet. 2. Avem 2 n*(n-1)/2 grafuri turneu cu n noduri. 4 6 5 3. În orice graf turneu există un drum elementar care trece prin toate vârfurile grafului.

Conexitate. Tare conexitate Fie G=(V, U) un graf orientat. Graful se numește conex dacă între oricare două noduri distincte există cel puțin un lanț. Se numește componentă conexă un subgraf conex și maximal cu această calitate (adică dacă am mai adauga un nod, nar mai fi conex). Graful se numește tare conex dacă între oricare două noduri distincte există cel puțin un drum. Se numește componentă tare conexă un subgraf tare conex și maximal cu această calitate – dacă am mai adauga un nod, n-ar mai fi tare conex.

Graf hamiltonian. Graf eulerian Fie un graf orientat G=(V, U). Un drum elementar care conține toate nodurile grafului se numește drum hamiltonian. Un circuit elementar care conține toate nodurile grafului se numește circuit hamiltonian. Un graf care conține un circuit hamiltonian se numește graf hamiltonian. Un drum care conține toate arcele grafului se numește drum eulerian. Un circuit care conține toate arcele grafului se numește circuit eulerian. Un graf care conține un circuit eulerian se numește graf eulerian. Teoremă: Un graf fără noduri izolate este eulerian dacă și numai dacă este conex și pentru fiecare nod, gradul interior este egal cu cel exterior.

Aplicații Nr. crt 1. Cerința Răspuns Câte grafuri orientate, distincte, cu 4 vârfuri se pot construi? Două grafuri se consideră distincte dacă matricele lor de adiacenţă sunt diferite. a. 46 b. 26 c. 64 d. 4 (Varianta 02 – BAC 2008) 2. Se consideră un graf orientat cu 6 noduri numerotate de la 1 la 6 şi cu mulţimea arcelor formată doar din arcele: - de la fiecare nod numerotat cu un număr neprim i (i>1) la toate nodurile numerotate cu numere ce aparţin mulţimii divizorilor proprii ai lui i (divizori diferiţi de 1 şi de i) - de la nodul numerotat cu 1 la nodul numerotat cu 6 - de la fiecare nod numerotat cu un număr prim i la nodul numerotat cu i-1 Pentru graful dat, care este lungimea celui mare drum, format doar din noduri distincte? a. 6 b. 5 c. 3 d. 4 (Varianta 03 – BAC 2008) 3. Se consideră un graf orientat cu 6 noduri numerotate de la 1 la 6 şi cu mulţimea arcelor formată doar din arcele: - de la fiecare nod numerotat cu un număr neprim i (i>1) la toate nodurile numerotate cu numere ce aparţin mulţimii divizorilor proprii ai lui i (divizori diferiţi de 1 şi de i) - de la nodul numerotat cu 1 la nodul numerotat cu 6 - de la fiecare nod numerotat cu un număr prim i la nodul numerotat cu i-1 Pentru graful dat, care este lungimea celui mare drum, format doar din noduri distincte, ce uneşte nodul 6 cu nodul 1? a. 1 b. 3 c. 4 d. 6 (Varianta 04 – BAC 2008)

Nr. crt Cerința Răspuns 4. Se consideră un graf orientat cu 6 noduri care următoarele proprietăti: - suma gradelor externe ale tuturor vârfurilor grafului este egală cu 6 - sunt numai 3 vârfuri care au gradul intern egal cu 1. Care este valoarea maximă pe care o poate avea gradul extern al unui vârf din graful dat? 5. Care este numărul de grafuri orientate cu 4 vârfuri, fără circuite de lungime 1 (bucle)? a. 1048576 b. 16 c. 64 d. 4096 (Varianta 09 – BAC 2008) (Varianta 11 – BAC 2008) 6. Într-un graf orientat cu 7 noduri suma gradelor interioare ale tuturor nodurilor este egală cu 10. Care este valoarea sumei gradelor exterioare ale tuturor nodurilor? a. 5 b. 20 c. 10 d. 17 (Varianta 21 – BAC 2008) 7. 8. Care din următoarele proprietăţi este adevărată pentru un graf orientat cu n vârfuri şi n arce (n>3) care un circuit de lungime n: a. există un vârf cu gradul intern n-1 b. pentru orice vârf gradul intern şi gradul extern sunt egale c. graful nu are drumuri de lungime strict mai mare decât 2 d. gradul intern al oricărui vârf este egal cu 2 (Varianta 24 – BAC 2008) Care dintre următoarele propoziţii NU este adevărată pentru graful orientat cu 6 vârfuri, numerotate de la 1 la 6 şi ale cărui arce sunt: (2, 1), (3, 6), (4, 1), (4, 3), (4, 5), (5, 2), (6, 4)? a. vârful numerotat cu 6 aparţine unui circuit b. vârful numerotat cu 1 are gradul extern 0 c. gradul intern al vârfului numerotat cu 4 este 1 d. graful nu are circuite (Varianta 49 – BAC 2008)

Bibliografie 1. Dana Lica, Mircea Pașoi, ”Fundamentele programării – culegere de probleme pentru clasa a XI-a”, Editura L&S Soft, București, 2006 2. Emanuela Cerchez, Marinel Șerban, ”Programarea în limbajul C/C++ pentru liceu”, Editura Polirom, București, 2006 3. http: //bacinfo. cnlr. ro/ - Subiecte bacalaureat informatică