Kap 10 Graf Definisjon av graf En graf

Kap 10 Graf

Definisjon av graf En graf G er en ordnet mengde G = (V, E) hvor - V er en mengde bestående av elementer kalt punkter / noder (vertics) - E er en mengde bestående av elementer kalt kanter (edges). Hvert element e i E er gitt ved et entydig uordnet par av punkter / noder e = [u, v]

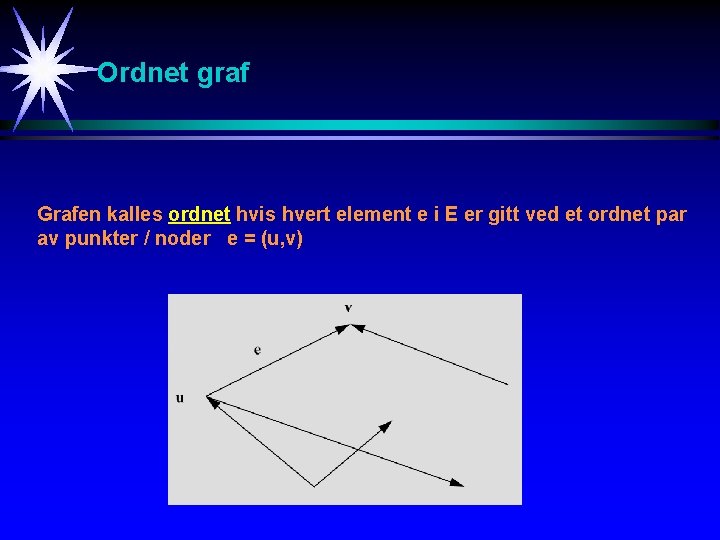
Ordnet graf Grafen kalles ordnet hvis hvert element e i E er gitt ved et ordnet par av punkter / noder e = (u, v)

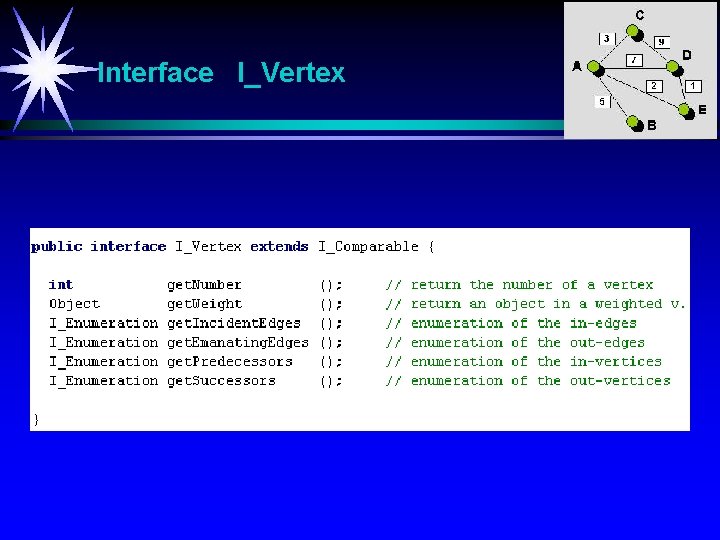
Endepunkter / Naboer Anta at e = [u, v]. u og v kalles da endepunkter til e. u og v sies også å være naboer (adjacent nodes).

Grad Med graden til u deg(u) mener vi antall elementer e i E som inneholder u.

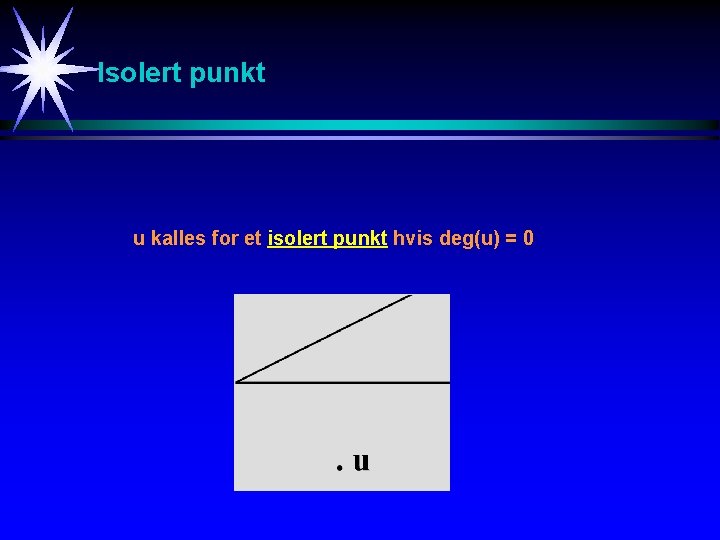
Isolert punkt u kalles for et isolert punkt hvis deg(u) = 0

Utgrad / Inngrad La G = (V, E) være en ordnet graf og la u være et element (punkt) i V. Med utgraden til u outdeg(u) mener vi antall kanter som går ut fra u. Med inngraden til u indeg(u) mener vi antall kanter som går inn til u.

Vei P av lengde n Med en vei (path) P av lengde n, Len(P) = n, mellom to punkter u og v mener vi en sekvens av n+1 punkter P = (v 0 , v 1 , v 2 , . . . . , vn) slik at u = v 0 v = vn vi-1 og vi er naboer for i = 1, 2, . . , n

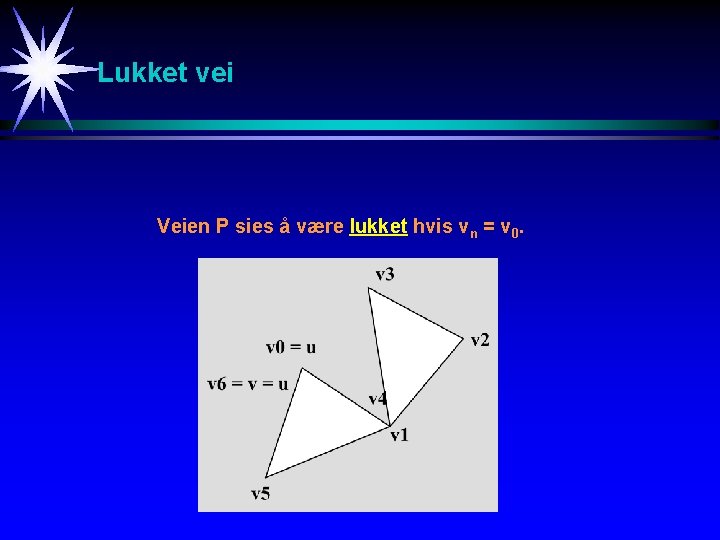
Lukket vei Veien P sies å være lukket hvis vn = v 0.

Enkel vei Veien P sies å være enkel hvis alle vi er ulike med unntak av vn som kan være lik v 0.

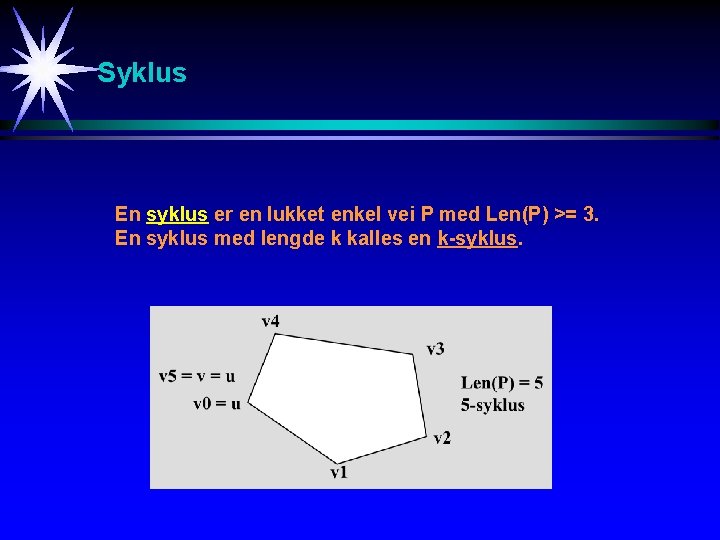
Syklus En syklus er en lukket enkel vei P med Len(P) >= 3. En syklus med lengde k kalles en k-syklus.

Sammenhengende graf En graf G = (V, E) kalles sammenhengende (connected) hvis det for hvert par av punkter u og v i V finnes en vei P mellom dem.

Komplett graf En graf G = (V, E) kalles komplett hvis hvert punkt u i V er nabo til et vilkårlig annet punkt v i V.

Tre En sammenhengende graf G uten sykluser kalles et tre.

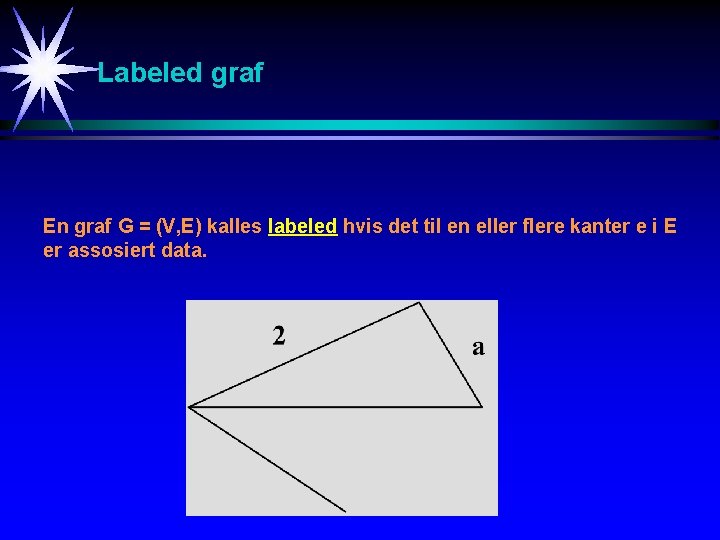
Labeled graf En graf G = (V, E) kalles labeled hvis det til en eller flere kanter e i E er assosiert data.

Vektgraf En graf G = (V, E) en vektgraf hvis det til hver kant e i E er assosiert et ikke-negativt tall w(e) kalt lengden av e. I et slikt tilfelle er hver vei P i G assosiert med en vekt w(P) som er lik summen av kantlengdene langs veien i P. 1 2 7 0

Multiple kanter Ulike kanter e 1 og e 2 kalles multiple kanter hvis de forbinder de samme endepunktene e 1 = [u, v] og e 2 = [u, v].

Loop En kant kalles en loop hvis den har identiske endepunkter e = [u, u].

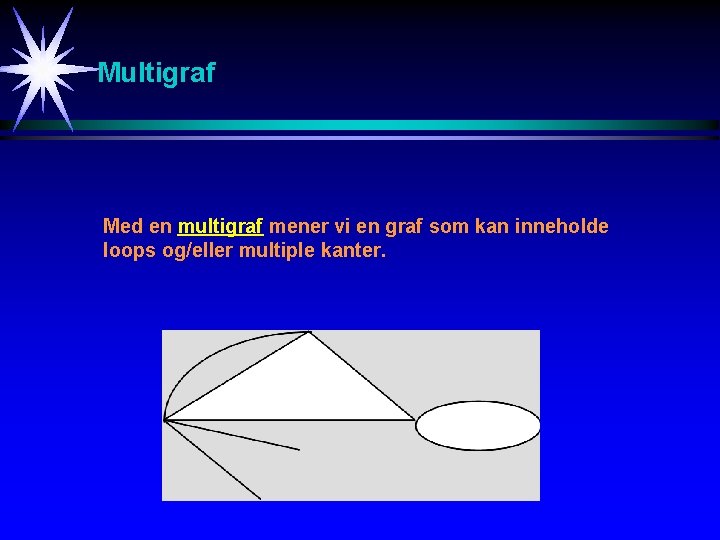
Multigraf Med en multigraf mener vi en graf som kan inneholde loops og/eller multiple kanter.

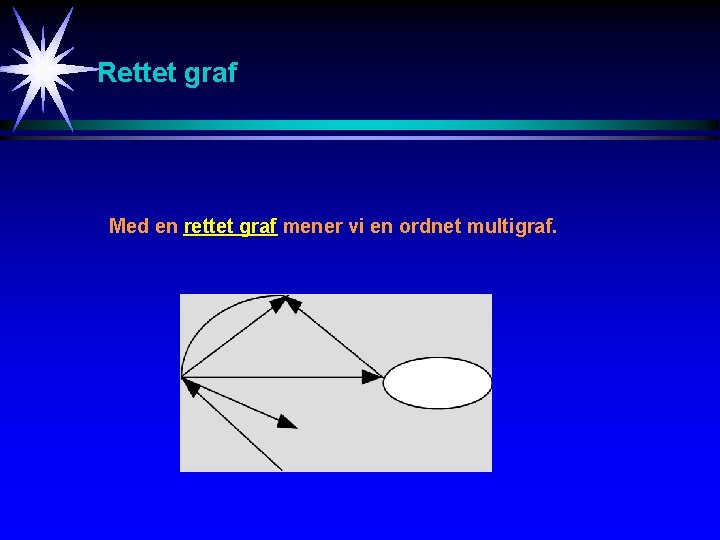
Rettet graf Med en rettet graf mener vi en ordnet multigraf.

Implementering av graf Ulike implementeringer av en graf: - Nabo-matrise - Vekt-matrise - Lenket liste

Nabo-matrise La G = (V, E) være en graf. La V inneholde n punkter v 1, v 2, v 3, …, vn. Vi definerer n x n nabo-matrisen A = (aij) ved:

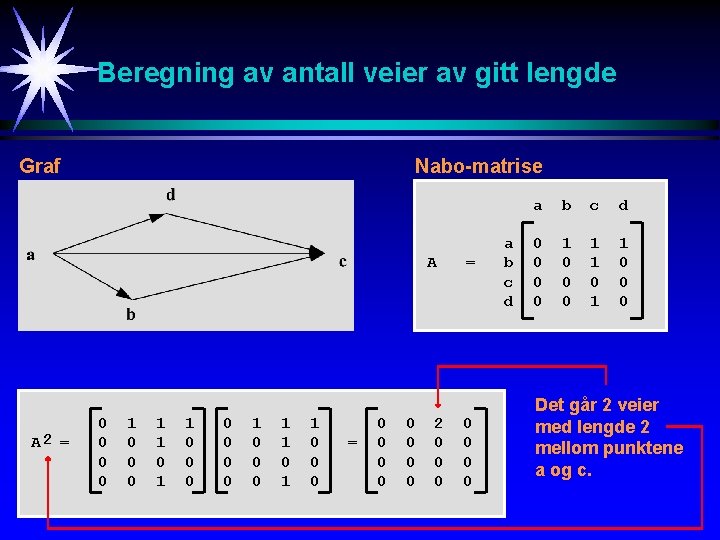
Nabo-matrise for uordnet graf Graf Nabo-matrise A = a b c d e 0 1 1 1 0 0 0 1 0 1 0 0 1 1 0 0 0 Utsagnet: Det finnes en e E slik at e = [vi, vj] er ekvivalent med utsagnet: Det finnes en e E slik at e = [vj, vi]. Herav følger at nabo-matrisen A er symmetrisk, dvs A = AT.

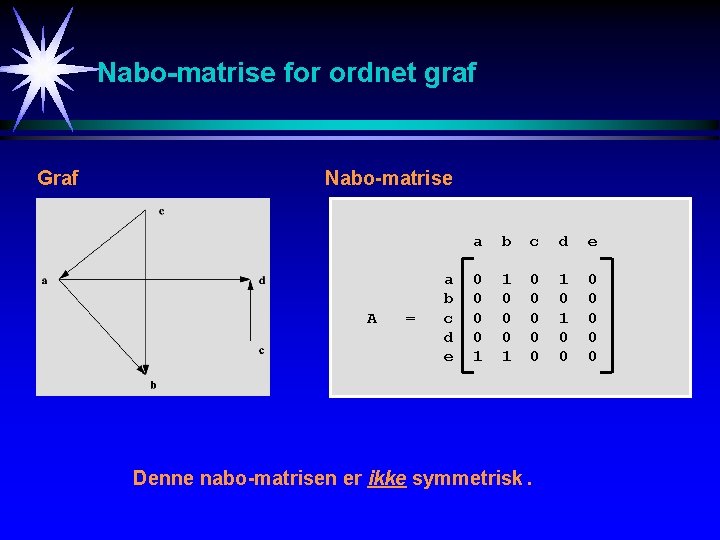
Nabo-matrise for ordnet graf Graf Nabo-matrise A = a b c d e 0 0 1 1 0 0 0 0 0 1 0 0 0 0 Denne nabo-matrisen er ikke symmetrisk.

Beregning av antall veier av gitt lengde Teorem: La A = (aij) være nabo-matrisen til grafen G. La AK = (a(K)ij) vil da angi antall veier av lengde K mellom punktene i og j. Bevis: Teoremet er opplagt sant for K = 1. Anta at påstanden er sanne for K = R-1. Vi skal vise at da er påstanden sann for K = R. Vi har: Elementet a(R)ij i matrisen A fremkommer ved følgende: a(R-1)ik angir antall veier av lengde R-1 mellom i og k akj angir antall veier av lengde 1 mellom punktene k og j. Produktet vil da angi antall veier av lengde R som går fra i til j via k. Ved å summere dette produktet over alle punkter k, vil vi få totalt antall veier av lengde R mellom i og j.

Beregning av antall veier av gitt lengde Graf Nabo-matrise A A 2 = 0 0 0 0 1 1 0 1 1 0 0 0 = 0 0 0 0 2 0 0 0 = 0 0 a b c d 0 0 1 0 0 0 1 1 0 0 0 Det går 2 veier med lengde 2 mellom punktene a og c.

Beregning av antall veier mellom to punkter AK angir antall veier av lengde K mellom to punkter Br = A + A 2 + A 3 + … + A r angir antall veier av lengde r eller mindre mellom to punkter Bn angir antall veier mellom to punkter (n = antall punkter)

Vei-matrise En vei-matrise P = (pij) defineres ved følgende: Herav får vi ( Bn = (bij) ):

Antall veier av gitt lengde - Algoritme ant. Vei (A, n, p 1, p 2, lengde) /* Finner antall veier med gitt lengde mellom to punkter. /* A : Nabo-matrisen /* n : Dimensjon til nabo-matrisen /* p 1 : Punkt nr 1 /* p 2 : Punkt nr 2 /* lengde : Gitt veilengde /* ant : Returnerer med antall veier med gitt lengde /* mellom punktene p 1 og p 2 power(A, n, lengde, k. Mat) return k. Mat(p 1, p 2) // beregner AK */ */

Vei-eksistens - Algoritme 1 Vei_Eksistens (A, n, p 1, p 2, eksist) /* Finner ut hvorvidt det eksisterer en vei mellom to gitt punkter. /* A : Nabo-matrisen /* n : Dimensjon til nabo-matrisen /* p 1 : Punkt nr 1 /* p 2 : Punkt nr 2 eksist : = False IF A(p 1, p 2) != 0 THEN eksist : = True ELSE k : = 2 WHILE (k <= n) AND (NOT eksist) DO power(A, n, k, k. Mat) IF k. Mat(p 1, p 2) != 0 THEN eksist : = True ELSE k : = k + 1 ENDIF ENDWHILE ENDIF Return eksist */ */ */

Vei-eksistens - Warsalls algoritme Vi definerer en sekvens av boolske n * n matriser Pk (inneholder 0 eller 1) ved: Warsall oppdaget følgende:

Vei-eksistens - Algoritme 2 vei_Matrise_P (A, n, P) /* Bestemmelse av veimatrisen P /* A : Nabo-matrisen /* n : Dimensjon til A og P /* P : Vei-matrisen FOR i : = 1 TO n DO FOR j : = 1 TO n DO P[i, j] : = A[i, j] ENDFOR */ */ // initiering av P FOR k : = 1 TO n DO FOR i : = 1 TO n DO FOR j : = 1 TO n DO P[i, j] : = P[i, j] v (P[i, k] ^ P[k, j]) ENDFOR P=A // oppdatering av P

Gjennomløping av en graf Dybde først gjennomløp Bredde først gjennomløp Dybde først gjennomløp kan programmeres rekursivt. Der hvor rekursiv programmering ikke benyttes, gjøres bruk av følgende: - Stakk ved dybde først gjennomløp - Kø ved bredde først gjennomløp Ved slikt gjennomløp kan vi assosiere tre ulike status-tilstander til hvert punkt i grafen: - Status = 1 : Klar status. Initieringsstatus til et punkt. - Status = 2 : Vente status. Punktet befinner seg i en stakk/kø og venter på å bli prosessert. - Status = 3 : Ferdig status. Punktet er prosessert.

Dybde først gjennomløp - Velg et startpunkt A. - Besøk en nabo til A. - Besøk naboene til A osv. Dybde_Traversal Initialiser alle punktene (status = 1) Push valgt startpunkt A til stakken og sett status(A) = 2 REPEAT Pop punktet N fra stakken Prossesser N og sett status(N) = 3 Push alle naboene (som har status = 1) til N til stakken og sett status = 2 for alle disse UNTIL stakken er tom

Dybde først gjennomløp - Rekursjon dybde_Traversal (A, n, visit) sok. Fra(k) visit[k] : = True // søking med utgangspunkt i punktet k FOR j : = 1 TO n DO IF (NOT Visit[j]) AND (A[k, j] <> NULL THEN sok. Fra(j) ENDIF ENDFOR i : = 1 TO n DO // hoved-del visit[i] : = False ENDFOR i : = 1 TO n DO IF NOT visit[i] THEN sok. Fra(i) ENDIF ENDFOR

Bredde først gjennomløping - Velg et startpunkt A. - Besøk alle naboene til A osv. Bredde_Traversal Initialiser alle punktene (Status = 1) Adder valgt startpunkt A til køen og sett Status[A] = 2 REPEAT Fjern punktet N i køen. Prosesser N og sett Status[N] = 3 Adder til køen alle naboene (med Status = 1) til N og sett Status = 2 for alle disse UNTIL køen er tom

Vekt-graf Vi skal se nærmere på en vekt-graf, dvs en graf hvor hver kant er tilordnet et ikke-negativt tall. En slik graf kalles også for et nettverk.

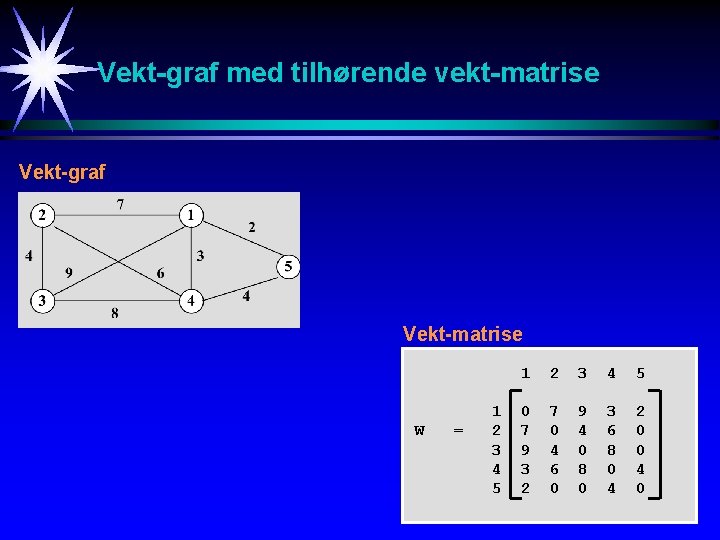
Vekt-matrise La G være en vekt-graf med n noder. La w(e) være vekten tilordnet kanten e. På samme måte som vi tidligere har laget en nabo-matrise, lager vi nå en såkalt vekt-matrise W gitt ved:

Vekt-graf med tilhørende vekt-matrise Vekt-graf Vekt-matrise W = 1 2 3 4 5 0 7 9 3 2 7 0 4 6 0 9 4 0 8 0 3 6 8 0 4 2 0 0 4 0

Minimalisering ved gjennomløping av en graf Vi skal nå forsøke å besvare følgende to spørsmål: 1. Hvordan skal vi ut fra et eksisterende nettverk hvor det finnes en vei mellom alle punktene, konstruere et nytt nettverk slik at det fremdeles finnes en vei mellom alle punktene, men nå slik at den totale summen av kantene blir mint mulig? 2. Hvordan skal vi finne den korteste veien mellom to gitte punkter?

Minimum utspent tre - Alle punktene skal være med i treet - Den totale kant-vekten er minimalisert min_Utspent_Tre Inkluder (velg) et vilkårlig punkt REPEAT FOR alle punkter NOT inkludert DO Inkluder det punktet som har en kant med minimal vekt og som samtidig er knyttet til et av punktene som allerede er inkludert Adder dette punktet og kanten til treet ENDFOR UNTIL alle punkter er inkludert

Minimum utspent tre Korteste kant fra inkludert punkt til ikke-inkludert punkt: Begynner med et vilkårlig punkt (her 1) Korteste kant fra punt 1 er kanten til punkt 5 Korteste kant er fra punkt 1 til punkt 4 Korteste kant er fra punkt 4 til punkt 2 Korteste kant er fra punkt 2 til punkt 3

Korteste vei mellom to gitte punkter Hvordan skal vi finne korteste vei mellom to gitte punkter? Vi ønsker å finne en matrise Q som er slik at qij = lengden av den korteste veien mellom vi og vj. Vi definerer en sekvens av matriser Q 0, Q 1, Q 2, …, Qn slik at: Vi sammenligner en gitt vei mellom to punkter i og j ved å sammenligne med en annen vei ved å gå innom et annet punkt k.

Korteste vei mellom to gitte punkter Vekt-graf Vekt-matrise 7 W 5 = R S T U 7 7 0 4 5 0 3 0 0 1 0 2 0 0

7 Korteste vei mellom to gitte punkter 5 7 Q 0 = 7 u 4 5 u 3 u u 1 u 2 u u RR SR UR RS TS - UT SU - 7 Q 1 = 7 u 4 5 12 3 9 u u u 1 u 2 u u RR SR UR RS SRS TS URS UT SU - 7 Q 2 = 7 10 4 5 12 3 9 u u u 1 7 2 5 11 RR SR TSR UR RS SRS TS URS UT RSU SU TSU URS 7 Q 3 = 7 10 4 5 12 3 4 u u u 1 7 2 5 6 RR SR TSR UR RS SRS TS UT RSU SU TSU UTSU 7 Q 4 = 6 9 4 5 6 3 4 8 3 6 1 7 2 5 6 RR SUR TSUR UR RS SUTS TS UTS RSUT TSUT UT RSU SU TSU UTSU 5 RSTU = 1234

Korteste vei mellom to gitte punkter 7 min_Vei (w, q, n) u : = max. Int FOR i : = 1 TO n DO FOR j : = 1 TO n DO IF w[i, j] = null THEN q[i, j] : = u ELSE q[i, j] : = w[i, j] ENDIF ENDFOR // initiering av q FOR k : = 1 TO n DO // oppdatering av q FOR i : = 1 TO n DO FOR j : = 1 TO n DO q[i, j] : = min (q[i, j], q[i, k] + q[k, j]) ENDFOR 5 5

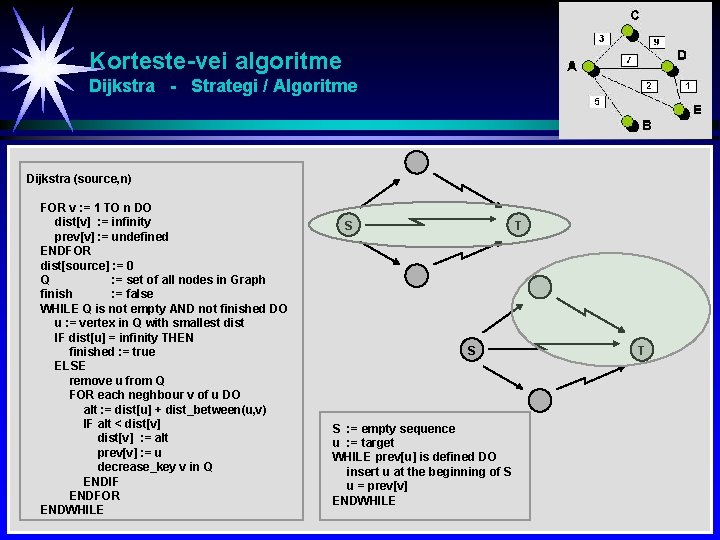
Korteste-vei algoritme Dijkstra - Strategi / Algoritme Dijkstra (source, n) FOR v : = 1 TO n DO dist[v] : = infinity prev[v] : = undefined ENDFOR dist[source] : = 0 Q : = set of all nodes in Graph finish : = false WHILE Q is not empty AND not finished DO u : = vertex in Q with smallest dist IF dist[u] = infinity THEN finished : = true ELSE remove u from Q FOR each neghbour v of u DO alt : = dist[u] + dist_between(u, v) IF alt < dist[v] : = alt prev[v] : = u decrease_key v in Q ENDIF ENDFOR ENDWHILE S T S S : = empty sequence u : = target WHILE prev[u] is defined DO insert u at the beginning of S u = prev[v] ENDWHILE T

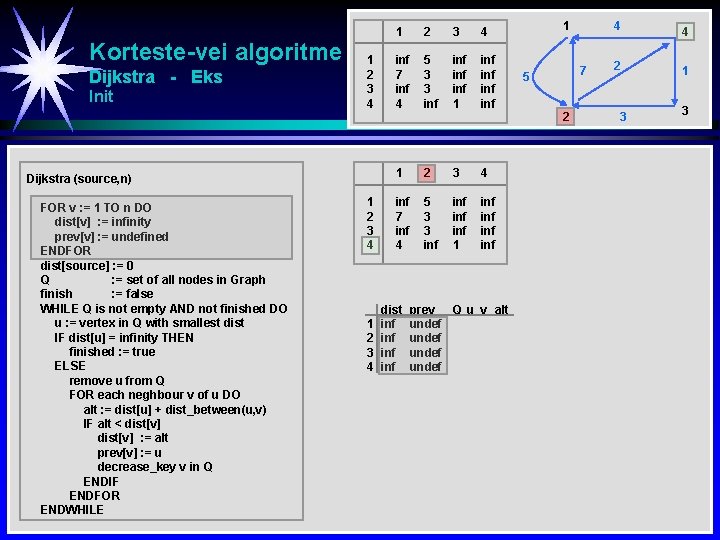
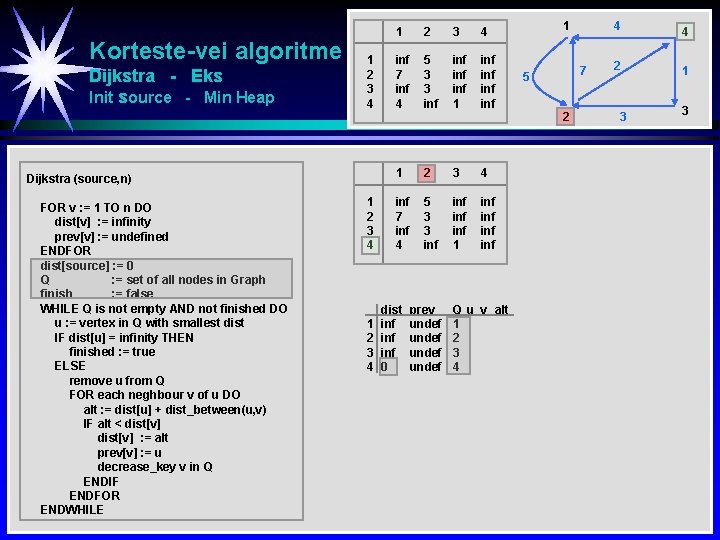
Korteste-vei algoritme Dijkstra - Eks 1 2 3 4 Dijkstra (source, n) FOR v : = 1 TO n DO dist[v] : = infinity prev[v] : = undefined ENDFOR dist[source] : = 0 Q : = set of all nodes in Graph finish : = false WHILE Q is not empty AND not finished DO u : = vertex in Q with smallest dist IF dist[u] = infinity THEN finished : = true ELSE remove u from Q FOR each neghbour v of u DO alt : = dist[u] + dist_between(u, v) IF alt < dist[v] : = alt prev[v] : = u decrease_key v in Q ENDIF ENDFOR ENDWHILE 1 2 3 4 inf 7 inf 4 5 3 3 inf inf 1 2 3 4 inf 7 inf 4 5 3 3 inf inf 1 inf inf dist prev 1 7 5 2 4 4 2 1 3 3 Q u v alt 1 2 3 4 4 S : = empty sequence u : = target WHILE prev[u] is defined DO insert u at the beginning of S u = prev[v] ENDWHILE 4 1 1 3 5 3 2

Korteste-vei algoritme Dijkstra - Eks Init 1 2 3 4 Dijkstra (source, n) FOR v : = 1 TO n DO dist[v] : = infinity prev[v] : = undefined ENDFOR dist[source] : = 0 Q : = set of all nodes in Graph finish : = false WHILE Q is not empty AND not finished DO u : = vertex in Q with smallest dist IF dist[u] = infinity THEN finished : = true ELSE remove u from Q FOR each neghbour v of u DO alt : = dist[u] + dist_between(u, v) IF alt < dist[v] : = alt prev[v] : = u decrease_key v in Q ENDIF ENDFOR ENDWHILE 1 2 3 4 inf 7 inf 4 5 3 3 inf inf 1 inf inf dist inf inf prev Q u v alt undef 1 7 5 2 4 4 2 1 3 3

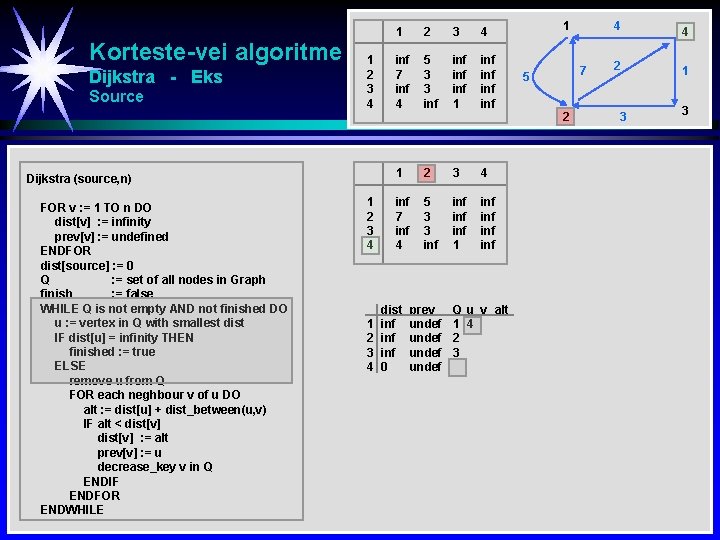
Korteste-vei algoritme Dijkstra - Eks Init source - Min Heap 1 2 3 4 Dijkstra (source, n) FOR v : = 1 TO n DO dist[v] : = infinity prev[v] : = undefined ENDFOR dist[source] : = 0 Q : = set of all nodes in Graph finish : = false WHILE Q is not empty AND not finished DO u : = vertex in Q with smallest dist IF dist[u] = infinity THEN finished : = true ELSE remove u from Q FOR each neghbour v of u DO alt : = dist[u] + dist_between(u, v) IF alt < dist[v] : = alt prev[v] : = u decrease_key v in Q ENDIF ENDFOR ENDWHILE 1 2 3 4 inf 7 inf 4 5 3 3 inf inf 1 inf inf dist inf inf 0 prev undef Q u v alt 1 2 3 4 1 7 5 2 4 4 2 1 3 3

Korteste-vei algoritme Dijkstra - Eks Source 1 2 3 4 Dijkstra (source, n) FOR v : = 1 TO n DO dist[v] : = infinity prev[v] : = undefined ENDFOR dist[source] : = 0 Q : = set of all nodes in Graph finish : = false WHILE Q is not empty AND not finished DO u : = vertex in Q with smallest dist IF dist[u] = infinity THEN finished : = true ELSE remove u from Q FOR each neghbour v of u DO alt : = dist[u] + dist_between(u, v) IF alt < dist[v] : = alt prev[v] : = u decrease_key v in Q ENDIF ENDFOR ENDWHILE 1 2 3 4 inf 7 inf 4 5 3 3 inf inf 1 inf inf dist inf inf 0 prev undef Q u v alt 1 4 2 3 1 7 5 2 4 4 2 1 3 3

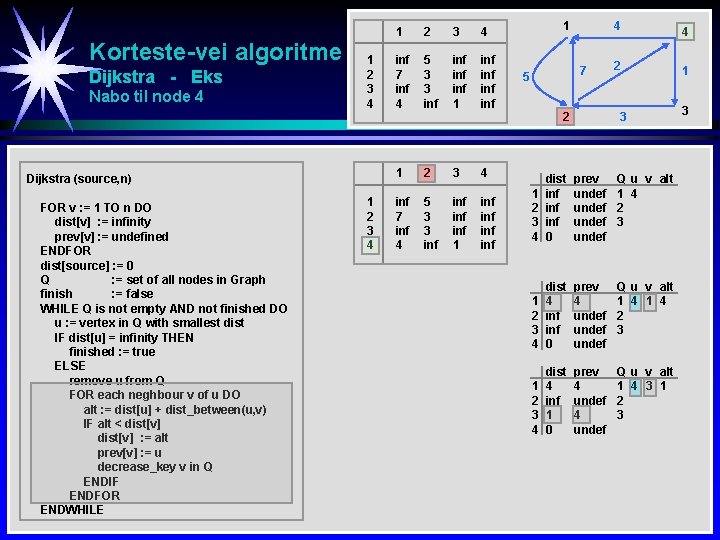
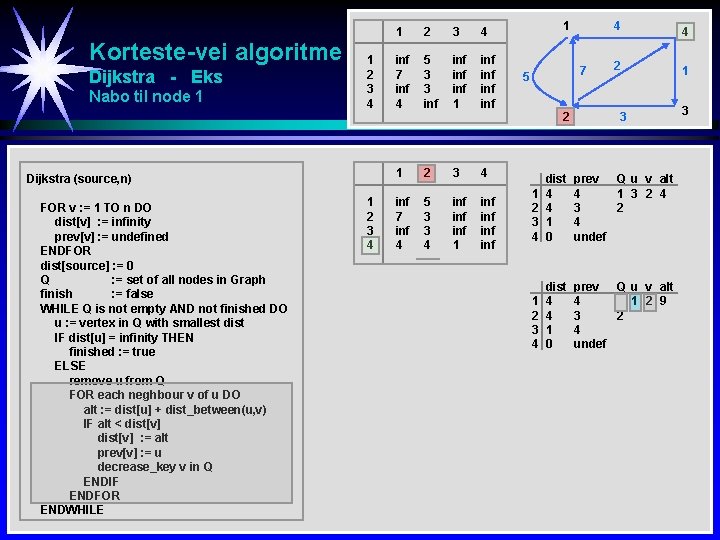
Korteste-vei algoritme Dijkstra - Eks Nabo til node 4 1 2 3 4 Dijkstra (source, n) FOR v : = 1 TO n DO dist[v] : = infinity prev[v] : = undefined ENDFOR dist[source] : = 0 Q : = set of all nodes in Graph finish : = false WHILE Q is not empty AND not finished DO u : = vertex in Q with smallest dist IF dist[u] = infinity THEN finished : = true ELSE remove u from Q FOR each neghbour v of u DO alt : = dist[u] + dist_between(u, v) IF alt < dist[v] : = alt prev[v] : = u decrease_key v in Q ENDIF ENDFOR ENDWHILE 1 2 3 4 inf 7 inf 4 5 3 3 inf inf inf inf 1 7 5 2 4 4 2 1 3 1 2 3 4 dist inf inf 0 prev undef Q u v alt 1 4 2 3 1 2 3 4 dist 4 inf 0 prev 4 undef Q u v alt 1 4 2 3 1 2 3 4 dist 4 inf 1 0 prev 4 undef Q u v alt 1 4 3 1 2 3 3

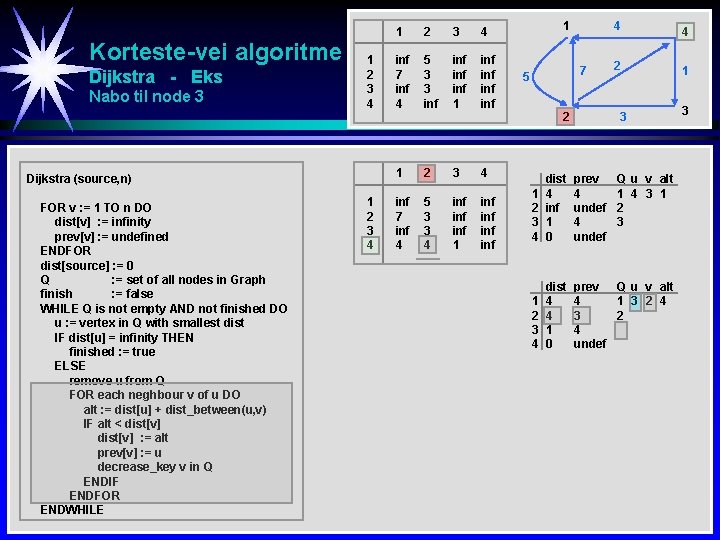
Korteste-vei algoritme Dijkstra - Eks Nabo til node 3 1 2 3 4 Dijkstra (source, n) FOR v : = 1 TO n DO dist[v] : = infinity prev[v] : = undefined ENDFOR dist[source] : = 0 Q : = set of all nodes in Graph finish : = false WHILE Q is not empty AND not finished DO u : = vertex in Q with smallest dist IF dist[u] = infinity THEN finished : = true ELSE remove u from Q FOR each neghbour v of u DO alt : = dist[u] + dist_between(u, v) IF alt < dist[v] : = alt prev[v] : = u decrease_key v in Q ENDIF ENDFOR ENDWHILE 1 2 3 4 inf 7 inf 4 5 3 3 inf inf 1 2 3 4 inf 7 inf 4 5 3 3 4 inf inf 1 7 5 2 4 4 2 1 3 1 2 3 4 dist 4 inf 1 0 prev 4 undef Q u v alt 1 4 3 1 2 3 4 dist 4 4 1 0 prev Q u v alt 4 1 3 2 4 undef 3

Korteste-vei algoritme Dijkstra - Eks Nabo til node 1 1 2 3 4 Dijkstra (source, n) FOR v : = 1 TO n DO dist[v] : = infinity prev[v] : = undefined ENDFOR dist[source] : = 0 Q : = set of all nodes in Graph finish : = false WHILE Q is not empty AND not finished DO u : = vertex in Q with smallest dist IF dist[u] = infinity THEN finished : = true ELSE remove u from Q FOR each neghbour v of u DO alt : = dist[u] + dist_between(u, v) IF alt < dist[v] : = alt prev[v] : = u decrease_key v in Q ENDIF ENDFOR ENDWHILE 1 2 3 4 inf 7 inf 4 5 3 3 inf inf 1 2 3 4 inf 7 inf 4 5 3 3 4 inf inf 1 7 5 2 4 4 2 1 3 1 2 3 4 dist 4 4 1 0 prev Q u v alt 4 1 3 2 4 undef 1 2 3 4 dist 4 4 1 0 prev Q u v alt 4 1 2 9 3 2 4 undef 3

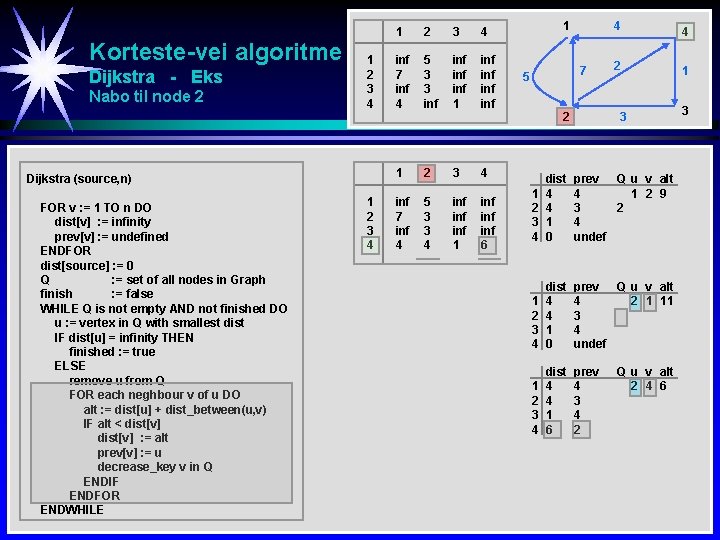
Korteste-vei algoritme Dijkstra - Eks Nabo til node 2 1 2 3 4 Dijkstra (source, n) FOR v : = 1 TO n DO dist[v] : = infinity prev[v] : = undefined ENDFOR dist[source] : = 0 Q : = set of all nodes in Graph finish : = false WHILE Q is not empty AND not finished DO u : = vertex in Q with smallest dist IF dist[u] = infinity THEN finished : = true ELSE remove u from Q FOR each neghbour v of u DO alt : = dist[u] + dist_between(u, v) IF alt < dist[v] : = alt prev[v] : = u decrease_key v in Q ENDIF ENDFOR ENDWHILE 1 2 3 4 inf 7 inf 4 5 3 3 inf inf 1 2 3 4 inf 7 inf 4 5 3 3 4 inf inf 1 inf inf 6 1 7 5 2 4 4 2 1 3 1 2 3 4 dist 4 4 1 0 prev Q u v alt 4 1 2 9 3 2 4 undef 1 2 3 4 dist 4 4 1 0 prev Q u v alt 4 2 1 11 3 4 undef 1 2 3 4 dist 4 4 1 6 prev 4 3 4 2 Q u v alt 2 4 6 3

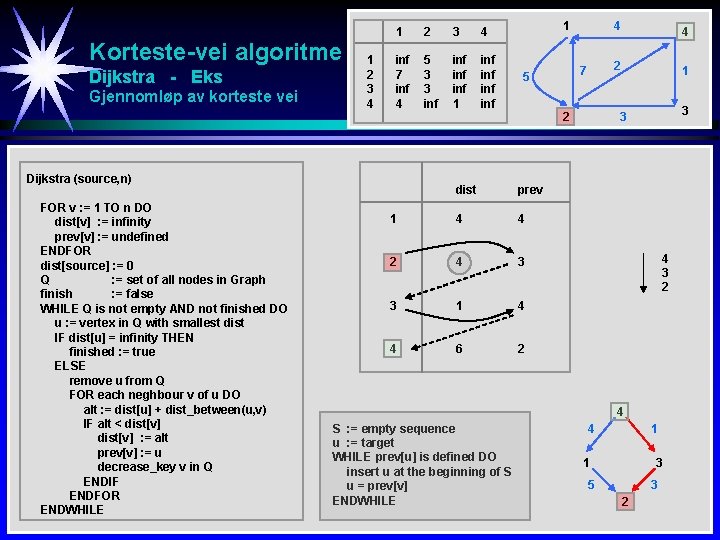
Korteste-vei algoritme Dijkstra - Eks Gjennomløp av korteste vei 1 2 3 4 inf 7 inf 4 5 3 3 inf inf 1 inf inf Dijkstra (source, n) FOR v : = 1 TO n DO dist[v] : = infinity prev[v] : = undefined ENDFOR dist[source] : = 0 Q : = set of all nodes in Graph finish : = false WHILE Q is not empty AND not finished DO u : = vertex in Q with smallest dist IF dist[u] = infinity THEN finished : = true ELSE remove u from Q FOR each neghbour v of u DO alt : = dist[u] + dist_between(u, v) IF alt < dist[v] : = alt prev[v] : = u decrease_key v in Q ENDIF ENDFOR ENDWHILE 1 7 5 2 dist prev 1 4 4 2 4 3 3 1 4 4 6 2 4 4 2 1 3 3 4 3 2 4 S : = empty sequence u : = target WHILE prev[u] is defined DO insert u at the beginning of S u = prev[v] ENDWHILE 4 1 1 3 5 3 2

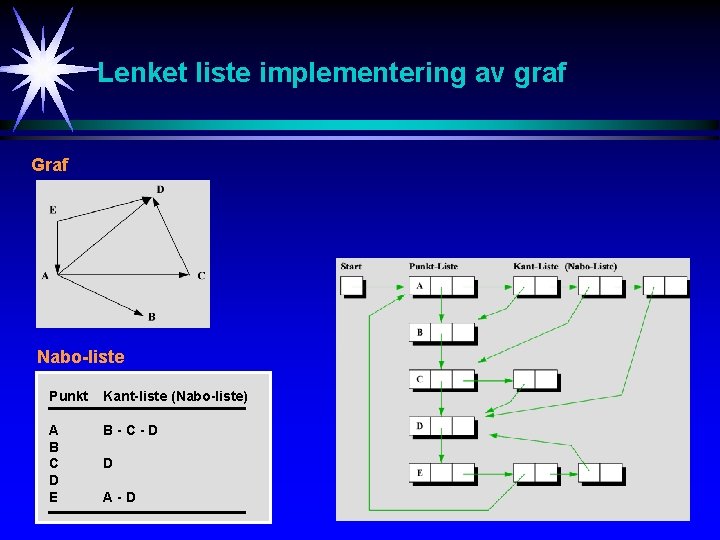
Lenket liste implementering av graf Graf Nabo-liste Punkt Kant-liste (Nabo-liste) A B C D E B-C-D D A-D

Innsetting Start : PLed : KLed : Pkt : NPkt : FKant: Pkant: NKant: Start-peker til første punkt i Punkt-listen Peker til første ledige i Kant-listen Info-felt i Punkt-listen Peker til neste punkt i Punkt-listen Peker til første kant Peker som viser hvilket punkt som svarer til denne kanten Peker til neste kant

finn. Element (pkt, n. Pkt, start, post, lok) /* Søker etter posten med innhold post i tabellen pkt /* og returnerer med lokasjonen til denne posten. /* post : Innhold i søkt Post /* lok : Returnerer med lokasjonen (posisjonen) /* til søkt Post (returnerer med verdien NULL /* hvis posten ikke finnes) null : = 0 lok : = null peker : = start WHILE (peker != null) AND (lok = null) DO IF post = pkt[peker] THEN lok : = peker ELSE peker : = n. Pkt[peker] ENDIF ENDWHILE */ */ */

finn. Kant(pkt, n. Pkt, f. Kant, p. Kant, n. Kant, start, post 1, post 2, lok 1, lok 2, flag) /* Søker etter en gitt kant i kant-tabellen og returnerer med lokasjonen til denne kanten. /* post 1 : Første punkt i søkt kant /* post 2 : Andre punkt i søkt kant /* lok 1 : Returnerer med lokasjonen (posisjonen) til første punkt i søkt kant /* (returnerer med verdien null hvis posten ikke finnes /* lok 2 : Returnerer med lokasjonen (posisjonen) til andre punkt i søkt kant */ /* (returnerer med verdien null hvis posten ikke finnes) /* flag : Returnerer med verdien true hvis det finnes en kant mellom post 1 og post 2 null : = 0 flag : = false finn. Element (pkt, n. Pkt, start, post 1, lok 1) finn. Element (pkt, n. Pkt, start, post 2, lok 2) IF (lok 1 != null) AND (lok 2 != null) THEN finn. Element(p. Kant, n. Kant, f. Kant[lok 1], lok 2, lok) IF lok != null THEN flag : = true ENDIF */ */

innsett. Punkt (pkt, n. Pkt, f. Kant, start, pled, post, full) /* Setter inn nytt punkt først i punkt-listen */ /* post : Nytt punkt som skal innsettes */ null: = 0 IF pled = null THEN full : = true ELSE full : = false ny : = pled : = n. Pkt[ny] pkt[ny] : = post f. Kant[ny] : = null n. Pkt[ny] : = start : = ny ENDIF // Pkt-listen er full // Ledig plass i Pkt-listen

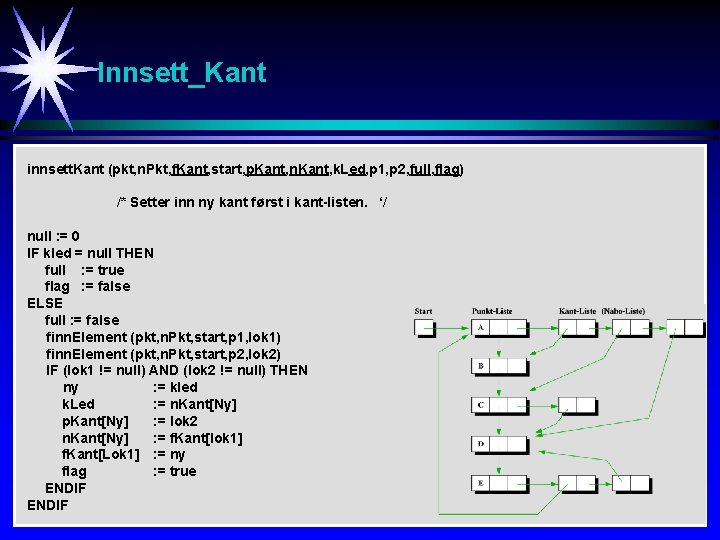
Innsett_Kant innsett. Kant (pkt, n. Pkt, f. Kant, start, p. Kant, n. Kant, k. Led, p 1, p 2, full, flag) /* Setter inn ny kant først i kant-listen. ‘/ null : = 0 IF kled = null THEN full : = true flag : = false ELSE full : = false finn. Element (pkt, n. Pkt, start, p 1, lok 1) finn. Element (pkt, n. Pkt, start, p 2, lok 2) IF (lok 1 != null) AND (lok 2 != null) THEN ny : = kled k. Led : = n. Kant[Ny] p. Kant[Ny] : = lok 2 n. Kant[Ny] : = f. Kant[lok 1] f. Kant[Lok 1] : = ny flag : = true ENDIF

fjern. Element (info, neste, start, led, post, flag) null : = 0 flag : = false IF start != null THEN IF post = info[head] THEN peker : = start : = neste[peker] : = led : = peker flag : = true ELSE forrige : = start peker : = neste[start] WHILE (peker != n. ULL) AND (NOT flag) DO IF post = info[peker] THEN neste[forrige] : = neste[peker] : = led : = peker flag : = true ELSE forrige : = peker : = neste[peker] ENDIF ENDWHILE ENDIF // Fjerner et gitt element i en åpen forlengs liste // Slette første Post // Slette post ute i listen

fjern. Punkt (pkt, n. Pkt, f. Kant, start, p. Led, p. Kant, n. Kant, k. Led, post, flag) /* Fjerner et gitt punkt samt kanter tilhørende dette punktet */ null : = 0 finn. Element (pkt, n. Pkt, start, post, lok) // Punktet som skal fjernes IF lok = null THEN Flag : = False ELSE peker : = start WHILE peker != null DO // Fjern inngående kanter til Post fjern. Element (p. Kant, n. Kant, f. Kant[peker], k. Led, lok, flag) peker : = n. Pkt[peker] ENDWHILE IF f. Kant[Lok] != NULL THEN // Fjern utgående kanter fra Post beg : = f. Kant[lok] end : = f. Kantlok] peker : = n. Kant[end] WHILE peker != null DO end : = peker : = n. Kant[peker] ENDWHILE n. Kant[end] : = k. Led : = beg ENDIF fjern. Element (pkt, n. Pkt, start, pled, post, flag) // Fjern Post ENDIF

fjern. Kant (pkt, n. Pkt, f. Kant, start, p. Kant, n. Kant, k. Led, p 1, p 2, flag) /* Fjerner en gitt kant i kant-listen /* p 1 : Første punkt i kanten som skal slettes /* p 2 : Andre punkt i kanten som skal slettes /* flag : Returnerer med verdien True /* hvis slettingen er ok */ */ */ finn. Element (pkt, n. Pkt, start, p 1, lok 1) finn. Element (pkt, n. Pkt, start, p 2, lok 2) fjern. Element (p. Kant, n. Kant, f. Kant[lok 1], k. Led, lok 2, flag)

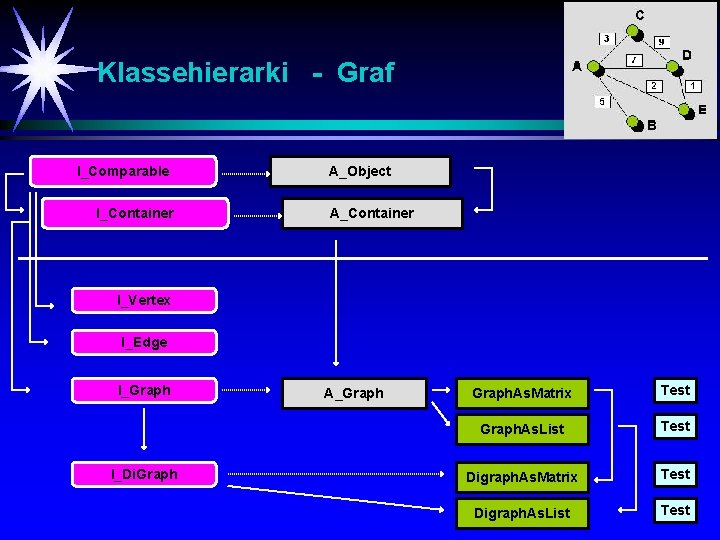
Klassehierarki - Graf I_Comparable I_Container A_Object A_Container I_Vertex I_Edge I_Graph I_Di. Graph A_Graph. As. Matrix Test Graph. As. List Test Digraph. As. Matrix Test Digraph. As. List Test

Interface I_Vertex

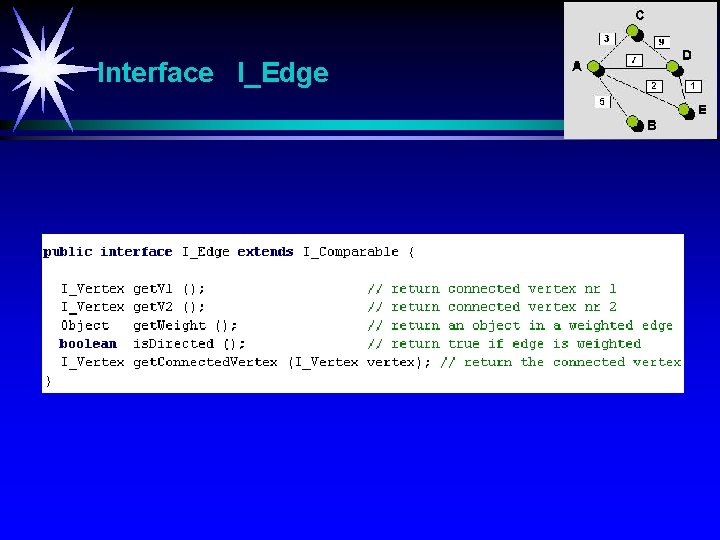
Interface I_Edge

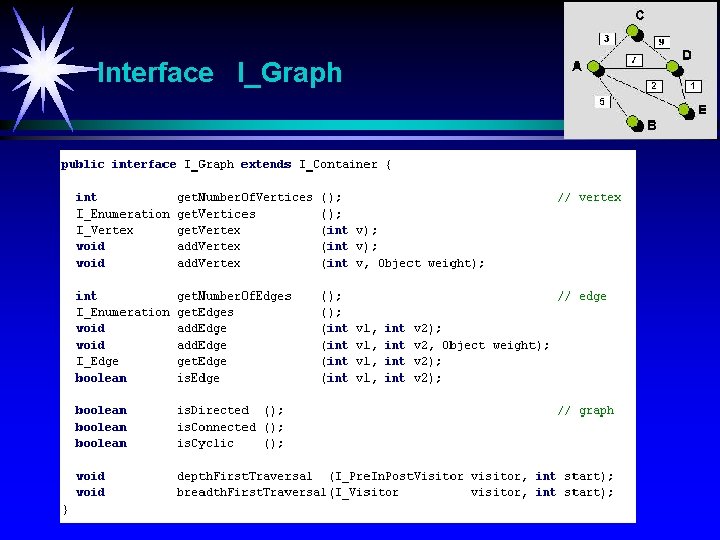
Interface I_Graph

Interface I_Graph

Abstrakt klasse A_Graph

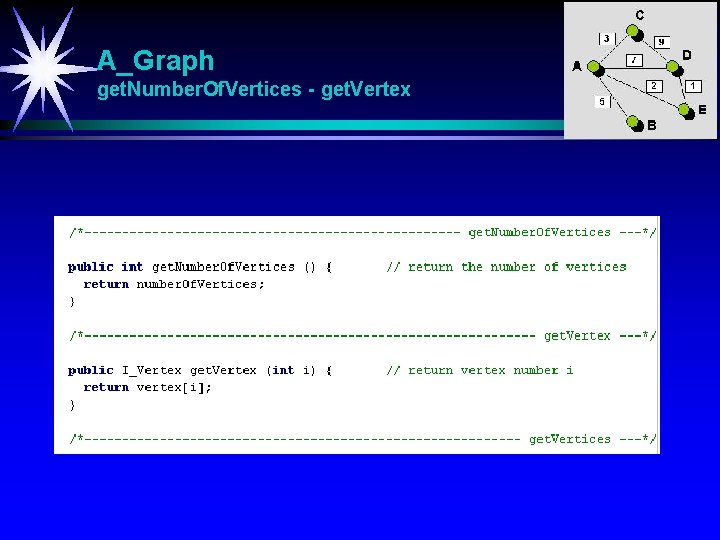
A_Graph get. Number. Of. Vertices - get. Vertex

A_Graph get. Vertices

A_Graph add. Vertex

A_Graph get. Number. Of. Edges - get. Edge – get. Edges add. Edge - is. Edge

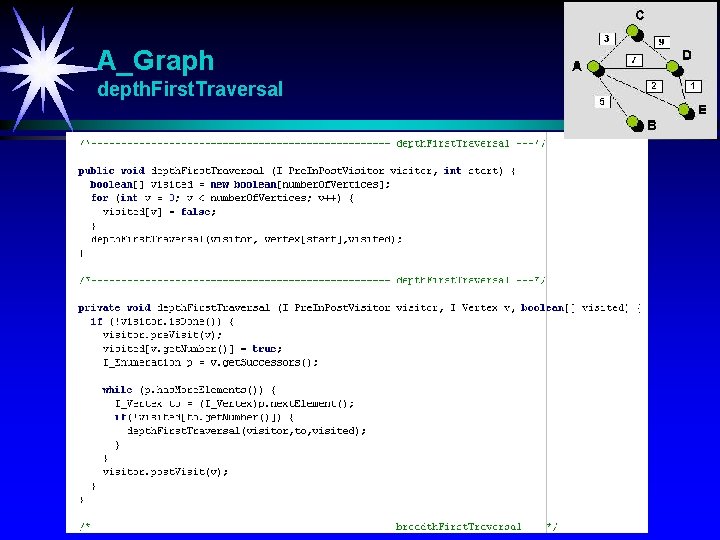
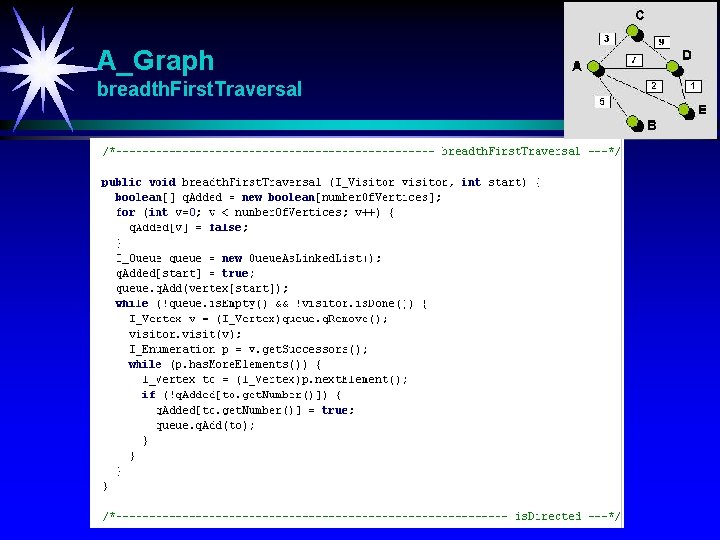
A_Graph depth. First. Traversal

A_Graph breadth. First. Traversal

A_Graph is. Directed

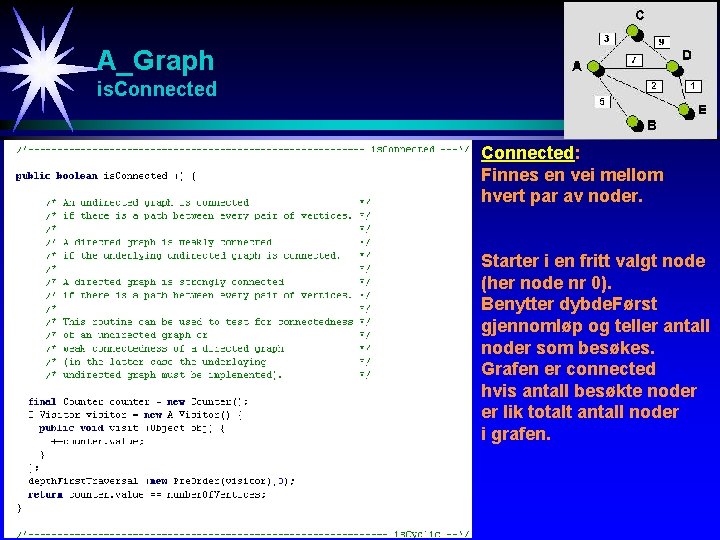
A_Graph is. Connected: Finnes en vei mellom hvert par av noder. Starter i en fritt valgt node (her node nr 0). Benytter dybde. Først gjennomløp og teller antall noder som besøkes. Grafen er connected hvis antall besøkte noder er lik totalt antall noder i grafen.

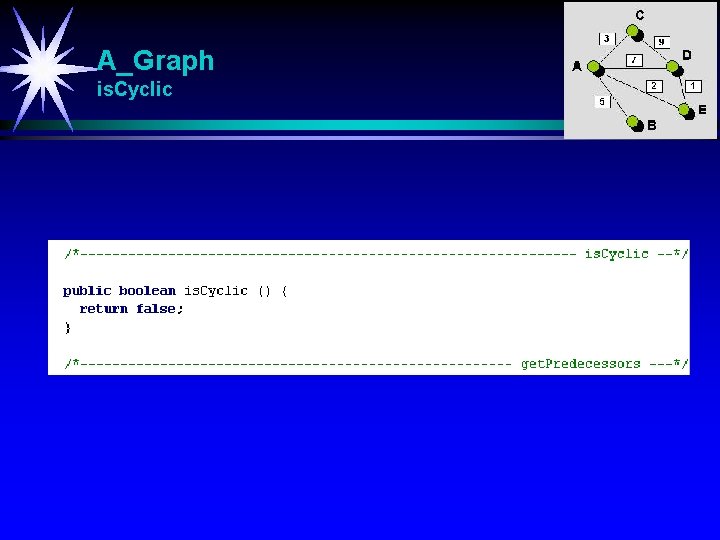
A_Graph is. Cyclic

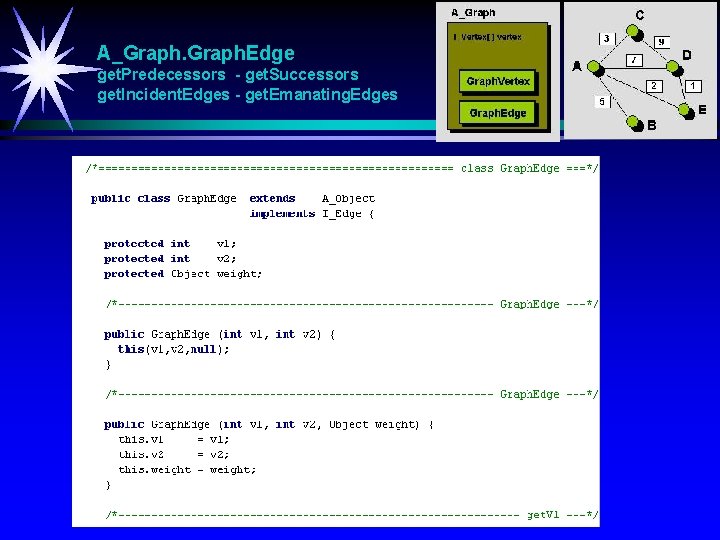
A_Graph get. Predecessors - get. Successors get. Incident. Edges - get. Emanating. Edges

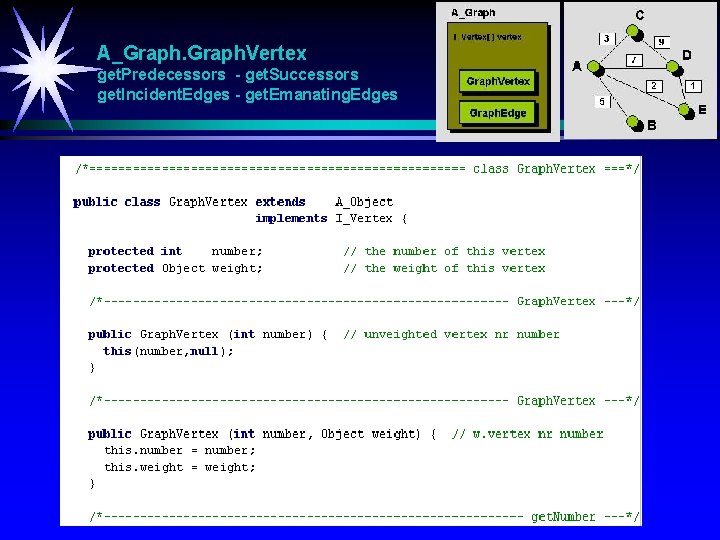
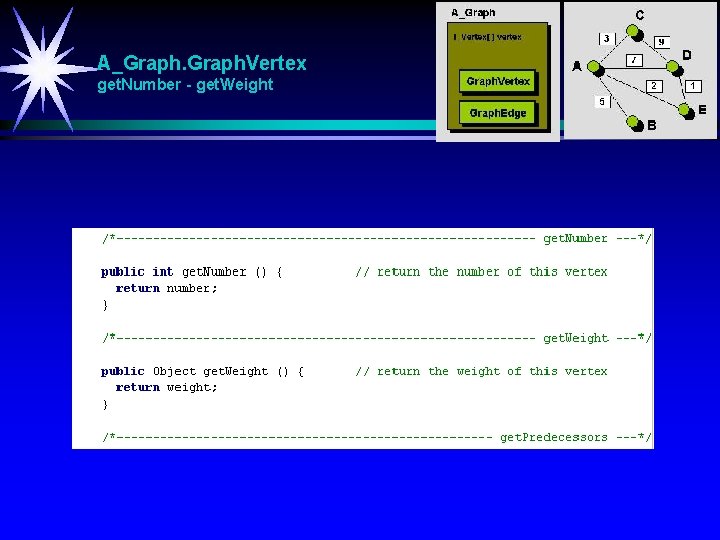
A_Graph. Vertex get. Predecessors - get. Successors get. Incident. Edges - get. Emanating. Edges

A_Graph. Vertex get. Number - get. Weight

A_Graph. Vertex get. Predecessors - get. Successors get. Incident. Edges - get. Emanating. Edges

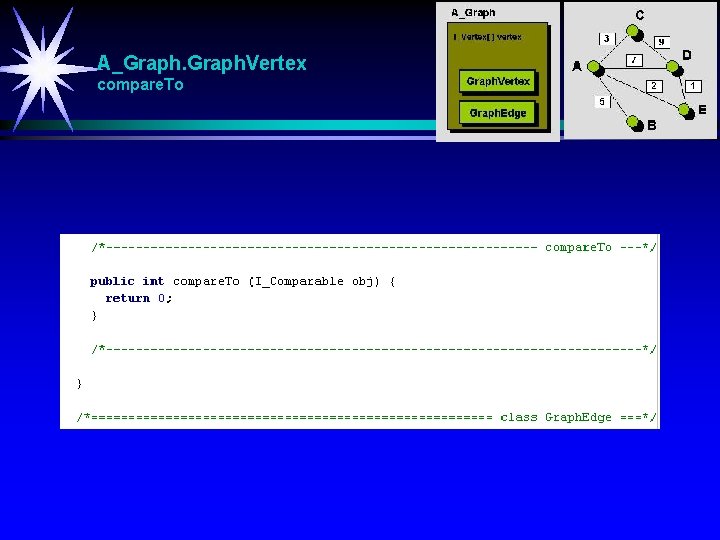
A_Graph. Vertex compare. To

A_Graph. Edge get. Predecessors - get. Successors get. Incident. Edges - get. Emanating. Edges

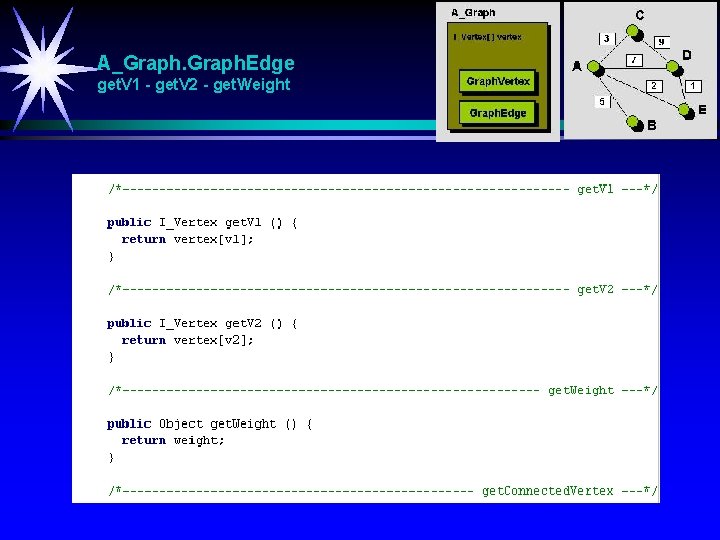
A_Graph. Edge get. V 1 - get. V 2 - get. Weight

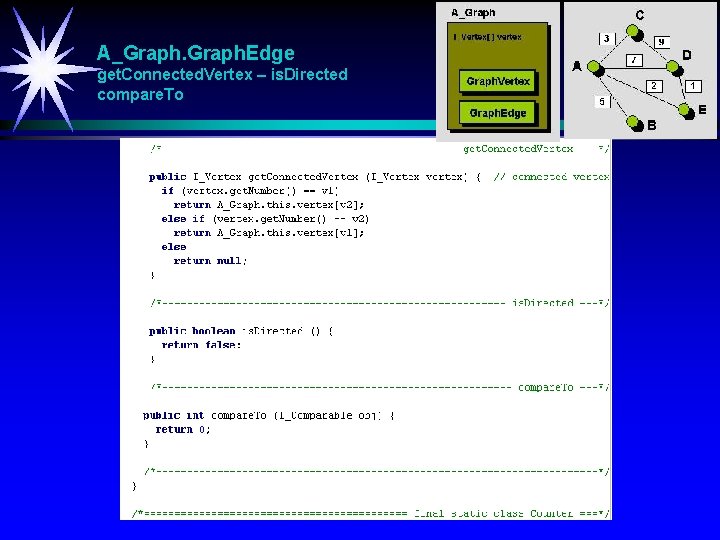
A_Graph. Edge get. Connected. Vertex – is. Directed compare. To

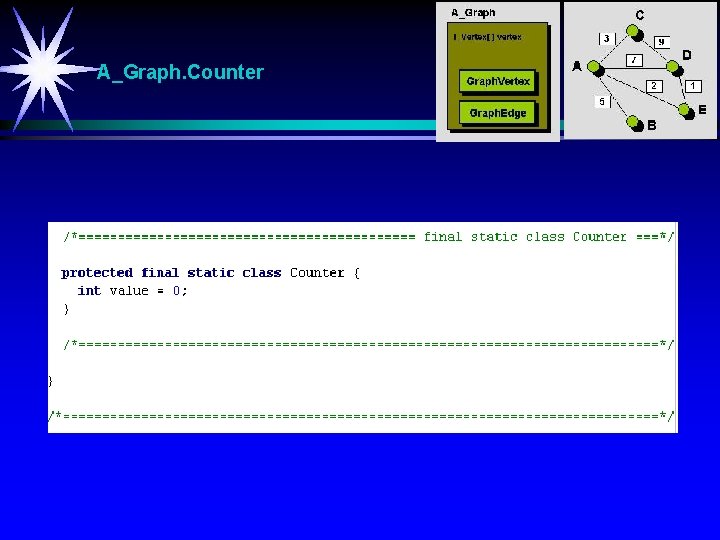
A_Graph. Counter

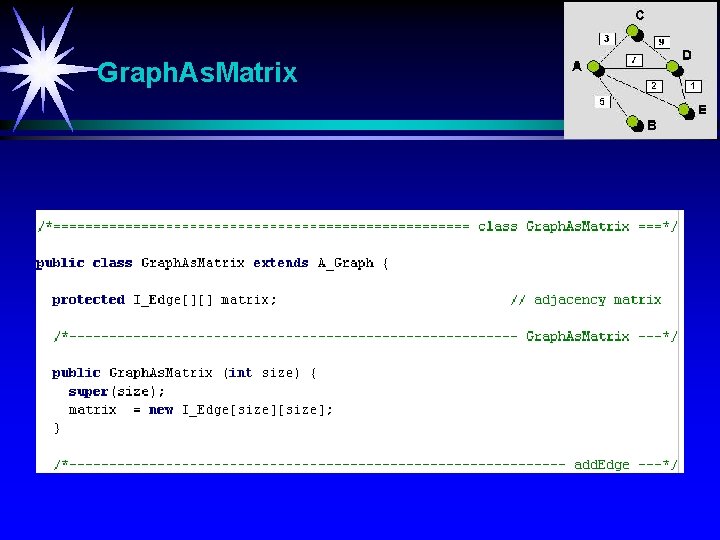
Graph. As. Matrix

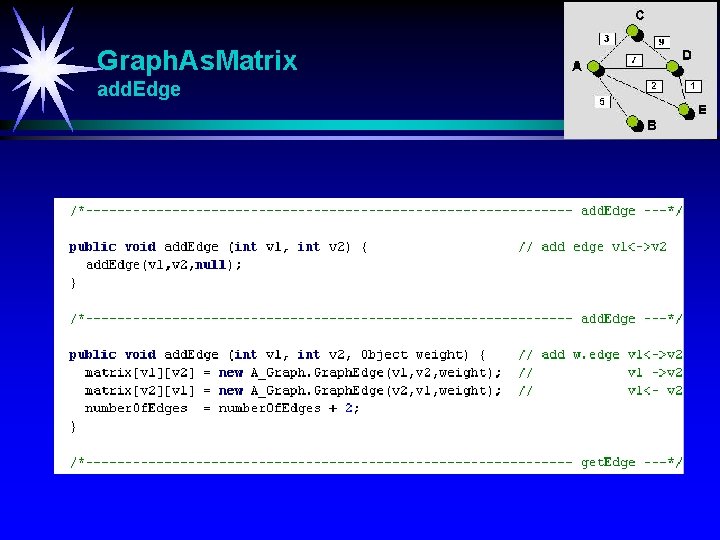
Graph. As. Matrix add. Edge

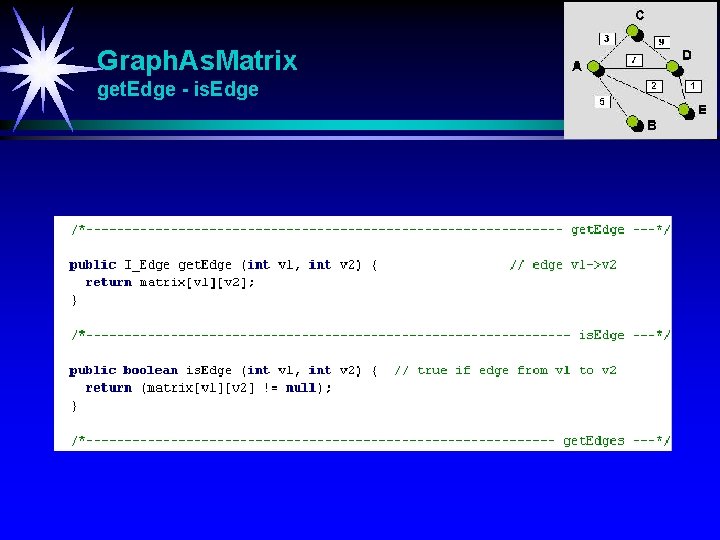
Graph. As. Matrix get. Edge - is. Edge

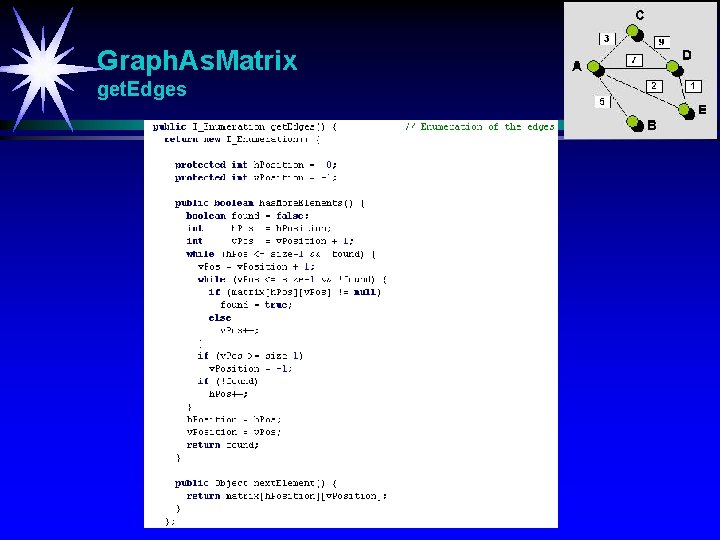
Graph. As. Matrix get. Edges

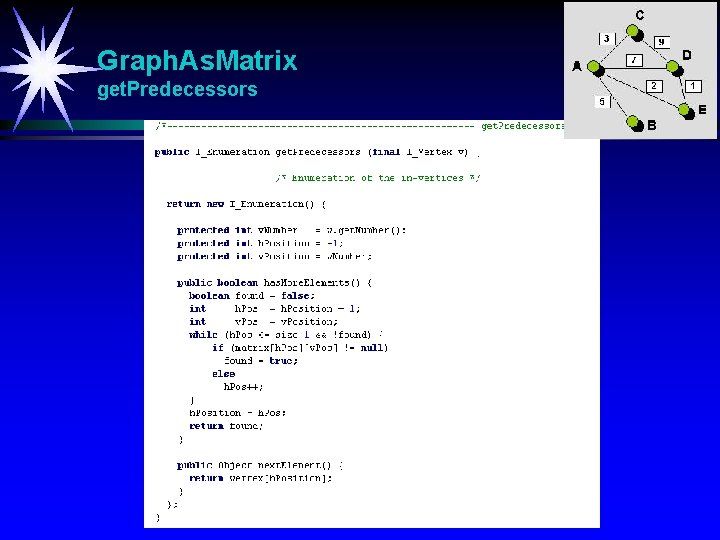
Graph. As. Matrix get. Predecessors

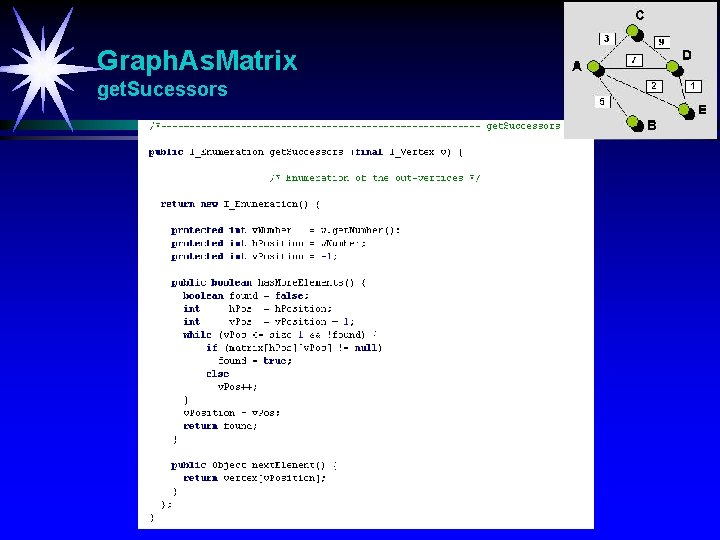
Graph. As. Matrix get. Sucessors

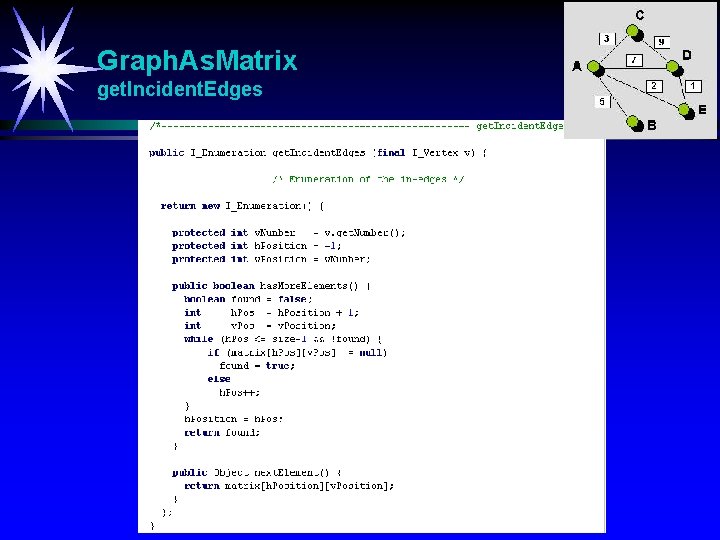
Graph. As. Matrix get. Incident. Edges

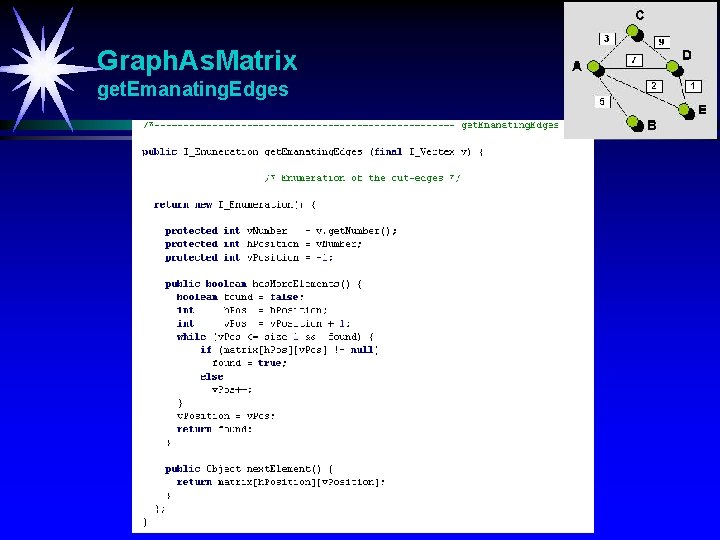
Graph. As. Matrix get. Emanating. Edges

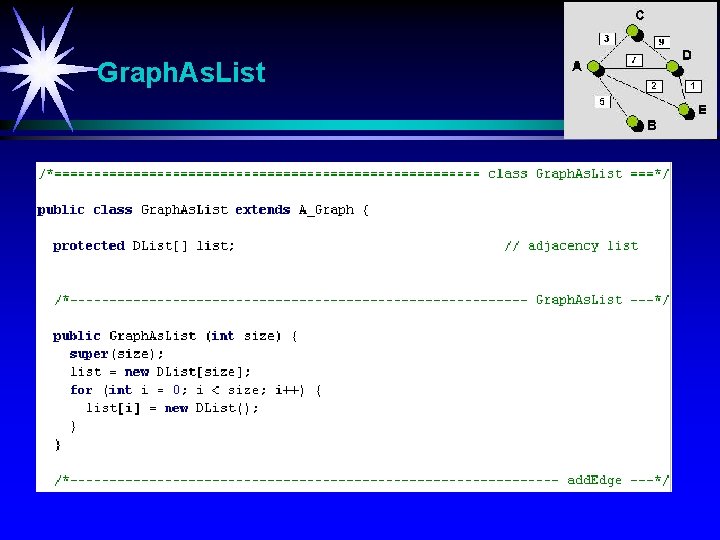
Graph. As. List

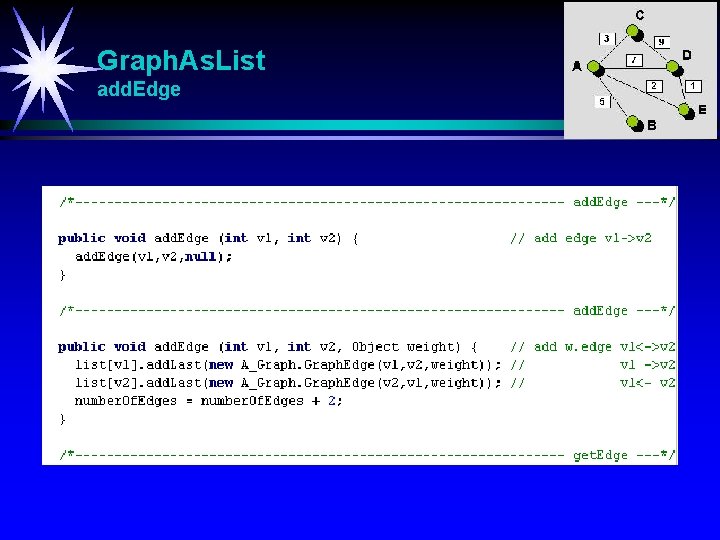
Graph. As. List add. Edge

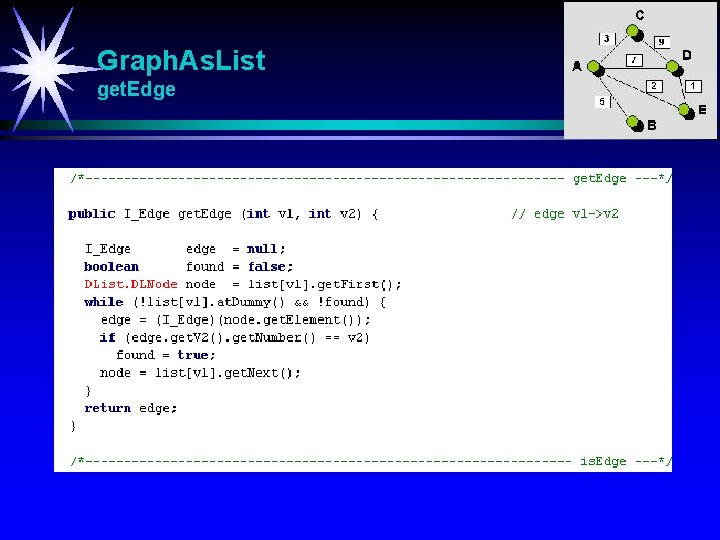
Graph. As. List get. Edge

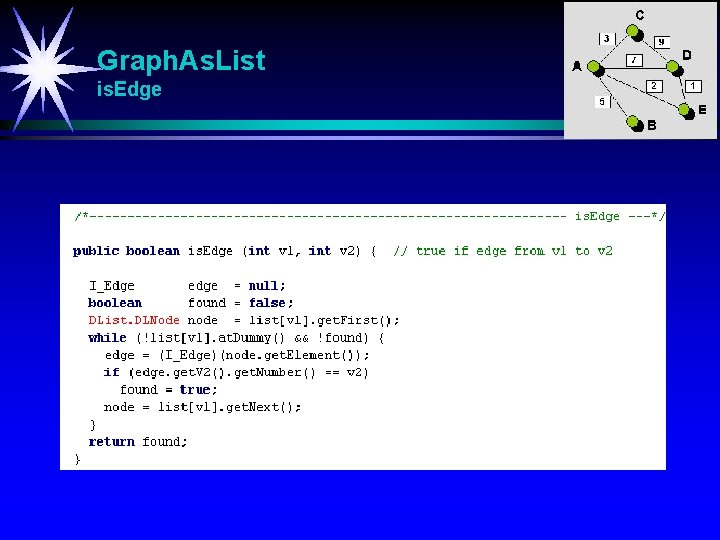
Graph. As. List is. Edge

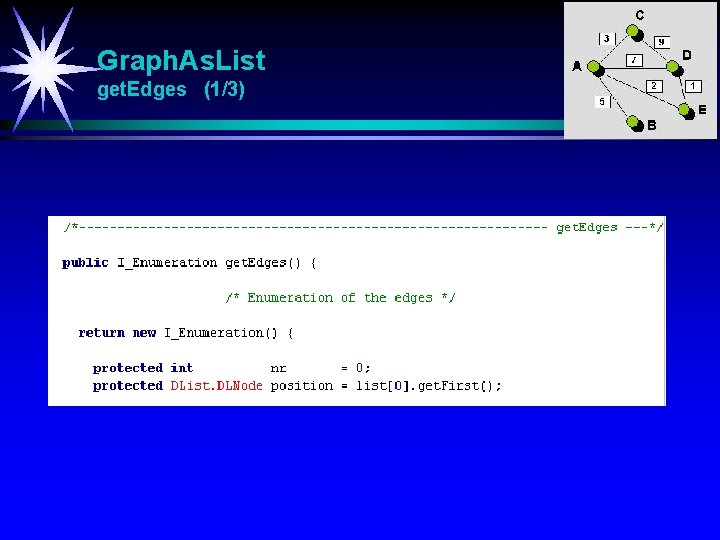
Graph. As. List get. Edges (1/3)

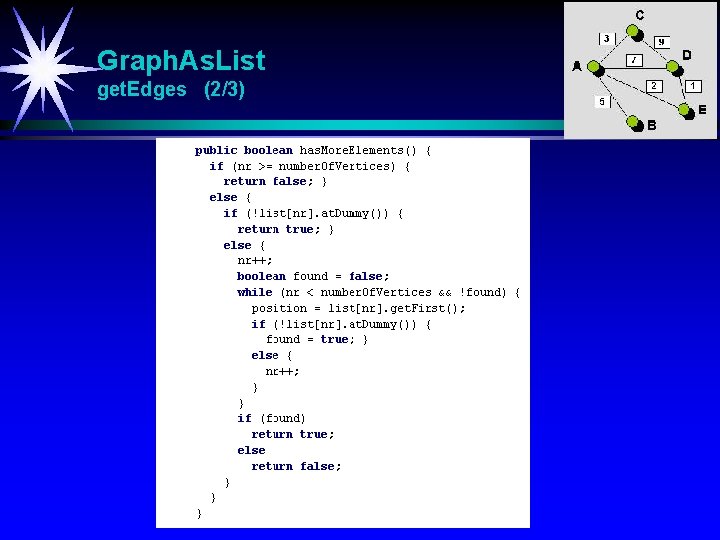
Graph. As. List get. Edges (2/3)

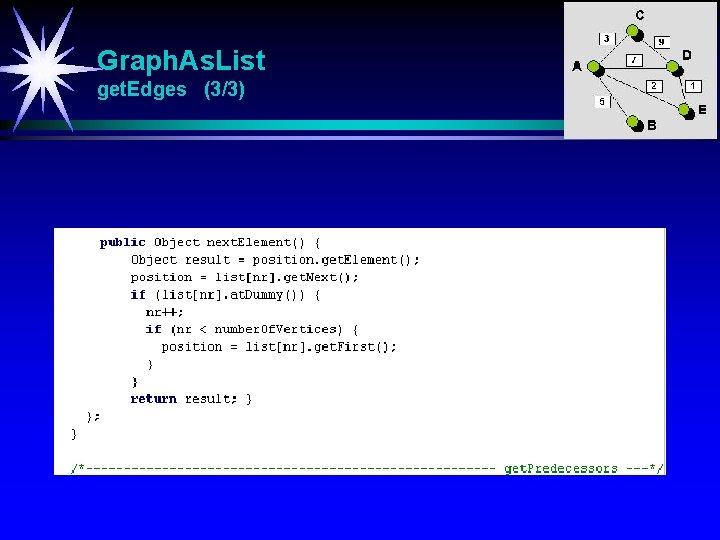
Graph. As. List get. Edges (3/3)

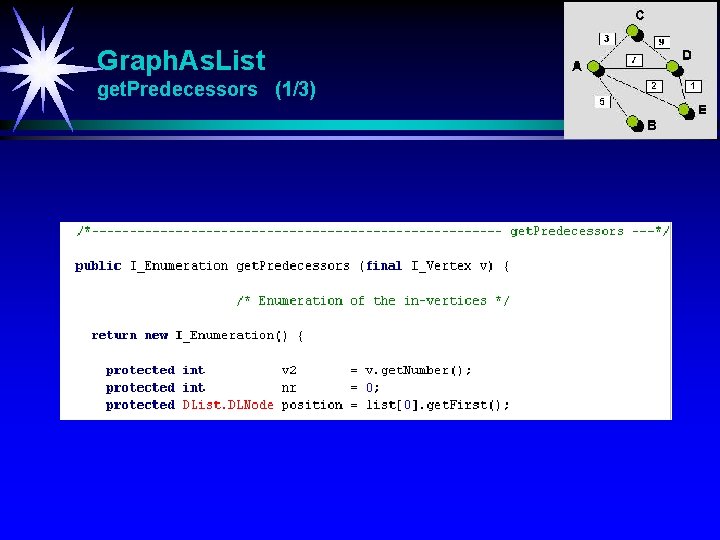
Graph. As. List get. Predecessors (1/3)

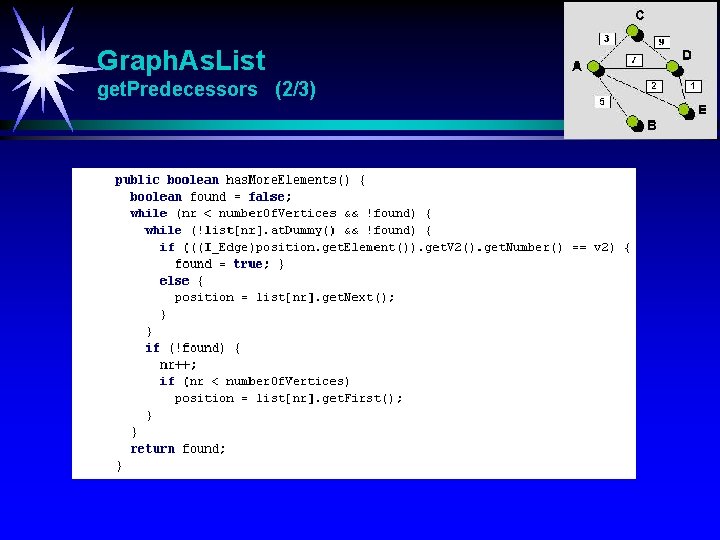
Graph. As. List get. Predecessors (2/3)

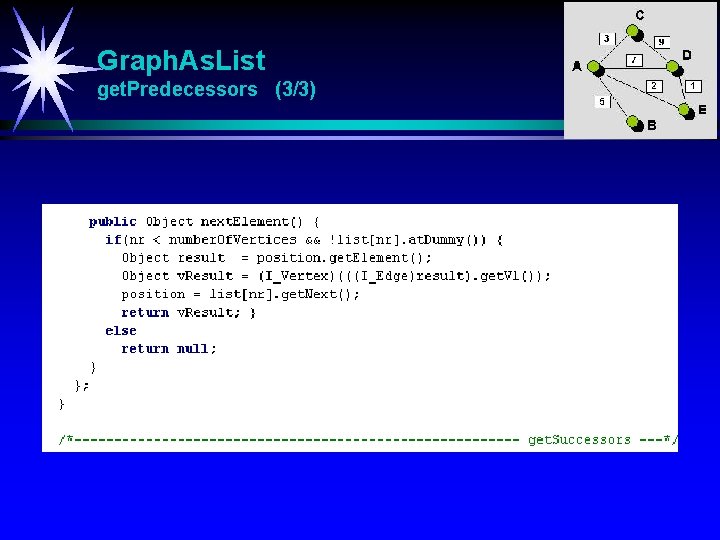
Graph. As. List get. Predecessors (3/3)

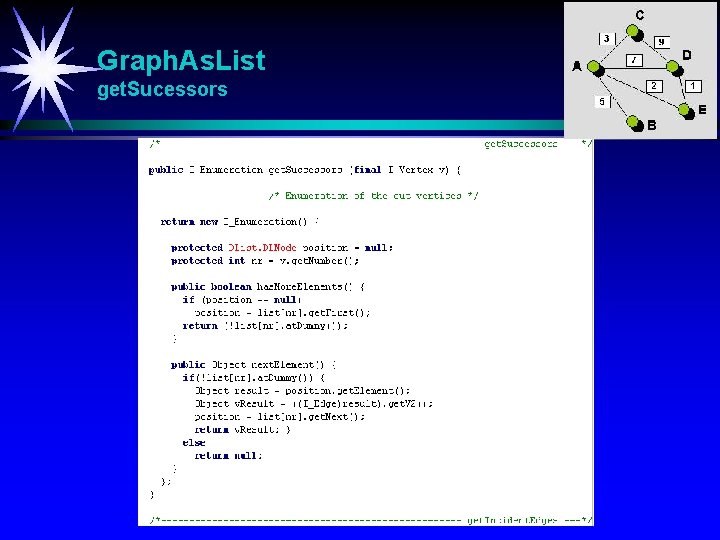
Graph. As. List get. Sucessors

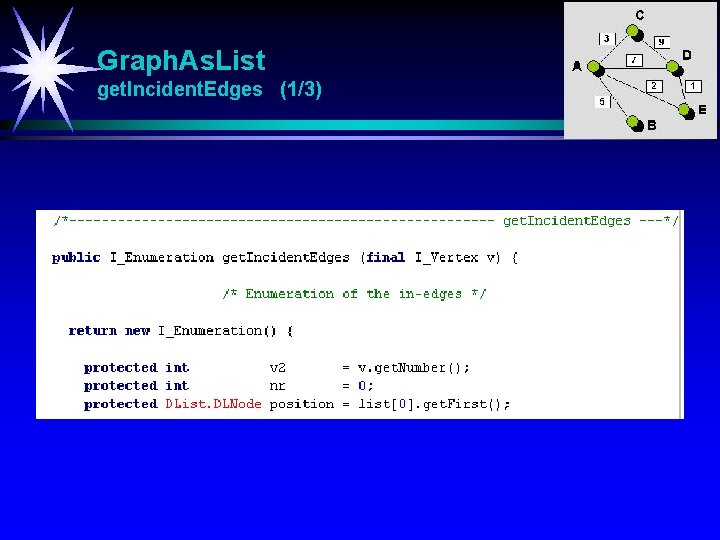
Graph. As. List get. Incident. Edges (1/3)

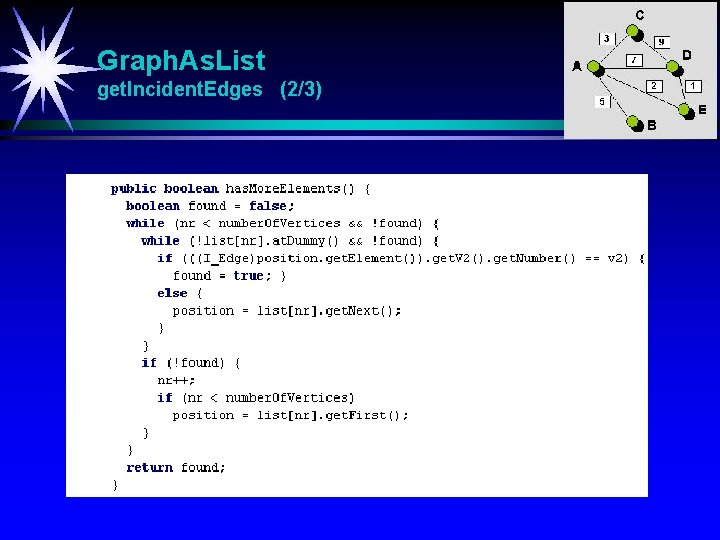
Graph. As. List get. Incident. Edges (2/3)

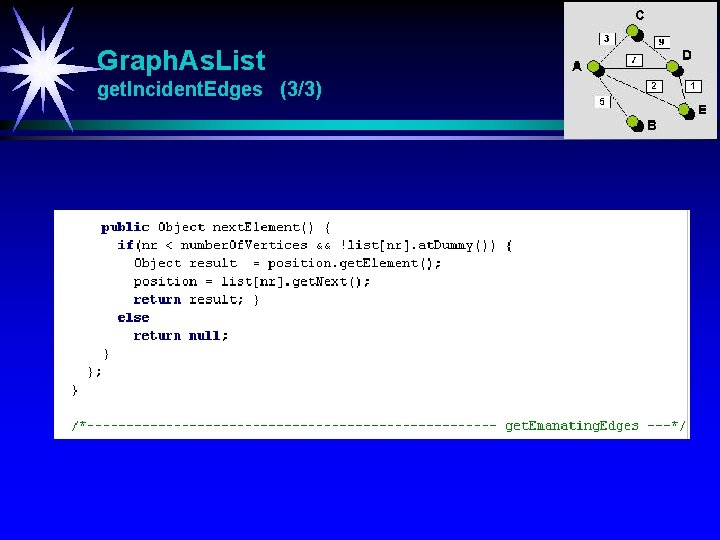
Graph. As. List get. Incident. Edges (3/3)

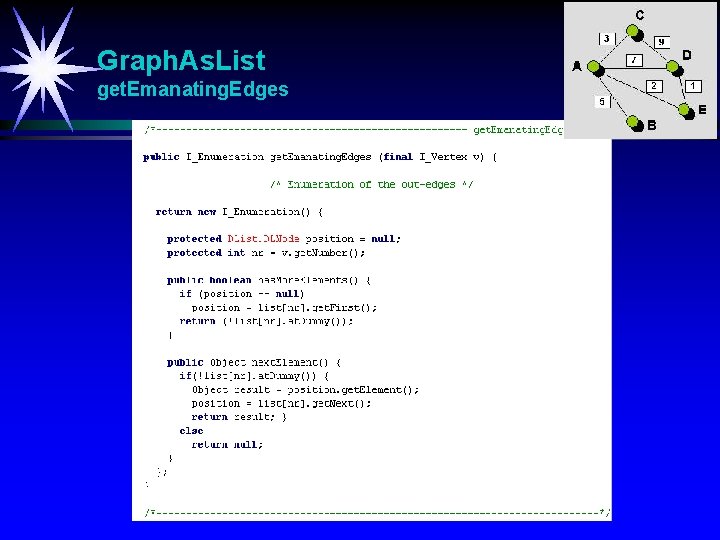
Graph. As. List get. Emanating. Edges

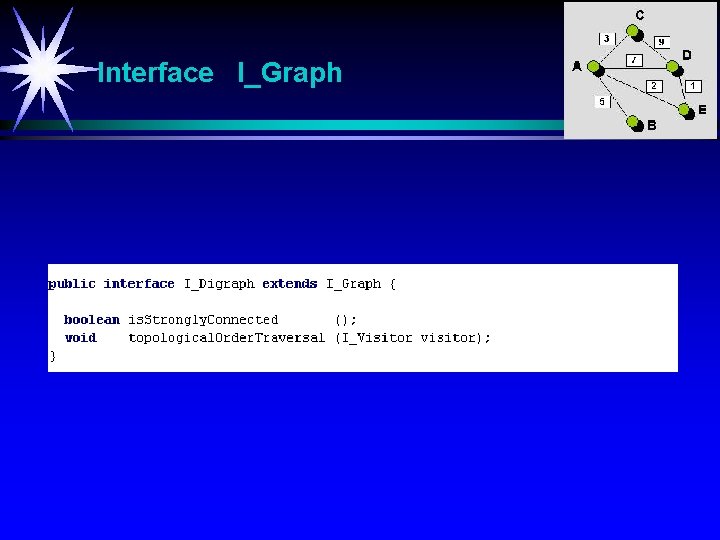
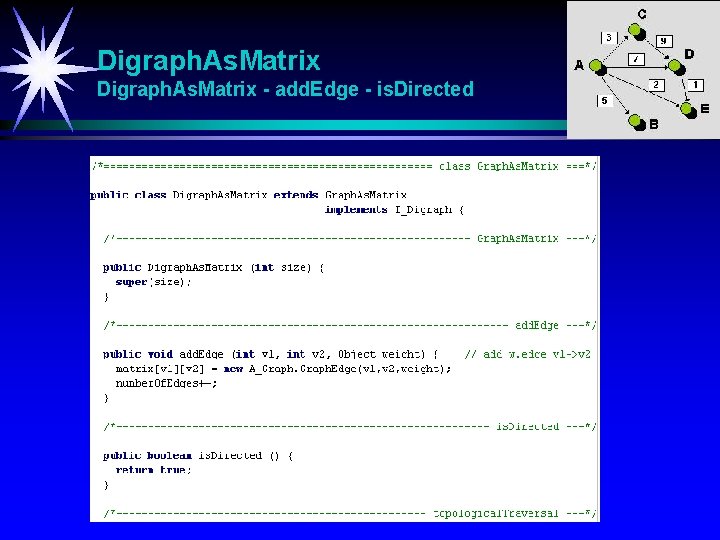
Digraph. As. Matrix - add. Edge - is. Directed

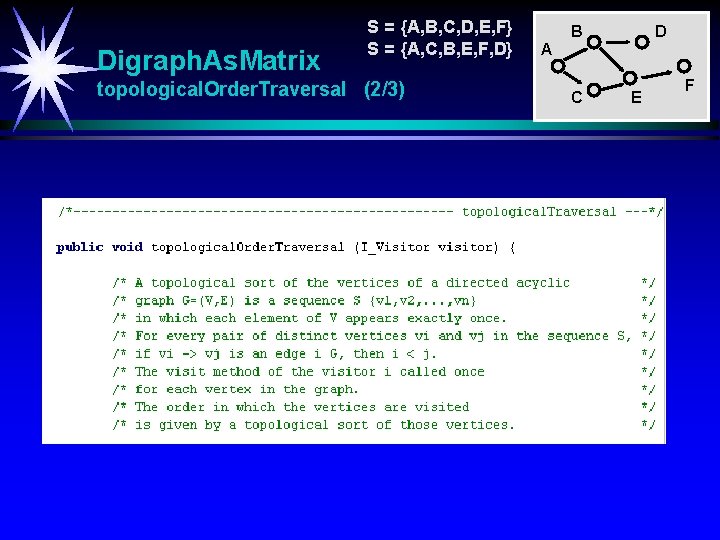
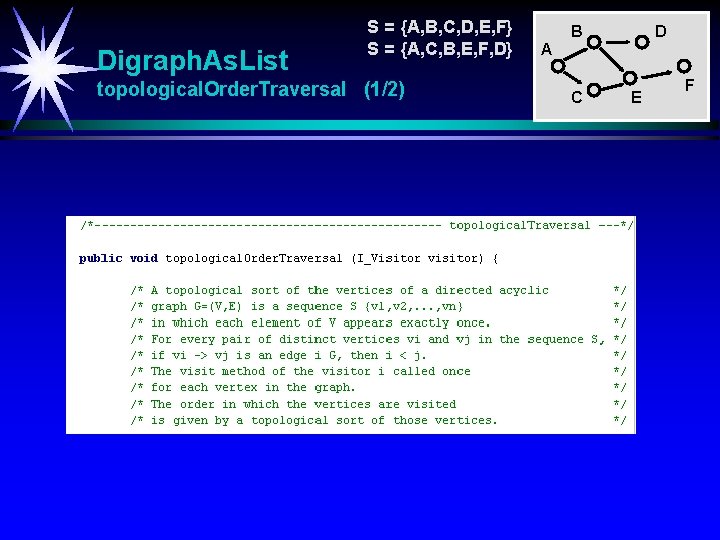
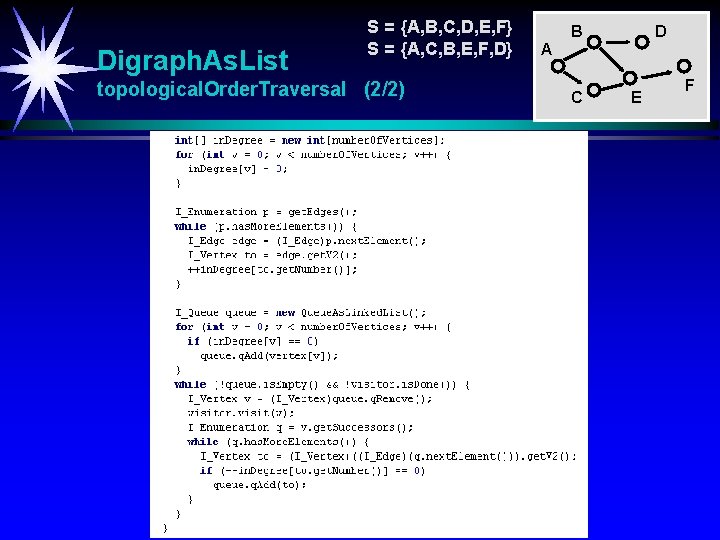
Digraph. As. Matrix S = {A, B, C, D, E, F} S = {A, C, B, E, F, D} topological. Order. Traversal (1/3) B D A C E F En topologisk sortering av en rettet, asyklisk graf er en sekvens S = {v 1, v 2, …vn} hvor alle noder er med eksakt en gang. For hvert par av distinkte noder vi og vj i S har vi i < j hvis det går en kant fra vi til vj. Strategi: WHILE flere noder velg en node med inngrad 0 (må finnes minst en slik hvis asyklisk graf) adder noden til sortering S slett noden og alle tilhørende utgående kanter fra grafen ENDWHILE Fjerning av en node og tilhørende utgående kanter kan simuleres ved å senke inngrad med 1 for alle etterfølgende noder.

Digraph. As. Matrix S = {A, B, C, D, E, F} S = {A, C, B, E, F, D} topological. Order. Traversal (2/3) B D A C E F

Digraph. As. Matrix S = {A, B, C, D, E, F} S = {A, C, B, E, F, D} topological. Order. Traversal (3/3) B D A C E F

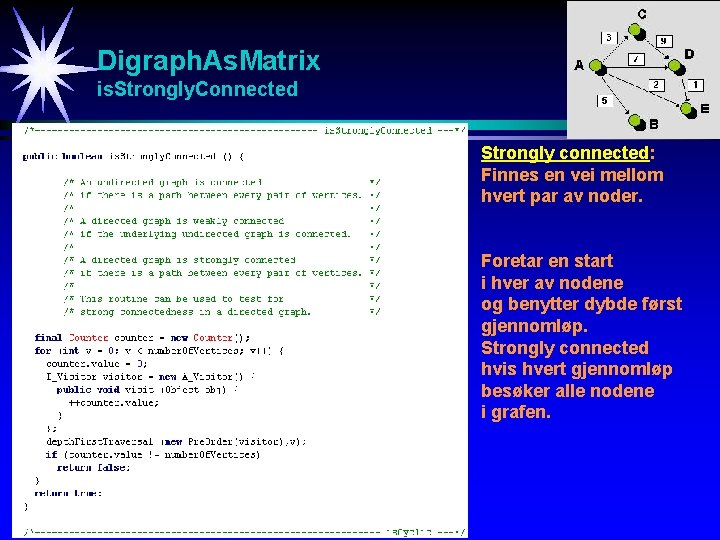
Digraph. As. Matrix is. Strongly. Connected Strongly connected: Finnes en vei mellom hvert par av noder. Foretar en start i hver av nodene og benytter dybde først gjennomløp. Strongly connected hvis hvert gjennomløp besøker alle nodene i grafen.

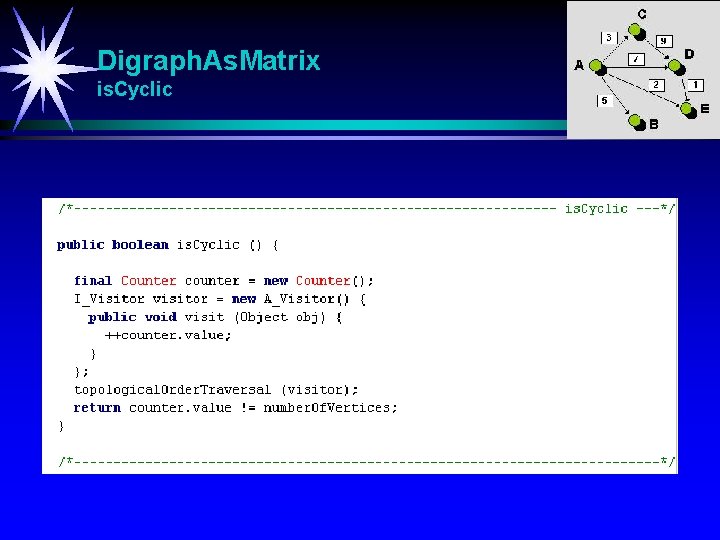
Digraph. As. Matrix is. Cyclic

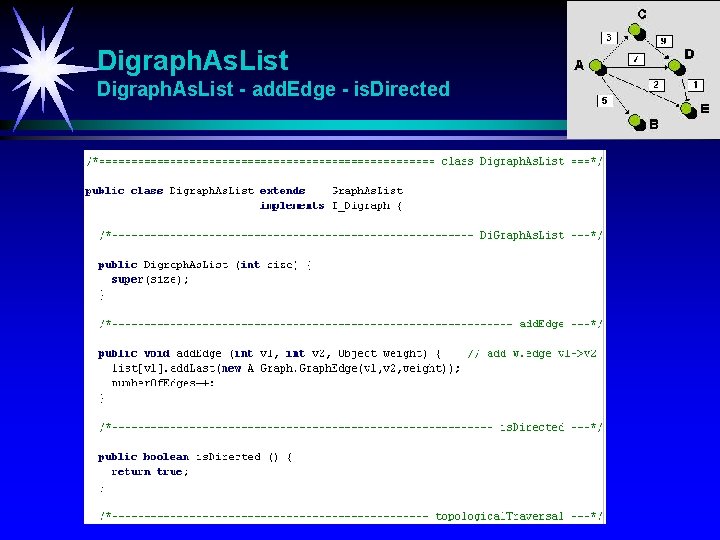
Digraph. As. List - add. Edge - is. Directed

Digraph. As. List S = {A, B, C, D, E, F} S = {A, C, B, E, F, D} topological. Order. Traversal (1/2) B D A C E F

Digraph. As. List S = {A, B, C, D, E, F} S = {A, C, B, E, F, D} topological. Order. Traversal (2/2) B D A C E F

Digraph. As. List is. Strongly. Connected

Digraph. As. List is. Cyclic

Test_Graph. As. Matrix (1/2)

Test_Graph. As. Matrix (2/2)

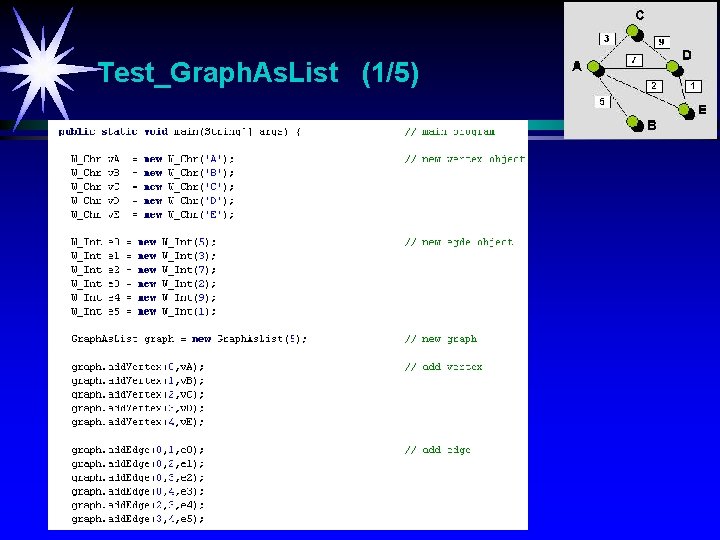
Test_Graph. As. List (1/5)

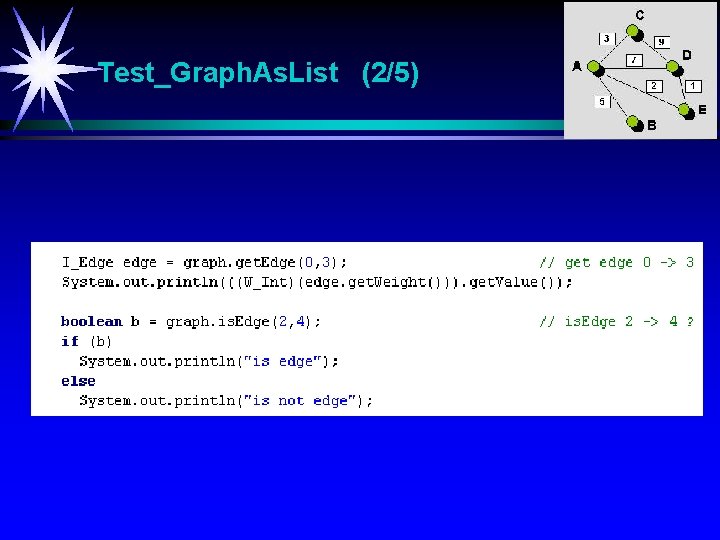
Test_Graph. As. List (2/5)

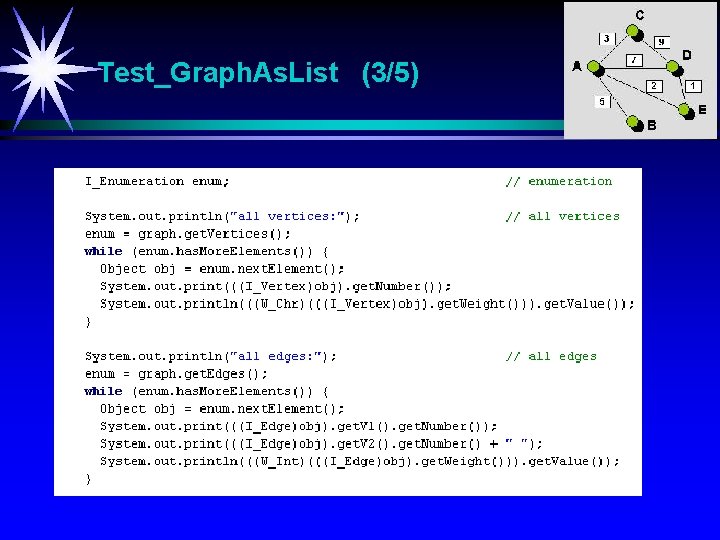
Test_Graph. As. List (3/5)

Test_Graph. As. List (4/5)

Test_Graph. As. List (5/5)

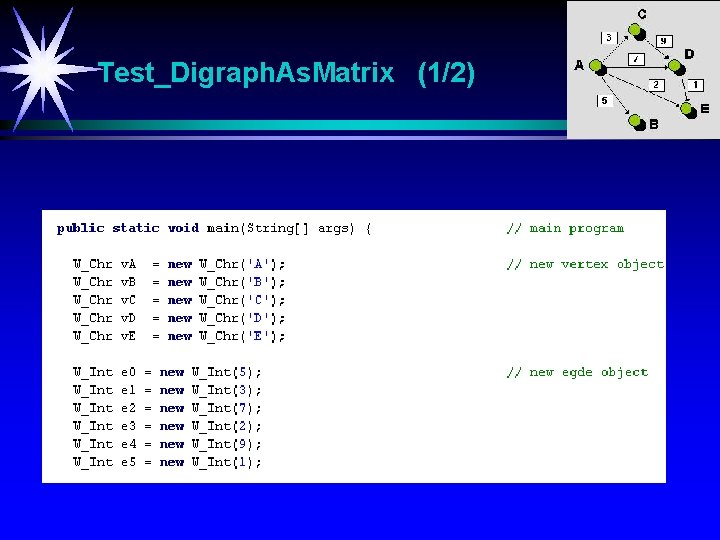
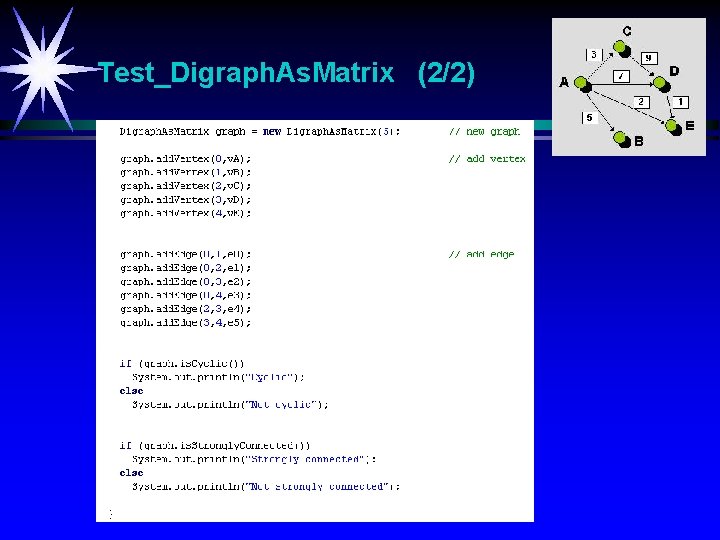
Test_Digraph. As. Matrix (1/2)

Test_Digraph. As. Matrix (2/2)

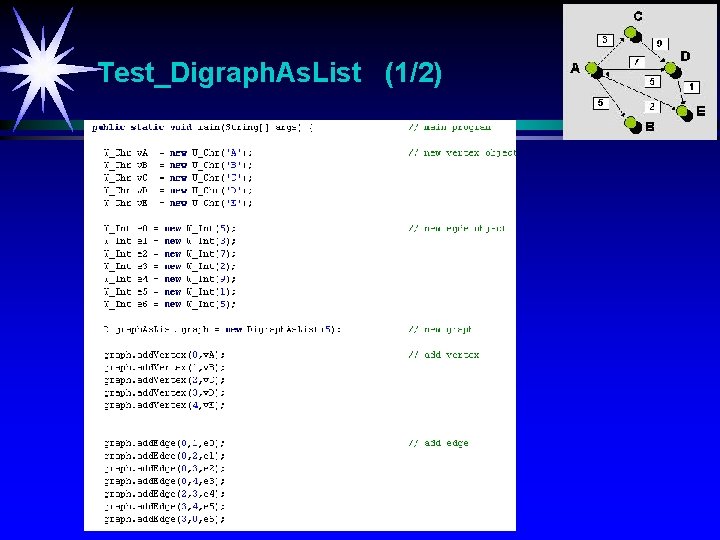
Test_Digraph. As. List (1/2)

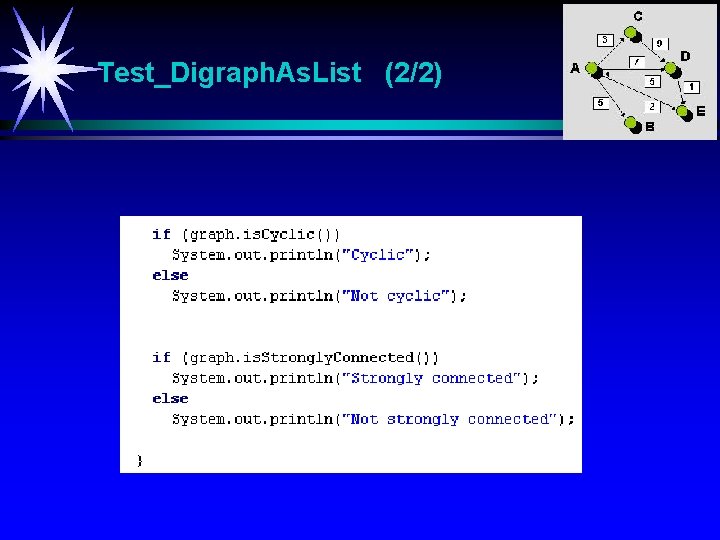
Test_Digraph. As. List (2/2)

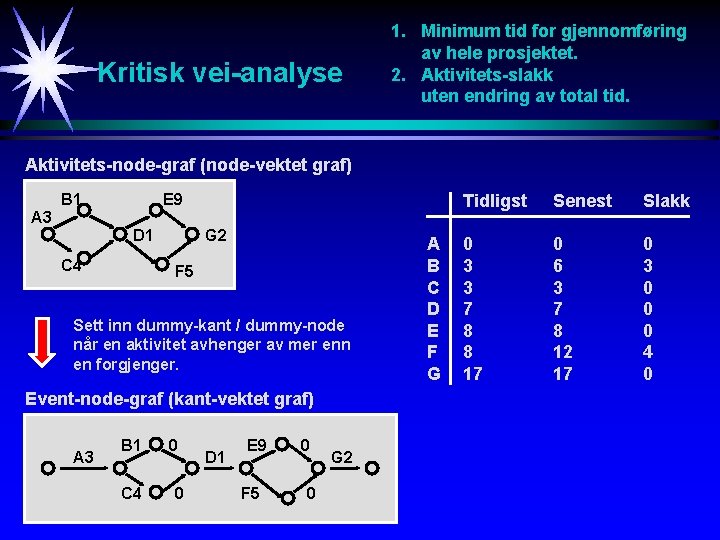
Kritisk vei-analyse 1. Minimum tid for gjennomføring av hele prosjektet. 2. Aktivitets-slakk uten endring av total tid. Aktivitets-node-graf (node-vektet graf) B 1 E 9 A 3 D 1 C 4 G 2 F 5 Sett inn dummy-kant / dummy-node når en aktivitet avhenger av mer enn en forgjenger. Event-node-graf (kant-vektet graf) A 3 B 1 C 4 0 0 D 1 E 9 F 5 0 0 G 2 A B C D E F G Tidligst Senest Slakk 0 3 3 7 8 8 17 0 6 3 7 8 12 17 0 3 0 0 0 4 0

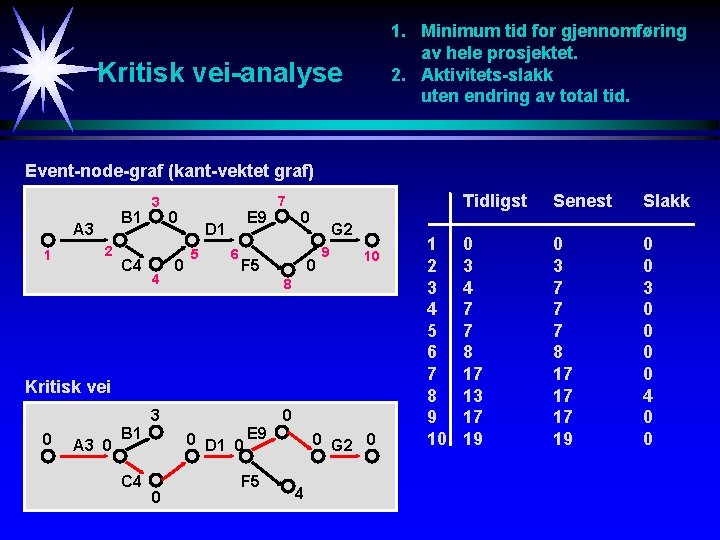
1. Minimum tid for gjennomføring av hele prosjektet. 2. Aktivitets-slakk uten endring av total tid. Kritisk vei-analyse Event-node-graf (kant-vektet graf) B 1 A 3 1 2 C 4 3 4 0 0 E 9 D 1 5 6 7 0 F 5 G 2 0 9 10 8 Kritisk vei 3 0 A 3 0 B 1 C 4 0 0 D 1 0 E 9 0 F 5 0 G 2 0 4 1 2 3 4 5 6 7 8 9 10 Tidligst Senest Slakk 0 3 4 7 7 8 17 13 17 19 0 3 7 7 7 8 17 17 17 19 0 0 3 0 0 4 0 0

3 0 Kritisk vei-analyse Earliest time: A 3 0 B 1 C 4 0 0 D 1 0 E 9 0 F 5 0 G 2 0 4 topological. Order. Traversal med Earliest. Time. Visitor Ev 1 C(v 1, w) Ew Evn C(vn, w) Latest time: reverse topological. Order: depth. First. Traversal med Post. Orden Latest. Time. Visitor Slack time: C(v 1, w) Lv 1 C(vn, w) Lvn Lw

END