Algoritmi paraleli pentru grafuri Algoritmi paraleli pentru grafuri

Algoritmi paraleli pentru grafuri

Algoritmi paraleli pentru grafuri • Arbori de acoperire minimi – Algoritmul lui Prim • Drumuri minime cu origine comuna – Algoritmul lui Dijkstra • Drumurile minime corespunzatoare tuturor perechilor de noduri – Algoritmul lui Dijkstra – Algoritmul lui Floyd • Maximal independent set – Algoritmul lui Luby

Algoritmul lui Prim - secvential Din: [Grama, Gupta, Kumar&Karypis]

Din: [Grama, Gupta, Kumar&Karypis]

Algoritmul lui Prim - paralel • Algoritmul contine un ciclu exterior cu n iteratii (liniile 8 -14). – Fiecare iteratie adauga un nou nod la arborele de acoperire minim. – Aceste iteratii nu pot fi executate in paralel – nu se poate selecta mai mult de un nod odata, pentru ca valorile d[v] se actualizeaza de fiecare data cand un nou nod u este adaugat la arborele de acoperire • Se paralelizeaza ciclul interior • p procese, n noduri. => se partitioneaza nodurile, fiecare procesor primeste n/p noduri • In fiecare pas, fiecare procesor selecteaza un minim local din segmentul d pe care il detine, apoi il transmite la P 0 unde se calculeaza u ca fiind minimul global dintre acestea (all-to-one reduction) • Nodul u se adauga la arbore, se transmite alegerea prin broadcast la toate procesoarele. Fiecare procesor isi actualizeaza distantele d[v], tinand cont de nodul u adaugat. • Procesorul care detine nodul v trebuie sa acceseze ponderea arcului (u, v) => fiecare proces detine coloanele din matricea de adiacenta corespunzatoare setului de noduri pe care le detine • Matricea de adiacente se partitioneaza 1 -D pe coloane la fel si vectorul d.

Din: [Grama, Gupta, Kumar&Karypis]

Algoritmul lui Prim – paralel: Evaluarea performantelor • Timpul pentru selectarea minimului: O(n/p + log p). • Timpul pentru o operatie de broadcast : O(log p). • Timpul pentru actualizarea locala a vectorului d: O(n/p). • Timpul paralel pentru o iteratie (un nod adaugat la arbore): O(n/p + log p). • Timpul total paralel: O(n 2/p + n log p).

Algoritmul lui Dijkstra - secvential Din: [Grama, Gupta, Kumar&Karypis]

Algoritmul lui Dijkstra - paralel • Similar cu algoritmul lui Prim in paralel • Matricea de adiacente este partitionata pe blocuri 1 D • Performanta paralela este identica cu cea determinata la algoritmul lui Prim

Drumurile minime intre toate perechile de noduri • Executa de n ori algoritmul lui Dijkstra de determinare a drumurilor minime cu origine comuna – cu fiecare nod ca sursa • Complexitatea secventiala: O(n 3). • Strategii de paralelizare: – source partitioned (partitionare a surselor): Fiecare procesor executa o rulare a algoritmului Dijkstra-secvential, avand alt nod ca sursa – source parallel(sursa in paralel): Fiecare nod e asignat unui set de procese si se utilizeaza formularea paralela a algoritmului Dijkstra

Algoritmul lui Dijkstra – Source Partitioned • Utilizeaza n procesoare, fiecare procesor Pi gaseste drumurile minime de la nodul vi la toate celelalte noduri, executand algoritmul lui Dijkstra in forma secventiala. • Presupune replicarea matricii de adiacente pe fiecare procesor • Nu se fac comunicatii interprocese. • Timpul paralel: O(n 2). • Algoritmul este cost-optimal: W=n*Tp=O(n 3) • Dezavantaj: nu poate folosi mai mult de n procesoare

Algoritmul lui Dijkstra Source Parallel • Fiecare dintre cele n probleme de drumuri minime cu origine unica este rezolvata in paralel => se pot folosi pana la n 2 procesoare • Se utilizeaza p > n procesoare, fiecare problema de drumuri minime cu origine unica este rezolvata utilizand p/n procesoare • Timpul paralel: • Cost optimal daca p = O(n 2/log n)

Algoritmul lui Floyd Distanta minima intre nodurile i si j este fie arcul direct fie trece printr-un nod k: Relatia trebuie calculata pentru toate perechile de noduri si pentru toti k = 1, n. Complexitatea seriala W=O(n 3).

Algoritmul lui Floyd - secvential Din: [Grama, Gupta, Kumar&Karypis]

Algoritmul lui Floyd – Paralel, 2 D • Matrice D(k) este impartita in p blocuri de dimensiune (n / √p) x (n / √p). • Fiecare procesor actualizeaza partea sa din matrice in fiecare iteratie Din: [Grama, Gupta, Kumar&Karypis]

Algoritmul lui Floyd – Paralel, 2 D • • • Pentru a calcula dl(, kr-1) procesorul Pi, j are nevoie de dl(, kk-1) si dk(, kr-1). In general, in iteratia k , fiecare din cele √p procese de pe linia k trimite valorile tuturor celor √p - 1 procese de pe coloana sa Similar, fiecare din cele √p procese de pe coloana k trimite valorile tuturor celor √p - 1 procese de pe aceeasi linie Din: [Grama, Gupta, Kumar&Karypis]

Algoritmul lui Floyd – Paralel, 2 D Din: [Grama, Gupta, Kumar&Karypis]

Algoritmul lui Floyd – Paralel, 2 D Evaluarea performantelor • In fiecare iteratie, procesele de pe linia k si coloana k fac o operatie de one-to-all broadcast pe coloanele/liniile lor. • Dimensiunea datelor difuzate m= n/√p elemente, • Timpul de comunicatie intr-o iteratie k: O((n log p)/ √p). • Calculele efectuate de un proces intr-o iteratie k: Θ(n 2/p). • Timpul de calcul paralel:

Algoritmul lui Floyd – Paralel, 2 D Evaluarea performantelor • Cost-optimal daca p=O(n 2 / log 2 n) • Functia de izoeficienta: O(p 1. 5 log 3 p). • Algoritmul paralel poate fi imbunatatit daca se elimina sincronizarea dupa fiecare iteratie

Algoritmul lui Floyd – 2 D Pipeline • Se elimina sincronizarea din linia 7 a algoritmului. • Un proces incepe calculele la iteratia k dupa ce a terminat calculele la iteratia (k-1) si a primit partile necesare din matricea Dk-1 • Procesul Pij in iteratia k: • daca a terminat calculele la iteratia (k-1) si are elemente de pe linia k, trimite partea lui din matricea Dk-1 proceselor Pi-1, j si Pi+1, j (in loc de broadcast pe coloana, trimite numai la vecini) • daca a terminat calculele la iteratia (k-1) si are elemente de pe coloana k, trimite partea lui din matricea Dk-1 proceselor Pi, j-1 si Pi, j+1 (in loc de broadcast pe linie, trimite numai la vecini) • Daca au sosit date Dk-1 de pe linie, le transmite mai departe pe linie in partea opusa de unde au sosit • Daca au sosit date Dk-1 de pe coloana, le transmite mai departe pe coloana in partea opusa de unde au sosit

Din: [Grama, Gupta, Kumar&Karypis]

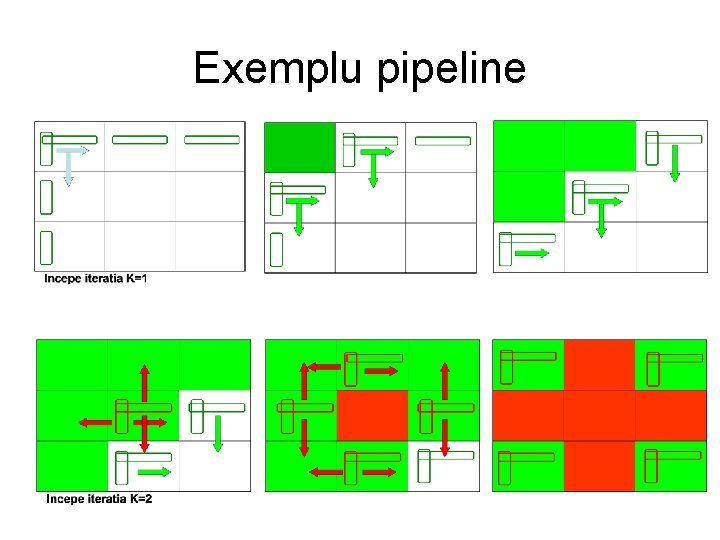
Exemplu pipeline

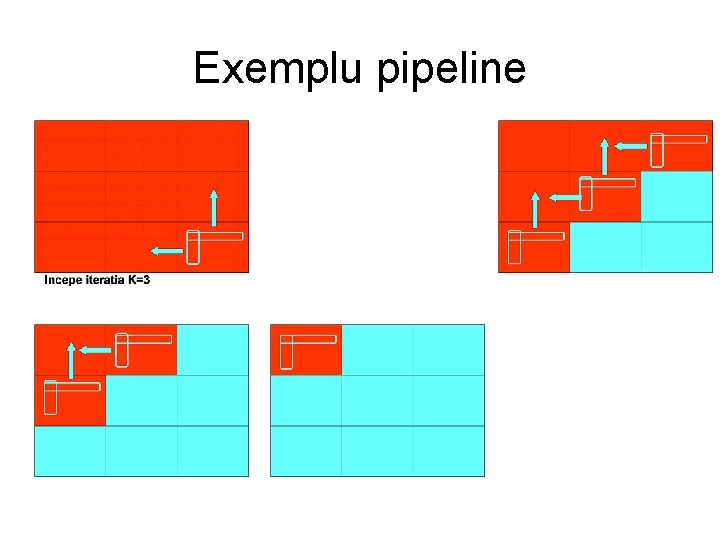
Exemplu pipeline

Algoritmul lui Floyd – Paralel Pipeline • Iteratia k=1: – In fiecare pas: • n/√p elemente de pe prima linie sunt trimise “in jos” de la un proces la altul • n/√p elemente de pe prima coloana sunt trimise “la dreapta” de la un proces la altul • Acest tip de comunicatii dureaza O(n/√p). – Dupa O(√p) pasi, procesul P√p , √p primeste elementele de pe prima linie si prima coloana -> dupa un timp O(n) • Pentru procesul P√p , √p valorile urmatoarelor linii si coloane (urmatoarele k iteratii) sosesc la intervale de timp de Θ(n 2/p) • Procesul P√p , √p termina calculele sale finale in timp Θ(n 3/p) + Θ(n). • Cand procesul P√p , √p termina iteratia k=(n-1), transmite segmentele din linia si coloana n pe care le detine la celelalte procese. Acestea ajung la P 0, 0 in timp O(n)

Algoritmul lui Floyd – Paralel Pipeline • Timpul de calcul paralel: • Cost-optimal pentru O(n 2) procesoare

Comparatie intre metodele de determinare in paralel a drumurilor minime corespunzatoare tuturor perechilor de noduri Din: [Grama, Gupta, Kumar&Karypis]

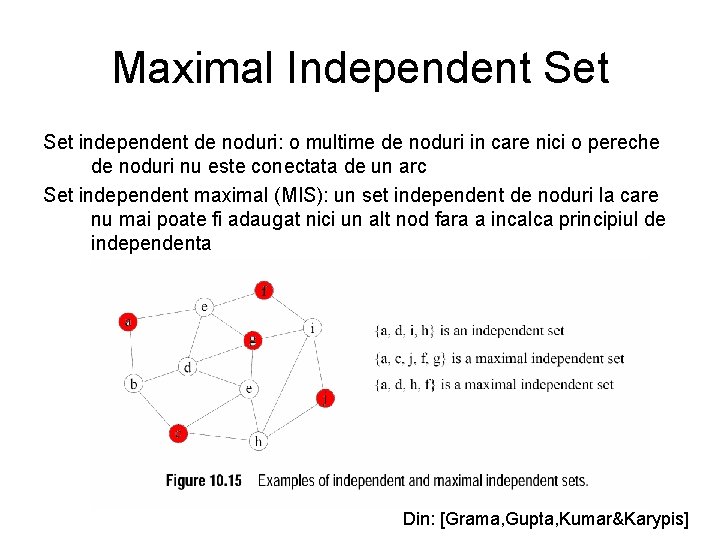
Maximal Independent Set independent de noduri: o multime de noduri in care nici o pereche de noduri nu este conectata de un arc Set independent maximal (MIS): un set independent de noduri la care nu mai poate fi adaugat nici un alt nod fara a incalca principiul de independenta Din: [Grama, Gupta, Kumar&Karypis]

Determinarea MIS Algoritm secvential: 1. 2. 3. 4. • • Initializeaza MIS cu multimea vida, initializeaza multimea nodurilor candidat C cu multimea nodurilor grafului Adauga un nod v din C la MIS Sterge toate nodurile adiacente lui v din C Repeta pasii 2 -3 pana cand multimea nodurilor candidat C ajunge vida Algoritmul acesta este intrinsec serial ! Punctul slab din punct de vedere al paralelizarii este pasul 2 – la o iteratie nu se poate trece mai mult de un nod din C in MIS

Determinarea MIS • Algoritm secvential paralelizabil: utilizeaza tehnica randomizarii pentru cresterea potentialului de concurenta (algoritmul lui Luby de colorare a grafurilor) 1. Initializeaza MIS cu multimea vida, initializeaza multimea nodurilor candidat C cu multimea nodurilor grafului 2. Genereaza si atribuie numere aleatoare unice fiecarui nod din C 3. Adauga la MIS toate nodurile v din C care au numarul aleator mai mic decat numarul tuturor vecinilor 4. Sterge din C toate nodurile adiacente nodurilor v trecute in MIS la pasul 3 5. Repeta pasii 2 -4 pana cand multimea nodurilor candidat C ajunge vida • • Nodurile care sunt selectate la pasul 3 si incluse in MIS sunt intradevar independente: daca nodul v a fost selectat, inseamna ca are numarul aleator cel mai mic dintre vecinii sai => nici un vecin de care este conectat prin arc nu mai este selectat in cadrul aceluiasi pas In medie, algoritmul va face O(log n ) iteratii.

Din: [Grama, Gupta, Kumar&Karypis]

Determinarea MIS - paralel • Paralelizarea: se partitioneaza multimea nodurilor candidat C la mai multe procese -> fiecare proces cauta in partitia sa noduri v care se trec la MIS. • Implementarile difera: – Memorie comuna – Comunicare prin mesaje