TIPURI SPECIALE DE GRAFURI CUPRINS 1 Graf complet

TIPURI SPECIALE DE GRAFURI

CUPRINS 1. Graf complet 2. Graf bipartit 3. Graf bipartit complet 4. Graf eulerian 5. Graf hamiltonian

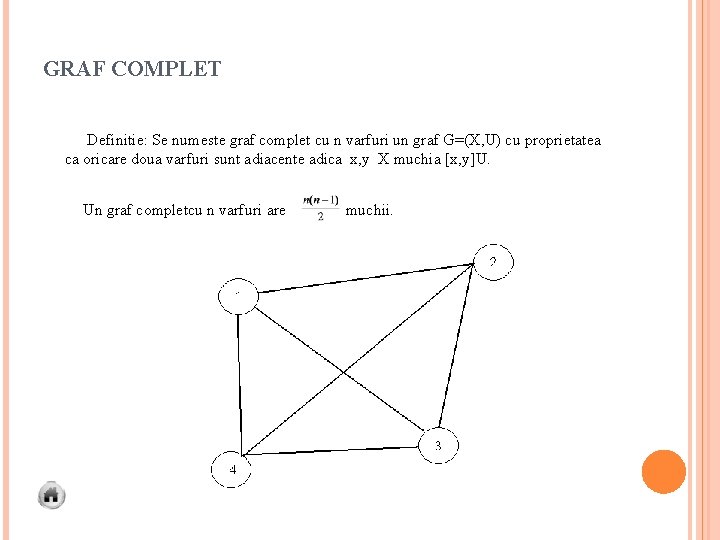
GRAF COMPLET Definitie: Se numeste graf complet cu n varfuri un graf G=(X, U) cu proprietatea ca oricare doua varfuri sunt adiacente adica x, y X muchia [x, y]U. Un graf completcu n varfuri are muchii.

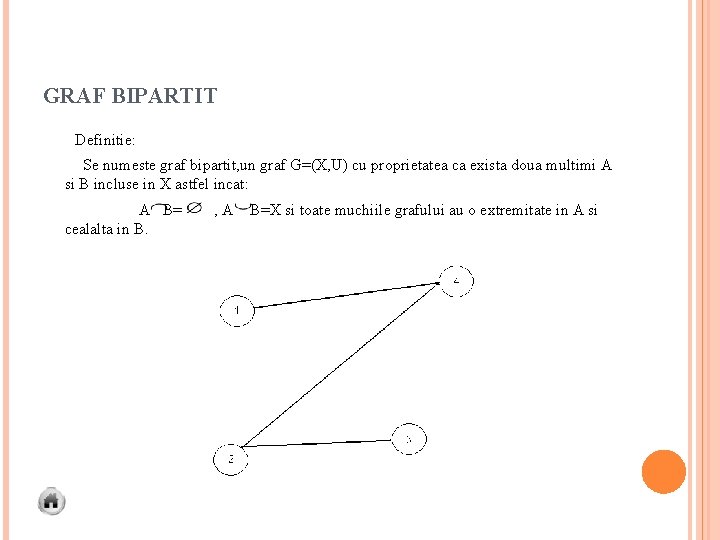
GRAF BIPARTIT Definitie: Se numeste graf bipartit, un graf G=(X, U) cu proprietatea ca exista doua multimi A si B incluse in X astfel incat: A B= , A B=X si toate muchiile grafului au o extremitate in A si cealalta in B.

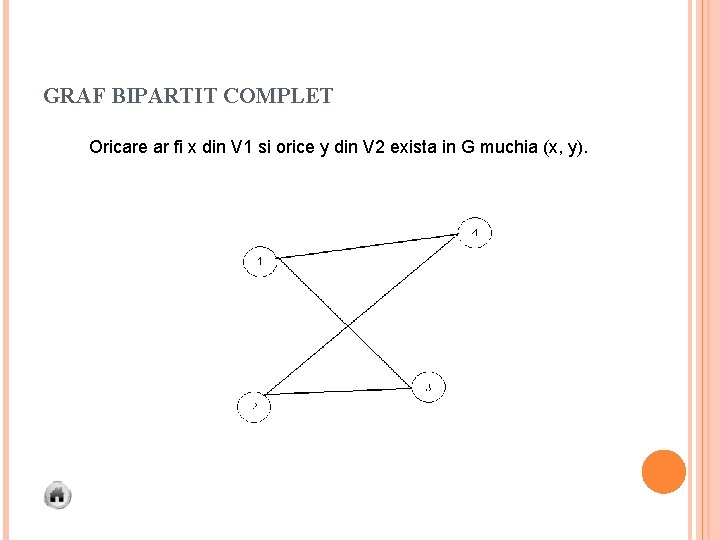
GRAF BIPARTIT COMPLET Oricare ar fi x din V 1 si orice y din V 2 exista in G muchia (x, y).

VERIFICARE DACA UN GRAF G ESTE BIPARTIT: #include<iostream. h> int a[20], i, j, k, m, n, viz[20], ca[20], cb[20]; void citire() {for(i=1; i<=n; i++) for(j=i+1; j<=n; j++) cin>>a[i][j]; } int verificare(int v[], int k) {for(i=1; i<=k-1; i++) if(a[v[i]][v[k]]==1) return 1 ; } int bipartit() {int pa=0, pb=0, ua=0, ub=0, ok=1; for(i=1; i<=n && ok==1; i++) if(viz[i]==0) {ca[++ua]=i; viz[i]=1; if(ua==1) pa=1; while(pa<=ua || pb<=ub&&ok==1) {while(pa<=ua) {x=ca[pa]; for(i=1; i<=n; i++) if(a[x][i]==1&&viz[i]==0) {cb[++ub]=i; if(ub==1) pb=1; if(!verificare (cb, ub)) ok=0; else viz[i]=2; } pa++; } while(pb<=ub &&ok==1) x=cb[pb]; for(i=1 i; i<=n; i++) if(a[x][i]==1&&viz[i]==0) {cb[++ua]=i;

if(ua==1) pa=1; if(!verificare(ca, ua)) ok=0; else viz[i]=1; } pb++; } }} return ok; } int main() {citire(); if(bipartit()) {for(i=1; i<=n; i++) if(viz[i]==1) cout<<i<<” “; cout<<endl; for(i=1; i<=n; i++) if(viz[i]==2) cout<<i<<” “; } else cout<<”nu este bipartit”; return 0 ; }

GRAF EULERIAN Definitie : Un graf este eulerian daca si numai daca este conex si gradele tuturor varfurilor sunt numere pare. Numim graf eulerian un graf care contine un ciclu eulerian. Numim ciclu eulerian un cilcu care contine toate muchiile. Fie graful din figura urmatoare: -se determina daca graful contine un ciclu eulerian (toate nodurile au grad par si este conex) -se retin gradele tuturor nodurilor in vectorul g. Acesta va retine: g=[2, 4, 4, 2] -ciclul se genereaza pas cu pas retinand nodurile intr-o lista gestionata de variabilele p si u (prima si ultima componenta) -se genereaza un ciclu pornind de la nodul 1 care se adauga in lista p (acesta va fi si u la inceput). In continuare se adauga noduri adiacente cu informatia retinuta de u si se continua astfel pana se ajunge iar la nodul 1. De fiecare data cand se adauga o muchie (u->info, i) la ciclu se micsoreaza gradul lui u->info si lui i iar muchiile (u->info, i) si (i, u->info) se elimina.

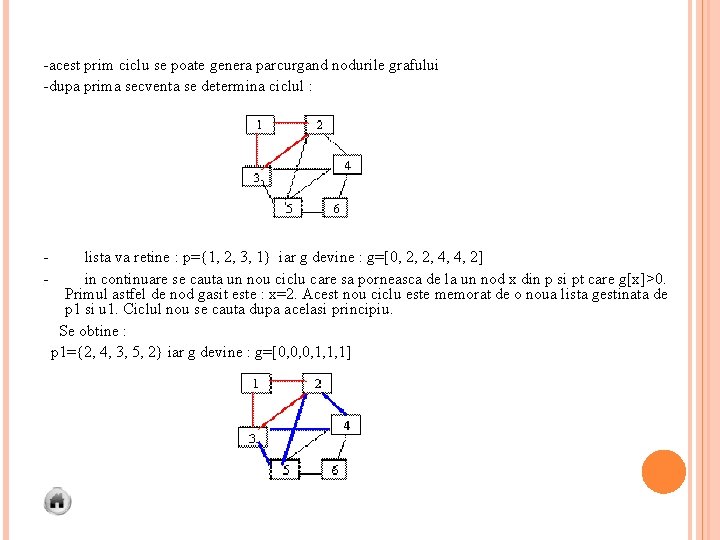
-acest prim ciclu se poate genera parcurgand nodurile grafului -dupa prima secventa se determina ciclul : - lista va retine : p={1, 2, 3, 1} iar g devine : g=[0, 2, 2, 4, 4, 2] - in continuare se cauta un nou ciclu care sa porneasca de la un nod x din p si pt care g[x]>0. Primul astfel de nod gasit este : x=2. Acest nou ciclu este memorat de o noua lista gestinata de p 1 si u 1. Ciclul nou se cauta dupa acelasi principiu. Se obtine : p 1={2, 4, 3, 5, 2} iar g devine : g=[0, 0, 0, 1, 1, 1]

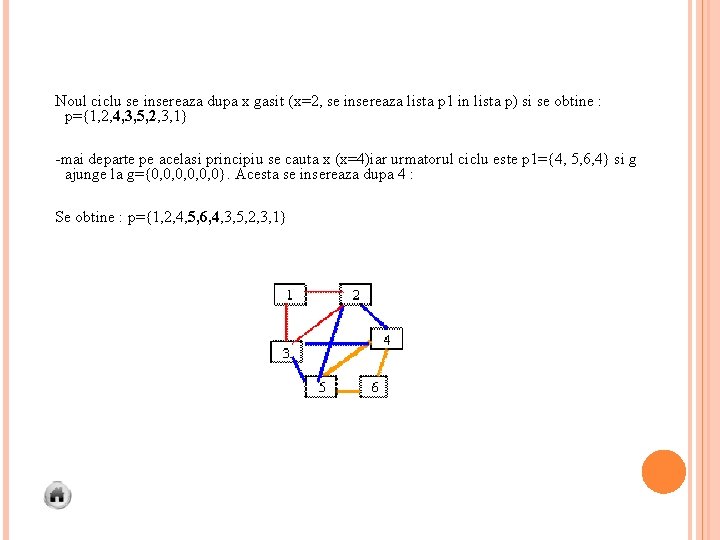
Noul ciclu se insereaza dupa x gasit (x=2, se insereaza lista p 1 in lista p) si se obtine : p={1, 2, 4, 3, 5, 2, 3, 1} -mai departe pe acelasi principiu se cauta x (x=4)iar urmatorul ciclu este p 1={4, 5, 6, 4} si g ajunge la g={0, 0, 0, 0}. Acesta se insereaza dupa 4 : Se obtine : p={1, 2, 4, 5, 6, 4, 3, 5, 2, 3, 1}

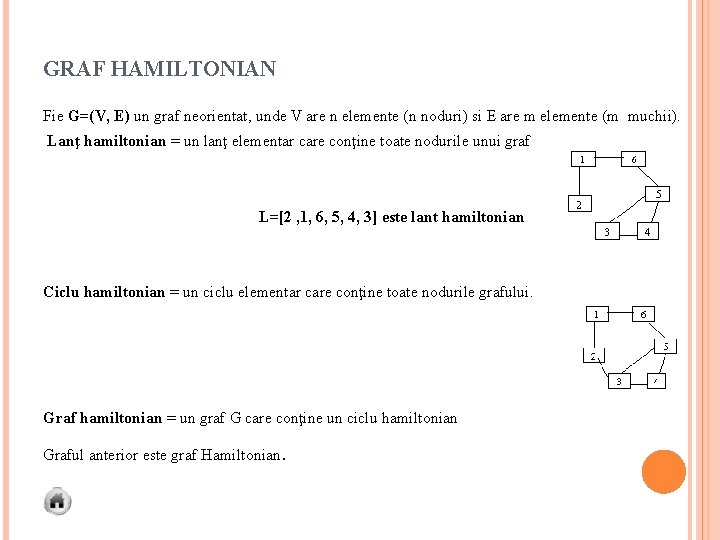
GRAF HAMILTONIAN Fie G=(V, E) un graf neorientat, unde V are n elemente (n noduri) si E are m elemente (m muchii). Lanţ hamiltonian = un lanţ elementar care conţine toate nodurile unui graf L=[2 , 1, 6, 5, 4, 3] este lant hamiltonian Ciclu hamiltonian = un ciclu elementar care conţine toate nodurile grafului. Graf hamiltonian = un graf G care conţine un ciclu hamiltonian Graful anterior este graf Hamiltonian .