DEFINISI GRAF ISTILAHISTILAH DALAM GRAF KETERHUBUNGAN Teori Graf

- DEFINISI GRAF - ISTILAH-ISTILAH DALAM GRAF - KETERHUBUNGAN Teori Graf Teknik Informatika Stt Wastukancana Purwakarta

GRAF? Pasangan himpunan (V, E) dimana V adalah himpunan tidak kosong dari vertices (simpul) = {v 1, v 2, v 3, . . . } dan E adalah himpunan edges (sisi) yang menghubungkan sepasang simpul {e 1, e 2, e 3, . . . } atau dapat ditulis dengan notasi G = (V, E)
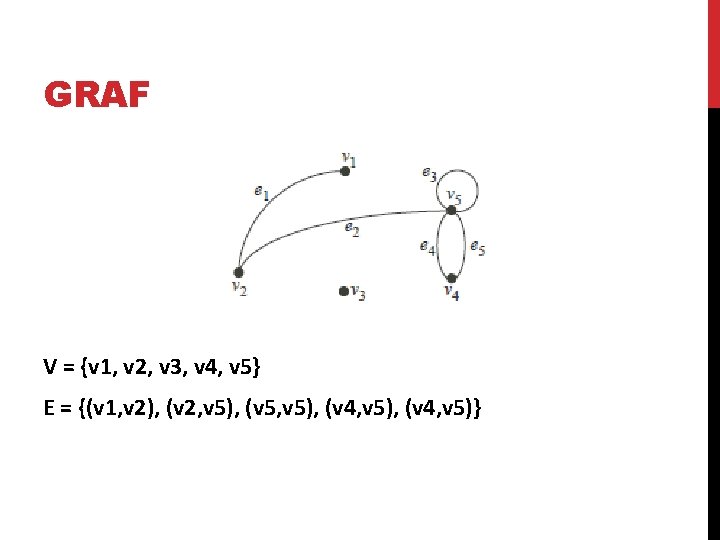
GRAF V = {v 1, v 2, v 3, v 4, v 5} E = {(v 1, v 2), (v 2, v 5), (v 5, v 5), (v 4, v 5)}

• Vertex u dan v adalah end vertex dari edge(u, v) • Edges yang memiliki end vertice yang sama adalah edge yang parallel • Sebuah edge (v, v) adalah loop • Graf sederhana (simple graph) tidak memiliki parallel edge atau loop • Graf yang tidak memiliki edge adalah graf kosong (empty graph) • Graf yang tidak memiliki vertex adalah graf nol (null graph) • Graf yang memiliki satu vertex adalah graf trivial • Edge dikatakan adjacent jika edge memiliki end vertex yang sama • Vertex u dan v dikatakan adjacent jika dihubungkan dengan sebuah egde

• Derajat (degree) dari vertex v, dinotasikan dengan d(v), adalah banyaknya edge yang memiliki end vertex v • Derajat dari sebuah loop dengan vertex v adalah dua • Pendant vertex adalah vertex yang memiliki degree 1 • Edge yang end vertex-nya berupa pendant vertex disebut pendant edge • Vertex dengan degree 0 adalah isolated vertex • Order adalah banyaknya vertex dalam suatu graf • Size adalah banyaknya edge dalamsuatu graf

DERAJAT (DEGREE)
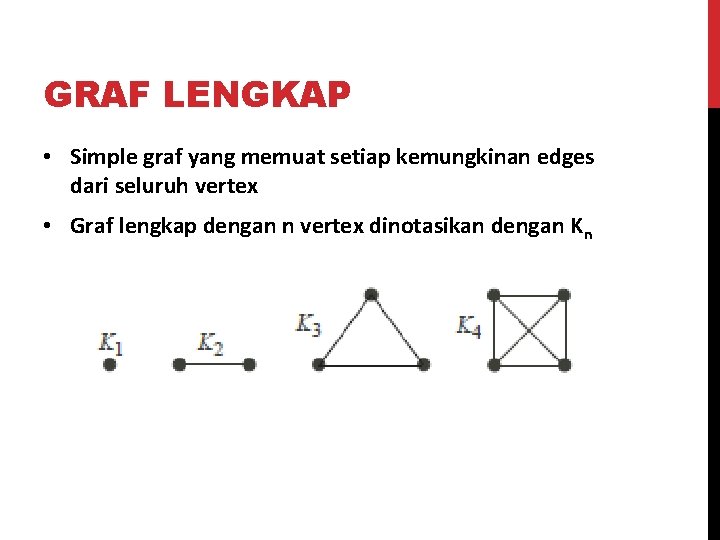
GRAF LENGKAP • Simple graf yang memuat setiap kemungkinan edges dari seluruh vertex • Graf lengkap dengan n vertex dinotasikan dengan Kn
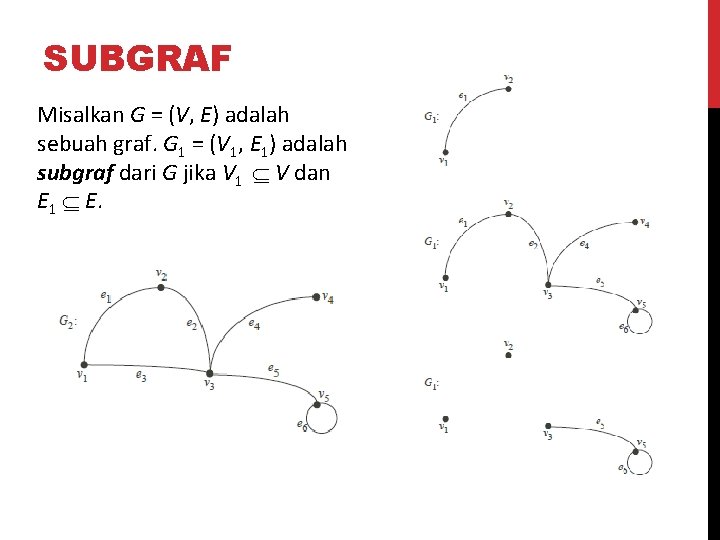
SUBGRAF Misalkan G = (V, E) adalah sebuah graf. G 1 = (V 1, E 1) adalah subgraf dari G jika V 1 V dan E 1 E.
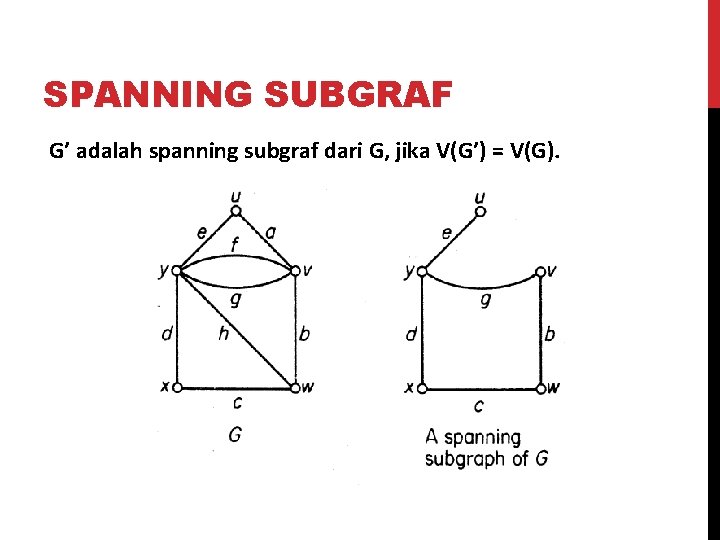
SPANNING SUBGRAF G’ adalah spanning subgraf dari G, jika V(G’) = V(G).

KETERHUBUNGAN (CONNECTION) • Walk : barisan vertex dan edge • Trail : walk dengan edge yang berbeda • Path : walk dengan vertex yang berbeda • Cycle / Circuit : trail tertutup dengan derajat setiap simpul = 2 • Jika v 1 disebut simpul awal, vn disebut simpul akhir. Sebuah walk disebut tertutup bila v 1 = vn , dalam hal lain walk disebut terbuka, yang menghubungkan v 1 dan vn • Path pasti trail, sedangkan trail belum tentu path

Walk terbuka : v 2, e 7, v 5, e 8, v 5, e 6, v 4, e 5, v 4, e 3, v 4 Walk tertutup : v 4, e 5, v 4, e 3, v 3, e 2, v 2, e 7, v 5, e 6, v 4 Trail : v 1, e 8, v 5, e 9, v 1, e 1, v 2, e 7, v 5, e 6, v 4, e 4, v 4 Path : v 2, e 7, v 5, e 6, v 4, e 3, v 3 Circuit : v 2, e 7, v 5, e 6, v 4, e 3, v 3, e 2, v 2
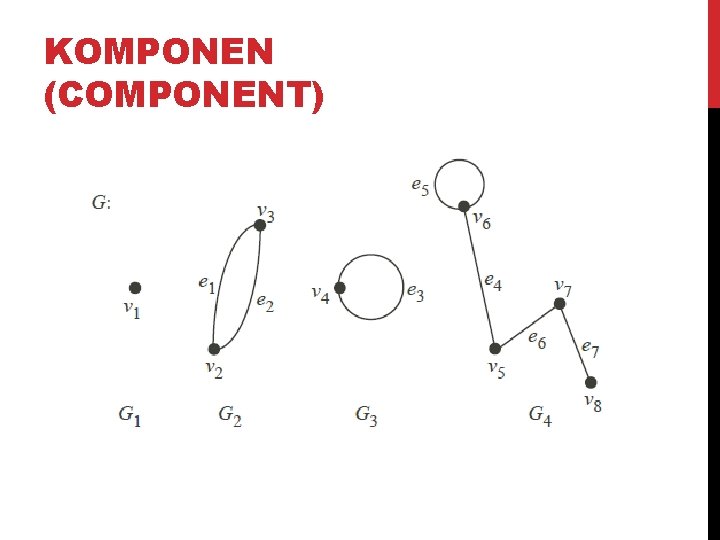
KOMPONEN (COMPONENT)
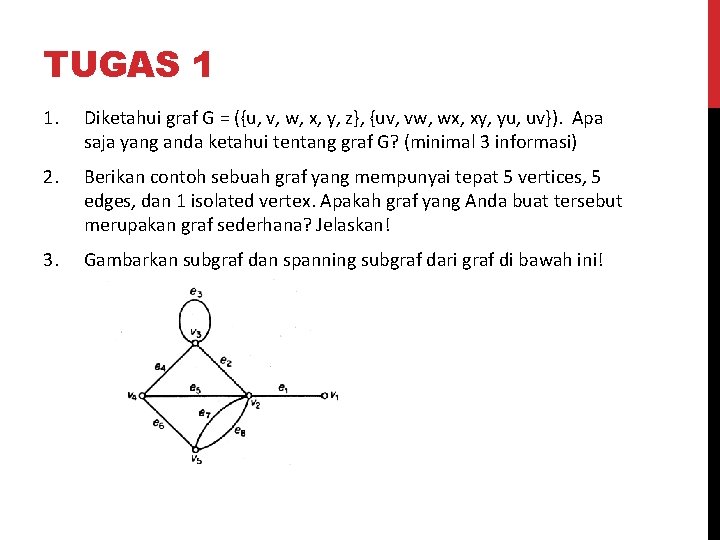
TUGAS 1 1. Diketahui graf G = ({u, v, w, x, y, z}, {uv, vw, wx, xy, yu, uv}). Apa saja yang anda ketahui tentang graf G? (minimal 3 informasi) 2. Berikan contoh sebuah graf yang mempunyai tepat 5 vertices, 5 edges, dan 1 isolated vertex. Apakah graf yang Anda buat tersebut merupakan graf sederhana? Jelaskan! 3. Gambarkan subgraf dan spanning subgraf dari graf di bawah ini!

4. Tuliskan derajat dari masing-masing vertex pada graf di bawah ini! 5. Berikan contoh walk, trail, path, dan circuit dari graf di bawah ini!
- Slides: 14