Structuri arborescente grafuri de tip arbore Structuri arborescente

Structuri arborescente (grafuri de tip arbore)

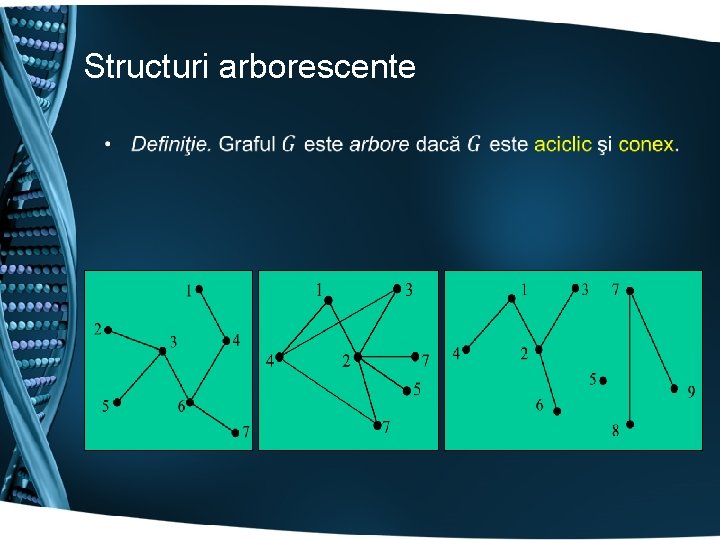
Structuri arborescente •

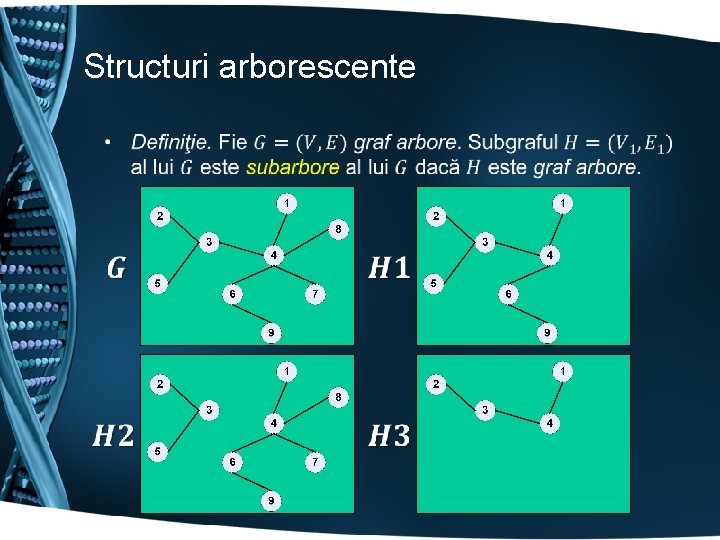
Structuri arborescente •

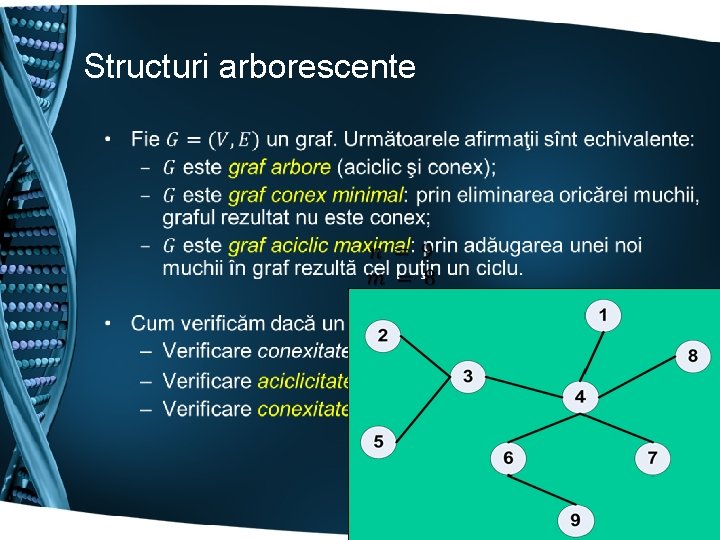
Structuri arborescente •

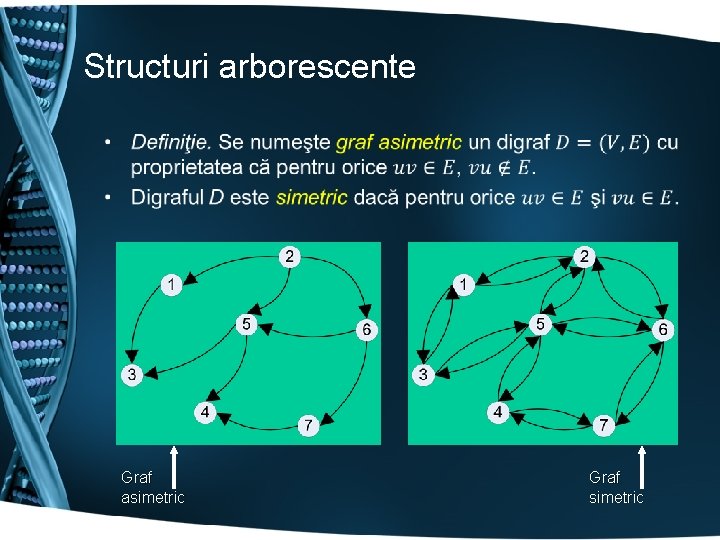
Structuri arborescente • Graf asimetric Graf simetric

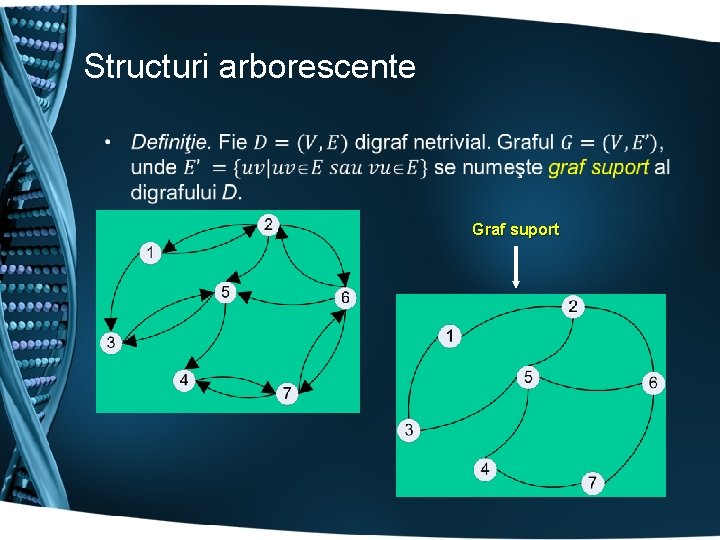
Structuri arborescente • Graf suport

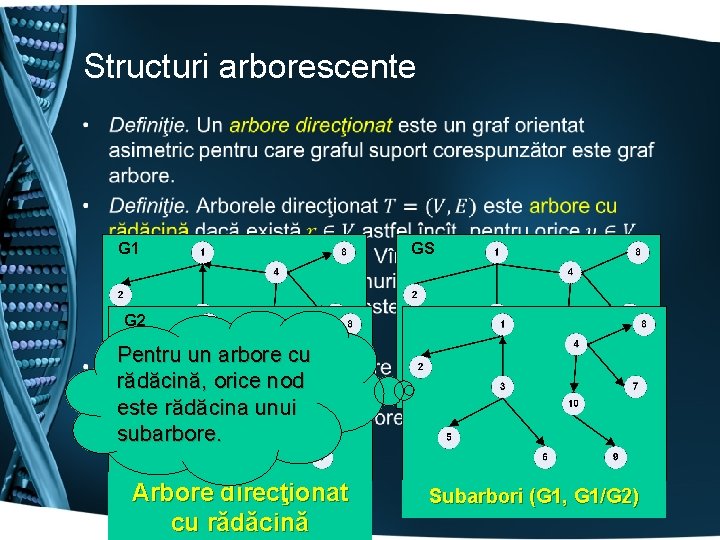
Structuri arborescente • G 1 GS G 2 Pentru un arbore cu rădăcină, orice nod este rădăcina unui Graf orientat asimetric Arbore direcţionat subarbore. Graf orientat asimetric Arbore direcţionat cu rădăcină Graf suport Subarbori (G 1, G 1/G 2)

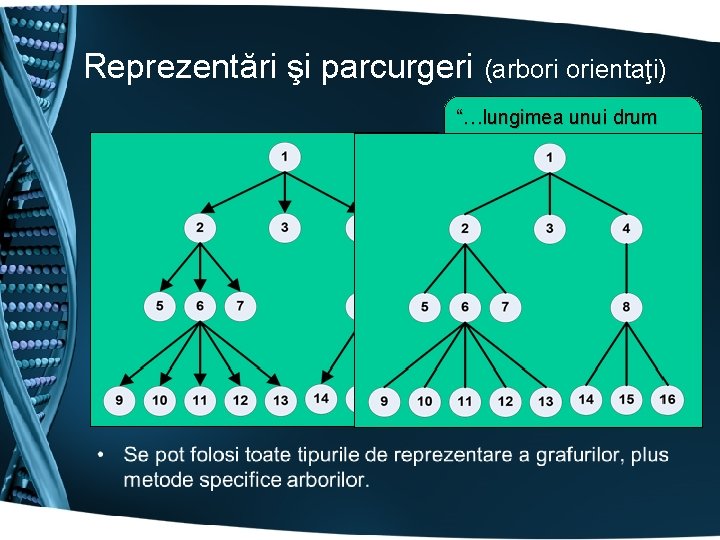
Reprezentări şi parcurgeri (arbori orientaţi) • “…lungimea unui drum este egală cu numărul de arce. ”

Reprezentarea Fiu-Frate • N: numărul de noduri din partea stîngă, conform reprezentării grafice • R: eticheta nodul rădăcină • FIU(i): eticheta primului descendent al vîrfului i Atenție la translația etichetă indice vector care urmează imediat lui i • FRATE(i): eticheta vîrfului descendent al tatălui vîrfului i şi spre dreapta, conform • INF(i): informaţia ataşată vîrfului i reprezentării grafice • adesea informaţia e chiar valoarea i, caz în care vectorul INF nu mai e necesar • Valoare lipsă (fiu, frate): se foloseşte o valoare convenţională (0, -1…)

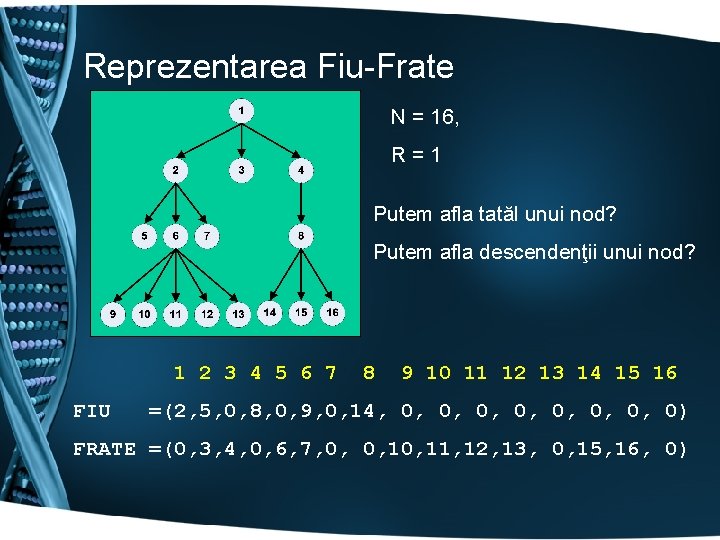
Reprezentarea Fiu-Frate N = 16, R = 1 Putem afla tatăl unui nod? Putem afla descendenţii unui nod? 1 2 3 4 5 6 7 FIU 8 9 10 11 12 13 14 15 16 =(2, 5, 0, 8, 0, 9, 0, 14, 0, 0, 0, 0) FRATE =(0, 3, 4, 0, 6, 7, 0, 0, 11, 12, 13, 0, 15, 16, 0)

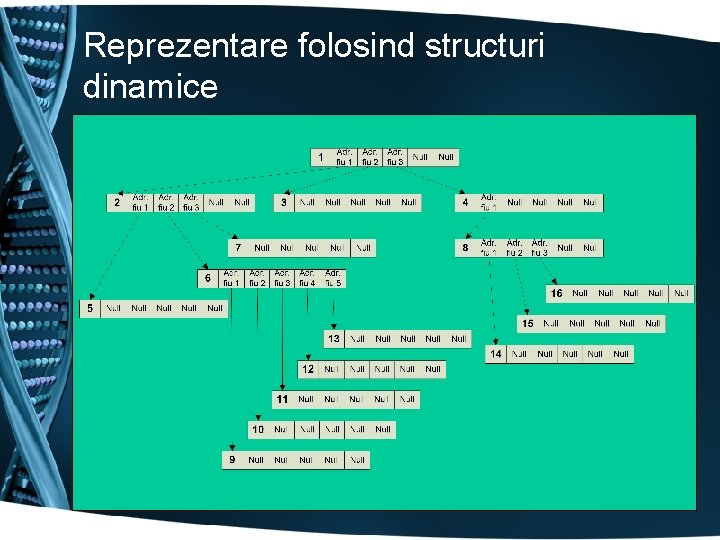
Reprezentare folosind structuri dinamice • Presupunînd că fiecare vîrf al arborelui are cel mult n descendenţi, fiecărui vîrf îi este asociată structura , vector de legături către descendenţii vîrfului identificator vîrf adresă fiu 1 … adresă fiu n

Parcurgeri • Aplicarea sistematică a unei reguli de vizitare a vîrfurilor arborelui. • Cele mai utilizate reguli de parcurgere a arborilor orientaţi sînt – A-preordine (variantă DF) – A-postordine (variantă DF) – parcurgerea pe niveluri (BF)

Parcurgerea în A-preordine (Fiu-Frate) • Se vizitează vîrful curent şi se identifică descendenţii lui. Se aplică aceeaşi regulă de vizitare pentru fiecare dintre arborii avînd ca rădăcini descendenţii vîrfului curent. void A_preordine (nod R) { if (R) { vizit (R); A_preordine(FIU[R]); A_preordine(FRATE[R]); } } 1, 2, 5, 6, 9, 10, 11, 12, 13, 7, 3, 4, 8, 14, 15, 16

Parcurgerea în A-postordine (Fiu-Frate) • Se identifică şi se vizitează descendenţii vîrfului curent, apoi se vizitează vîrful curent. Se aplică aceeaşi regulă de vizitare pentru arborii avînd ca rădăcini descendenţii vîrfului curent. void A_postordine (nod R) { if (R) { A_postordine(FIU[R]); vizit (R); A_postordine(FRATE[R]); } } 5, 9, 10, 11, 12, 13, 6, 7, 2, 3, 14, 15, 16, 8, 4, 1

Parcurgeri în adîncime (str. dinamice) void A_preordine (nod R) { if (R) { vizit (R); for(i=0; i<n; i++) A_preordine(R->leg[i]); } } void A_postordine (nod R) { if (R) { for(i=0; i<n; i++) A_postordine(R->leg[i]); vizit (R); } }

Parcurgerea pe niveluri (Fiu-Frate) void parcurgere_pe_niveluri(nod R, int FIU[], int FRATE[], int n) { TNOD* C = NULL; push(C, R); while (C) { pop(C, v); VIZIT(v); v=FIU[v]; while(v) { push(C, v); v=FRATE[v]; } } } 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16

Parcurgerea pe niveluri (str. dinamice) void parcurgere_pe_niveluri(nod *R) { TNOD* C = NULL; push(C, R); while (C) { pop(C, v); VIZIT(v); for(i=0; i<n; i++) if(R->leg[i]) push(C, R->leg[i]); } } 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16

Arbori parţiali •

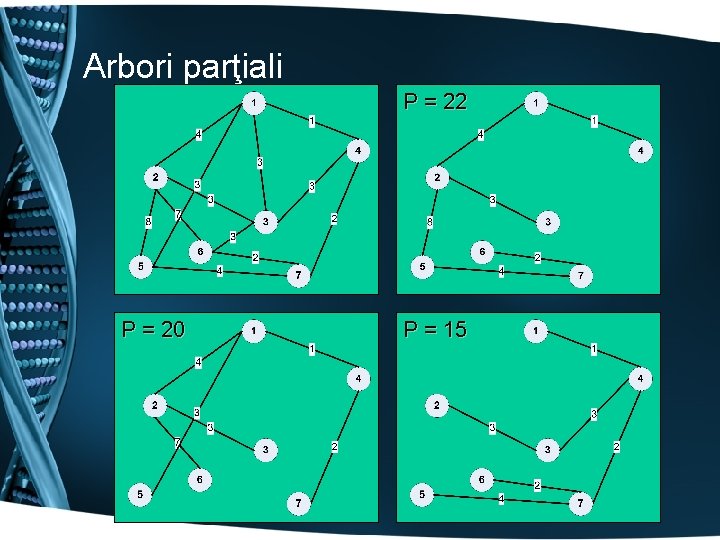
Arbori parţiali P = 22 P = 20 P = 15

Algoritmul lui Kruskal •

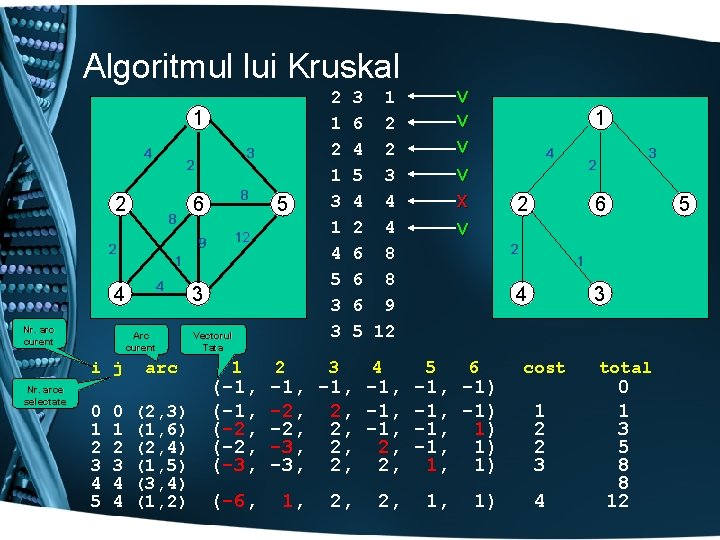
Algoritmul lui Kruskal 1 4 2 8 2 Nr. arce selectate 4 Arc curent i j 0 1 2 3 4 5 0 1 2 3 4 4 6 8 9 12 5 1 4 Nr. arc curent 3 2 arc (2, 3) (1, 6) (2, 4) (1, 5) (3, 4) (1, 2) 3 Vectorul Tata 1 (-1, (-2, (-3, (-6, 2 2 1 3 1 4 5 3 3 3 1 6 2 4 2 5 3 4 4 2 4 6 8 6 9 5 12 3 4 v v x v 1 4 2 2, 1 4 6 -1, -1, -1) -2, 2, -1, -1, 1) -3, 2, 2, 1, 1) 1, 6 2 5 1, 1) 3 2 3 cost 1 2 2 3 4 total 0 1 3 5 8 8 12 5

Algoritmul lui Kruskal • Funcţie pentru determinarea rădăcinii int radacina(int v, int tata[]) { int u = v; while(tata[u] >= 0) u = tata[u]; return u; } 1 2 Ex. : v = 4 (-6, 1, u = 4 tata[4]=2 u = 2 tata[2]=1 u = 1 tata[1]=-6 < 0 3 4 5 6 2, 1, 1)

Algoritmul lui Kruskal int kruskal(int a[][3], int nm, int nv, int b[][3]) { int tata[50], i, j, v 1, v 2, r 1, r 2; int c=0; for(i=0; i<nv; i++) tata[i]=-1; for(i=j=0; j<nv-1; i++) { v 1=a[i][0]; v 2=a[i][1]; r 1=radacina(v 1, tata); r 2=radacina(v 2, tata); if( r 1 != r 2 ) { if( tata[r 1] < tata[r 2] ) { tata[r 1]+=tata[r 2]; tata[r 2]=r 1; } else { tata[r 2]+=tata[r 1]; tata[r 1]=r 2; } b[j][0]=a[i][0]; b[j][1]=a[i][1]; b[j][2]=a[i][2]; c+=a[i][2]; j++; } } return c; }

Spor la învăţat!