Geomecnica computacional Mdulo 1 Geotecnia III UNLP Geomecnica


































- Slides: 70

Geomecánica computacional Módulo 1 Geotecnia III UNLP

Geomecánica Computacional 1 Terzaghi – Peck, Prólogo a la primera edición, 1948 2 “Desafortunadamente las actividades de investigación en mecánica de suelos. . . distrajeron la atención de muchos investigadores y docentes de las múltiples limitaciones impuestas por la naturaleza a la aplicación de la matemática a los problemas de ingeniería de tierras. . . En la inmensa mayoría de los casos no se necesita más que una predicción grosera, y si dicha predicción no puede ser realizada con medios simples, no puede ser realizada en absoluto” (Terzaghi 1948)

Geomecánica Computacional 1 Terzaghi – Peck, Prólogo a la tercera edición, 1996 3 “En el medio siglo que transcurrió. . . la investigación. . . ha permanecido inalterada, y se ha acumulado una vasta literatura referida a las propiedades de los suelos. . . Por lo tanto, hoy puede no ser cierto que si una predicción no puede ser realizada con medios simples, no puede ser realizada en absoluto. Como contrapartida de este progreso, es cada vez más importante que la elección de las propiedades de los suelos usadas en el análisis esté basada en un conocimiento fundamentalmente correcto del comportamiento de los suelos” (Peck 1996)

Geomecánica Computacional 1 Geomecánica computacional 4 Mecánica computacional: Simulación del comportamiento mecánico de materiales mediante técnicas computacionales Geomecánica computacional: Mecánica computacional aplicada a geomateriales En ingeniería civil • Suelos • Rocas • Hormigones • Materiales pulverulentos (cementos, etc. )

Geomecánica Computacional 1 Geomecánica computacional Geotecnia: resistencia de materiales – – Geotecnia Geomecánica Computacional: mecánica del continuo – – 5 muchas hipótesis simplificativas sobre materiales y geometría fórmulas analíticas “universales” menos hipótesis sobre materiales y G. Computacional geometría resultados numéricos válidos caso a caso

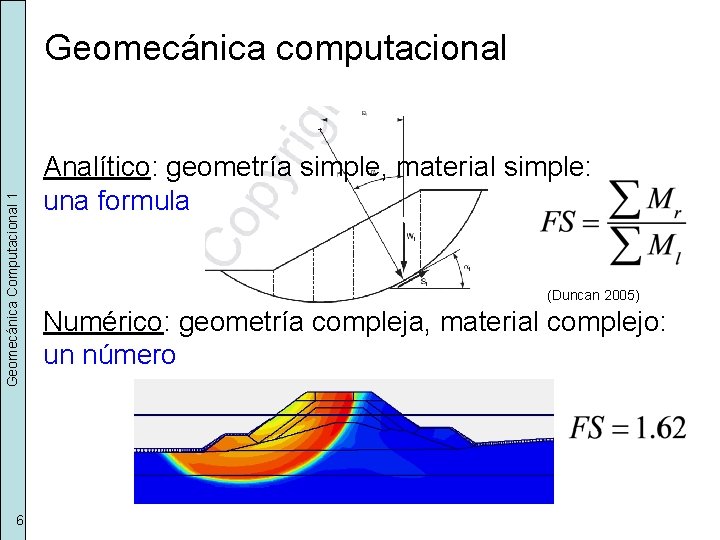
Geomecánica Computacional 1 Geomecánica computacional 6 Analítico: geometría simple, material simple: una formula (Duncan 2005) Numérico: geometría compleja, material complejo: un número

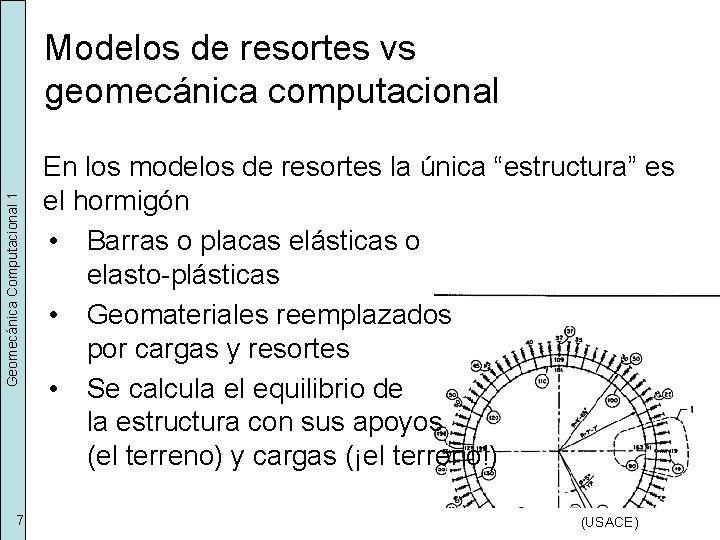
Geomecánica Computacional 1 Modelos de resortes vs geomecánica computacional 7 En los modelos de resortes la única “estructura” es el hormigón • Barras o placas elásticas o elasto-plásticas • Geomateriales reemplazados por cargas y resortes • Se calcula el equilibrio de la estructura con sus apoyos (el terreno) y cargas (¡el terreno!) (USACE)

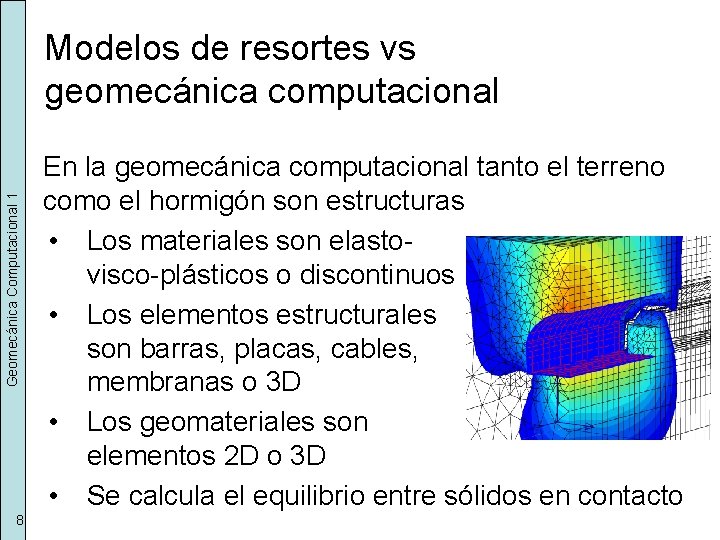
Geomecánica Computacional 1 Modelos de resortes vs geomecánica computacional 8 En la geomecánica computacional tanto el terreno como el hormigón son estructuras • Los materiales son elastovisco-plásticos o discontinuos • Los elementos estructurales son barras, placas, cables, membranas o 3 D • Los geomateriales son elementos 2 D o 3 D • Se calcula el equilibrio entre sólidos en contacto

Geomecánica Computacional 1 Ecuaciones constitutivas • El equilibrio relaciona fuerzas con tensiones (son las mismas para cualquier material) Fuerza Tensión Deformación Desplazamiento 9

Geomecánica Computacional 1 Ecuaciones constitutivas • El equilibrio relaciona fuerzas con tensiones • La cinemática relaciona deformaciones con desplazamientos (son las mismas para cualquier material) Fuerza Tensión Deformación Desplazamiento 10

Geomecánica Computacional 1 Ecuaciones constitutivas • El equilibrio relaciona fuerzas con tensiones • La cinemática relaciona deformaciones con desplazamientos • Las ecuaciones constitutivas relacionan tensiones con deformaciones (dependen del material que se estudia) – Sólido elástico… – Fluido Newtoniano… – Gas perfecto… Fuerza Tensión Deformación Desplazamiento 11

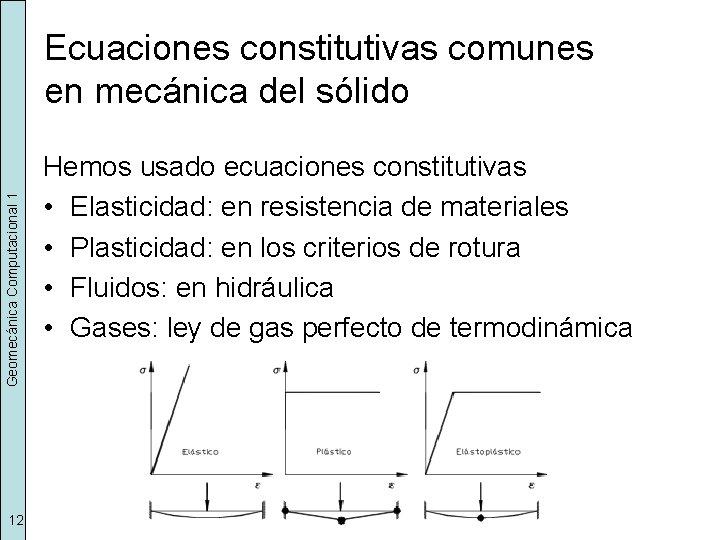
Geomecánica Computacional 1 Ecuaciones constitutivas comunes en mecánica del sólido 12 Hemos usado ecuaciones constitutivas • Elasticidad: en resistencia de materiales • Plasticidad: en los criterios de rotura • Fluidos: en hidráulica • Gases: ley de gas perfecto de termodinámica

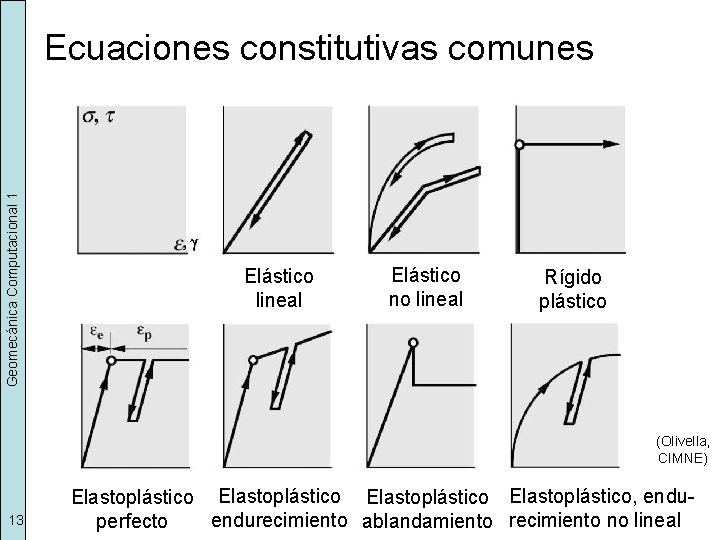
Geomecánica Computacional 1 Ecuaciones constitutivas comunes Elástico lineal Elástico no lineal Rígido plástico (Olivella, CIMNE) 13 Elastoplástico, endurecimiento ablandamiento recimiento no lineal perfecto

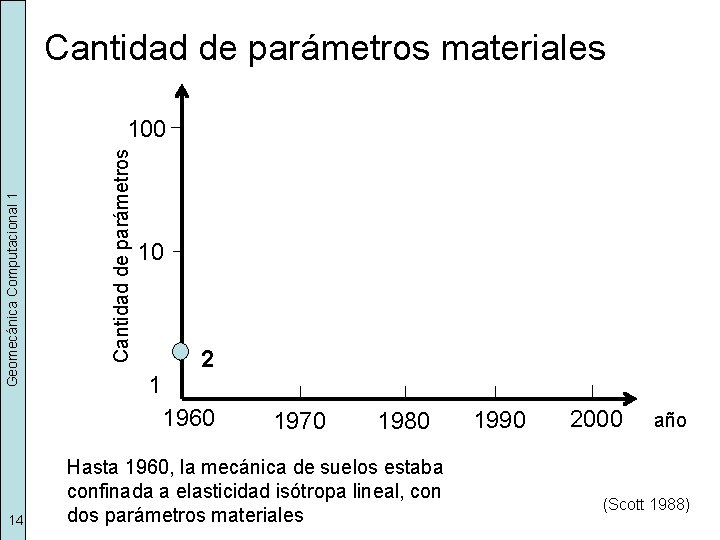
Cantidad de parámetros materiales Cantidad de parámetros Geomecánica Computacional 1 100 10 1 2 1960 14 1970 1980 Hasta 1960, la mecánica de suelos estaba confinada a elasticidad isótropa lineal, con dos parámetros materiales 1990 2000 año (Scott 1988)

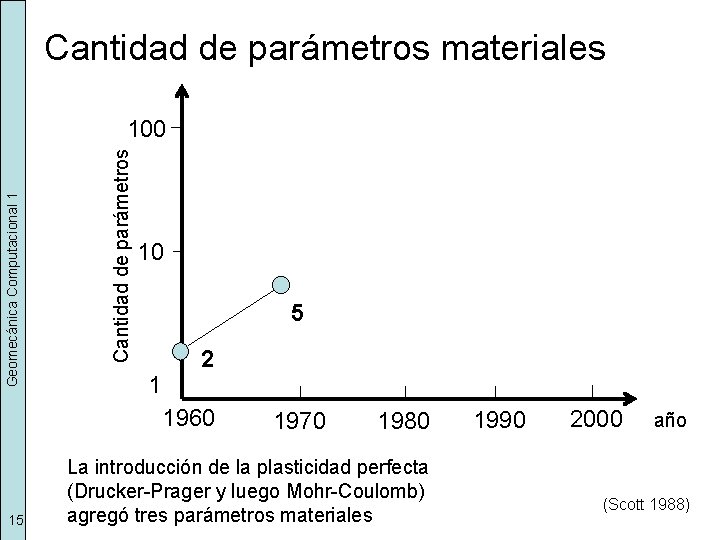
Cantidad de parámetros materiales Cantidad de parámetros Geomecánica Computacional 1 100 10 5 1 2 1960 15 1970 1980 La introducción de la plasticidad perfecta (Drucker-Prager y luego Mohr-Coulomb) agregó tres parámetros materiales 1990 2000 año (Scott 1988)

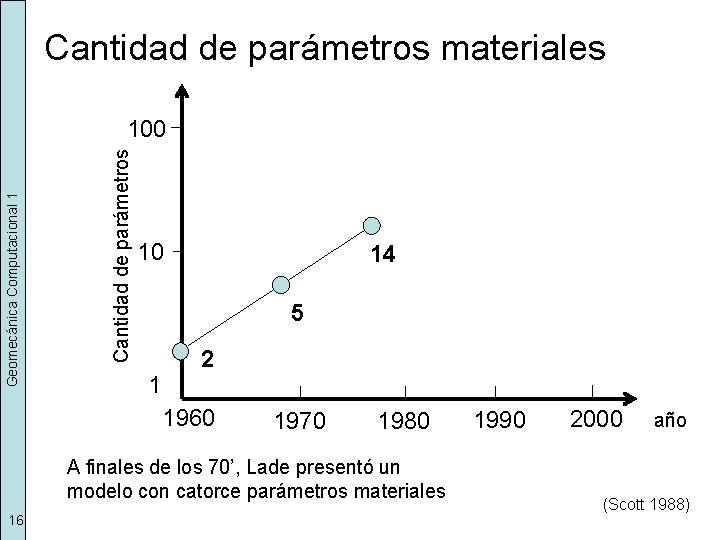
Cantidad de parámetros materiales Cantidad de parámetros Geomecánica Computacional 1 100 10 14 5 1 2 1960 1970 1980 A finales de los 70’, Lade presentó un modelo con catorce parámetros materiales 16 1990 2000 año (Scott 1988)

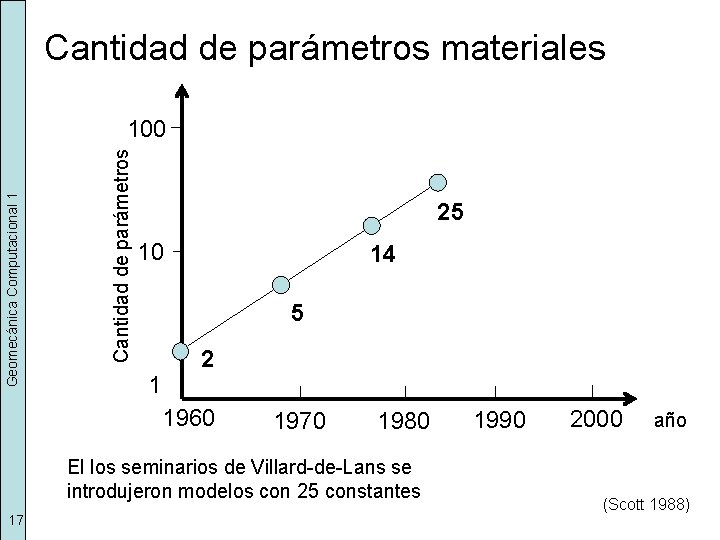
Cantidad de parámetros materiales Cantidad de parámetros Geomecánica Computacional 1 100 25 10 14 5 1 2 1960 1970 1980 El los seminarios de Villard-de-Lans se introdujeron modelos con 25 constantes 17 1990 2000 año (Scott 1988)

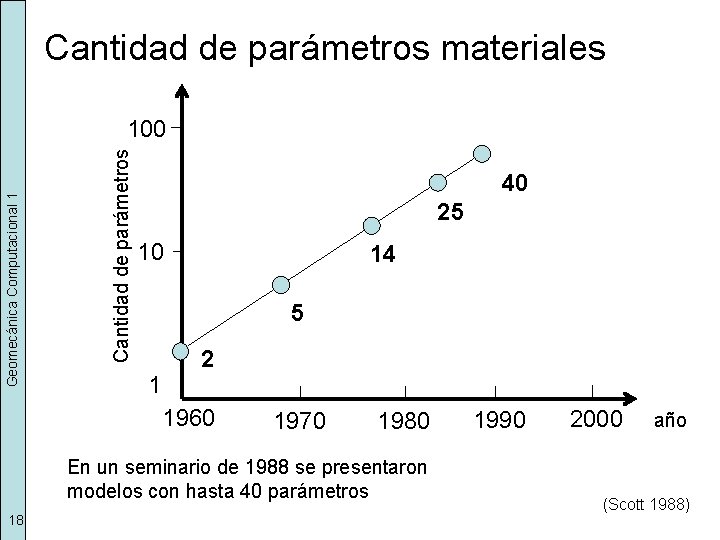
Cantidad de parámetros materiales Cantidad de parámetros Geomecánica Computacional 1 100 40 25 10 14 5 1 2 1960 1970 1980 En un seminario de 1988 se presentaron modelos con hasta 40 parámetros 18 1990 2000 año (Scott 1988)

Geomecánica Computacional 1 Criterios de rotura 19 Los criterios de rotura son funciones del tensor de tensiones que definen cuando ocurre la falla

Geomecánica Computacional 1 Criterios de rotura 20 Tresca y Von Mises Mohr-Coulomb (Wikipedia) (Plaxis UM)

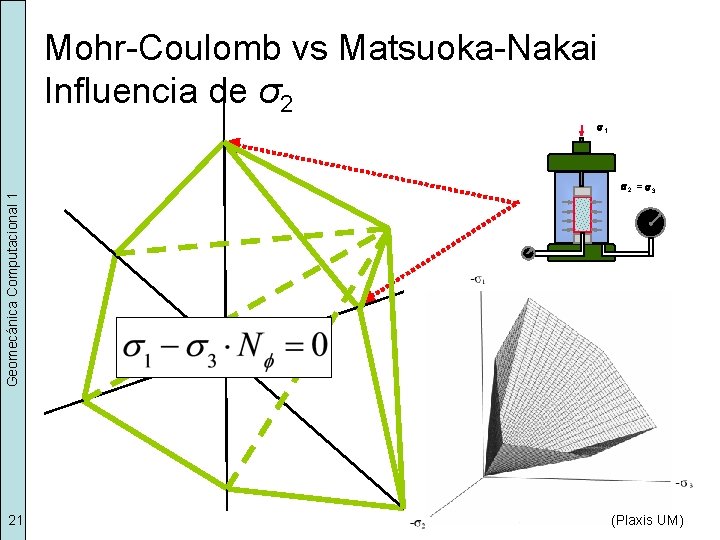
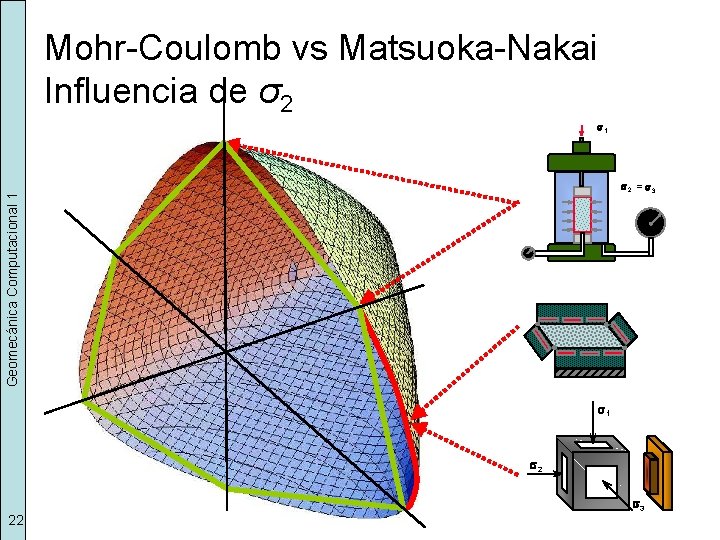
Mohr-Coulomb vs Matsuoka-Nakai Influencia de σ2 Geomecánica Computacional 1 s 1 21 s 2 = s 3 (Plaxis UM)

Mohr-Coulomb vs Matsuoka-Nakai Influencia de σ2 s 1 Geomecánica Computacional 1 s 2 = s 3 s 1 s 2 s 3 22

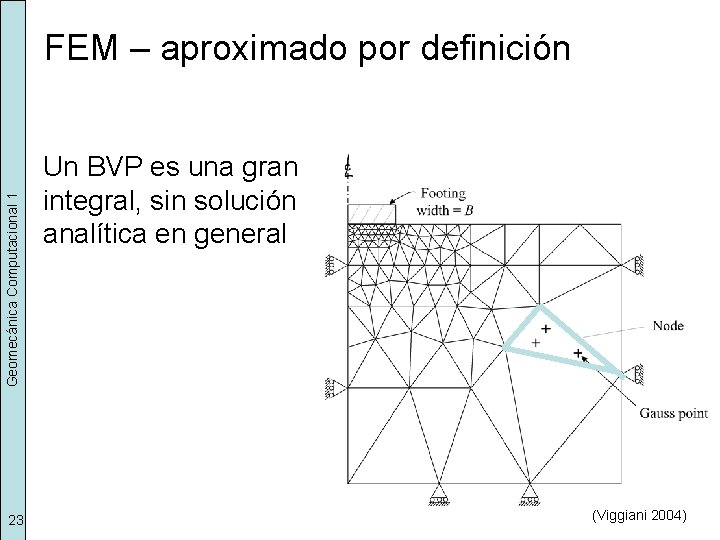
Geomecánica Computacional 1 FEM – aproximado por definición 23 Un BVP es una gran integral, sin solución analítica en general (Viggiani 2004)

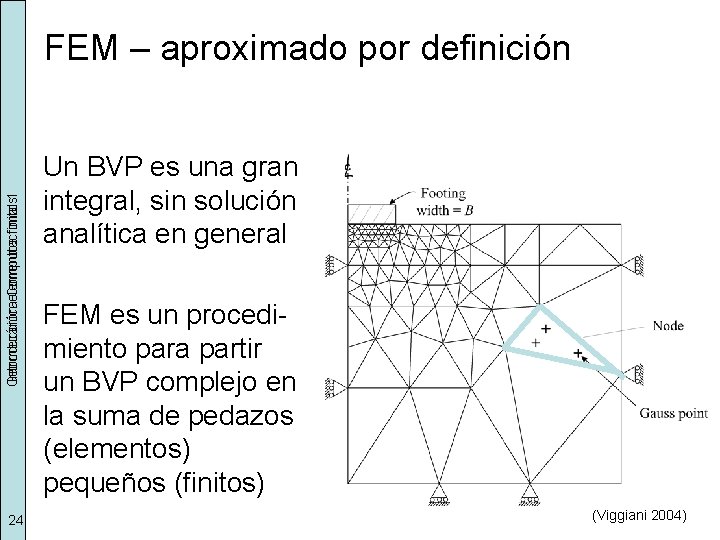
Geomecánica Introducción elementos Computacional finitos 1 FEM – aproximado por definición 24 Un BVP es una gran integral, sin solución analítica en general FEM es un procedimiento para partir un BVP complejo en la suma de pedazos (elementos) pequeños (finitos) (Viggiani 2004)

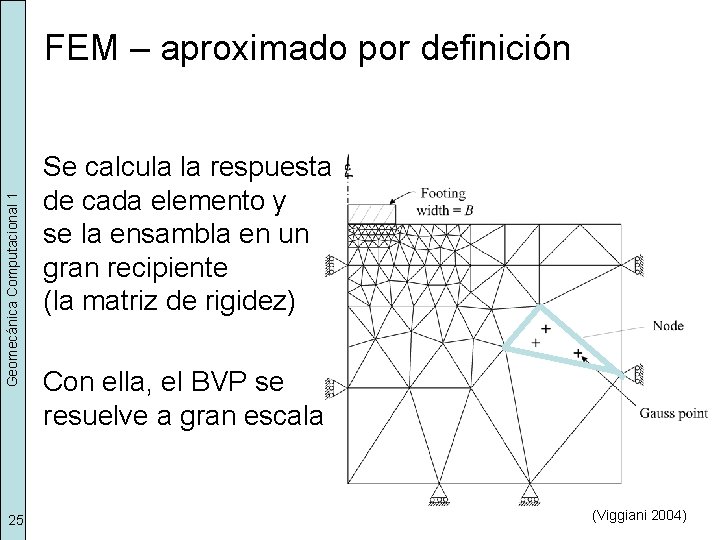
Geomecánica Computacional 1 FEM – aproximado por definición 25 Se calcula la respuesta de cada elemento y se la ensambla en un gran recipiente (la matriz de rigidez) Con ella, el BVP se resuelve a gran escala (Viggiani 2004)

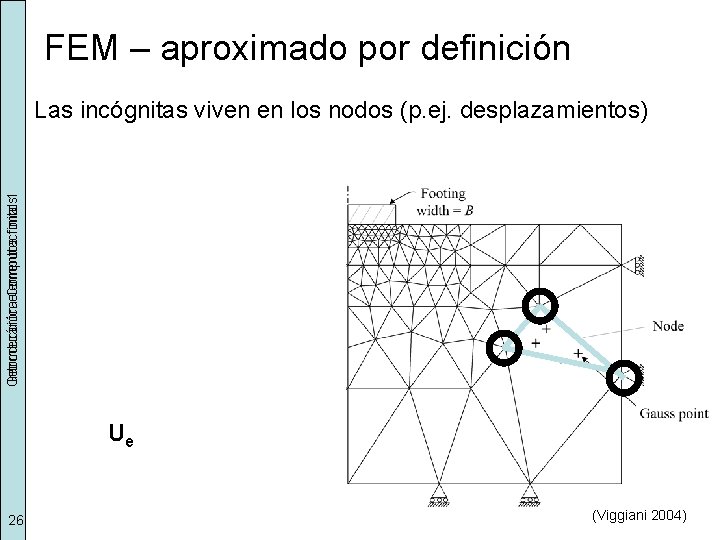
FEM – aproximado por definición Geomecánica Introducción elementos Computacional finitos 1 Las incógnitas viven en los nodos (p. ej. desplazamientos) ue = f(Ue 26 (Viggiani 2004)

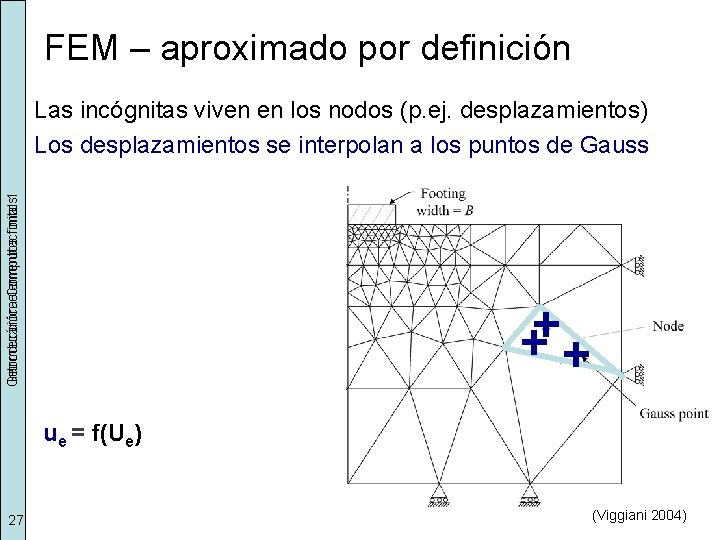
FEM – aproximado por definición Geomecánica Introducción elementos Computacional finitos 1 Las incógnitas viven en los nodos (p. ej. desplazamientos) Los desplazamientos se interpolan a los puntos de Gauss ue = f(Ue) 27 (Viggiani 2004)

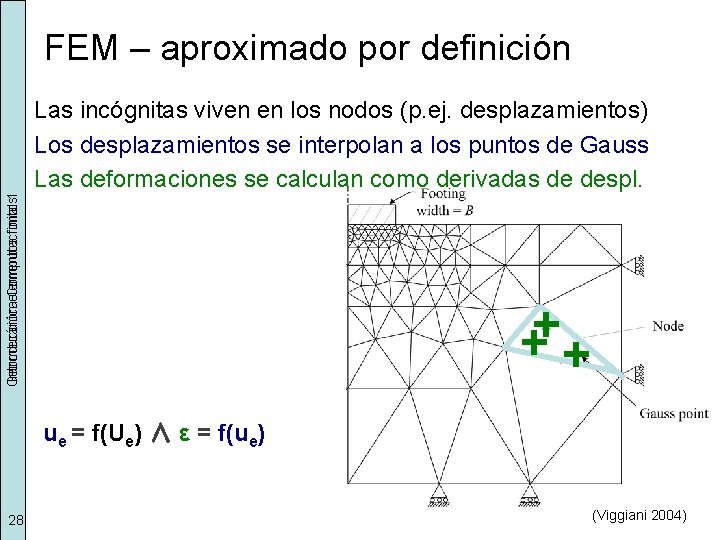
Geomecánica Introducción elementos Computacional finitos 1 FEM – aproximado por definición Las incógnitas viven en los nodos (p. ej. desplazamientos) Los desplazamientos se interpolan a los puntos de Gauss Las deformaciones se calculan como derivadas de despl. ue = f(Ue) ∧ ε = f(ue) 28 (Viggiani 2004)

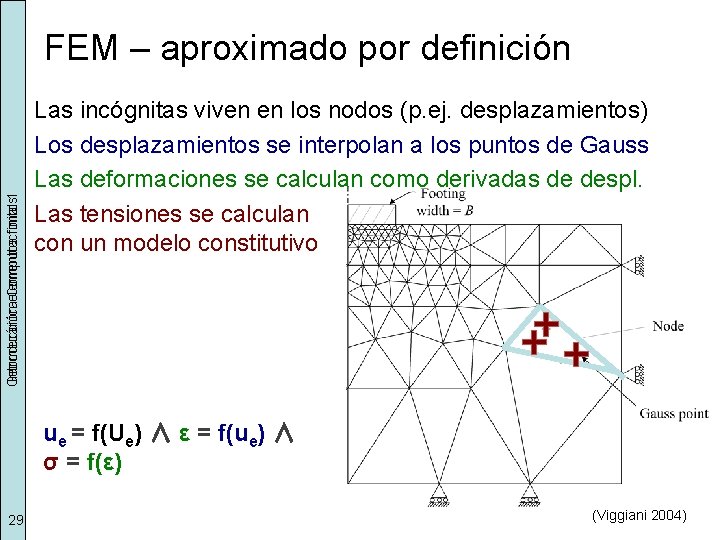
Geomecánica Introducción elementos Computacional finitos 1 FEM – aproximado por definición Las incógnitas viven en los nodos (p. ej. desplazamientos) Los desplazamientos se interpolan a los puntos de Gauss Las deformaciones se calculan como derivadas de despl. Las tensiones se calculan con un modelo constitutivo ue = f(Ue) ∧ ε = f(ue) ∧ σ = f(ε) 29 (Viggiani 2004)

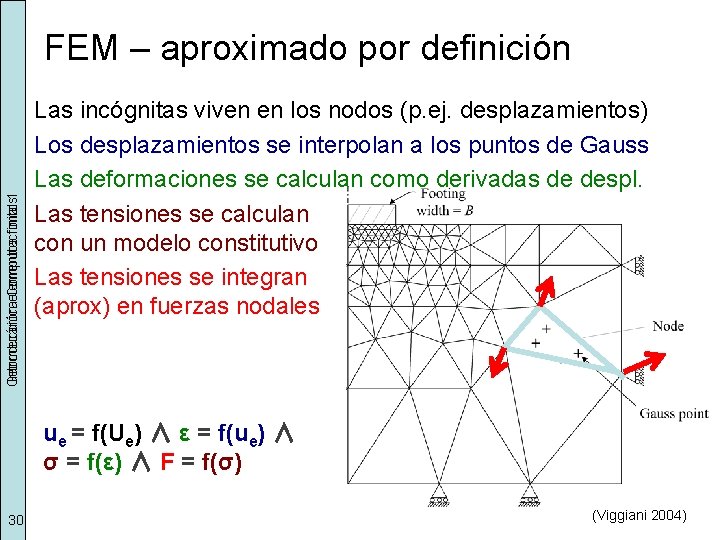
Geomecánica Introducción elementos Computacional finitos 1 FEM – aproximado por definición Las incógnitas viven en los nodos (p. ej. desplazamientos) Los desplazamientos se interpolan a los puntos de Gauss Las deformaciones se calculan como derivadas de despl. Las tensiones se calculan con un modelo constitutivo Las tensiones se integran (aprox) en fuerzas nodales ue = f(Ue) ∧ ε = f(ue) ∧ σ = f(ε) ∧ F = f(σ) 30 (Viggiani 2004)

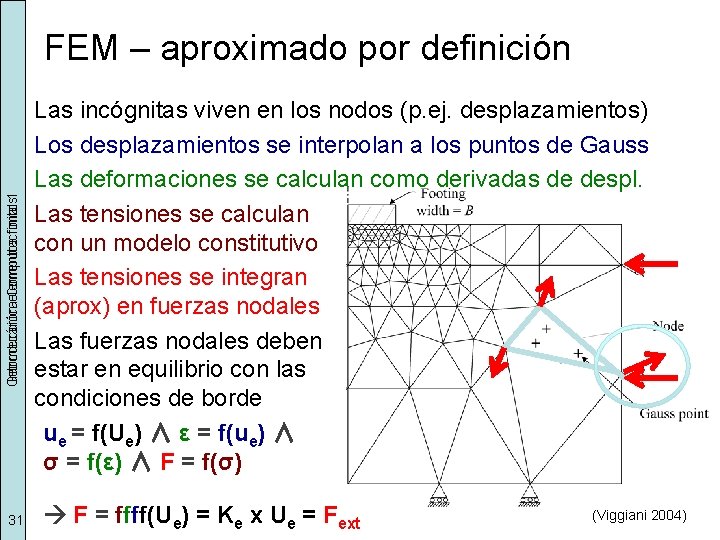
Geomecánica Introducción elementos Computacional finitos 1 FEM – aproximado por definición 31 Las incógnitas viven en los nodos (p. ej. desplazamientos) Los desplazamientos se interpolan a los puntos de Gauss Las deformaciones se calculan como derivadas de despl. Las tensiones se calculan con un modelo constitutivo Las tensiones se integran (aprox) en fuerzas nodales Las fuerzas nodales deben estar en equilibrio con las condiciones de borde ue = f(Ue) ∧ ε = f(ue) ∧ σ = f(ε) ∧ F = f(σ) F = ffff(Ue) = Ke x Ue = Fext (Viggiani 2004)

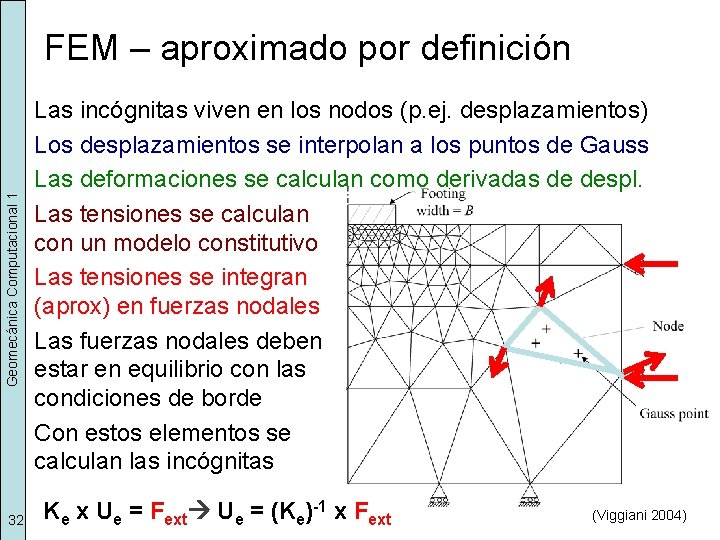
Geomecánica Computacional 1 FEM – aproximado por definición 32 Las incógnitas viven en los nodos (p. ej. desplazamientos) Los desplazamientos se interpolan a los puntos de Gauss Las deformaciones se calculan como derivadas de despl. Las tensiones se calculan con un modelo constitutivo Las tensiones se integran (aprox) en fuerzas nodales Las fuerzas nodales deben estar en equilibrio con las condiciones de borde Con estos elementos se calculan las incógnitas Ke x Ue = Fext Ue = (Ke)-1 x Fext (Viggiani 2004)

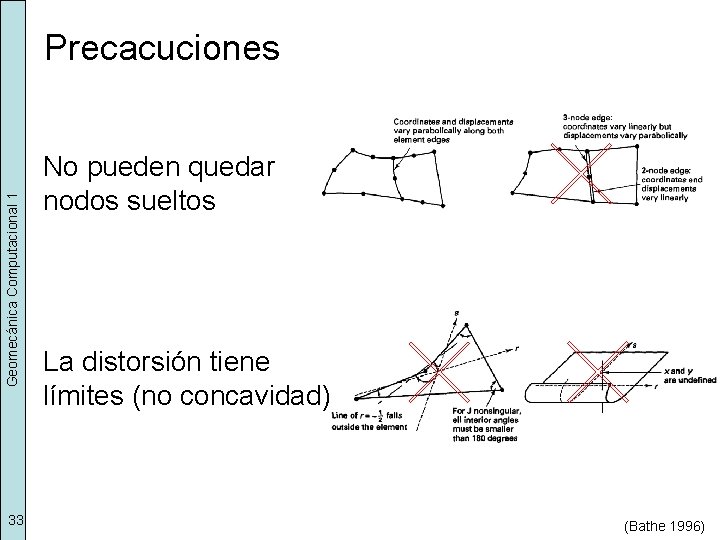
Geomecánica Computacional 1 Precacuciones 33 No pueden quedar nodos sueltos La distorsión tiene límites (no concavidad) (Bathe 1996)

Geomecánica Computacional 1 Criterios de mallado 34 La malla es la discretización de un problema continuo La densidad local de la malla depende del gradiente de la solución (de cómo “cambian los colores”) La malla es una combinación de • Tipo de elemento (en Plaxis, T 6 y T 15) • Tamaño medio de elementos • Refinamientos locales

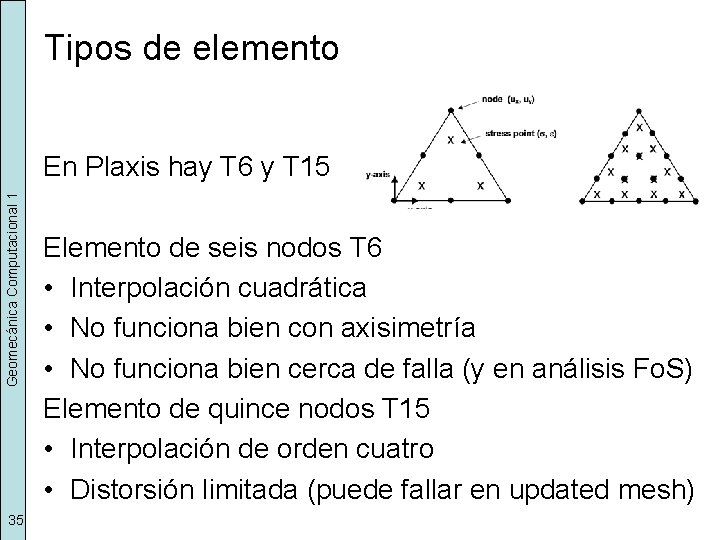
Tipos de elemento Geomecánica Computacional 1 En Plaxis hay T 6 y T 15 35 Elemento de seis nodos T 6 • Interpolación cuadrática • No funciona bien con axisimetría • No funciona bien cerca de falla (y en análisis Fo. S) Elemento de quince nodos T 15 • Interpolación de orden cuatro • Distorsión limitada (puede fallar en updated mesh)

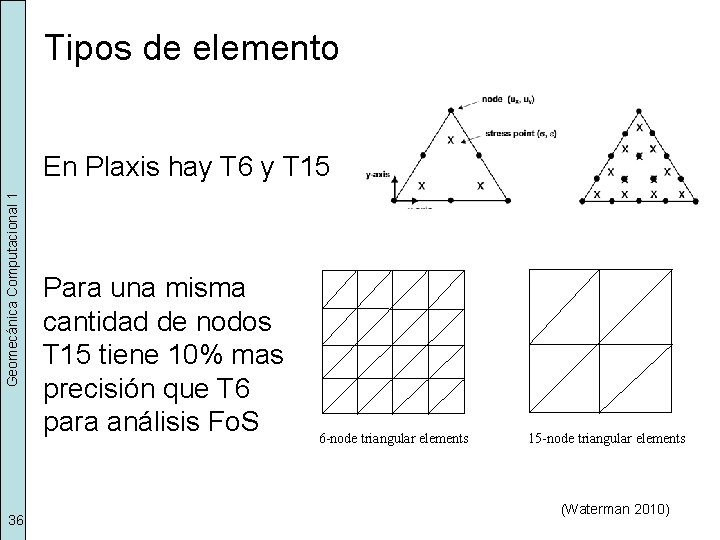
Tipos de elemento Geomecánica Computacional 1 En Plaxis hay T 6 y T 15 36 Para una misma cantidad de nodos T 15 tiene 10% mas precisión que T 6 para análisis Fo. S 6 -node triangular elements 15 -node triangular elements (Waterman 2010)

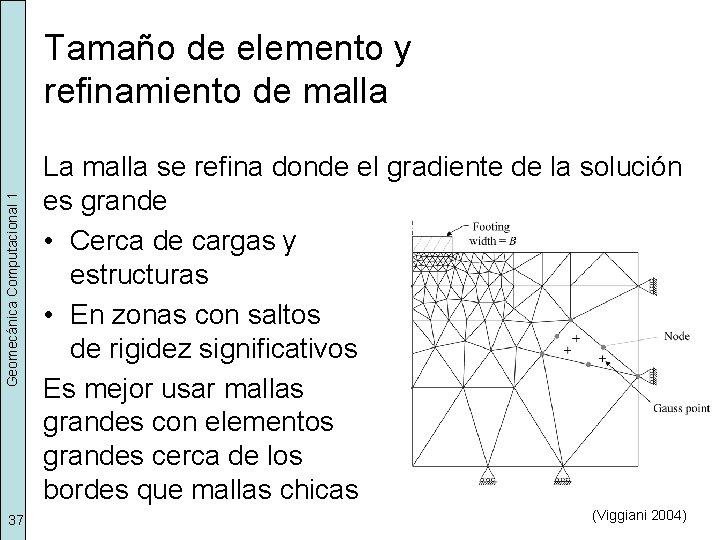
Geomecánica Computacional 1 Tamaño de elemento y refinamiento de malla 37 La malla se refina donde el gradiente de la solución es grande • Cerca de cargas y estructuras • En zonas con saltos de rigidez significativos Es mejor usar mallas grandes con elementos grandes cerca de los bordes que mallas chicas (Viggiani 2004)

Geomecánica Computacional 1 Tamaño de elemento y refinamiento de malla 38 En Plaxis, el tamaño de los elementos se calcula con la expresión Donde nc es un número que se define con la tabla very coarse - medium - fine - very fine o se entra a mano (opción experta)

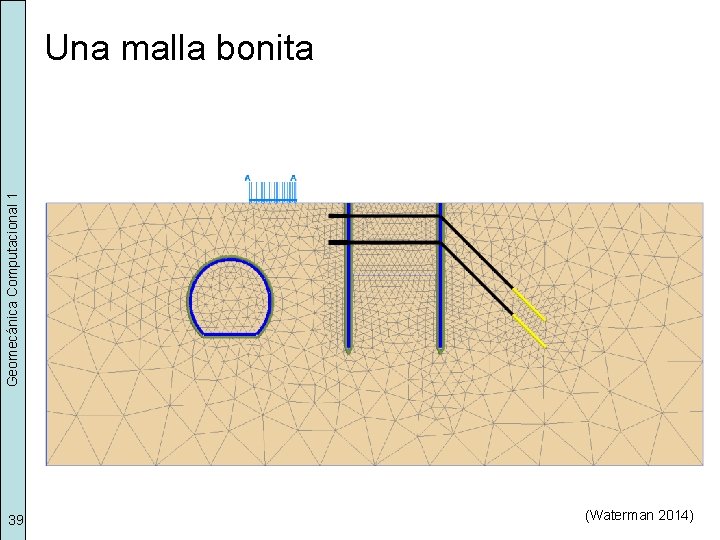
Geomecánica Computacional 1 Una malla bonita 39 (Waterman 2014)

Geomecánica Computacional 1 Condiciones iniciales y de borde 40 Condiciones de borde: restricciones permanentes • Dirichlet: determinan el valor de la incógnita en el contorno de la malla (p. ej. desplazamientos) • Von Neumann: determinan el valor de derivadas de la incógnita (p. ej. fuerzas)

Geomecánica Computacional 1 Condiciones iniciales y de borde 41 Condiciones de borde: restricciones permanentes • Dirichlet: determinan el valor de la incógnita en el contorno de la malla (p. ej. desplazamientos) • Von Neumann: determinan el valor de derivadas de la incógnita (p. ej. fuerzas) Condiciones iniciales (en todos los nodos / GP) • Desplazamientos • Fuerzas • Variables de estado (tensión, def. plástica, etc. )

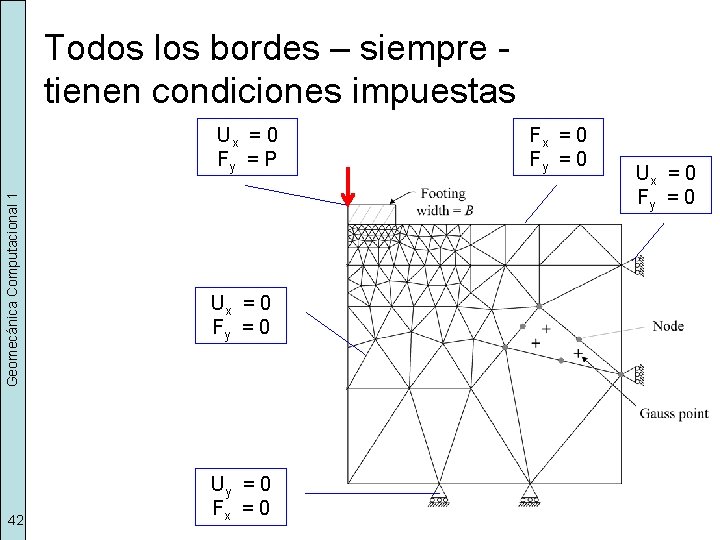
Todos los bordes – siempre tienen condiciones impuestas Geomecánica Computacional 1 Ux = 0 Fy = P 42 Ux = 0 Fy = 0 Uy = 0 Fx = 0 Fy = 0 Ux = 0 Fy = 0

Geomecánica Computacional 1 Tensiones iniciales 43 Representan el estado (de equilibrio) inicial del terreno • Peso propio • Historia de tensiones (p. ej. K 0)

Geomecánica Computacional 1 Tensiones iniciales 44 Representan el estado (de equilibrio) inicial del terreno • Peso propio • Historia de tensiones (p. ej. K 0) Se pueden calcular reproduciendo la historia de tensiones (laborioso y poco práctico)

Geomecánica Computacional 1 Tensiones iniciales 45 Representan el estado (de equilibrio) inicial del terreno • Peso propio • Historia de tensiones (p. ej. K 0) Se pueden calcular reproduciendo la historia de tensiones (laborioso y poco práctico) Para casos simples se pueden imponer y luego verificar equilibrio y admisibilidad plástica

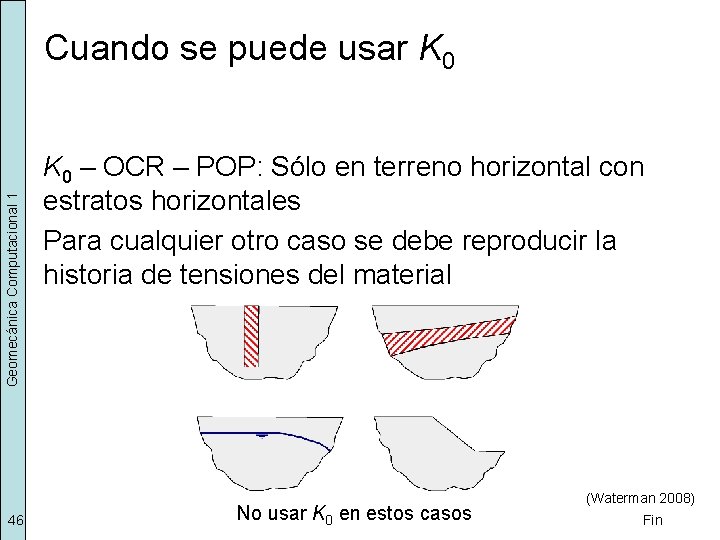
Geomecánica Computacional 1 Cuando se puede usar K 0 46 K 0 – OCR – POP: Sólo en terreno horizontal con estratos horizontales Para cualquier otro caso se debe reproducir la historia de tensiones del material No usar K 0 en estos casos (Waterman 2008) Fin

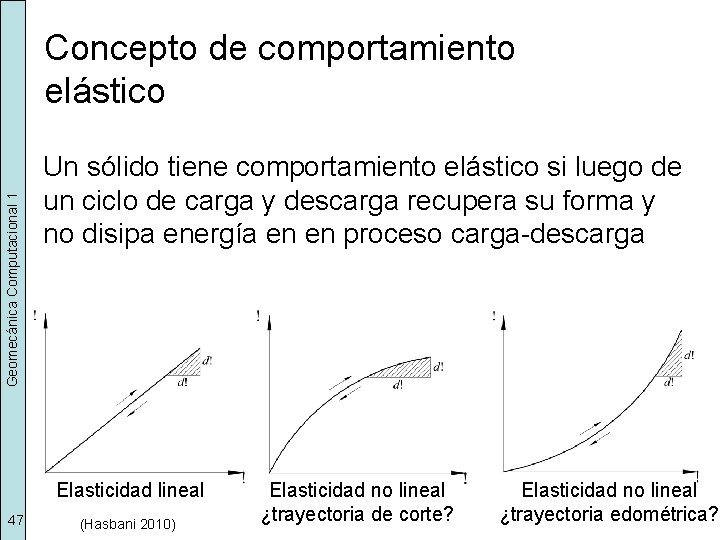
Geomecánica Computacional 1 Concepto de comportamiento elástico Un sólido tiene comportamiento elástico si luego de un ciclo de carga y descarga recupera su forma y no disipa energía en en proceso carga-descarga Elasticidad lineal 47 (Hasbani 2010) Elasticidad no lineal ¿trayectoria de corte? Elasticidad no lineal ¿trayectoria edométrica?

Elasticidad lineal isotrópica Geomecánica Computacional 1 La elasticidad lineal isotrópica se escribe como 48 Tiene dos parámetros materiales: E, ν Para deformación plana tiene la forma matricial

Geomecánica Computacional 1 G 0: Teoría de contacto elástico 49 La rigidez elástica es proporcional a la presión y densidad • Contacto esférico • Contacto cono-placa

Geomecánica Computacional 1 Correlaciones para G 0 50 (Pestana 2010)

El concepto de las “propiedades dinámicas” de los suelos Geomecánica Computacional 1 El movimiento de un punto material obedece a 51 Esto prueba que la única “propiedad dinámica del suelo” es su masa En ingeniería civil se resuelve el problema Y se define una “rigidez dinámica”

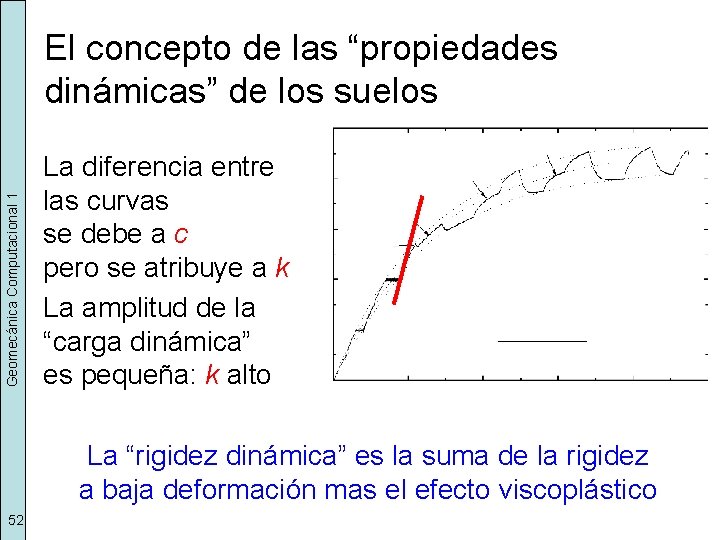
Geomecánica Computacional 1 El concepto de las “propiedades dinámicas” de los suelos La diferencia entre las curvas se debe a c pero se atribuye a k La amplitud de la “carga dinámica” es pequeña: k alto La “rigidez dinámica” es la suma de la rigidez a baja deformación mas el efecto viscoplástico 52

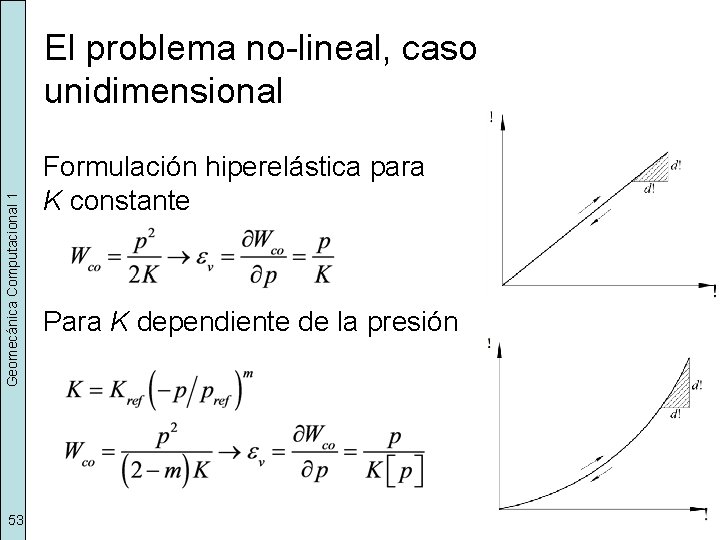
Geomecánica Computacional 1 El problema no-lineal, caso unidimensional 53 Formulación hiperelástica para K constante Para K dependiente de la presión

El problema no-lineal, caso unidimensional Geomecánica Computacional 1 Explícito: parece hiperelasticidad, es hipoelasticidad 54 Implícito: es hiperelasticidad, puede despejarse pn+1

El problema no-lineal, caso unidimensional Geomecánica Computacional 1 Datos Solución implícita Solución explícita 55 Cant pasos 1 10 1000 Presión -156 k. Pa -171 k. Pa -173 k. Pa -73 k. Pa

Geomecánica Computacional 1 Esquema de Newton-Raphson 56 Se parte de un estado convergido Se impone el incremento de def. El problema a resolver es Que se reescribe implícita (se caen los (n+1)) Este problema se resuelve a partir de pn y se itera en p hasta que se alcanza la condición F = 0

Geomecánica Computacional 1 Esquema de Newton-Raphson 57 Para eso se hace una expansión de Taylor de F y se despeja el incremento de tensión Δp que permite calcular La derivada es (Cuando anda) el esquema es robusto y de convergencia rápida

Geomecánica Computacional 1 Cómo funciona 58

Geomecánica Computacional 1 Cómo funciona 59

Geomecánica Computacional 1 Cómo funciona 60

Geomecánica Computacional 1 Cómo funciona 61

Geomecánica Computacional 1 Cómo funciona 62

Geomecánica Computacional 1 Cómo funciona 63

Geomecánica Computacional 1 Cómo se arregla 64 El reducido radio de convergencia de N-R originó cientos de métodos de integración Una manera sencilla de resolver el problema para el ejemplo es complementar a N-R con bisección

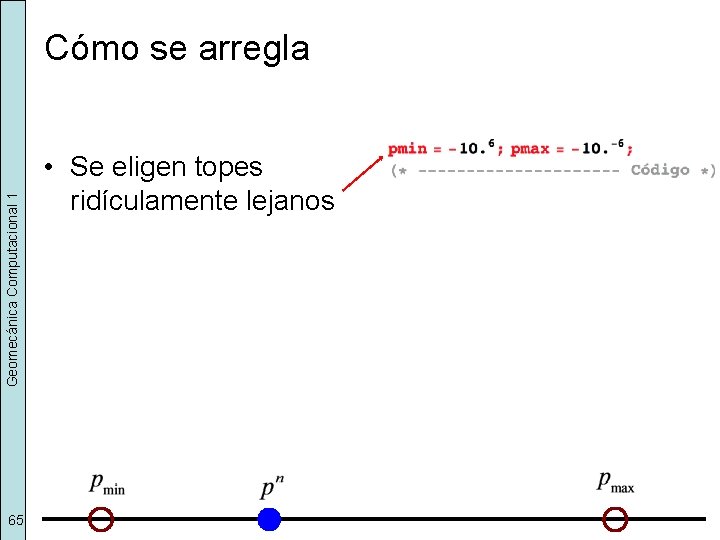
Geomecánica Computacional 1 Cómo se arregla 65 • Se eligen topes ridículamente lejanos

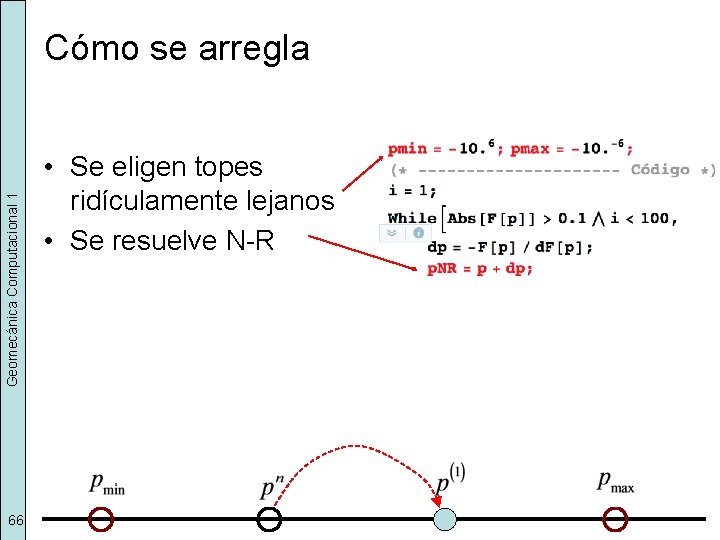
Geomecánica Computacional 1 Cómo se arregla 66 • Se eligen topes ridículamente lejanos • Se resuelve N-R

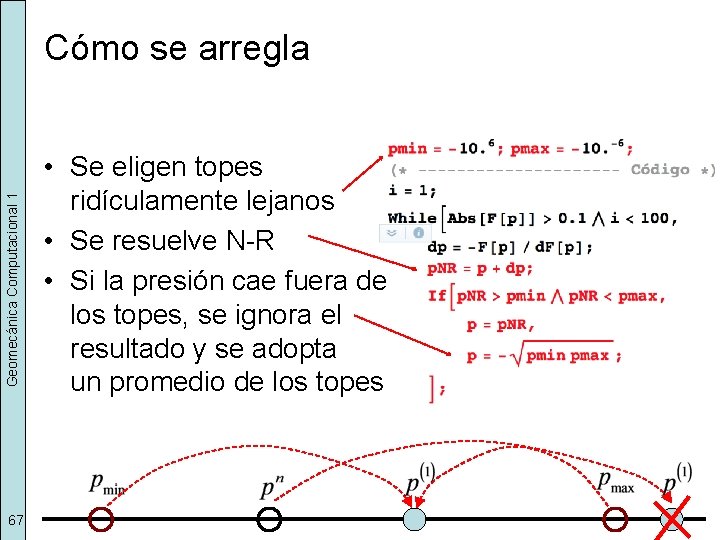
Geomecánica Computacional 1 Cómo se arregla 67 • Se eligen topes ridículamente lejanos • Se resuelve N-R • Si la presión cae fuera de los topes, se ignora el resultado y se adopta un promedio de los topes

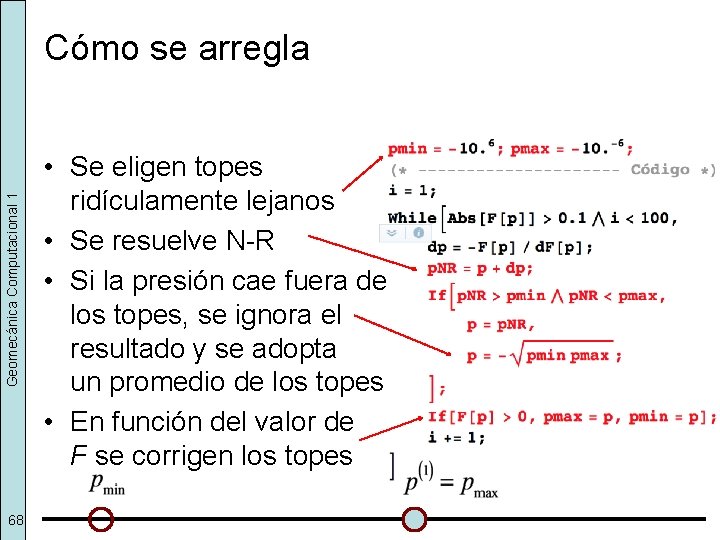
Geomecánica Computacional 1 Cómo se arregla 68 • Se eligen topes ridículamente lejanos • Se resuelve N-R • Si la presión cae fuera de los topes, se ignora el resultado y se adopta un promedio de los topes • En función del valor de F se corrigen los topes

Geomecánica Computacional 1 Bibliografía esencial (en orden decreciente) 69 • Potts et al. Guideline for the use of advanced numerical analysis. COST Action C 7. Thomas Telford 2002. • Potts & Zdravkovic. Finite element analysis in geotechnical engineering. Thomas Telford 1999. • Chen & Mizuno. Nonlinear analysis in soil mechanics. Elsevier 1990. • Muir Wood. Geotechnical modelling. 2004. • USACE. Geotechnical analysis by the FEM. Report ETL 1110 -2 -544. • Puzrin. Constitutive modelling in geomechanics. Springer 2012. • Yu. Plasticity and geotechnics. Springer 2006. • Bull. Numerical analysis modelling geomechanics. Spon Press 2003.

Geomecánica Computacional 1 Bibliografía esencial (en orden decreciente) 70 • Bull. Numerical analysis modelling geomechanics. Spon Press 2003. • Zienkiewicz et al. Computational geomechanics. Wiley 1999. • Lewis&Schrefler. The FEM in the static and dynamic deformation and consolidation of porous media. Wiley 1998. • Bathe, K. Finite element procedures. Bathe. • Zienkiewicz et al. The finite element method. Butterworth-Heinemann. • Olivella & Agelet. Mecánica de medios continuos para ingenieros. UPC.
 Geotecnia 2 ing unlp
Geotecnia 2 ing unlp Mdulo
Mdulo Aritmética computacional
Aritmética computacional Complexidade computacional
Complexidade computacional Complexidade computacional
Complexidade computacional Sistema computacional
Sistema computacional Psiquiatria computacional
Psiquiatria computacional Ufrj
Ufrj Auditoria computacional
Auditoria computacional Complexidade computacional
Complexidade computacional Exactas unlp
Exactas unlp Patolgie
Patolgie Curso de ingreso psicología unlp
Curso de ingreso psicología unlp Geotecnia
Geotecnia Geotecnia
Geotecnia I
I Geotecnia
Geotecnia Geotecnia
Geotecnia Circulo de mohr
Circulo de mohr Geotecnia
Geotecnia Geotecnia
Geotecnia Geotecnia
Geotecnia Hamlet act iii scene iii
Hamlet act iii scene iii Pwc
Pwc Investigador
Investigador Discoria
Discoria Nsds iii
Nsds iii Which event from acts ii and iii
Which event from acts ii and iii Bazel iii
Bazel iii Wppsi subtest
Wppsi subtest Mrp iii
Mrp iii John d. rockefeller iii
John d. rockefeller iii Napoleon iii rule
Napoleon iii rule Alfred mansour iii md
Alfred mansour iii md Hamlet act iii scene i
Hamlet act iii scene i Pentaaqua thiocyanato iron(iii)
Pentaaqua thiocyanato iron(iii) Apollo with battling lapiths and centaurs
Apollo with battling lapiths and centaurs George nichols iii
George nichols iii Nickel iii carbonate
Nickel iii carbonate Referens iii
Referens iii Error control tcp
Error control tcp Objaw kustnera
Objaw kustnera National association of hbcu title iii administrators
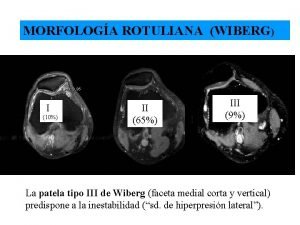
National association of hbcu title iii administrators Displasia tipo ii de wiberg
Displasia tipo ii de wiberg Basel pillars
Basel pillars Type iii binary compounds examples
Type iii binary compounds examples Pentium iii
Pentium iii Nelson denny test
Nelson denny test Cantos tercer domingo de cuaresma ciclo c
Cantos tercer domingo de cuaresma ciclo c Smartlegal polygon
Smartlegal polygon Iii kryterium ewaluacji
Iii kryterium ewaluacji Acesso central femoral
Acesso central femoral Basel iii liquidity coverage ratio
Basel iii liquidity coverage ratio Displasia
Displasia Title iii requirements
Title iii requirements Climax of hamlet
Climax of hamlet Iii zasada dynamiki
Iii zasada dynamiki Icaap nedir
Icaap nedir Falsari divina commedia
Falsari divina commedia Erf.
Erf. Gilbert newton iii
Gilbert newton iii English level iii
English level iii Dziady cz 3 motywy biblijne
Dziady cz 3 motywy biblijne Mrp przykład
Mrp przykład Certificate iii in pathology collections
Certificate iii in pathology collections Evolution of class iii treatment in orthodontics
Evolution of class iii treatment in orthodontics Exercícios present perfect 9 ano com gabarito doc
Exercícios present perfect 9 ano com gabarito doc Natura morta con maschere iii
Natura morta con maschere iii Kara walker: darkytown rebellion, 2001 stadia ii
Kara walker: darkytown rebellion, 2001 stadia ii Hcps iii
Hcps iii Slide sejarah tingkatan 2 bab 7
Slide sejarah tingkatan 2 bab 7