Function Approximation w Function approximation Chapters 13 14

Function Approximation w Function approximation (Chapters 13 & 14) -- method of least squares -- minimize the residuals -- given data of points have noises -- the purpose is to find the trend represented by data. w Function interpolation (Chapters 15 & 16) -- approximating function match the given data exactly -- given data of points are precise -- the purpose is to find data between these points

Interpolation and Regression

Chapter 13 Curve Fitting: Fitting a Straight Line

Least Square Regression Curve Fitting w Statistics Review w Linear Least Square Regression w Linearization of Nonlinear Relationships w MATLAB Functions w

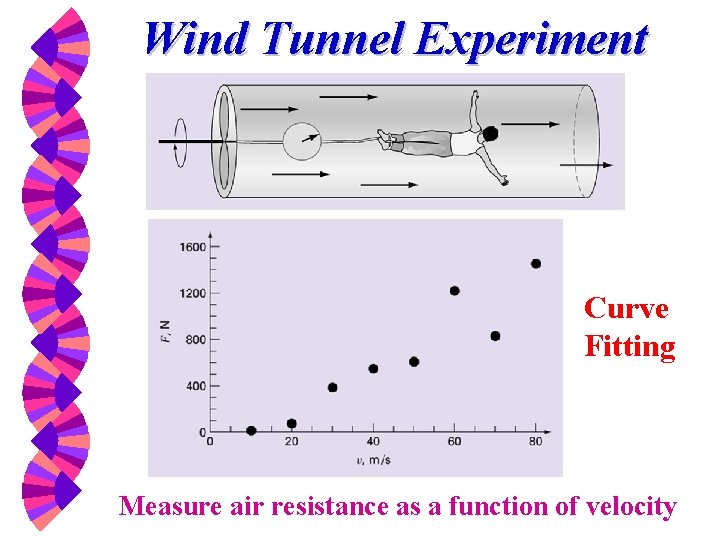
Wind Tunnel Experiment Curve Fitting Measure air resistance as a function of velocity

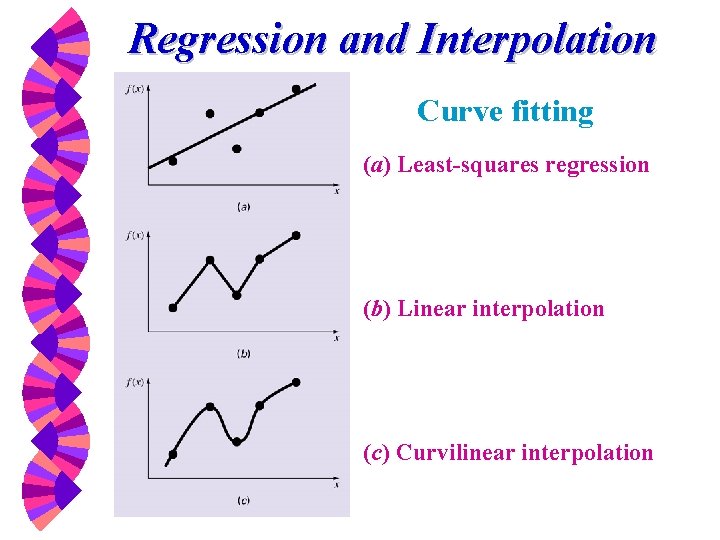
Regression and Interpolation Curve fitting (a) Least-squares regression (b) Linear interpolation (c) Curvilinear interpolation

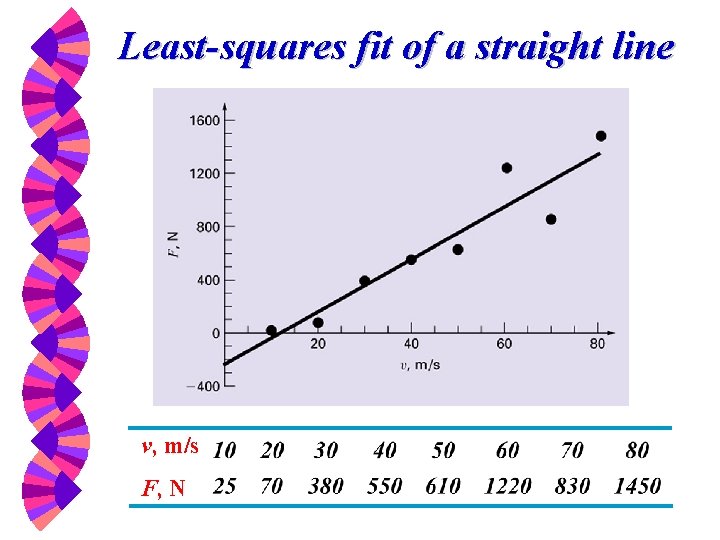
Least-squares fit of a straight line v, m/s F, N

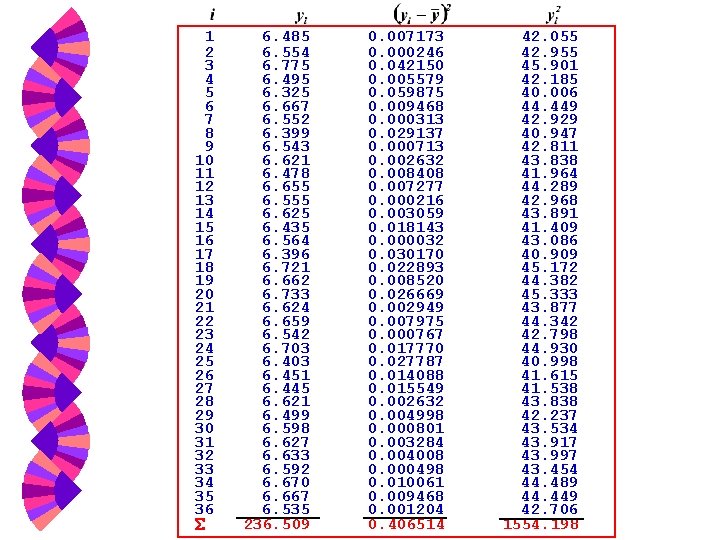
Simple Statistics Measurement of the coefficient of thermal expansion of structural steel [ 10 6 in/(in F)] Mean, standard deviation, variance, etc.

Statistics Review w Arithmetic mean w Standard deviation about the mean w Variance (spread) w Coefficient of variation (c. v. )

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 6. 485 6. 554 6. 775 6. 495 6. 325 6. 667 6. 552 6. 399 6. 543 6. 621 6. 478 6. 655 6. 555 6. 625 6. 435 6. 564 6. 396 6. 721 6. 662 6. 733 6. 624 6. 659 6. 542 6. 703 6. 451 6. 445 6. 621 6. 499 6. 598 6. 627 6. 633 6. 592 6. 670 6. 667 6. 535 236. 509 0. 007173 0. 000246 0. 042150 0. 005579 0. 059875 0. 009468 0. 000313 0. 029137 0. 000713 0. 002632 0. 008408 0. 007277 0. 000216 0. 003059 0. 018143 0. 000032 0. 030170 0. 022893 0. 008520 0. 026669 0. 002949 0. 007975 0. 000767 0. 017770 0. 027787 0. 014088 0. 015549 0. 002632 0. 004998 0. 000801 0. 003284 0. 004008 0. 000498 0. 010061 0. 009468 0. 001204 0. 406514 42. 055 42. 955 45. 901 42. 185 40. 006 44. 449 42. 929 40. 947 42. 811 43. 838 41. 964 44. 289 42. 968 43. 891 41. 409 43. 086 40. 909 45. 172 44. 382 45. 333 43. 877 44. 342 42. 798 44. 930 40. 998 41. 615 41. 538 43. 838 42. 237 43. 534 43. 917 43. 997 43. 454 44. 489 44. 449 42. 706 1554. 198

Coefficient of Thermal Expansion Mean Sum of the square of residuals Standard deviation Variance Coefficient of variation

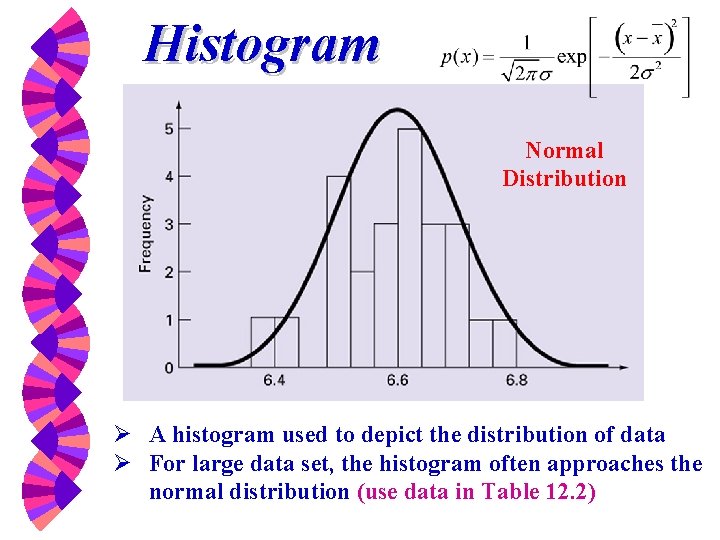
Histogram Normal Distribution Ø A histogram used to depict the distribution of data Ø For large data set, the histogram often approaches the normal distribution (use data in Table 12. 2)

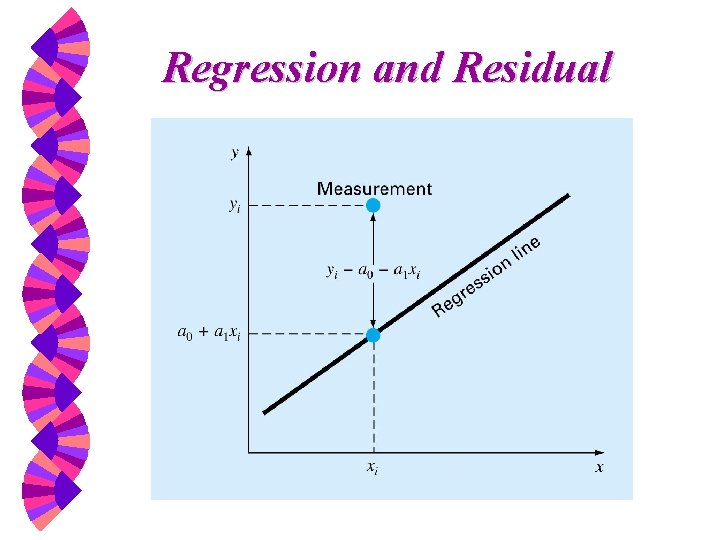
Regression and Residual

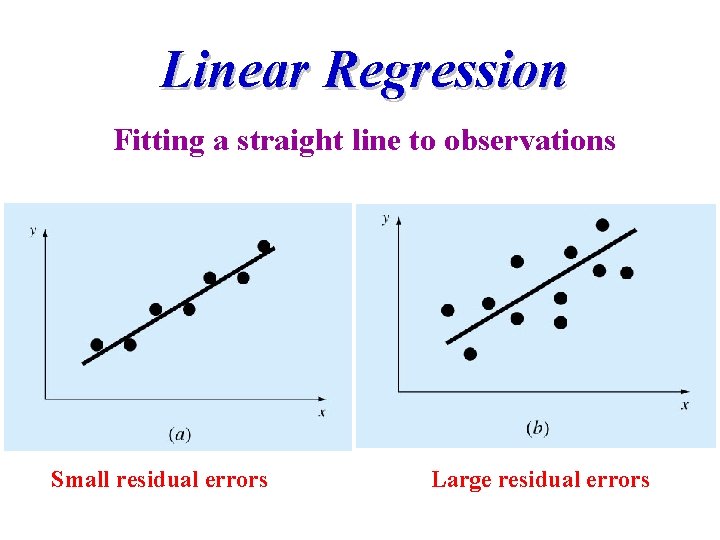
Linear Regression Fitting a straight line to observations Small residual errors Large residual errors

Linear Regression w Equation for straight line w Difference between observation and line w ei is the residual or error

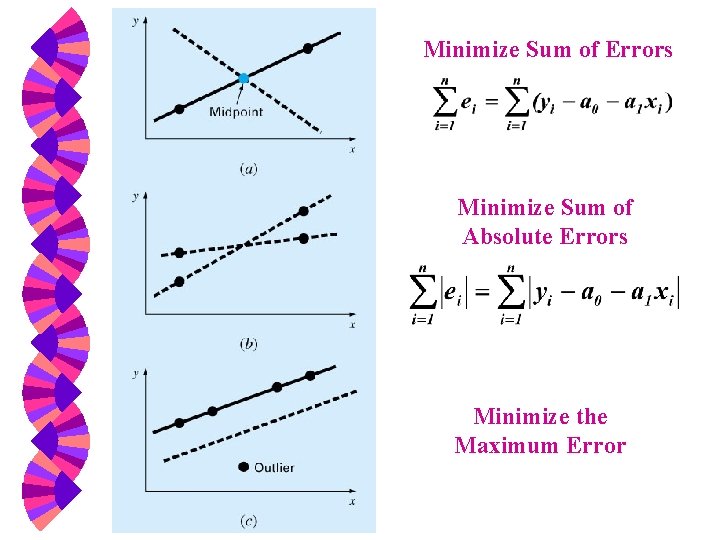
Least Squares Approximation w Minimizing Residuals (Errors) minimum average error (cancellation) w minimum absolute error w minimax error (minimizing the maximum error) w least squares (linear, quadratic, …. ) w

Minimize Sum of Errors Minimize Sum of Absolute Errors Minimize the Maximum Error

Linear Least Squares Minimize total square-error w Straight line approximation w w Not likely to pass all points if n > 2

Linear Least Squares w Total square-error function: sum of the squares of the residuals w Minimizing square-error Sr(a 0 , a 1) Solve for (a 0 , a 1)

Linear Least Squares w Minimize w Normal equation y = a 0 + a 1 x

Advantage of Least Squares w Positive differences do not cancel negative differences w Differentiation is straightforward w weighted differences w Small differences become smaller and large differences are magnified

Linear Least Squares w Use sum( ) in MATLAB

Correlation Coefficient w Sum of squares of the residuals with respect to the mean w Sum of squares of the residuals with respect to the regression line w Coefficient of determination w Correlation coefficient

Correlation Coefficient Alternative formulation of correlation coefficient w More convenient for computer implementation w

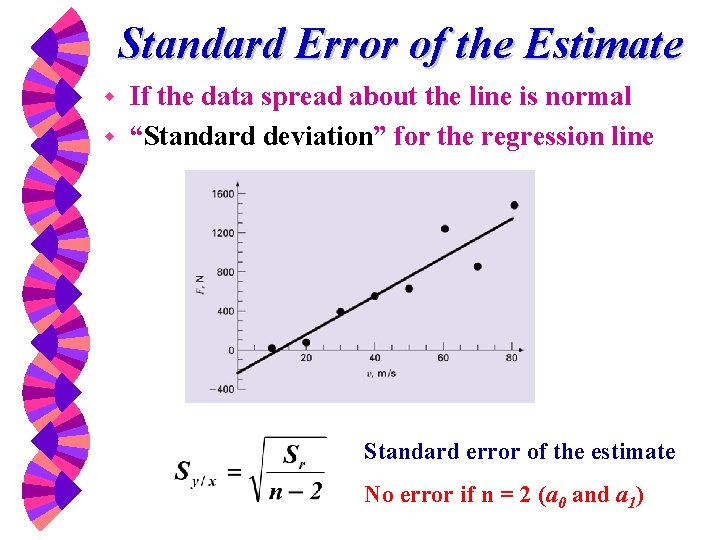
Standard Error of the Estimate If the data spread about the line is normal w “Standard deviation” for the regression line w Standard error of the estimate No error if n = 2 (a 0 and a 1)

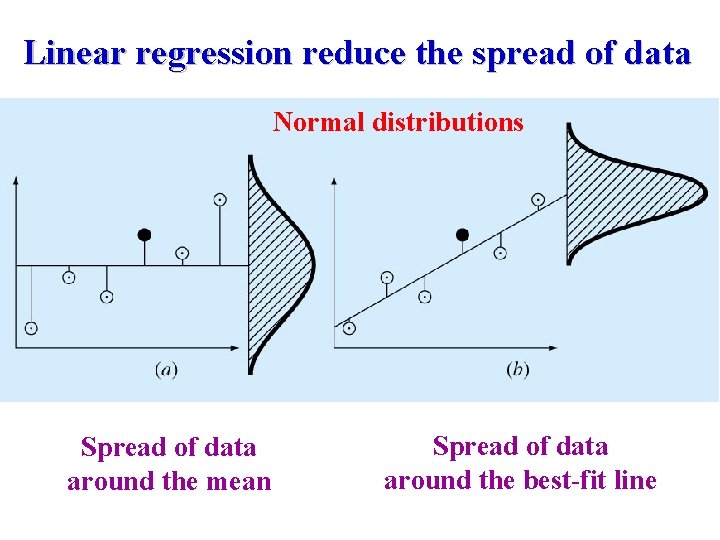
Linear regression reduce the spread of data Normal distributions Spread of data around the mean Spread of data around the best-fit line

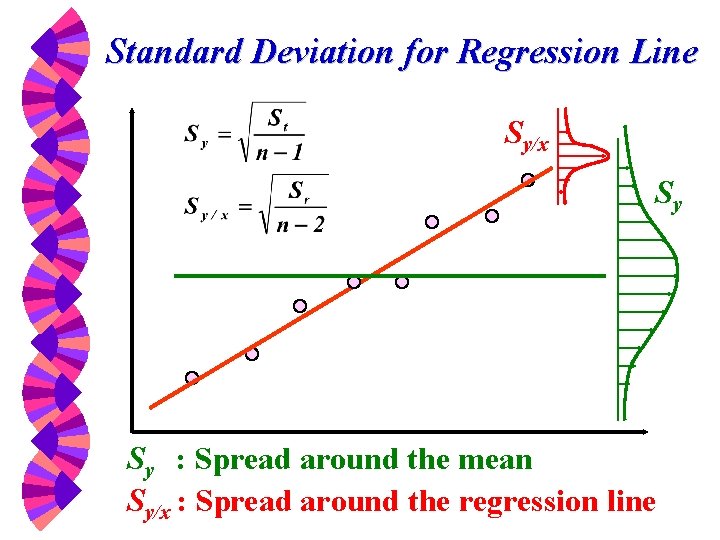
Standard Deviation for Regression Line Sy/x Sy Sy : Spread around the mean Sy/x : Spread around the regression line

Example: Linear Regression

Example: Linear Regression Standard deviation about the mean Standard error of the estimate Correlation coefficient

Linear Least Square Regression

Modified MATLAB M-File

» x=1: 7 x = 1 2 3 4 5 6 7 » y=[0. 5 2. 0 4. 0 3. 5 6. 0 5. 5] y = 0. 5000 2. 0000 4. 0000 3. 5000 6. 0000 » s=linear_LS(x, y) a 0 = 0. 0714 a 1 = 0. 8393 x y (a 0+a 1*x) (y-a 0 -a 1*x) 1. 0000 0. 5000 0. 9107 -0. 4107 2. 0000 2. 5000 1. 7500 0. 7500 3. 0000 2. 5893 -0. 5893 4. 0000 3. 4286 0. 5714 5. 0000 3. 5000 4. 2679 -0. 7679 6. 0000 5. 1071 0. 8929 7. 0000 5. 5000 5. 9464 -0. 4464 err = 2. 9911 Sum of squares of residuals Sr Syx = 0. 7734 Standard error of the estimate r = 0. 9318 Correlation coefficient s = 0. 0714 0. 8393 y =0. 0714 + 0. 8393 x 5. 5000

» x=0: 1: 7; y=[0. 5 2 4 3. 5 6. 0 5. 5]; Linear regression y = 0. 0714+0. 8393 x Error : Sr = 2. 9911 correlation coefficient : r = 0. 9318

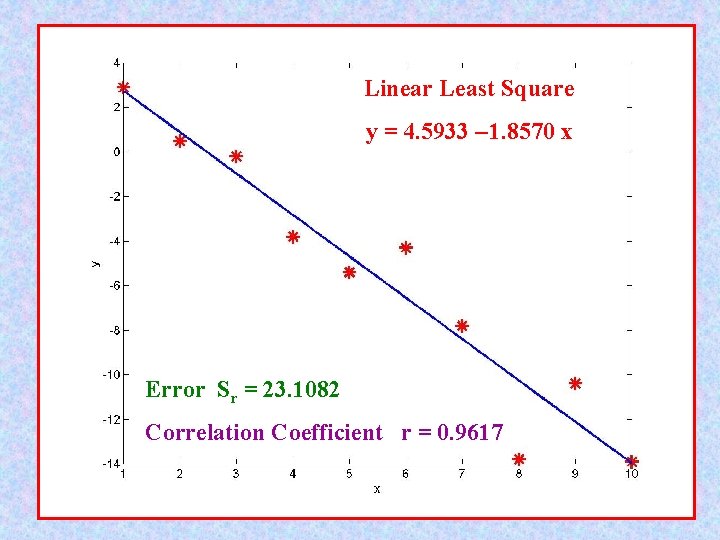
function [x, y] = example 1 x = [ 1 2 3 4 5 6 7 8 9 10]; y = [2. 9 0. 5 -0. 2 -3. 8 -5. 4 -4. 3 -7. 8 -13. 8 -10. 4 -13. 9]; » [x, y]=example 1; » s=Linear_LS(x, y) a 0 = 4. 5933 a 1 = -1. 8570 x y 1. 0000 2. 9000 2. 0000 0. 5000 3. 0000 -0. 2000 4. 0000 -3. 8000 5. 0000 -5. 4000 6. 0000 -4. 3000 7. 0000 -7. 8000 8. 0000 -13. 8000 9. 0000 -10. 4000 10. 0000 -13. 9000 err = 23. 1082 Syx = 1. 6996 r = 0. 9617 s = 4. 5933 -1. 8570 (a 0+a 1*x) (y-a 0 -a 1*x) 2. 7364 0. 1636 0. 8794 -0. 3794 -0. 9776 0. 7776 -2. 8345 -0. 9655 -4. 6915 -0. 7085 -6. 5485 2. 2485 -8. 4055 0. 6055 -10. 2624 -3. 5376 -12. 1194 1. 7194 -13. 9764 0. 0764 r = 0. 9617 y = 4. 5933 1. 8570 x

Linear Least Square y = 4. 5933 1. 8570 x Error Sr = 23. 1082 Correlation Coefficient r = 0. 9617

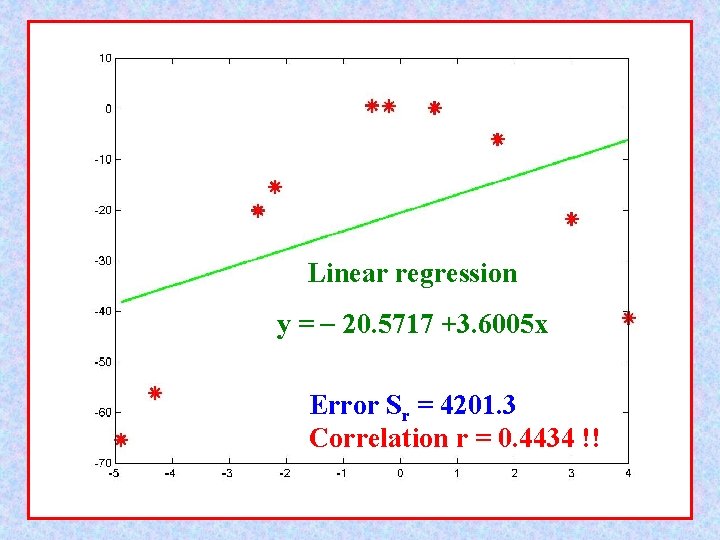
» [x, y]=example 2 x = Columns 1 through 7 -2. 5000 3. 0000 1. 7000 Columns 8 through 10 -2. 2000 -4. 3000 -0. 2000 y = Columns 1 through 7 -20. 1000 -21. 8000 -6. 0000 Columns 8 through 10 -15. 4000 -56. 1000 0. 5000 » s=Linear_LS(x, y) a 0 = -20. 5717 a 1 = 3. 6005 x y -2. 5000 -20. 1000 3. 0000 -21. 8000 1. 7000 -6. 0000 -4. 9000 -65. 4000 0. 6000 0. 2000 -0. 5000 0. 6000 4. 0000 -41. 3000 -2. 2000 -15. 4000 -4. 3000 -56. 1000 -0. 2000 0. 5000 err = 4. 2013 e+003 Syx = 22. 9165 r = 0. 4434 s = -20. 5717 3. 6005 (a 0+a 1*x) -29. 5730 -9. 7702 -14. 4509 -38. 2142 -18. 4114 -22. 3720 -6. 1697 -28. 4929 -36. 0539 -21. 2918 -4. 9000 0. 6000 -0. 5000 4. 0000 Data in arbitrary order -65. 4000 0. 2000 0. 6000 -41. 3000 (y-a 0 -a 1*x) 9. 4730 -12. 0298 8. 4509 -27. 1858 18. 6114 22. 9720 -35. 1303 13. 0929 -20. 0461 21. 7918 Large errors !! Correlation coefficient r = 0. 4434 Linear Least Square: y = 20. 5717 + 3. 6005 x

Linear regression y = 20. 5717 +3. 6005 x Error Sr = 4201. 3 Correlation r = 0. 4434 !!

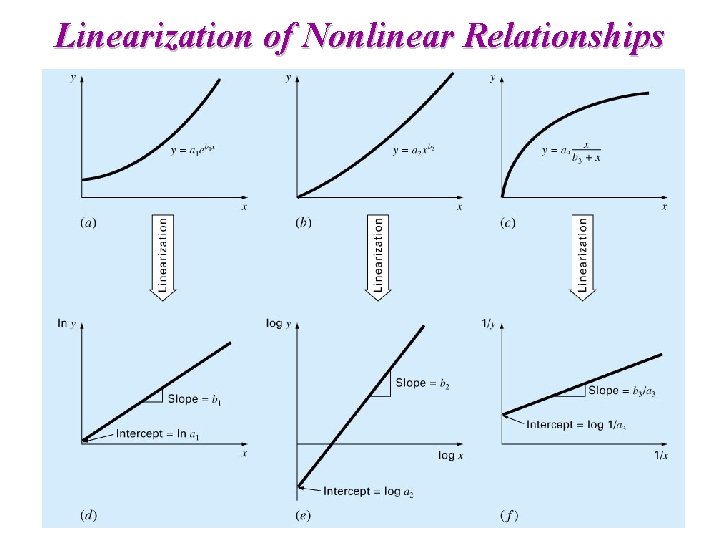
Linearization of Nonlinear Relationships

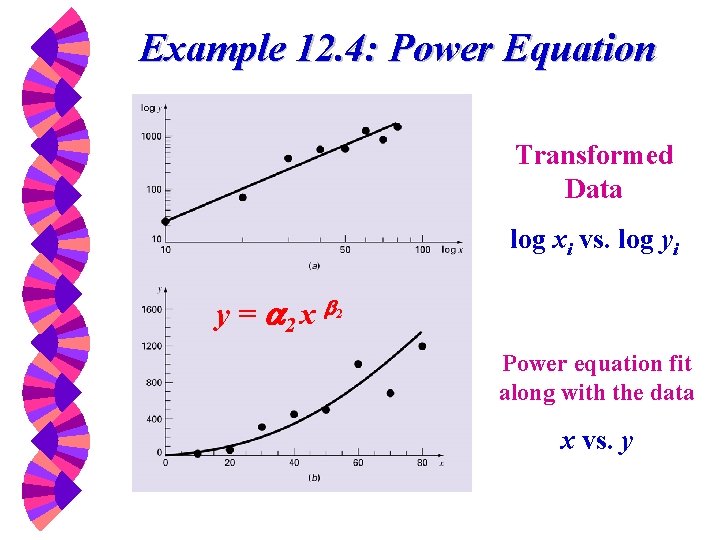
Untransformed power equation x vs. y transformed data log x vs. log y

Linearization of Nonlinear Relationships w Exponential equation w Power equation log : Base-10

Linearization of Nonlinear Relationships w Saturation-growth-rate equation w Rational function

Example 12. 4: Power Equation Transformed Data log xi vs. log yi y = 2 x 2 Power equation fit along with the data x vs. y

>> x=[10 20 30 40 50 60 70 80]; >> y = [25 70 380 550 610 1220 830 1450]; >> [a, r 2] = linregr(x, y) a = 19. 4702 -234. 2857 r 2 = y = 19. 4702 x 234. 2857 0. 8805 12 -12

>> >> >> r 2 x=[10 20 30 40 50 60 70 80]; y = [25 70 380 550 610 1220 830 1450]; linregr(log 10(x), log 10(y)) = log y = 1. 9842 log x – 0. 5620 0. 9481 ans = y = (10– 0. 5620)x 1. 9842 = 0. 2742 x 1. 9842 -0. 5620 log x vs. log y 12 -13

MATLAB Functions w Least-square fit of nth-order polynomial p = polyfit(x, y, n) w Evaluate the value of polynomial using y = polyval(p, x)

CVEN 302 -501 Homework No. 9 Chapter 13 Prob. 13. 1 (20)& 13. 2(20) (Hand Calculations) w Prob. 13. 5 (30) & 13. 7(30) (Hand Calculation and MATLAB program) w You may use spread sheets for your hand computation w w w Due Oct/22, 2008 Wednesday at the beginning of the period