Eulers Method Section 6 6 Suppose we are

Euler’s Method Section 6. 6

Suppose we are given a differential equation and initial condition: Then we can approximate the solution to the differential equation by its linearization (which is “close enough” in a short interval about x 0 ). The basis of Euler’s method is to “string together” many (solution curve) linearizations to approximate a curve.

Now, let’s specify a new value for the independent variable: If dx is small, then we have a new linearization: From the point , which lies exactly on the solution curve, we have obtained the point , which lies very close to the point on the solution curve.

Second Step: We use the point of the solution curve through Setting curve through and the slope. , we use the linearization of the solution to calculate This gives us the next approximation solution curve. to values along the Continue the pattern to find the third approximation: Let’s see this process graphically…

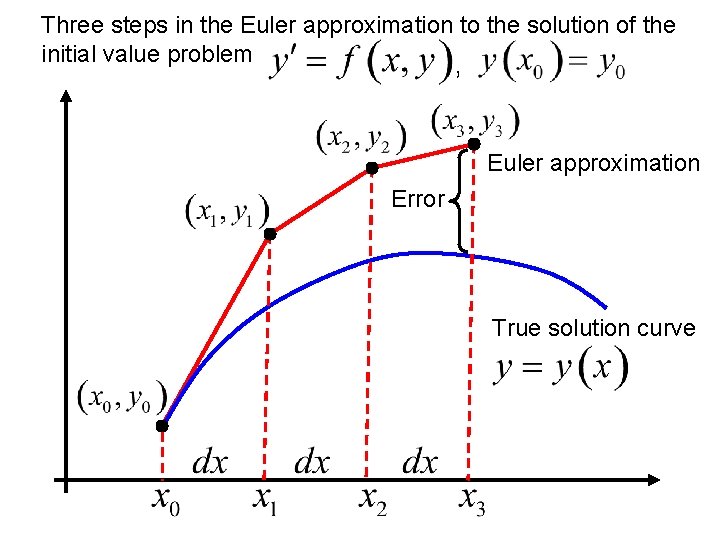
Three steps in the Euler approximation to the solution of the initial value problem , Euler approximation Error True solution curve

Using Euler’s Method Find the first three approximations method for the initial value problem starting at We have: with using Euler’s

Using Euler’s Method Find the first three approximations method for the initial value problem starting at with First Approximation using Euler’s

Using Euler’s Method Find the first three approximations method for the initial value problem starting at with Second Approximation using Euler’s

Using Euler’s Method Find the first three approximations method for the initial value problem starting at with Third Approximation using Euler’s

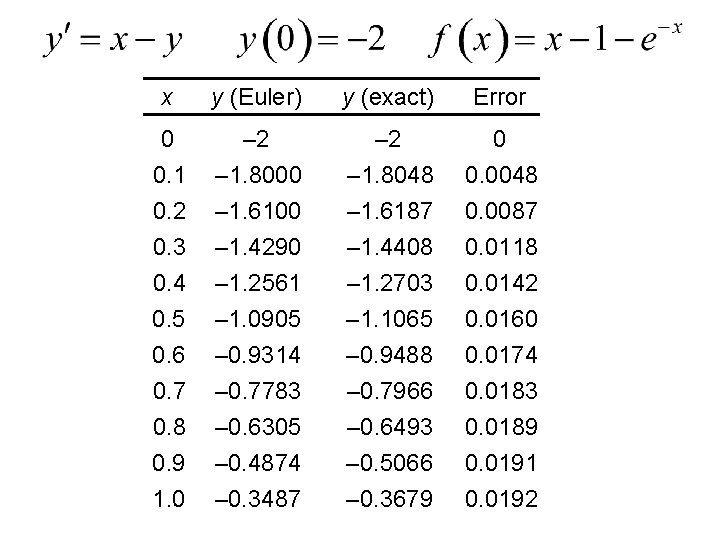
Using Euler’s Method Use Euler’s method to solve the given initial value problem on the interval starting at with. Compare the approximations to the values of the exact solution. Let me show you a new calculator program!!!

x y (Euler) y (exact) Error 0 – 2 0 0. 1 0. 2 0. 3 0. 4 0. 5 0. 6 0. 7 0. 8 0. 9 1. 0 – 1. 8000 – 1. 6100 – 1. 4290 – 1. 2561 – 1. 0905 – 0. 9314 – 0. 7783 – 0. 6305 – 0. 4874 – 0. 3487 – 1. 8048 – 1. 6187 – 1. 4408 – 1. 2703 – 1. 1065 – 0. 9488 – 0. 7966 – 0. 6493 – 0. 5066 – 0. 3679 0. 0048 0. 0087 0. 0118 0. 0142 0. 0160 0. 0174 0. 0183 0. 0189 0. 0191 0. 0192

Other Practice Problems Use differentiation and substitution to show that the given function is the exact solution of the given initial value problem. The same! Initial Condition: The same!

Other Practice Problems Use analytic methods to find the exact solution of the given initial value problem.

Other Practice Problems Use analytic methods to find the exact solution of the given initial value problem. Initial Condition: Solution: or

Other Practice Problems Use analytic methods to find the exact solution of the given initial value problem. Initial Condition: Solution: