Eulers Equation in Fluid Mechanics What is Fluid

Euler’s Equation in Fluid Mechanics

What is Fluid Mechanics? • Fluid mechanics is the study of the macroscopic physical behavior of fluids. • Fluids are specifically liquids and gases though some other materials and systems can be described in a similar way. • Problems involve calculating for various properties of the fluid as functions of space and time, such as: • Velocity • Pressure • Density • Temperature • Fluid dynamics is a branch of fluid mechanics which includes fields from: • aerodynamics (the study of gases in motion) • hydrodynamics (liquids in motion) • These fields are used in calculating forces and moments on aircraft , the mass flow of petroleum through pipelines, and prediction of weather patterns.

Euler’s Differential Equations of Fluid Mechanics ρ = density u = velocity p = pressure γ = Cp / Cv n n n These equations are the very basis of fluid mechanics. This despite, their formulation more than 250 years ago. Here the Cp and the Cv represent the specific heats of the fluid at constant pressure and constant volume, respectively. For steady, isentropic, irrotational, inviscid flow, the transformed equation is linear

Rewriting the above equations in simplified notation, we have: (1) (2) (3) From the third equation we can deduce that if we let then it is automatically satisfied. Further, we can use this relation to simplify the first two equations.

Differentiation and substitution into equations one and two yields For simplicity, since denote it as c. is a constant we will

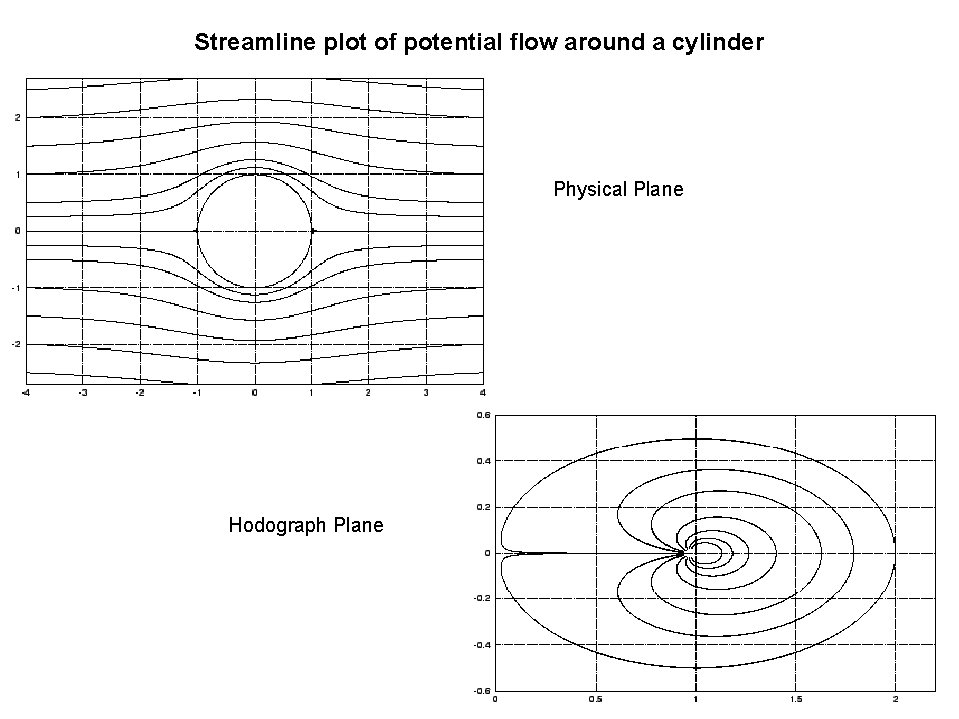
The Hodograph Transformation • A transformation of coordinates used in fluid dynamics. • In the physical plane, the independent variables are the position coordinates x and t. • In the hodograph plane, the independent variables are the components of the velocity vector, ρ and u. • Dependent variables (including position) are determined from the velocity components.

Taking the first equation and applying the Hodograph Transformation we get: Start with the first equation rewritten: Applying the transformation: Resulting in

Now, take the second equation and apply the Hodograph Transformation: Start with the second equation rewritten: Applying the transformation: Resulting in But by multiplying by -1:

Therefore, And assuming that u and p are independent, we can let:

Taking partial derivatives and setting the two equal to each other we then get Which after simplification produces

Streamline plot of potential flow around a cylinder Physical Plane Hodograph Plane

Hodograph Pros and Cons n Pros n n An infinite area in the physical plane maps into a finite area in the hodograph plane. When the flow is steady, isentropic, irrotational, and inviscid, the transformed equation is linear. This is the most important reason for considering the hodograph transformation. n Cons n The transformation is not one-to-one; the fluid that flows above the body, and the fluid that flows below the body usually transform to the same area in the hodograph plane.

Questions