Approximation Algorithms Introduction 2020 09 25 l Approximation

Approximation Algorithms

Introduction 2020 -09 -25 l Approximation algorithms for optimization problems. l Approximation algorithm - an algorithm that is guaranteed to run quickly (in time polynomial in the input size) and to produce a solution for which the value of the objective function is quantifiably close to the optimal value. Dao Thanh Tinh 2

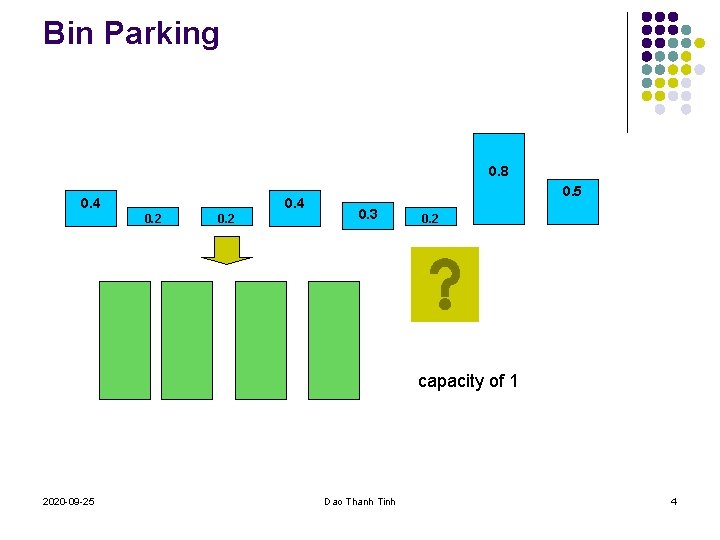
Bin Parking Problem: Given S={s 1, s 2, . . . , sn}, 0<si 1, i=1, 2, . . . , n. How to pack S into as few bins as possible, where which bin has capacity 1. 2020 -09 -25 Dao Thanh Tinh 3

Bin Parking 0. 8 0. 4 0. 2 0. 5 0. 3 0. 2 capacity of 1 2020 -09 -25 Dao Thanh Tinh 4

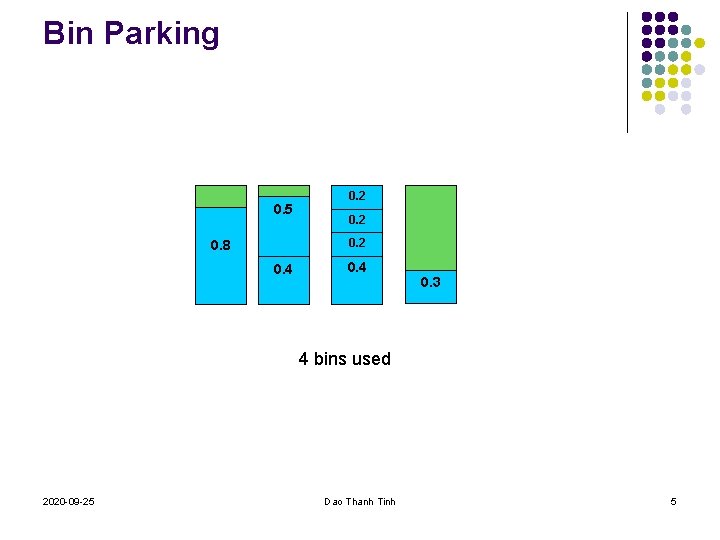
Bin Parking 0. 5 0. 2 0. 8 0. 4 0. 3 4 bins used 2020 -09 -25 Dao Thanh Tinh 5

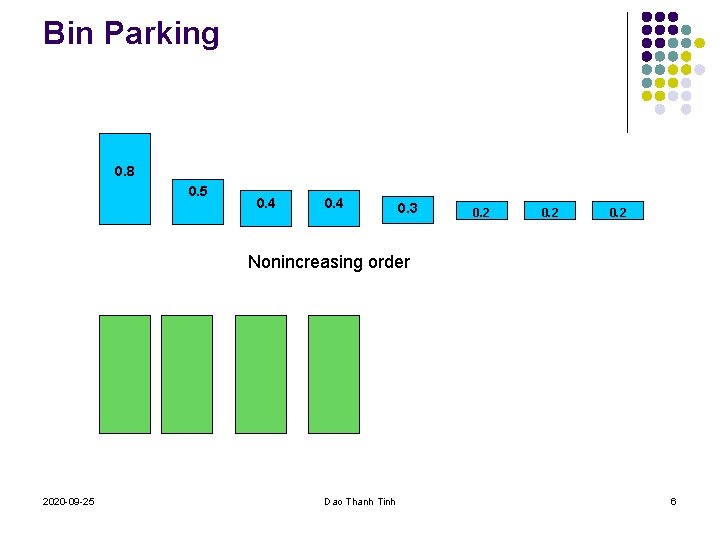
Bin Parking 0. 8 0. 5 0. 4 0. 3 0. 2 Nonincreasing order 2020 -09 -25 Dao Thanh Tinh 6

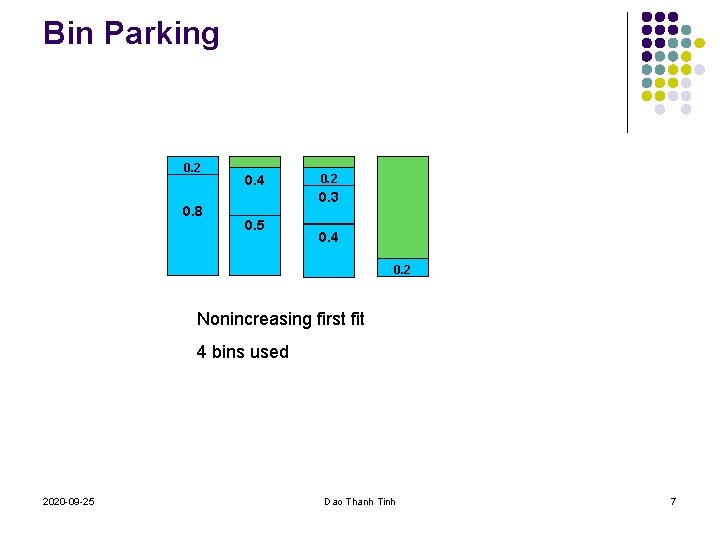
Bin Parking 0. 2 0. 8 0. 4 0. 2 0. 3 0. 5 0. 4 0. 2 Nonincreasing first fit 4 bins used 2020 -09 -25 Dao Thanh Tinh 7

Bin Parking Problem: Given S={s 1, s 2, . . . , sn}, 0< s i T, i = 1, 2, . . . , n. How to pack S into as few bins as possible, where which bin has capacity T. Set yi = 1 if bin i is used, otherwise yi=0. Number of the used bins is Set xij = 1 if item j is put into bin i, otherwise xij=0. An each item can put exactly into only one bin!!! Each bin have capacity T minimize B 2020 -09 -25 Dao Thanh Tinh 8

Bin Parking Problem: Given S={s 1, s 2, . . . , sn}, 0< s i T, i = 1, 2, . . . , n. How to pack S into as few bins as possible, where which bin has capacity T. Nonincreasing first fit (Niff) Input: s(1), s(2), . . . , s(n), 0 < si ≤ 1, i=1, . . , n. Output: An array b(1), . . . , b(n), where b(k)=i if s(k) is placed into bin i. 1) sort s(1) ≥ s(2) ≥. . . ≥ s(n); 2) for (j=1; j≤n; j++) used(j)=0; 3) for (j=1 ; j≤n; j++) i=1; while (used(j)+s(i)>T) do i++; used(i) = used(i) + s(j); b(j) = i; 2020 -09 -25 Dao Thanh Tinh 9

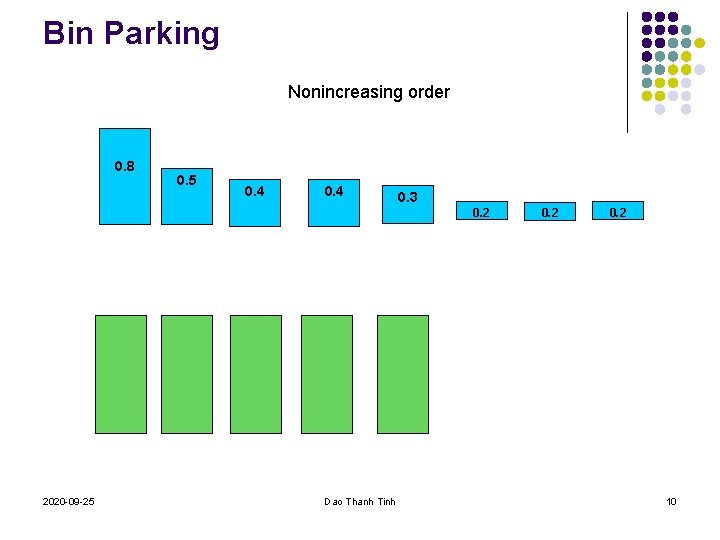
Bin Parking Nonincreasing order 0. 8 0. 5 0. 4 0. 3 0. 2 2020 -09 -25 Dao Thanh Tinh 0. 2 10

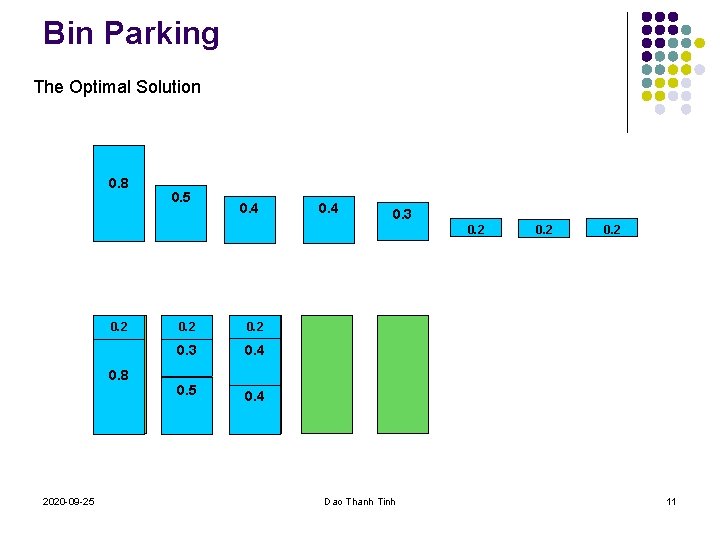
Bin Parking The Optimal Solution 0. 8 0. 5 0. 4 0. 3 0. 2 0. 8 2020 -09 -25 0. 2 0. 3 0. 4 0. 5 0. 4 Dao Thanh Tinh 0. 2 11

Bin Parking The Optimal Solution 0. 2 0. 8 0. 2 0. 3 0. 4 0. 2 0. 8 0. 5 0. 4 0. 2 0. 3 0. 5 0. 4 0. 2 Lemma 1. Let S={s 1, s 2, . . . , sn} - input objects op(S) be the minimum number of bins for S All of the objects placed by Niff in the extra bins have size (weight) at most T/3 (1/3) 2020 -09 -25 Dao Thanh Tinh 12

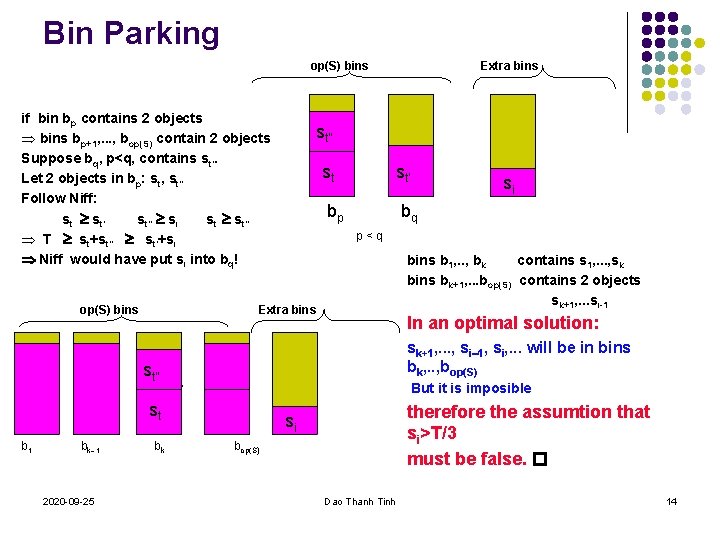
Bin Parking Lemma 1. Let S={s 1, s 2, . . . , sn} - input objects op(S) be the minimum number of bins for S All of the objects placed by Niff in the extra bins have size (weight) at most T/3 (1/3) Proof. Let i is index of the first objects placed by Niff in bin op(S)+1. Suppose that Niff: si>T/3 then: 1) s 1, . . . , si 1>T/3 2) bins bj, j=1, . . , op(S), contain at most 2 objects . . . si op(S) bins 2020 -09 -25 Extra bins Dao Thanh Tinh 13

Bin Parking op(S) bins if bin bp contains 2 objects Þ bins bp+1, . . . , bop(S) contain 2 objects Suppose bq, p<q, contains st’. Let 2 objects in bp: st, st” Follow Niff: st st’ st” si st st” Þ T st+st” st’+si Niff would have put si into bq! op(S) bins 2020 -09 -25 st st’ bp bk si bq p<q bins b 1, . . , bk contains s 1, . . . , sk bins bk+1, . . . bop(S) contains 2 objects sk+1, . . . si-1 In an optimal solution: sk+1, . . . , si 1, si, . . . will be in bins bk, . . , bop(S) . . . But it is imposible st bk 1 st” Extra bins st” b 1 Extra bins therefore the assumtion that si>T/3 must be false. si bop(S) Dao Thanh Tinh 14

Bin Parking op(S) bins Lemma 2. For S={s 1, . . . , sn} Let F(S) is the number of objects which placed in extra bins bop(S)+1, . . . Then F(S) < op(S) Extra bins st” st st’ bp si bq p<q Proof. Suppose that F(S) = op(S) Let: u 1, . . . , uop(S) be the objects which placed into extra bins t 1, . . . , top(S) be the final contents of bins b 1, . . . , bop(S) There are: bj + uj > T, j =1, . . . , op(S) 2020 -09 -25 Dao Thanh Tinh which is impossible 15

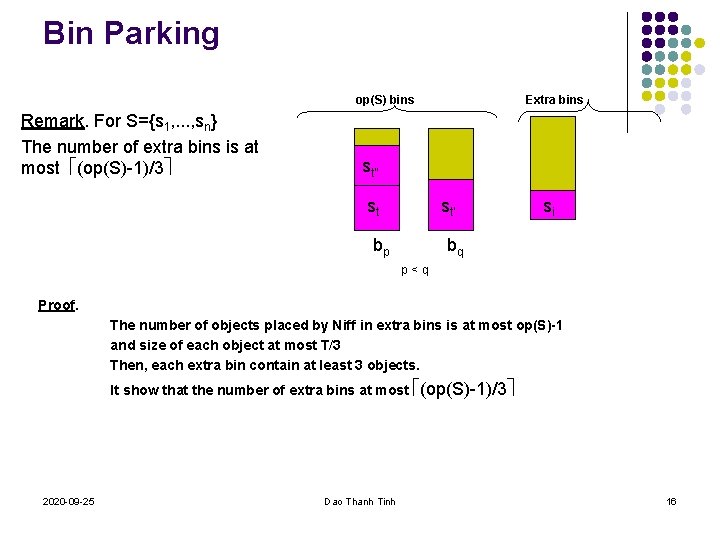
Bin Parking op(S) bins Remark. For S={s 1, . . . , sn} The number of extra bins is at most (op(S)-1)/3 Extra bins st” st st’ bp si bq p<q Proof. The number of objects placed by Niff in extra bins is at most op(S)-1 and size of each object at most T/3 Then, each extra bin contain at least 3 objects. It show that the number of extra bins at most (op(S)-1)/3 2020 -09 -25 Dao Thanh Tinh 16

Stategies Remark. For S={s 1, . . . , sn} The number of extra bins is at most (op(S)-1)/3 Proof. The number of objects placed by Niff in extra bins is at most op(S)-1 and size of each object at most T/3 Then, each extra bin contain at least 3 objects. It show that the number of extra bins at most (op(S)-1)/3 2020 -09 -25 Dao Thanh Tinh 17