INTERPOLATION APPROXIMATION Curve algorithm General curve shape may

INTERPOLATION & APPROXIMATION

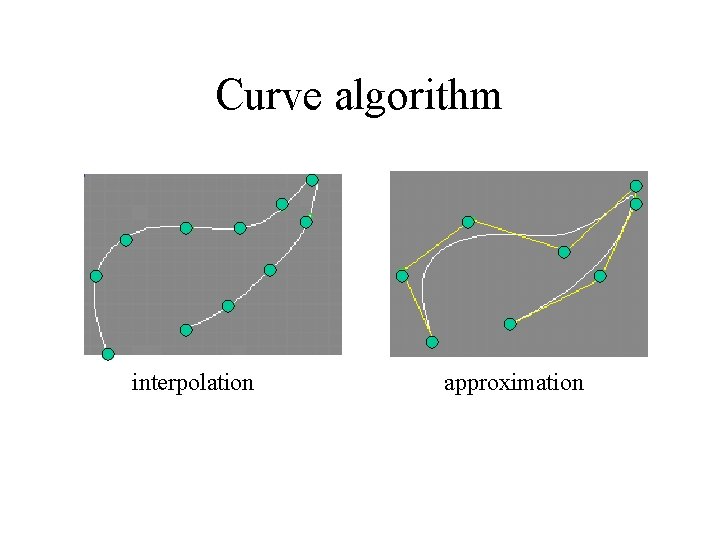
Curve algorithm • General curve shape may be generated using method of – Interpolation (also known as curve fitting) • Curve will pass through control points – Approximation • Curve will pass near control points may interpolate the start and end points.

Curve algorithm interpolation approximation

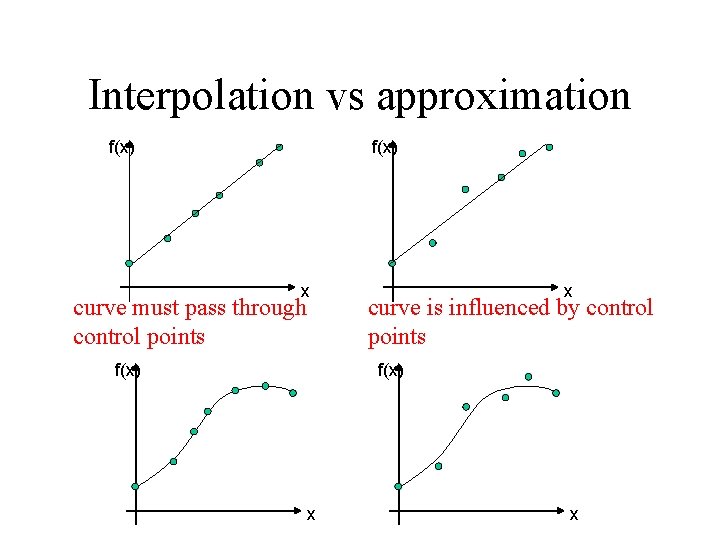
Interpolation vs approximation f(x) x curve must pass through control points f(x) x curve is influenced by control points f(x) x x

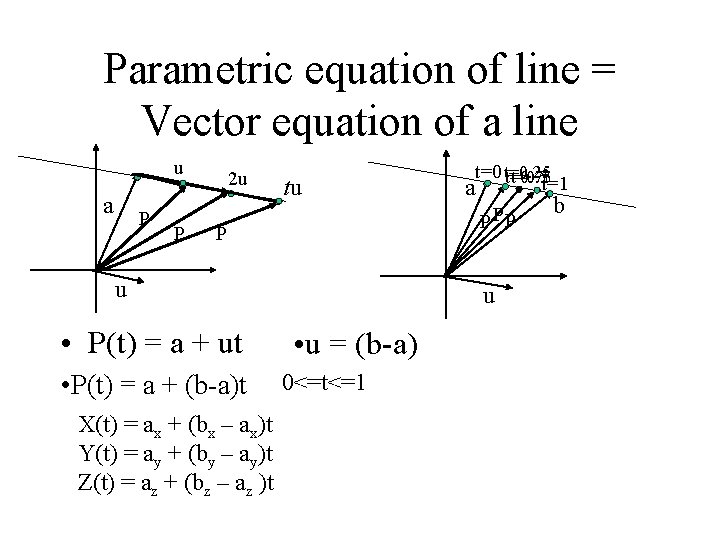
Parametric equation of line = Vector equation of a line u a P P 2 u tu P PP P u • P(t) = a + ut • P(t) = a + (b-a)t X(t) = ax + (bx – ax)t Y(t) = ay + (by – ay)t Z(t) = az + (bz – az )t t=0. 25 t=0. 5 t=1 a t=0. 75 u • u = (b-a) 0<=t<=1 b

Linear interpolation A B t=1 t=0 • P(t) = A(1 -t) + Bt • In matrix form • P(t) = X(t) = A B. -1 1. t Y(t) Z(t) 1 in animation : - path , morphing 0 1

Interpolation Curves • Curve is constrained to pass through all control points • Given points P 0, P 1, . . . Pn, find lowest degree polynomial which passes through the points x(t) = an-1 tn-1 +. . + a 2 t 2 + a 1 t + a 0 y(t) = bn-1 tn-1 +. . + b 2 t 2 + b 1 t + b 0

Interpolating curve : piecewise linear • • Curve defined by multiple segments (linear) Segments joints known as KNOTS Requires too many data points for most shape Representation not flexible enough to editing

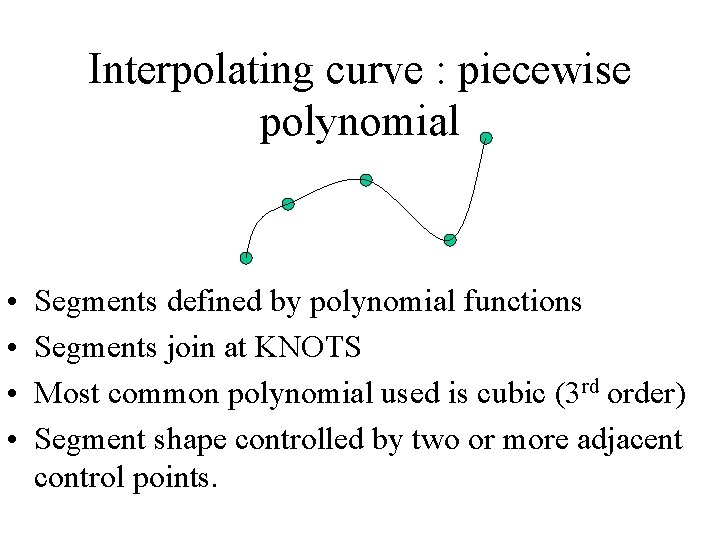
Interpolating curve : piecewise polynomial • • Segments defined by polynomial functions Segments join at KNOTS Most common polynomial used is cubic (3 rd order) Segment shape controlled by two or more adjacent control points.

Knot points • Location where segments join referred to as knots • Knots may or may not coincide with control points in interpolating curves.

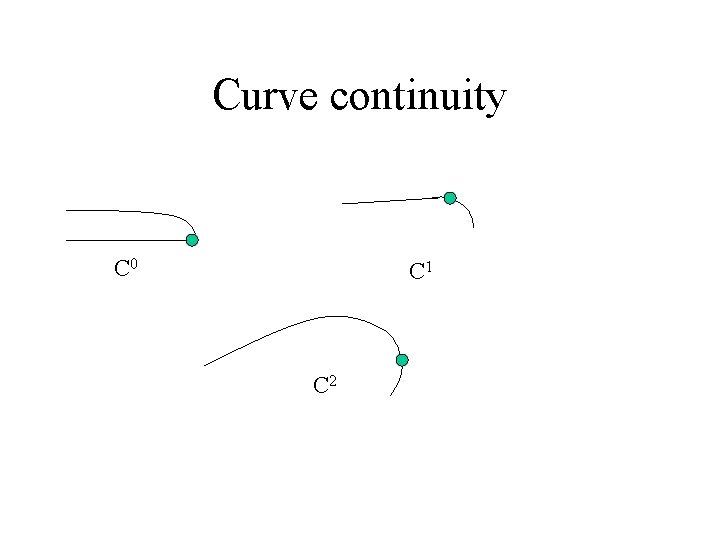
Curve continuity • Concern is continuity at knots. • Continuity conditions – Point continuity (no slope or curvature restriction / no gap) – Tangent continuity (same slope at knot) – Curvature continuity ( same slope and curvature at knot)

Curve continuity • Continuity - Cn – C 0 continuity – continuity of endpoint only or continuity of position. – C 1 continuity is tangent continuity or first derivative of position – C 2 continuity is curvature continuity or second derivative of position.

Curve continuity C 0 C 1 C 2

Interpolation curves • Typically possess curvature continuity • Shape defined by – Endpoint and control point location – Tangent vectors at knots – Curvature at knots

Interpolation vs. Approximation Curves • Interpolation Curve – over constrained → lots of (undesirable? ) oscillations • Approximation Curve – more reasonable?

Approximation techniques • Developed to permit greater design flexibility in the generation of free form curves • Common methods in modern CAD systems, bezier, b-spline, NURBS • Employ control points (set of vertices that approximate the curve)

Approximation techniques • Curves do not pass directly through points (except start and end) • Intermediate points affect shape as if exerting a “pull” on the curve. • Allow user to set shape by “pulling” out curve using control point location.

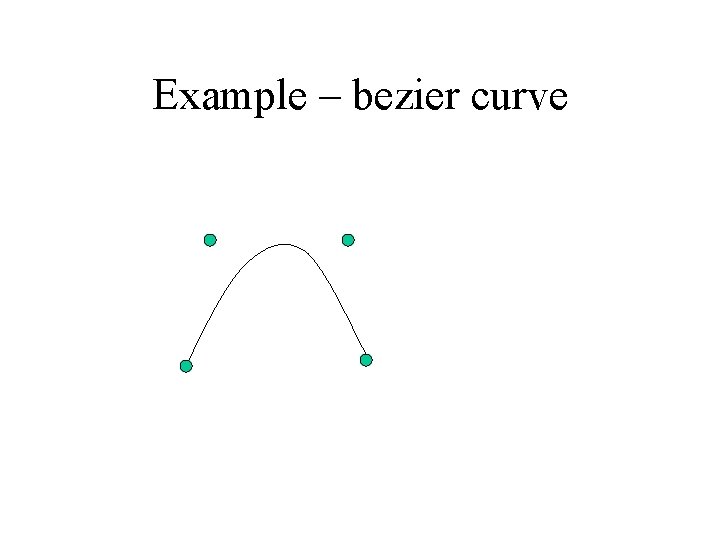
Example – bezier curve

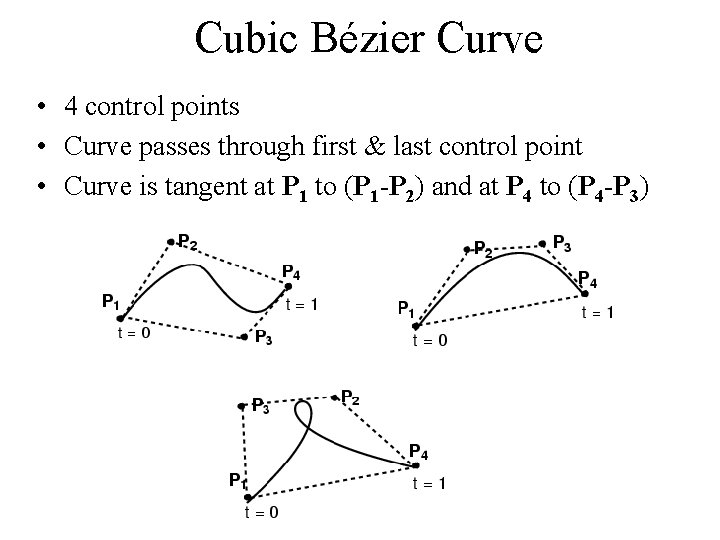
Cubic Bézier Curve • 4 control points • Curve passes through first & last control point • Curve is tangent at P 1 to (P 1 -P 2) and at P 4 to (P 4 -P 3)