1 Decision Science Chapter 5 An introduction to




















- Slides: 35

1 Decision Science Chapter 5 An introduction to Transportation Models © 2008 Prentice-Hall, Inc.

Introduction n Transportation model n The transportation problem deals with the distribution of goods from several points of supply (sources) sources to a number of points of demand (destinations) destinations n Usually we are given the capacity of goods at each source and the requirements at each destination n Typically the objective is to minimize total transportation and production costs © 2009 Prentice-Hall, Inc. 10 – 2

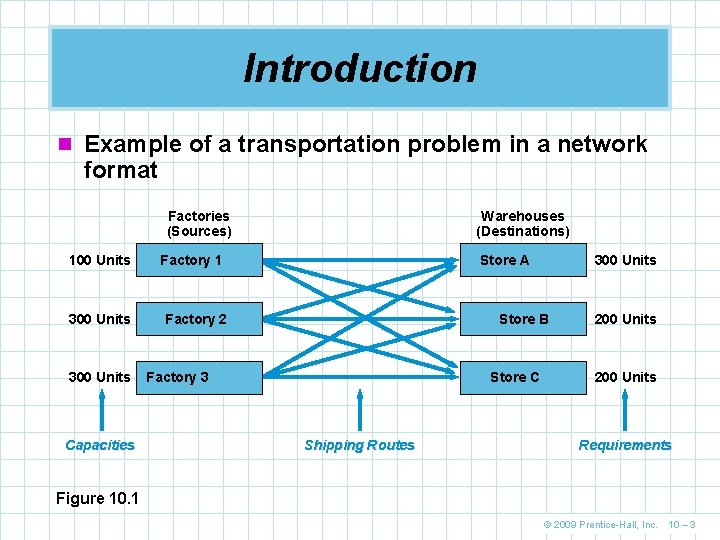
Introduction n Example of a transportation problem in a network format Factories (Sources) 100 Units 300 Units Capacities Warehouses (Destinations) Factory 1 Store A Factory 2 300 Units Store B Factory 3 Store C Shipping Routes 200 Units Requirements Figure 10. 1 © 2009 Prentice-Hall, Inc. 10 – 3

Introduction n Assignment model n The assignment problem refers to the class of LP problems that involve determining the most efficient assignment of resources to tasks n The objective is most often to minimize total costs or total time to perform the tasks at hand n One important characteristic of assignment problems is that only one job or worker can be assigned to one machine or project © 2009 Prentice-Hall, Inc. 10 – 4

Setting Up a Transportation Problem n The Executive Furniture Corporation manufactures office desks at three locations: Factory 1, Factory 2 and Factory 3 n The firm distributes the desks through regional warehouses located in Store A, Store B and Store C n Estimates of the monthly production capacity of each factory and the desks needed at each warehouse are shown in the following Figure © 2009 Prentice-Hall, Inc. 10 – 5

Setting Up a Transportation Problem n Production costs are the same at the three factories so the only relevant costs are shipping from each source to each destination n Costs are constant no matter the quantity shipped n The transportation problem can be described as how to select the shipping routes to be used and the number of desks to be shipped on each route so as to minimize total transportation cost n Restrictions regarding factory capacities and warehouse requirements must be observed © 2009 Prentice-Hall, Inc. 10 – 6

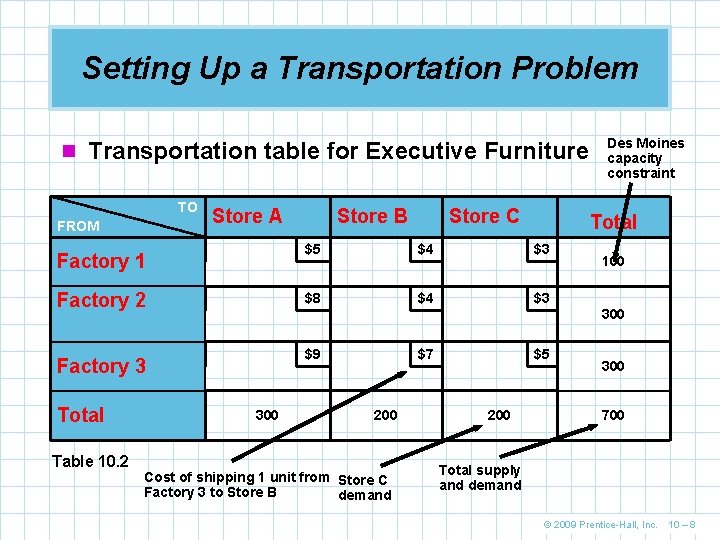
Setting Up a Transportation Problem n The first step is setting up the transportation table n Its purpose is to summarize all the relevant data and keep track of algorithm computations Transportation costs per desk for Executive Furniture TO FROM Store A Store B Store C Factory 1 $5 $4 $3 Factory 2 $8 $4 $3 Factory 3 $9 $7 $5 © 2009 Prentice-Hall, Inc. 10 – 7

Setting Up a Transportation Problem n Transportation table for Executive Furniture TO FROM Store A Factory 1 Factory 2 Factory 3 Total Table 10. 2 300 Store B Store C Total $5 $4 $3 $8 $4 $3 $9 $7 $5 200 Cost of shipping 1 unit from Store C Factory 3 to Store B demand 200 Des Moines capacity constraint 100 300 700 Total supply and demand © 2009 Prentice-Hall, Inc. 10 – 8

Setting Up a Transportation Problem n In this table, total factory supply exactly equals total warehouse demand n When equal demand supply occur, a balanced problem is said to exist n This is uncommon in the real world and we have techniques to deal with unbalanced problems © 2009 Prentice-Hall, Inc. 10 – 9

Developing an Initial Solution: Northwest Corner Rule n Once we have arranged the data in a table, we must establish an initial feasible solution n One systematic approach is known as the northwest corner rule n Start in the upper left-hand cell and allocate units to shipping routes as follows 1. Exhaust the supply (factory capacity) of each row before moving down to the next row 2. Exhaust the demand (warehouse) requirements of each column before moving to the right to the next column 3. Check that all supply and demand requirements are met. n In this problem it takes five steps to make the initial shipping assignments © 2009 Prentice-Hall, Inc. 10 – 10

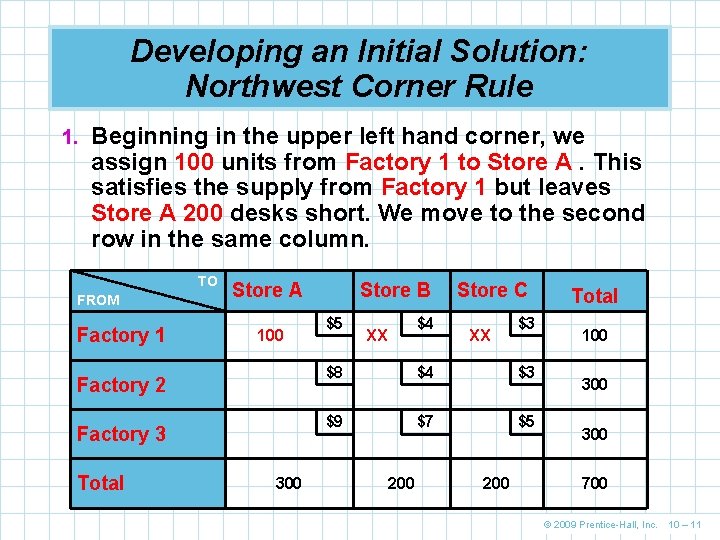
Developing an Initial Solution: Northwest Corner Rule 1. Beginning in the upper left hand corner, we assign 100 units from Factory 1 to Store A. This satisfies the supply from Factory 1 but leaves Store A 200 desks short. We move to the second row in the same column. TO FROM Factory 1 Store A 100 Factory 2 Factory 3 Total 300 Store B $5 $4 XX Store C XX $3 $8 $4 $3 $9 $7 $5 200 Total 100 300 700 © 2009 Prentice-Hall, Inc. 10 – 11

Developing an Initial Solution: Northwest Corner Rule 2. Assign 200 units from Factory 2 to Store A. This meets the demand of Store A. TO FROM Store A Factory 1 100 Factory 2 200 Factory 3 Total XX 300 Store B $5 XX $4 Store C XX $3 $8 $4 $3 $9 $7 $5 200 Total 100 300 700 © 2009 Prentice-Hall, Inc. 10 – 12

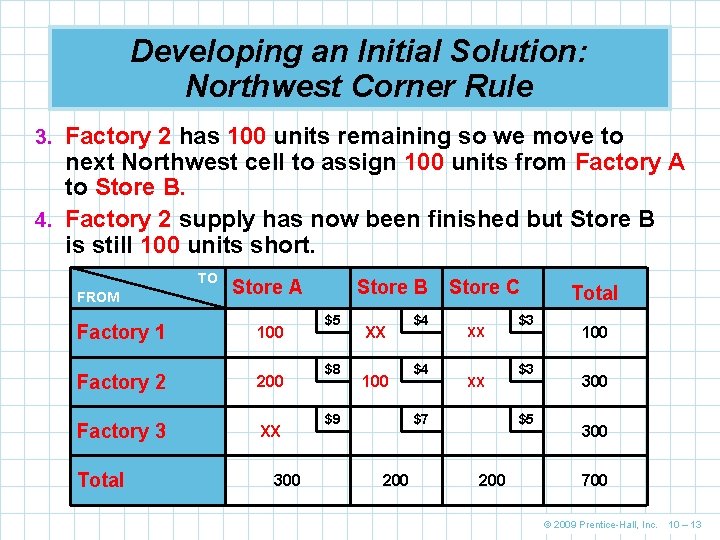
Developing an Initial Solution: Northwest Corner Rule 3. Factory 2 has 100 units remaining so we move to next Northwest cell to assign 100 units from Factory A to Store B. 4. Factory 2 supply has now been finished but Store B is still 100 units short. TO FROM Store A Factory 1 100 Factory 2 200 Factory 3 Total XX 300 Store B $5 $8 XX 100 $9 $4 $4 Store C XX XX $7 200 $3 $3 $5 200 Total 100 300 700 © 2009 Prentice-Hall, Inc. 10 – 13

Developing an Initial Solution: Northwest Corner Rule 4. Assign 100 units from Factory 3 to Store B. This fulfills the demand of Store B. Factory 3 still has 200 units available. TO FROM Factory 1 100 Factory 2 200 Factory 3 XX Total Store B Store A 300 $5 $8 $9 XX 100 200 Store C $4 $4 XX XX $7 Total $3 $3 $5 200 100 300 700 © 2009 Prentice-Hall, Inc. 10 – 14

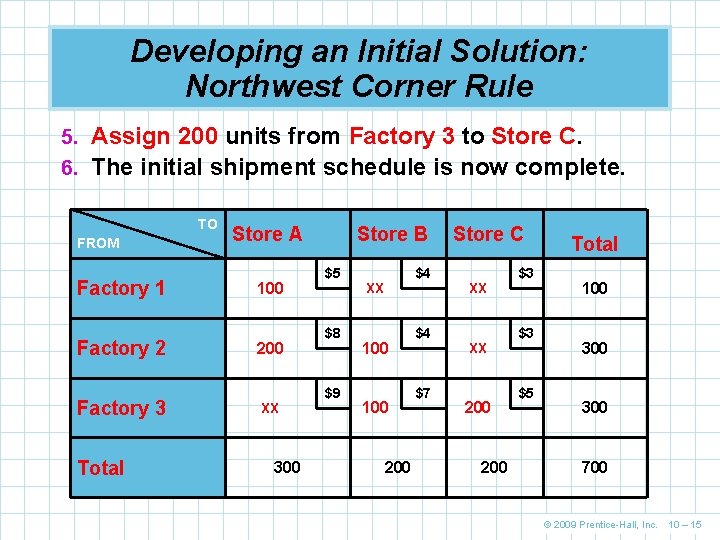
Developing an Initial Solution: Northwest Corner Rule 5. Assign 200 units from Factory 3 to Store C. 6. The initial shipment schedule is now complete. TO FROM Factory 1 Factory 2 Factory 3 Total Store A 100 200 XX 300 Store B $5 $8 $9 XX 100 200 $4 $4 $7 Store C XX XX 200 $3 $3 $5 Total 100 300 700 © 2009 Prentice-Hall, Inc. 10 – 15

Developing an Initial Solution: Northwest Corner Rule n We can easily compute the cost of this shipping assignment ROUTE UNITS SHIPPED PER UNIT x COST ($) TOTAL COST ($) FROM TO 1 A 100 5 500 2 A 200 8 1, 600 2 B 100 4 400 3 B 100 7 700 3 C 200 5 1, 000 = 4, 200 n This solution is feasible but we need to check to see if it is optimal © 2009 Prentice-Hall, Inc. 10 – 16

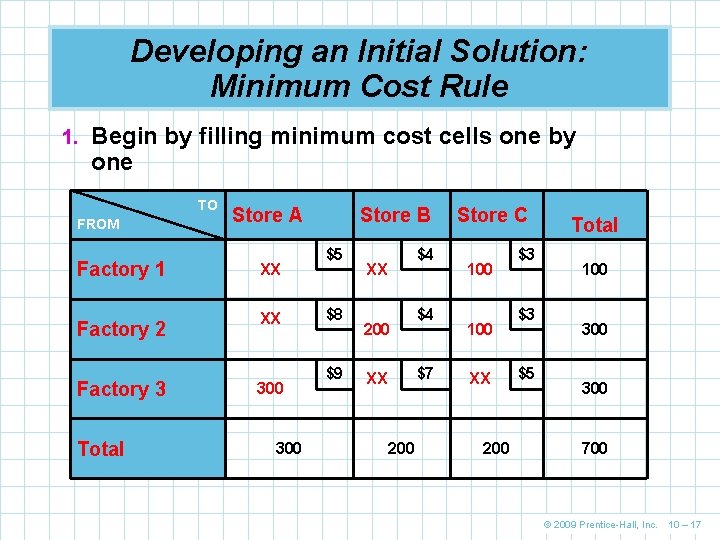
Developing an Initial Solution: Minimum Cost Rule 1. Begin by filling minimum cost cells one by one TO FROM Factory 1 Factory 2 Factory 3 Total Store A XX XX 300 Store B $5 $8 $9 $4 XX 200 $4 $7 XX 200 Store C 100 XX 200 $3 $3 $5 Total 100 300 700 © 2009 Prentice-Hall, Inc. 10 – 17

Developing an Initial Solution: Minimum Cost Rule n We can easily compute the cost of this shipping assignment UNITS SHIPPED PER UNIT x COST ($) = TOTAL COST ($) 100 3 300 200 4 800 300 9 2700 4, 100 n This solution is feasible but we need to check to see if it is optimal © 2009 Prentice-Hall, Inc. 10 – 18

Vogel’s Approximation Method: To Find An Initial Solution n Vogel’s Approximation Method (VAM) VAM is not as simple as the northwest corner method, but it provides a very good initial solution, often one that is the optimal solution n VAM tackles the problem of finding a good initial solution by taking into account the costs associated with each route alternative n This is something that the northwest corner rule does not do n To apply VAM, we first compute for each row and column the penalty faced if we should ship over the second-best route instead of the least-cost route © 2009 Prentice-Hall, Inc. 10 – 19

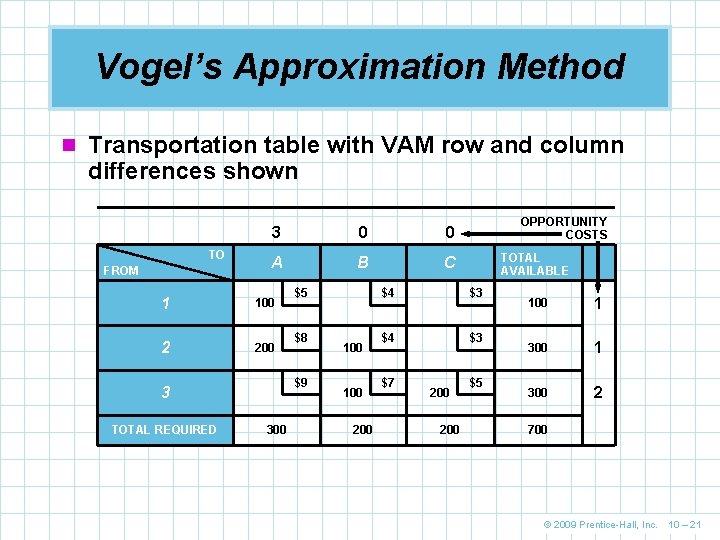
Vogel’s Approximation Method n The six steps involved in determining an initial VAM solution are illustrated below beginning with the same layout originally shown in Table 10. 2 VAM Step 1. 1 For each row and column of the transportation table, find the difference between the distribution cost on the best route in the row or column and the second best route in the row or column n This is the opportunity cost of not using the best route n Step 1 has been done in Table © 2009 Prentice-Hall, Inc. 10 – 20

Vogel’s Approximation Method n Transportation table with VAM row and column differences shown TO FROM 3 0 0 A B C 1 100 2 200 $8 $9 3 TOTAL REQUIRED $5 300 100 200 OPPORTUNITY COSTS TOTAL AVAILABLE $4 $3 $7 200 $5 100 1 300 2 700 © 2009 Prentice-Hall, Inc. 10 – 21

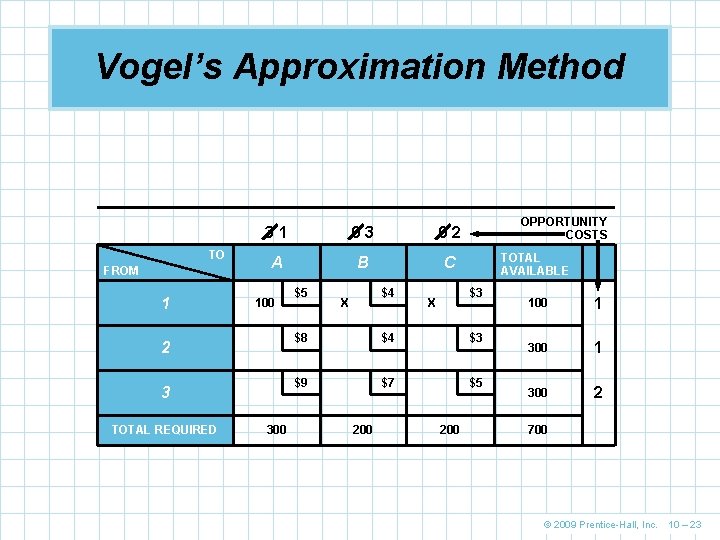
Vogel’s Approximation Method VAM Step 2. 2 identify the row or column with the greatest opportunity cost, or difference (column A in this example) VAM Step 3. Assign as many units as possible to the 3 lowest-cost square in the row or column selected VAM Step 4. 4 Eliminate any row or column that has been completely satisfied by the assignment just made by placing Xs in each appropriate square VAM Step 5. 5 Recompute the cost differences for the transportation table, omitting rows or columns eliminated in the previous step © 2009 Prentice-Hall, Inc. 10 – 22

Vogel’s Approximation Method TO FROM 1 31 03 02 A B C 100 2 3 TOTAL REQUIRED 300 $5 $4 X OPPORTUNITY COSTS TOTAL AVAILABLE $3 X $8 $4 $3 $9 $7 $5 200 100 1 300 2 700 © 2009 Prentice-Hall, Inc. 10 – 23

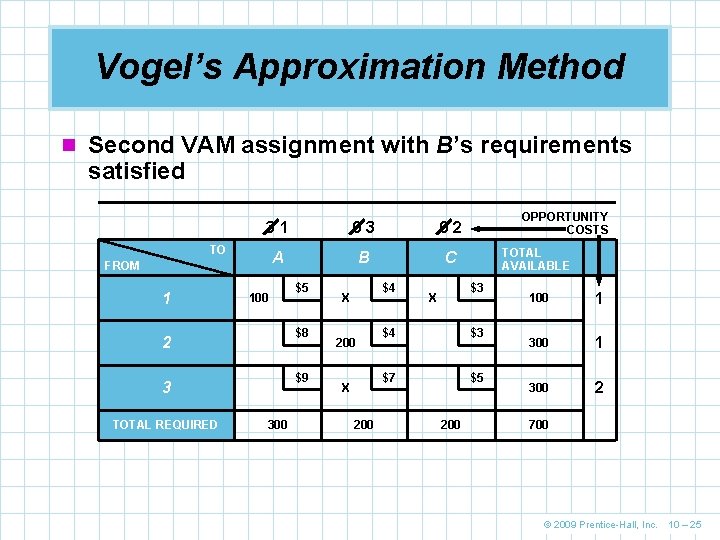
Vogel’s Approximation Method VAM Step 6. 6 Return to step 2 for the rows and columns remaining and repeat the steps until an initial feasible solution has been obtained n In this case column B now has the greatest difference, 3 n We assign 200 units to the lowest-cost square in the column, B n We recompute the differences and find the greatest difference is now in row 2 n We assign 100 units to the lowest-cost square in the column, C © 2009 Prentice-Hall, Inc. 10 – 24

Vogel’s Approximation Method n Second VAM assignment with B’s requirements satisfied 31 03 02 A B C TO FROM 1 100 $8 2 $9 3 TOTAL REQUIRED $5 300 $4 X 200 OPPORTUNITY COSTS TOTAL AVAILABLE $3 X $4 $3 $7 $5 200 1 300 2 700 © 2009 Prentice-Hall, Inc. 10 – 25

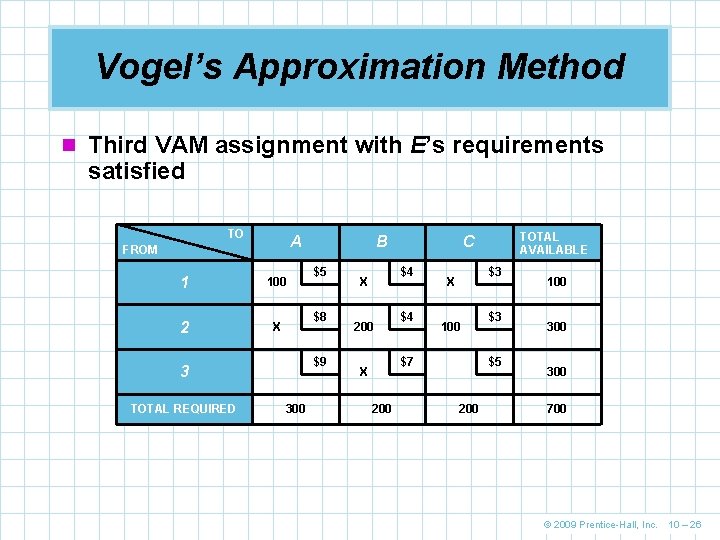
Vogel’s Approximation Method n Third VAM assignment with E’s requirements satisfied TO A FROM 1 100 2 X $5 $8 $9 3 TOTAL REQUIRED B 300 $4 X 200 $4 $3 X 100 $7 X 200 TOTAL AVAILABLE C $3 $5 200 100 300 700 © 2009 Prentice-Hall, Inc. 10 – 26

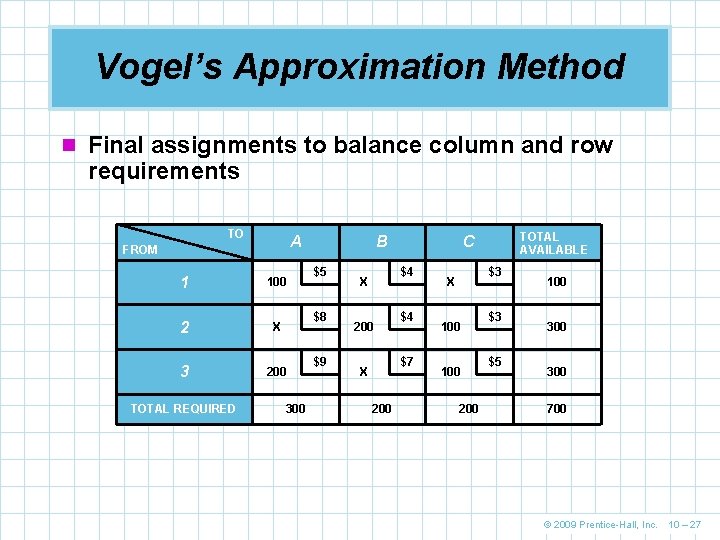
Vogel’s Approximation Method n Final assignments to balance column and row requirements TO A FROM 1 100 2 X 3 200 TOTAL REQUIRED B $5 $8 300 $9 $4 X 200 $4 $7 X 200 TOTAL AVAILABLE C $3 X 100 200 $3 $5 100 300 700 © 2009 Prentice-Hall, Inc. 10 – 27

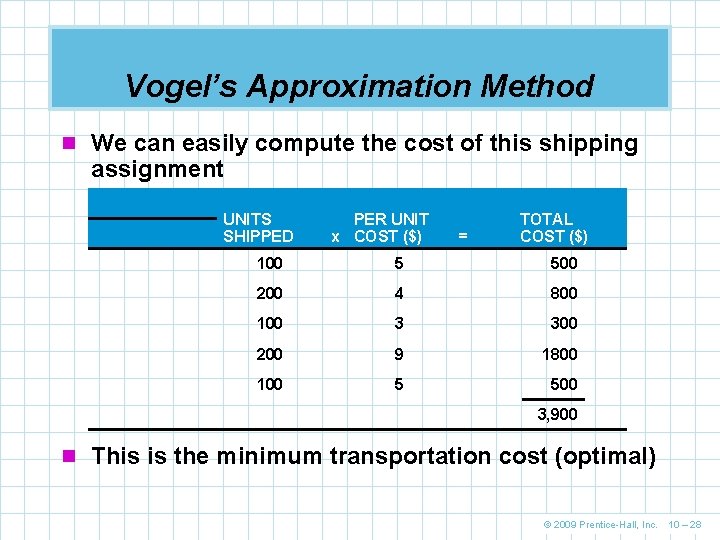
Vogel’s Approximation Method n We can easily compute the cost of this shipping assignment UNITS SHIPPED PER UNIT x COST ($) = TOTAL COST ($) 100 5 500 200 4 800 100 3 300 200 9 1800 100 5 500 3, 900 n This is the minimum transportation cost (optimal) © 2009 Prentice-Hall, Inc. 10 – 28

Unbalanced Transportation Problems n In real-life problems, total demand is frequently not equal to total supply n These unbalanced problems can be handled easily by introducing dummy sources or dummy destinations n If total supply is greater than total demand, a dummy destination (warehouse), with demand exactly equal to the surplus, is created n If total demand is greater than total supply, we introduce a dummy source (factory) with a supply equal to the excess of demand over supply © 2009 Prentice-Hall, Inc. 10 – 29

Unbalanced Transportation Problems n In either case, shipping cost coefficients of zero are assigned to each dummy location or route as no goods will actually be shipped n Any units assigned to a dummy destination represent excess capacity n Any units assigned to a dummy source represent unmet demand © 2009 Prentice-Hall, Inc. 10 – 30

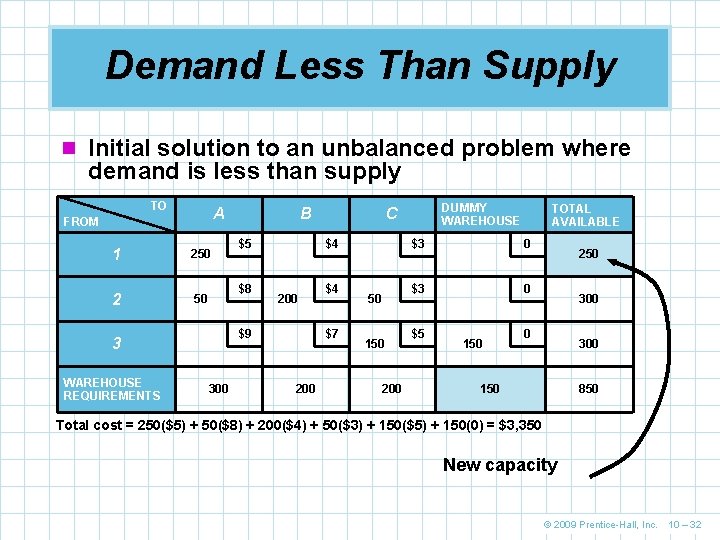
Demand Less Than Supply n Suppose that the Des Moines factory increases its n n n rate of production from 100 to 250 desks The firm is now able to supply a total of 850 desks each period Warehouse requirements remain the same (700) so the row and column totals do not balance We add a dummy column that will represent a fake warehouse requiring 150 desks This is somewhat analogous to adding a slack variable We use the northwest corner rule © 2009 Prentice-Hall, Inc. 10 – 31

Demand Less Than Supply n Initial solution to an unbalanced problem where demand is less than supply TO A FROM 1 250 2 50 $5 $8 200 300 $4 $7 200 DUMMY WAREHOUSE C $4 $9 3 WAREHOUSE REQUIREMENTS B 50 150 200 TOTAL AVAILABLE $3 0 $5 150 250 300 150 850 Total cost = 250($5) + 50($8) + 200($4) + 50($3) + 150($5) + 150(0) = $3, 350 New capacity © 2009 Prentice-Hall, Inc. 10 – 32

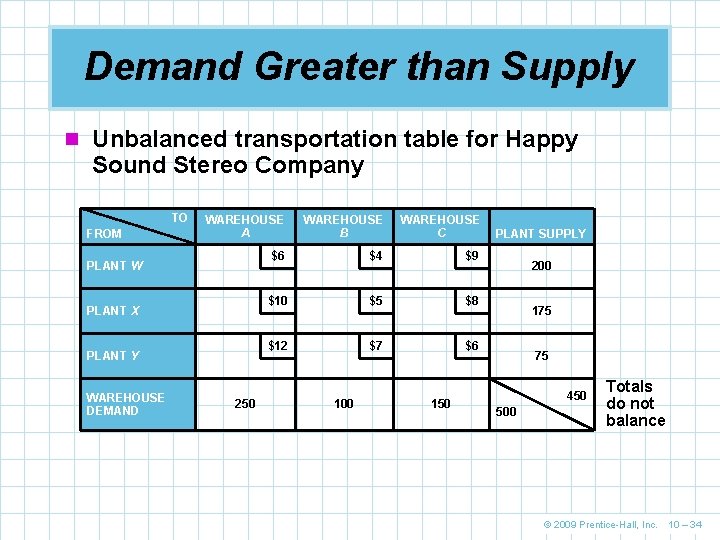
Demand Greater than Supply n The second type of unbalanced condition occurs when total demand is greater than total supply n In this case we need to add a dummy row representing a fake factory n The new factory will have a supply exactly equal to the difference between total demand total real supply n The shipping costs from the dummy factory to each destination will be zero © 2009 Prentice-Hall, Inc. 10 – 33

Demand Greater than Supply n Unbalanced transportation table for Happy Sound Stereo Company TO FROM WAREHOUSE A WAREHOUSE B WAREHOUSE C $6 $4 $9 $10 $5 $8 $12 $7 $6 PLANT W PLANT X PLANT Y WAREHOUSE DEMAND 250 100 150 PLANT SUPPLY 200 175 75 450 500 Totals do not balance © 2009 Prentice-Hall, Inc. 10 – 34

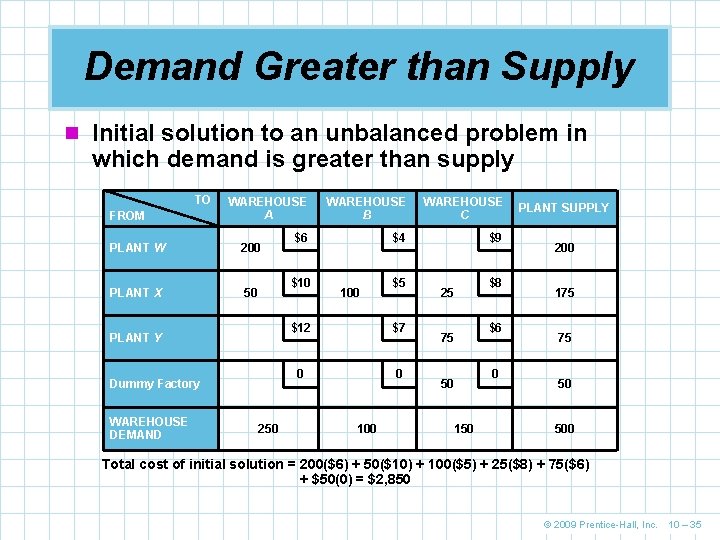
Demand Greater than Supply n Initial solution to an unbalanced problem in which demand is greater than supply TO FROM WAREHOUSE A WAREHOUSE B WAREHOUSE C $6 $4 $9 PLANT W 200 PLANT X 50 $10 PLANT Y Dummy Factory WAREHOUSE DEMAND 250 100 $5 $12 $7 0 0 100 $8 25 $6 75 0 50 150 PLANT SUPPLY 200 175 75 50 500 Total cost of initial solution = 200($6) + 50($10) + 100($5) + 25($8) + 75($6) + $50(0) = $2, 850 © 2009 Prentice-Hall, Inc. 10 – 35