Secure Efficient Multiparty Computing of Multivariate Polynomials and

Secure Efficient Multiparty Computing of Multivariate Polynomials and Applications Dana Dachman-Soled, Tal Malkin, Mariana Raykova, Moti Yung

x 1 x 2 x 3 x 4 2

x 1 F 1(x 1, x 3) x 2 x 3 F 2(x 1, x 3) F 4(x 1, x 3) F 3(x 1, x 3) x 4 3

Secure Multiparty Computation How to compute a function on the private inputs of multiple parties not leaking more than the result? 4

Secure Multiparty Computation Feasible – [Yao 82], [GMW 87], [CDv 88], [BG 89], [BG 90], [Cha 90], [Bea 92], … Not Efficient – communication and computation proportional to circuit size 5

x 1 Multivariate Polynomials x 2 x 3 x 4 6

x 1 Multivariate Polynomials x 3 x 2 Applications x 4 7

Multiparty Set Intersection x 1 Multivariate Polynomials x 3 x 2 Applications x 4 8

x 1 Multivariate Polynomials x 3 x 2 Applications x 4 Linear Algebra matrix arithmetic, inverse, determinant, Eigen values 9

x 1 Multivariate Polynomials x 3 x 2 Applications Statistics functions x 4 average, standard deviation, variance, chi-square test, computing Pearson’s correlation coefficients 10

Taylor series approximation trigonometric functions, logarithms, exponents, square root x 1 Multivariate Polynomials x 3 x 2 Applications x 4 11

Outsourced computation • • many workers at least one honest 12

Outsourced computation • Computation on shares, • Reconstruction of output 13

Our results • Multiparty computation protocol for functionalities that can be represented as multivariate polynomials – Improvement of generic complexity for multiple parties Left as open problem in FM 10 • Security: – Against malicious majority – Proofs in the standard simulation model • Black box construction from homomorphic encryption with a natural property…. – Instantiated through threshold Paillier encryption (decisional composite residuosity) 14

Our Results • Efficiency: – Communication complexity – FM 10 subexponential in the number of parties, we achieve fully polynomial (in all parameters) complexity: • Broadcast complexity • Round table complexity – Constant number round table rounds • Application construction: Multiparty Set Intersection – Improve complexity of existing multiparty solutions KS 05, SS 09, CJS 10 15

Building Blocks • Input sharing using committed Shamir/Reed. Solomon codes PX(0) = X shares PX(1), …, PX(D) • Vector Homomorphic Encryption ENC(m 1; r 1) ⊗ ENC(m 2; r 2) = ENC(m 1 + m 2; r 1 ⊕ r 2) ENC(m; r)c = ENC(c · m; r ⊙ c) – Instantiation: threshold Paillier encryption 16

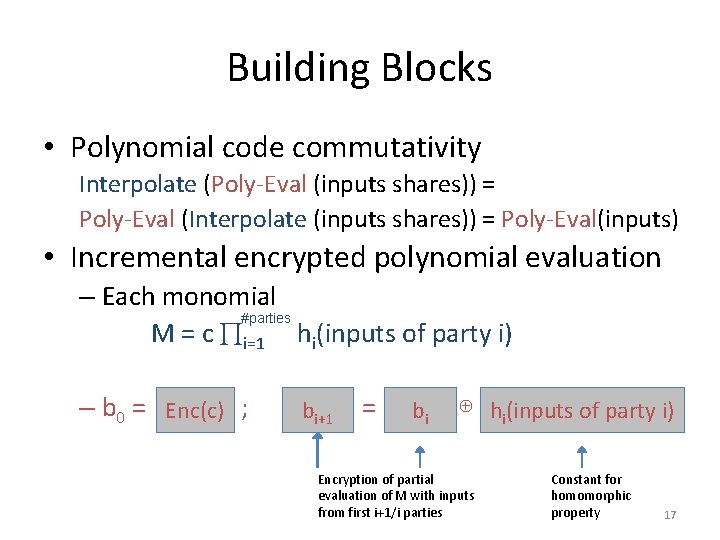
Building Blocks • Polynomial code commutativity Interpolate (Poly-Eval (inputs shares)) = Poly-Eval (Interpolate (inputs shares)) = Poly-Eval(inputs) • Incremental encrypted polynomial evaluation – Each monomial #parties M = c i=1 hi(inputs of party i) – b 0 = Enc(c) ; bi+1 = bi ⊕ hi(inputs of party i) Encryption of partial evaluation of M with inputs from first i+1/i parties Constant for homomorphic property 17

Building blocks • Lagrange Interpolation Protocol Over Encrypted Values: – given A > d+1 encrypted points (1, ENCpk(y 1, r 1)), . . . (A, ENCpk(y. A, r. A)) – check that they lie on poly of degree d d+1 ENCpk(yi, ri) = j=1 (ENCpk(yj, rj)) Lj(i) – synchronized randomness • Randomness Interpolation – given (1, y 1), . . . , (A, y. A), r 1, . . . , rd+1 – compute rd+2, . . . , r. A – Encrypted interpolation holds for [i, ENCpk(yi, ri)]1≤i≤A 18

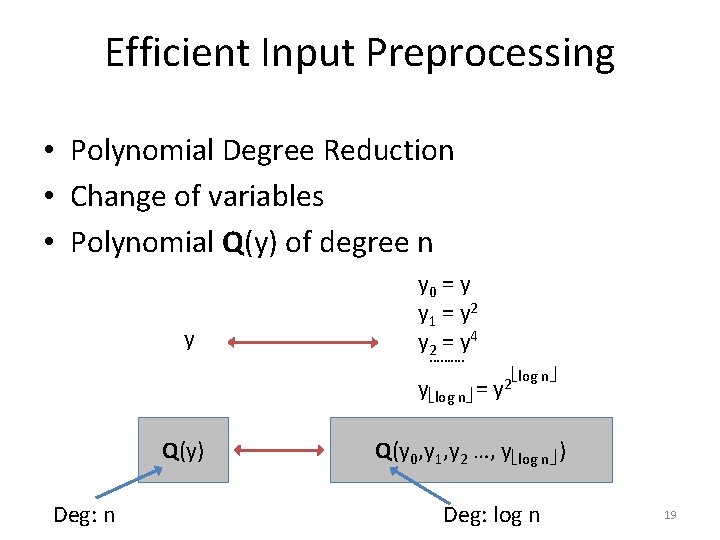
Efficient Input Preprocessing • Polynomial Degree Reduction • Change of variables • Polynomial Q(y) of degree n y y 0 = y y 1 = y 2 = y 4 ………. y log n = Q(y) Deg: n y 2 log n Q(y 0, y 1, y 2 …, y log n ) Deg: log n 19

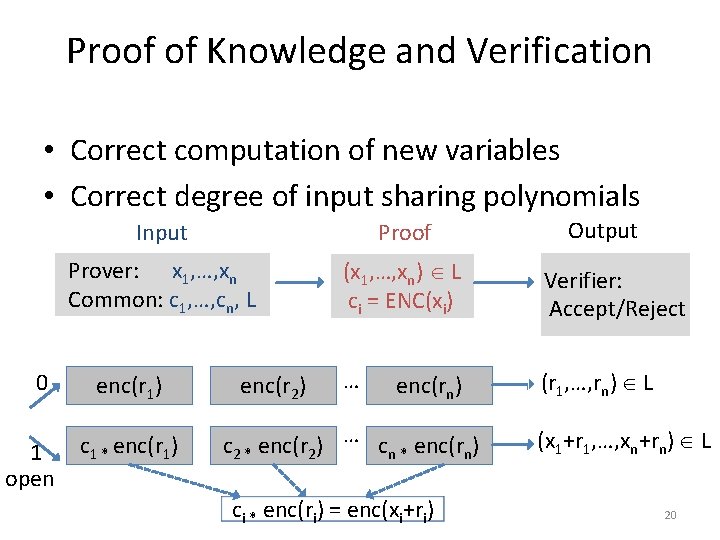
Proof of Knowledge and Verification • Correct computation of new variables • Correct degree of input sharing polynomials 0 1 open Output Input Proof Prover: x 1, …, xn Common: c 1, …, cn, L (x 1, …, xn) L ci = ENC(xi) Verifier: Accept/Reject … (r 1, …, rn) L enc(r 1) c 1 * enc(r 1) enc(r 2) enc(rn) c 2 * enc(r 2) … cn * enc(rn) ci * enc(ri) = enc(xi+ri) (x 1+r 1, …, xn+rn) L 20

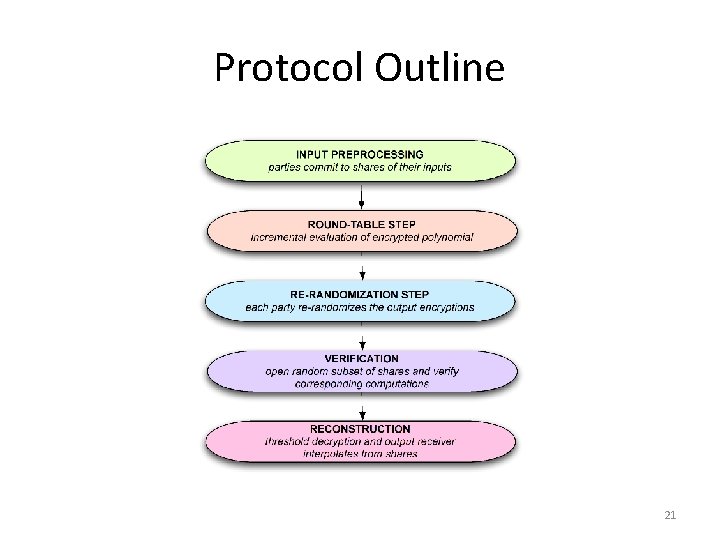
Protocol Outline 21

• Efficient preprocessing for each variable in the multivariate polynomial • Commit to shares of new variables 22

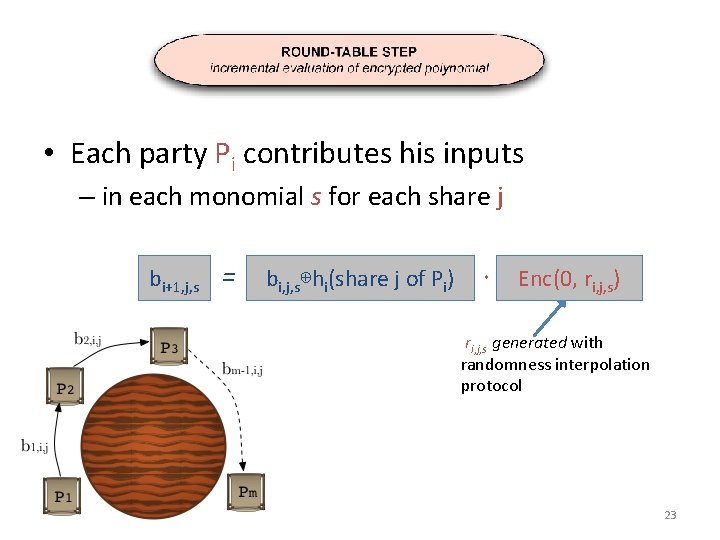
• Each party Pi contributes his inputs – in each monomial s for each share j bi+1, j, s = bi, j, s⊕hi(share j of Pi) · Enc(0, ri, j, s) ri, j, s generated with randomness interpolation protocol 23

• Each party re-randomizes the final output shares S 1, …, S 10 k. D – Randomizng polynomial Pj, 0(0) = 0 – Shares (1, Pj, 0(1)), . . . , (10 k. D, Pj, 0(10 k. D)) – Re-randomized output shares S’i = Si m · j=1 ENCpk(Pj, 0(i); rj, i) rj, k. D+2, . . . , rj, 10 k. D generated with randomness interpolation protocol 24

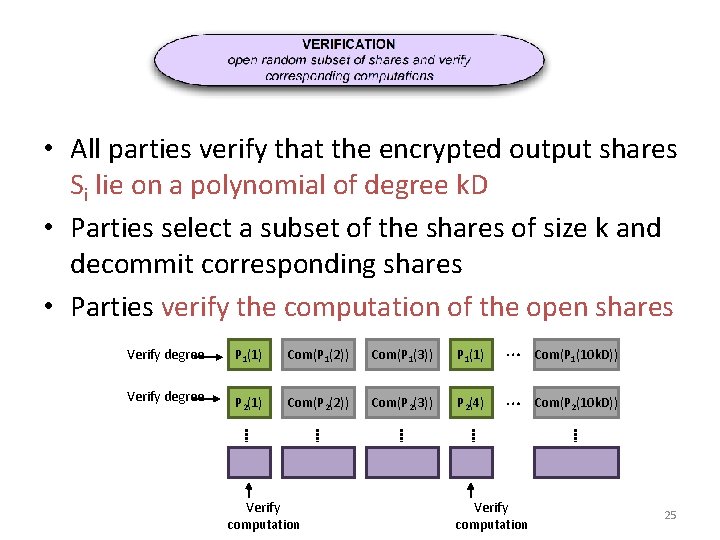
• All parties verify that the encrypted output shares Si lie on a polynomial of degree k. D • Parties select a subset of the shares of size k and decommit corresponding shares • Parties verify the computation of the open shares Verify degree P 1(1) Com(P 1(2)) Com(P 1(3)) P 1(1) … Com(P 1(10 k. D)) Verify degree P 2(1) Com(P 2(2)) Com(P 2(3)) P 2(4) … Com(P 2(10 k. D)) Verify computation 25

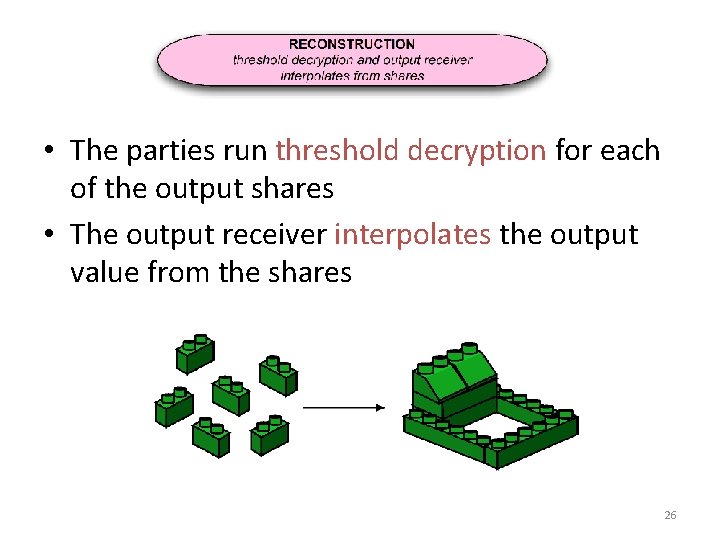
• The parties run threshold decryption for each of the output shares • The output receiver interpolates the output value from the shares 26

Protocol Complexities • Amortized – sharing with multiple secrets • Communication complexity – Round table – between consecutive parties: intermediate protocol messages • O(Dn(m-1)), m parties, n monomials, D sum of log variable degrees – Broadcast – input commitments, decommitments in verification phase • Smaller than polynomial representation m Lj • O(D ( j=1 log αj, t )) • αj, t highest degree of variable, Lj inputs for party j • Computational complexity • O(Dnm) 27

Multiparty set intersection P(x) = m-1 j=1 ri · Pi(x) + ri = ri, 1 + … + ri, m ri, j randomness from party j x Pi(x) represents the input set of party i • Optimizations: – Only two parties have inputs per each monomial – Inputs that are used only once do not need to be shared • Complexity - m parties, d inputs each: – Communication - O(md + 10 d log 2 d); CJS 10 – quadratic in number of parties, other solutions worse complexity – Computation - O(md 2 log d) 28

Thank You! • Questions? 29