14 Scattering 14 A Cross Section and Differential

14. Scattering 14 A. Cross Section and Differential Cross Section • Imagine many particles fired at and scattering from a small target • We want to predict the rate at which particles are scattered • It makes sense that it would be proportional to the number density n of the projectiles • It makes sense that it would be proportional to the speed |v| of the projectiles • Call the remaining proportionality constant • The cross-section has units of area • Classically, it is just the size of the target as viewed from the direction the projectiles are approaching • This formula is the definition of , and hence is correct by definition • | v| is the difference in speeds, even if everything is relativistic

Flux and Differential Cross-Section • The flux (in or out) is the number density times the relative velocity • Imagine we are far from a small target – It makes sense that scattered particles will be moving radially outwards • Imagine a spherical detector radius r covering all possible angles • The total rate for scattering will then be: • The cross-section is then: • If detector only covers some angles, restrict integral • Useful to define the differential cross-section:

Lab Frame and Center of Mass Frame There are two types of collision experiments v' that commonly occur: L v • The lab frame, where the target is stationary and the projectile collides with it v'cm • The center of mass frame, vcm where the incoming particles have net zero momentum • Usually easier to calculate in the cm frame • But then we must relate these two frames • Let the mass of the projectile be m and the target M • Commonly write things in terms of the ratio: • The velocity of the center of mass compared to the lab frame can be found:

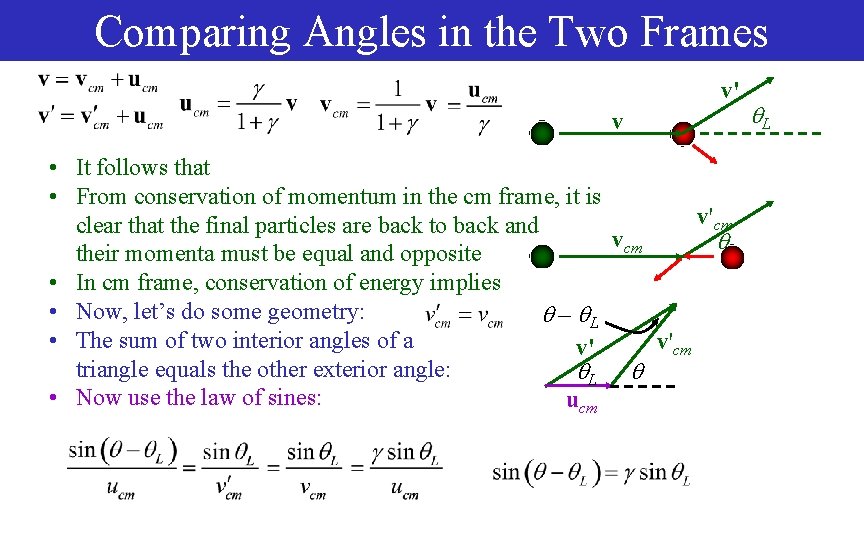
Choice of Axis and Description of Angles • Denote the velocities beforehand by v and vcm • Denote the velocities after by v' and v'cm • We will assume that the initial direction is in the z-direction v' v L v'cm • Then the scattering angles and L are the vcm polar angle of the direction of the outgoing particles in the two frames • The azimuthal angle and L will be the same • However, the polar angles and L will not be equal, because of the change in velocities between the two frames • The velocities in the two frames are related by the relative speed of the frames, ucm:

Comparing Angles in the Two Frames v' v • It follows that • From conservation of momentum in the cm frame, it is v'cm clear that the final particles are back to back and vcm their momenta must be equal and opposite • In cm frame, conservation of energy implies • Now, let’s do some geometry: – L • The sum of two interior angles of a v'cm v' triangle equals the other exterior angle: L • Now use the law of sines: ucm L

An Equivalent Formula • Algebra can make this into a more useful formula

Differential Cross-Section In the Two Frames • The cross-section and the differential cross-section can be computed in either the cm or the lab frame – But it is usually easier in the cm frame – We’ll do all calculations in the cm frame • Because the density n, the rate , and the relative velocity v are all the same in both frames, the total cross-section will be the same* • But because the angles are different, the differential cross-section will not be the same *True even relativistically

Quantum Mechanics and Cross-Section • We need to figure out how to calculate these expression in QM • Typically, we don’t want to use multiple particles at once • Fortunately, even for one particle, we have a pretty good idea of what the density and the flux are: – Number density corresponds to probability density: – Flux corresponds to probability current: • Our formula for differential cross section becomes: • Note that since j appears in numerator and denominator, no need to normalize

Solution in the Asymptotic Region • We now need to start solving Schrödinger’s Equation: • First define the asymptotic wave number k and the scaled potential U by • Schrödinger’s equation is now: • Assume potential vanishes (sufficiently quickly) at infinity – Roughly speaking, it must vanish faster than 1/r • For the incoming wave, we expect a plane wave in the +z direction • For the outgoing wave, makes sense to work in spherical coordinates • Since we are taking r , drop any terms with 1/r 2:

Asymptotic Form and Probability Currents • The gk corresponds to waves coming in from infinity – Physically wrong, so ignore it • The wave at infinity is therefore • We will need probability currents: • Probability current in: • Probability current out:

Cross Section from Asymptotic Form • Now we can do the differential cross-section: • And then we can get the total cross-section • Of course, we don’t yet have a clue what fk is

14 B. The Born Approximation The Basic Idea • We are trying to solve Schrodinger: • We know what in is, so write • Substitute in: • Now, imagine that we knew the right-hand side • We want to find a straightforward way to find if we know the right side • We will use superposition – Treat right hand side as a superposition of point sources • First step – replace right side by a point source at the origin and solve equation

The Green’s Function • Replace right side by a point source – To simplify, place it at the origin – Call the result the Green’s function G(r): • Spherically symmetric problem should have a spherically symmetric solution: • Write this out in spherical coordinates • Away from the origin, this is • This has solutions: • But we are looking for outgoing waves, not incoming, so • We still have to make sure it works at the origin – This will tell us what is

Getting G to Work at the Origin • It is hard to check this equation at the origin, because everything is infinite • To avoid this problem, integrate over a sphere of tiny radius R • Take the limit R 0: • We now know that • We could easily have put the source delta-function anywhere, so we generalize • Laplacian is understood to affect r, not r'

Solving the Actual Problem • We solved our equation for a “source” that is an arbitrary point • We now use this to solve the actual problem • Multiply top equation by U(r') • Integrate over r': • We therefore see that • Substitute back in to • We therefore have:

The Born Approximation • This looks useless – You can find if you know • Substitute this equation into itself repeatedly: • This is a perturbative expansion in U • If you keep just the first integral, it is called the first Born approximation, or sometimes, the Born approximation – We won’t go past the first Born approximation

Asymptotic Behavoir • We need behavior at large r to calculate cross-section • Define the change in wave number • Compare with the general asymptotic form: • We therefore have:

Differential and Total Cross-Section • We are now ready to get the cross section using • You then get the total cross section from • Often need to write K in Cartesian coordinates • Also handy to work out K 2:

Sample Problem Calculate the differential and total cross-section for scattering from the potential • Work on the Fourier transform of the potential • Since potential is spherically symmetric, we can pretend K is any direction – For convenience, pick it in the z-direction for this integration – Done thinking of K in z-direction • Now get the differential cross-section: • Recall that

Sample Problem (2) Calculate the differential and total cross-section for scattering from the potential • Now get the total cross-section

The Coulomb Potential • Consider the Coulomb potential, given by • We immediately get the differential cross section: • Rewrite in terms of the energy E = 2 k 2/2 Why this is a cheat: • We assumed potential falls off faster than 1/r, for = 0 it does not • Turns out this only causes a shift in the phase of at large r, so answer is right • Total cross-section is infinite • Comes from small angles • Experimentally, there is a minimum angle where we can tell if it scattered

14 C. Method of Partial Waves Spherically Symmetric Potentials • Suppose our potential is not small, but is spherically symmetric • We generally know how to find some solutions to Schrödinger’s equation: • The radial function then satisfies • Which we rewrite as: • Second order differential equation has two linearly independent solutions

Small r Behavior • For small r, the 1/r 2 term tends to dominate the U and k 2 terms • Two linearly independent solutions, that roughly go like: • The latter one is unacceptable, because we want finite • This means for each l, there is only one acceptable solution, up to normalization • We can always find these solutions, numerically if necessary – Assume we have done so • For large l, solution Rl tends to be very small near the origin – Roughly, it vanishes if kr << l • If U(r) vanishes or is negligible for r > r 0, you can ignore U(r) if l > kr 0

Large r Behavior • Assume the potential falls off quickly at large r – then ignore U(r) • Define x = kr, then • This equation has two known exact linearly independent solutions, called spherical Bessel functions: • Most general solution, at large r, is therefore a linear combination of these

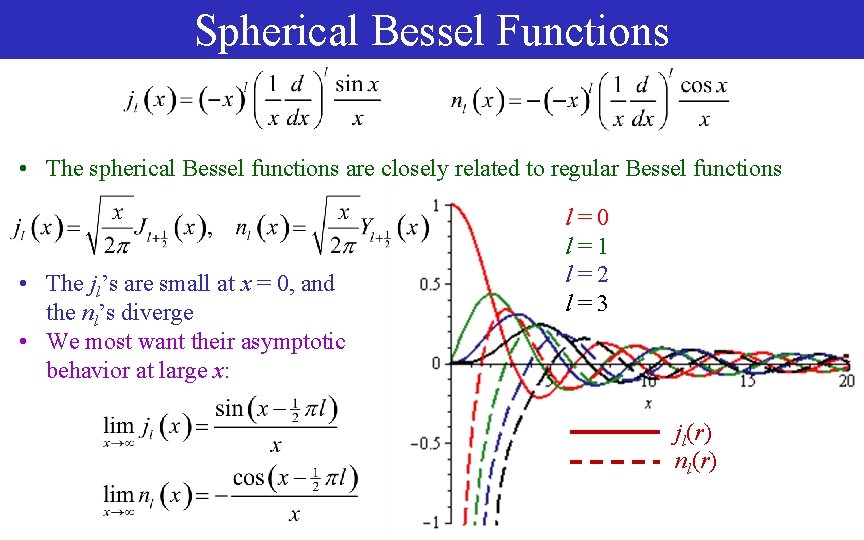
Spherical Bessel Functions • The spherical Bessel functions are closely related to regular Bessel functions • The jl’s are small at x = 0, and the nl’s diverge • We most want their asymptotic behavior at large x: l=0 l=1 l=2 l=3 jl(r) nl(r)

Asymptotic Solution • We assume we have the radial wave functions Rl, up to normalization • At large r, we know it takes the form • Write these constants in the form • The phase shift l is determined by the behavior of the Rl’s • The phase shift is what you need to finish this analysis – It vanishes for large l, because U(r) is irrelevant and nl badly behaved • The amplitude A is arbitrary • For large r, we now know what our solution looks like: • Use asymptotic form of spherical Bessel functions

Our Remaining Goal • Write this in terms of exponentials • This expression has waves coming in and going out in all directions • We want a wave that looks like • Most general solution will be a linear combination • Want to find a combination to make it look like what we want • First step: write eikz in terms of spherical harmonics at large r

ikz e in Spherical Harmonics at Large r • Since spherical harmonics are complete, everything can be written in terms of them, including eikz: • The functions clm can be found using orthogonality of the Ylm’s: • The Ylm’s go like eim , so the integral is easy: • Integrate by parts on cos repeatedly • We know these functions, so

Announcements ASSIGNMENTS Day Read Homework Today none 14. 3 Wednesday none Friday no class Test Thursday 1: 45, Olin 102 Covers through 13 Reviews on Monday and Wed. Homework Solutions Chapter 12 3/2

Putting it Together. . . • We have • We want • Where • We have to get the e-ikr terms to match, so try • Substitute this in: • Compare to eikz: • We therefore have:

The Differential and Total Cross-Section • Some algebra: • The differential cross section: • The total cross-section:

The Procedure • Find U(r): Now, for each value of l: – Find appropriate inner boundary conditions (typically Rl(0) = 0) – Solve numerically or analytically: – At large r, match your solution to: – Deduce phase shift: – Stop when l gets small, or l >> kr 0, where r 0 is where the potential gets small • Differential cross-section: • Total cross-section:

Sample Problem Calculate the differential and total crosssection from a hard sphere of radius a, with potential as given at right, where ka is small • • Perturbation theory cannot work, because the potential is infinite U(r) = V(r), because it is zero or infinity Boundary condition must be that Rl(a) = 0 We need to solve outside: • Solution of this is known: • Boundary condition: • Now we attempt to find phase shift:

Sample Problem (2) Calculate the differential and total crosssection from a hard sphere of radius a, with potential as given at right, where ka is small • • • Now use approximation ka small This means we need to keep up to l ~ ka <<1 Just keep l = 0 Look up spherical Bessel functions: Get the phase shift: Now find differential cross section: • We assumed ka small, so

Comments on Cross Sections • Interestingly, the cross-section is equal to the surface area (NOT the silhouette area) • Generally described as diffraction allows particles to scatter off of all sides • Note that whenever the scale of the potential is small, scattering is dominated by l = 1 (s-wave scattering) • All angles are scattered equally

Limits on Total Cross Sections • Note that if a particular value of l dominates the cross-section, then there is a limit on the cross section: • Before the discovery of the Higgs boson, it was pointed out that without the Higgs boson, the cross-section for WW scattering was predicted to be dominated by l = 0, and it grows as k 2 • Higgs boson cancels part of amplitude, and suppresses the cross section, once you get at or near the Higgs mass • Predicted Higgs, or something had to be lighter than 1000 Ge. V/c 2 – No lose theorem • Higgs discovered in 2012 at 126 Ge. V/c 2