11 5 Alternating series An alternating series has










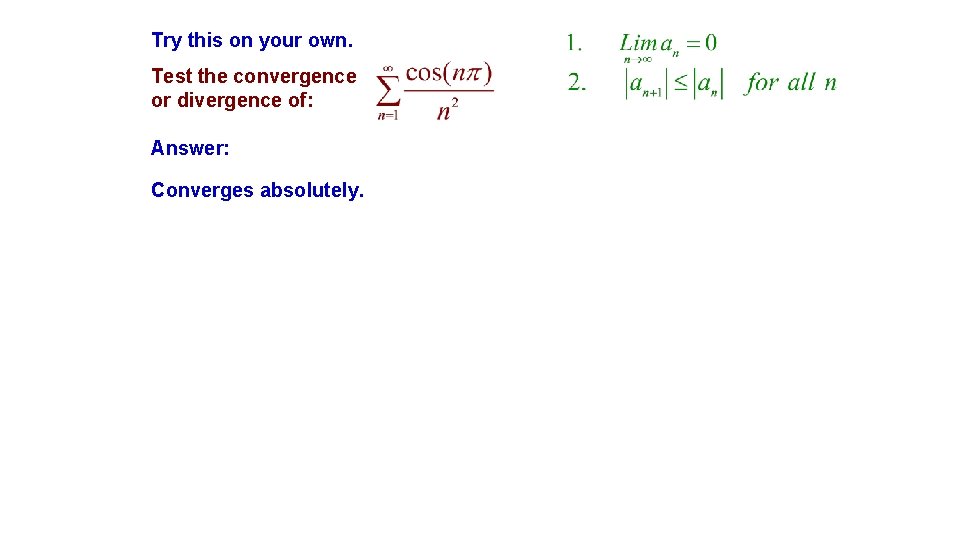




- Slides: 15

§ 11. 5 Alternating series An alternating series has its terms alternatively positive and negative. They can be represented in the following two forms. An alternating series will converge if the following two conditions are met. These conditions are valid only for an alternating series.

Conditional convergence and absolute convergence Consider the alternating series: It converges only under the conditions of an alternating series. Such convergence is called conditional convergence.

On the other hand, consider the alternating series: Both conditions are satisfied. Convergence occurs under conditions of alternative series as well as under general conditions of convergence. Such convergence is called absolute convergence.

Test the convergence or divergence of: Ignoring the sign, the nth term is:

Test the convergence or divergence of: Ignoring the sign, the nth term is: Both conditions for convergence of alternating series are met. It is conditional because compared to the diverging harmonic series

Test the convergence or divergence of: Ignoring the sign, the nth term is: Both conditions for convergence of alternating series are met. Can you check if this convergence is conditional or absolute. Hint: Compare it with the harmonic series.

Test the convergence or divergence of: Ignoring the sign, the nth term is: Both conditions for convergence of alternating series are met. Can you check if this convergence is conditional or absolute. Hint: Use integral test.

Test the convergence or divergence of: Ignoring the sign, the nth term is: Both conditions for convergence of alternating series are met.

Try this on your own. Test the convergence or divergence of: Answer: The series converges using conditions for alternating series

Test the convergence or divergence of: cos(n ) alternates between 1 and -1 for integer values of n
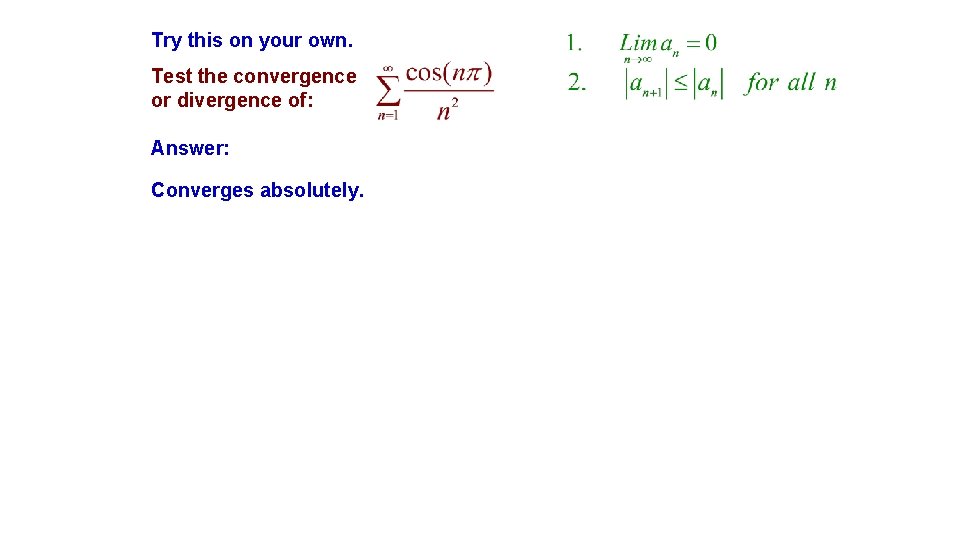
Try this on your own. Test the convergence or divergence of: Answer: Converges absolutely.

Test the convergence or divergence of: Ignoring the sign, the nth term is: Both conditions for convergence of alternating series are met. Can you check if this convergence is conditional or absolute. Hint: Compare it with the series:

Partial sum of n terms of an alternating series If the sum SN of n terms of an alternating series is used to approximate the sum S of the series, the error caused by the approximation will be RN = S – SN If a converging alternating series satisfies the condition an+1 an, then the absolute value of the remainder RN is less than or equal to the first neglected term. S – SN = RN an+1

Determine the number of terms required to approximate the sum of the convergent series with an error less than 0. 001 If n terms are used for the approximation, the error RN an+1 This can be solved only by trial and error. Use your calculator to evaluate for different values of n 0. 00026 < 0. 001 We should use 5 terms, n = 0 to n = 4 for this approximation.

Determine the number of terms required to approximate the sum of the convergent series with an error less than 0. 001 If n terms are used for the approximation, the error RN an+1 This can be solved only by trial and error. Use your calculator to evaluate for different values of n 0. 00098 < 0. 0001 We should use 3 terms, n = 1 to n = 3 for this approximation.
 Sum of alternating series
Sum of alternating series Alternating series test
Alternating series test Alternating series test
Alternating series test Lagrange error bound vs alternating series error bound
Lagrange error bound vs alternating series error bound Alternating series test
Alternating series test Alternating series graph
Alternating series graph Ratio test for absolute convergence
Ratio test for absolute convergence Alternating stress
Alternating stress If v1= vmsinwt, v2= vmsin( wt+45), then.......... *
If v1= vmsinwt, v2= vmsin( wt+45), then.......... * Cover uncover test vs alternating cover test
Cover uncover test vs alternating cover test Mary had a little lamb rhyme scheme
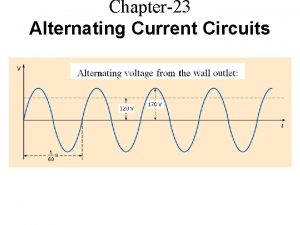
Mary had a little lamb rhyme scheme Alternating current ppt
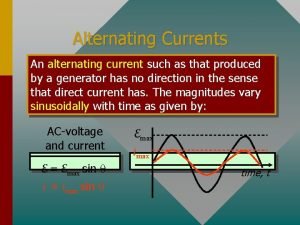
Alternating current ppt What is alternating emf
What is alternating emf Compare and contrast essay alternating example
Compare and contrast essay alternating example Alternating treatment design
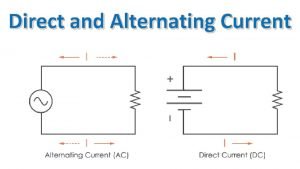
Alternating treatment design Direct current transformer
Direct current transformer