Lecture 15 Steady State Approximation Assuming that after

Lecture 15

Steady State Approximation • Assuming that after an initial induction period, the rates of change of concentrations of all reaction intermediates are negligibly small. • Substitute the above expression back to the rate law of B 0≈ [B] = (k 1/ k 2)[A] • Then • The integrated solution of the above equation is [C] ≈ (1 - )[A] 0

Example Derive the rate law for the decomposition of ozone in the reaction 2 O 3(g) → 3 O 2(g) on the basis of the following mechanism O 3 → O 2 + O k 1 O 2 + O → O 3 k 1’ O + O 3 → O 2 + O 2 k 2 Solution: First write the rate law for the reactant O 3 and the intermediate product O Applying the steady state approximation to [O] Plug the above relationship back to the rate law of [O 3]

Pre-equilibrium • Consider the reaction: A + B ↔ I → P when k 1’ >> k 2, the intermediate product, I, could reach an equilibrium with the reactants A and B. • Knowing that A, B, and I are in equilibrium, one gets: and • When expressing the rate of formation of the product P in terms of the reactants, we get

Example: Show that the pre-equilibrium mechanism in which 2 A ↔ I followed by I + B → P results in an overall third-order reaction. Solution: write the rate law for the product P Because I, and A are in pre-equilibrium so [I] = K [A]2 Therefore, the overall reaction order is 3.

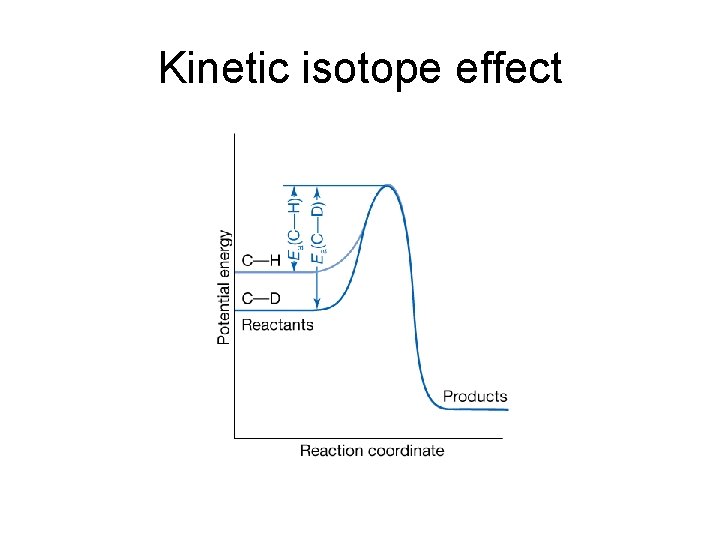
Kinetic isotope effect • Kinetic isotope effect: the decrease in the rate of a chemical reaction upon replacement of one atom in a reactant by a heavier isotope. • Primary kinetic isotope effect: the kinetic isotope effect observed when the rate-determining step requires the scission of a bond involving the isotope: with • Secondary kinetic isotope effect: the variation in reaction rate even though the bond involving the isotope is not broken to form product: with

Kinetic isotope effect

25. 8 Unimolecular reactions • The Lindemann-Hinshelwood mechanism A reactant molecule A becomes energetically excited by collision with another A molecule: A + A → A* + A The energized molecule may lose its excess energy by collision with another molecule: A + A* → A + A The excited molecule might shake itself apart to form products P A* → P The net rate of the formation of A* is

• If the reaction step, A + A → A* + A, is slow enough to be the rate determining step, one can apply the steady-state approximation to A*, so [A*] can be calculated as Then The rate law for the formation of P could be reformulated as Further simplification could be obtained if the deactivation of A* is must faster than A* P, i. e. , then in case

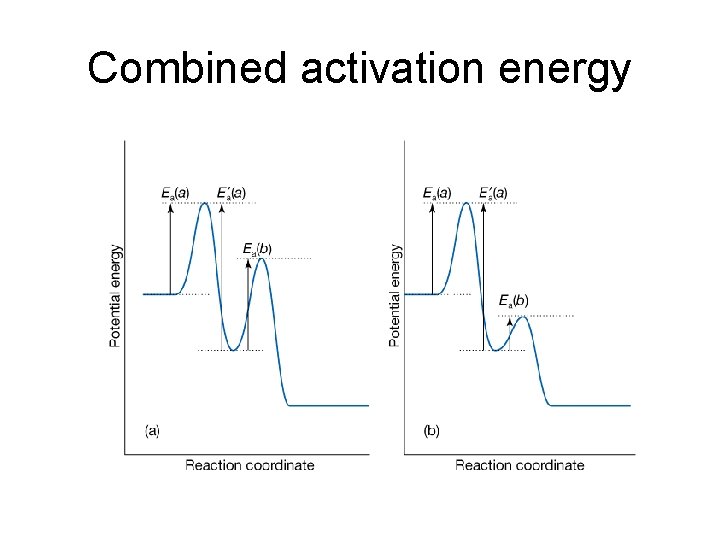
The activation energy of combined reactions • Consider that each of the rate constants the following reaction A + A → A* + A A + A* → A + A A* → P has an Arrhenius-like temperature dependence, one can get Thus the composite rate constant also has an Arrhenius-like form with activation energy, E = E 1 + E 2 – E 1’ Whether or not the composite rate constant will increase with temperature depends on the value of E, if E > 0, k will increase with the increase of temperature

Combined activation energy

Chapter 26: Kinetics of Complex reactions

26. 1 The rate laws of chain reactions • Consider thermal decomposition of acetaldehyde CH 3 CHO(g) → CH 4(g) + CO(g) v = k[CH 3 CHO]3/2 it indeed goes through the following steps: 1. Initiation: CH 3 CHO →. CH 3 +. CHO v = ki[CH 3 CHO] 2. Propagation: CH 3 CHO +. CH 3 → CH 4 + CH 3 CO. Propagation: CH 3 CO. →. CH 3 + CO 3. Termination: . CH 3 +. CH 3 → CH 3 • The net rates of change of the intermediates are: kp k’p kt

• Applying the steady state approximation: • Sum of the above two equations equals: • thus the steady state concentration of [. CH 3] is: • The rate of formation of CH 4 can now be expressed as the above result is in agreement with the three-halves order observed experimentally.

• Example: The hydrogen-bromine reaction has complicated rate law rather than the second order reaction as anticipated. H 2(g) + Br 2(g) → 2 HBr(g) Yield The following mechanism has been proposed to account for the above rate law. 1. Initiation: Br 2 + M → Br. + M ki 2. Propagation: Br. + H 2 → HBr + H. kp 1 H. + Br 2 → HBr + Br. kp 2 3. Retardation: H. + HBr → H 2 + Br. kr 4. Termination: Br. + M → Br 2 + M* kt derive the rate law based on the above mechanism.

• The net rates of formation of the two intermediates are • The steady-state concentrations of the above two intermediates can be obtained by solving the following two equations: • substitute the above results to the rate law of [HBr]

continued • The above results has the same form as the empirical rate law, and the two empirical rate constants can be identified as • Effects of HBr, H 2, and Br 2 on the reaction rate based on the equation