ERT 316 REACTION ENGINEERING CHAPTER 3 RATE LAWS

ERT 316: REACTION ENGINEERING CHAPTER 3 RATE LAWS & STOICHIOMETRY 1 Lecturer: Mrs Anis Atikah Ahmad Email: anisatikah@unimap. edu. my

OUTLINE PART 1: Rate Laws � Relative Rates of Reaction � Reaction Order & Rate Law � Reaction Rate Constant, k PART 2: Stoichiometry � Batch System Stoichiometric Table � Flow System Stoichiometric Table � Calculation for Concentration in terms of Conversion

1. RELATIVE RATES OF REACTION Reaction Stoichiometry EXAMPLE If NO 2 formed at 4 mol/m 3/s (r 3 NO 2= 4 mol/m /s), what is the rate of formation of NO?

1. RELATIVE RATES OF REACTION If NO 2 formed at 4 mol/m 3/s (r NO = 4 mol/m 3/s), 2 what is the rate of formation of NO?

1. RELATIVE RATES OF REACTION EXERCISE The Reaction: is carried out in a reactor. If at a particular point, the rate of disappearance of A is 10 mol/dm 3/s, what are the rates of B and C?

1. RELATIVE RATES OF REACTION The relative rates are Given, the rate of disappearance of A, -r. A, is 10 mol/dm 3/s r = -10 mol/dm A Thus, solving the rates of B & C;

2. REACTION ORDER & RATE LAW Rate law is a kinetic expression that gives the relationship between reaction rate, -r. A, and concentration. The reaction rate (rate of disappearance) depends on temperature and composition. It can be written as the product of reaction rate constant, k. A and a function of concentrations (activities) of the reactants involved in the reaction:

2. REACTION ORDER & RATE LAW Rate law is a kinetic expression that gives the relationship between reaction rate, -r. A, and concentration. For reaction in which the stoichiometric coefficient is 1 for ALL species: we shall delete the subscript on the specific reaction rate, (e. g. ; A in k. A) to let

2. 1 POWER LAW MODELS & ELEMENTARY RATE LAWS Power Law Model: The rxn is �� order wrt reactant A AND The rxn is �� order wrt reactant B The overall order of the reaction, n;

2. 1 POWER LAW MODELS & ELEMENTARY RATE LAWS The unit of the specific reaction, k, will vary with the order of reaction. Products Zero order (n=0) First order (n=1) Second order (n=2) Third order (n=3)

2. 1 POWER LAW MODELS & ELEMENTARY RATE LAWS Elementary reaction: a chemical reaction in which one or more of the chemical species react directly to form products in a single reaction step and with a single transition state. Products Unimolecular reaction Products Bimolecular reaction Elementary rate law: The rxn is said to follow the elementary rate law if the stoichiometic coefficients are IDENTICAL to the reaction order of each species.

EXAMPLES OF REACTION RATE LAWS

EXAMPLES OF REACTION RATE LAWS

EXAMPLES OF REACTION RATE LAWS

2. 2 NON-ELEMENTARY RATE LAWS Non-elementary rate laws: reactions that do not follow simple rate laws (power rate laws). Example 1: Homogeneous Rxn Gas phase synthesis of phosgene The kinetic rate law is: Rxn order: first order wrt to CO, three-halves order wrt Cl 2, five-halves order overall.

2. 2 NON-ELEMENTARY RATE LAWS Gas-solid catalyzed rxn: Hydrodemethylation of toluene (T) Example 2: Heterogeneous Rxn The rate of disappearance of toluene per mass of catalyst is : In terms of partial pressure rather than concentrations where KB & KT is the adsorption constants. follows Langmuir. Hinshelwood kinetics

2. 3 REVERSIBLE REACTIONS ⇌ For reversible rxn, all rate laws must reduce to thermodynamic relationship relating the reacting species concentrations at equilibrium. Thermodynamic Equilibrium Relationship

2. 3 REVERSIBLE REACTIONS EXAMPLE: combination rxn of 2 mol of benzene to form 1 mol H 2 and 1 mol diphenyl. k. B ⇌k -B symbolically; k. B ⇌k -B The rate of disappearance of benzene; OR The reverse rxn btween diphenyl & hydrogen; k-B ⇌ The rate of formation of benzene (in reverse direction);

2. 3 REVERSIBLE REACTIONS The net rate of formation of benzene is; Multiplying both sides by -1, we obtain the rate law of disappearance of benzene, -r. B

2. 3 REVERSIBLE REACTIONS Replacing the ratio of the reverse & forward rate law constant by equilibrium constants; where Concentration equilibrium constant

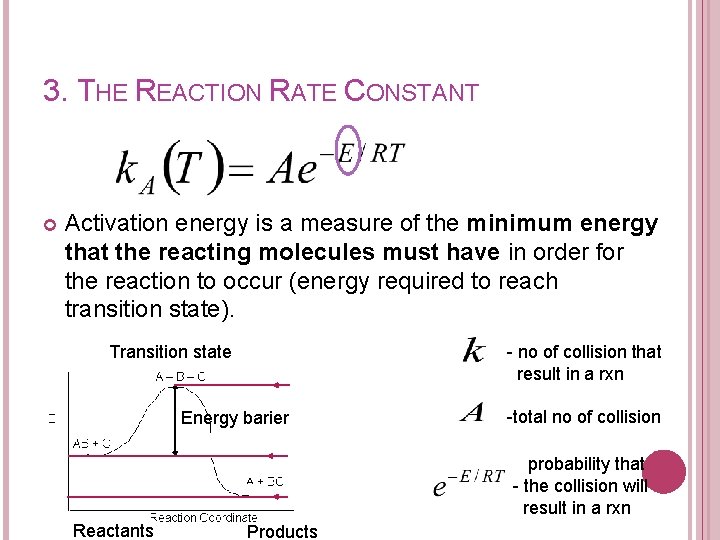
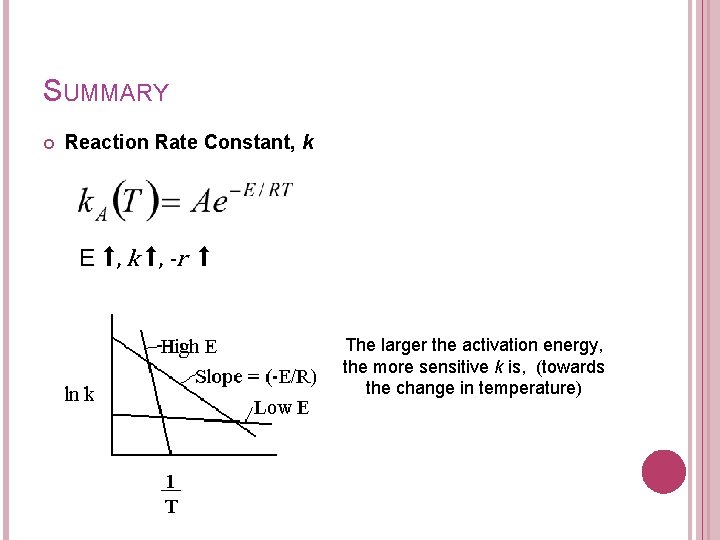
3. THE REACTION RATE CONSTANT Arrhenius equation A= preexponential factor or frequency factor E= activation energy, J/mol or cal/mol R=gas constant = 8. 314 J/mol-K = 1. 987 cal/mol-K T= absolute temperature, K -no of collision -probability that the collision will result in a reaction

3. THE REACTION RATE CONSTANT Activation energy is a measure of the minimum energy that the reacting molecules must have in order for the reaction to occur (energy required to reach transition state). Transition state - no of collision that result in a rxn Energy barier -total no of collision probability that - the collision will result in a rxn Reactants Products

3. THE REACTION RATE CONSTANT Taking a natural logarithm; E ⬆, k ⬆, -r = ⬆ The larger the activation energy, the more temperature sensitive k and thus the reaction rate.

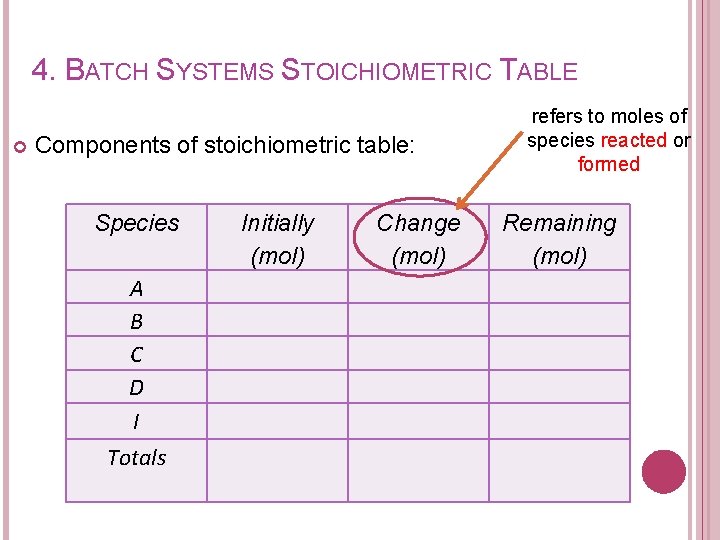
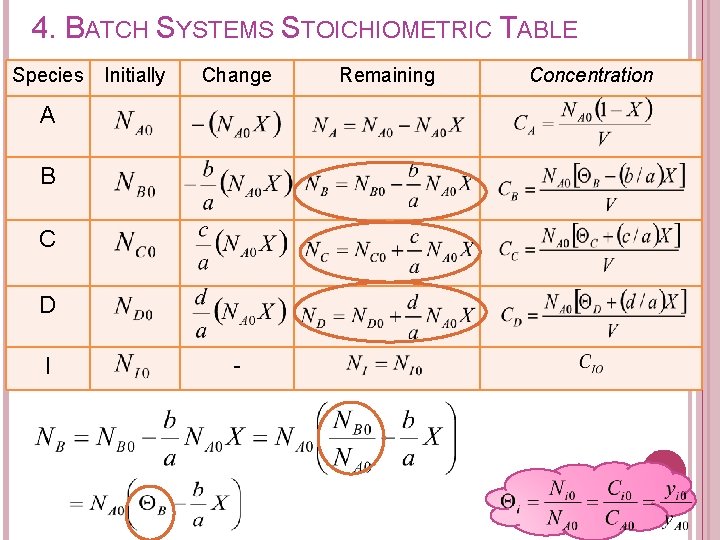
4. BATCH SYSTEMS STOICHIOMETRIC TABLE Purpose of developing stoichiometric table: � To determine the no of moles of each species remaining at a conversion of X.

4. BATCH SYSTEMS STOICHIOMETRIC TABLE Components of stoichiometric table: Species A B C D I Totals Initially (mol) Change (mol) refers to moles of species reacted or formed Remaining (mol)

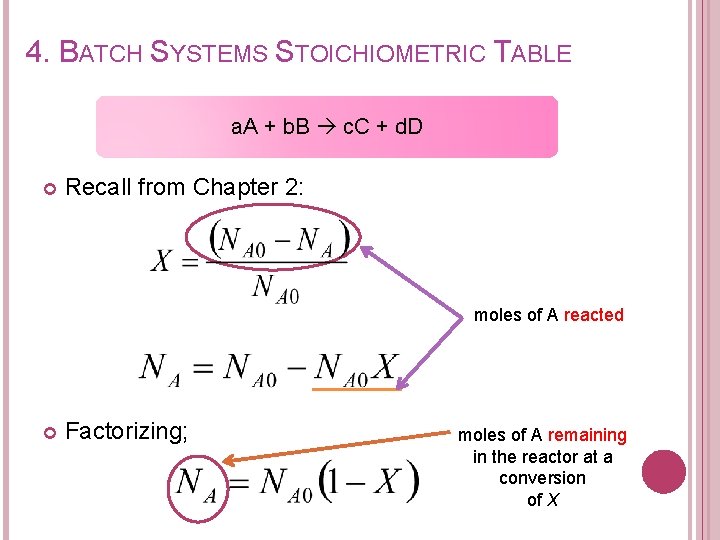
4. BATCH SYSTEMS STOICHIOMETRIC TABLE a. A + b. B c. C + d. D Recall from Chapter 2: moles of A reacted Factorizing; moles of A remaining in the reactor at a conversion of X

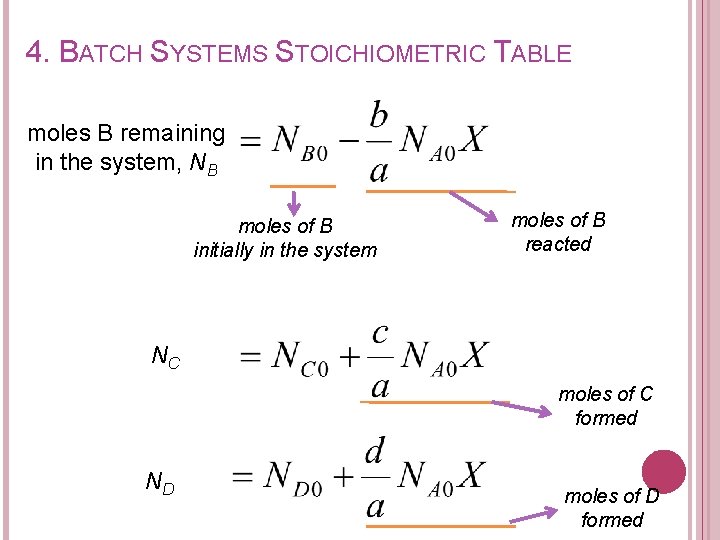
4. BATCH SYSTEMS STOICHIOMETRIC TABLE Moles B reacted, NB Moles C formed, NC Moles D formed, ND Moles B reacted Moles A reacted

4. BATCH SYSTEMS STOICHIOMETRIC TABLE moles B remaining in the system, NB moles of B initially in the system moles of B reacted NC moles of C formed ND moles of D formed

4. BATCH SYSTEMS STOICHIOMETRIC TABLE Species Initially (mol) Change (mol) A B C D I Totals - Remaining (mol)

4. BATCH SYSTEMS STOICHIOMETRIC TABLE Total no of moles per mole of A reacted can be calculated as: where Change in the total number of moles per mole of A reacted

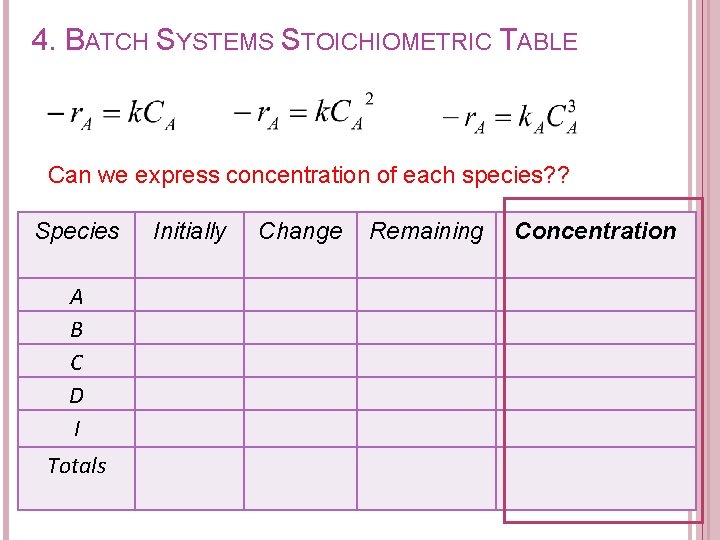
4. BATCH SYSTEMS STOICHIOMETRIC TABLE Can we express concentration of each species? ? Species A B C D I Totals Initially Change Remaining Concentration

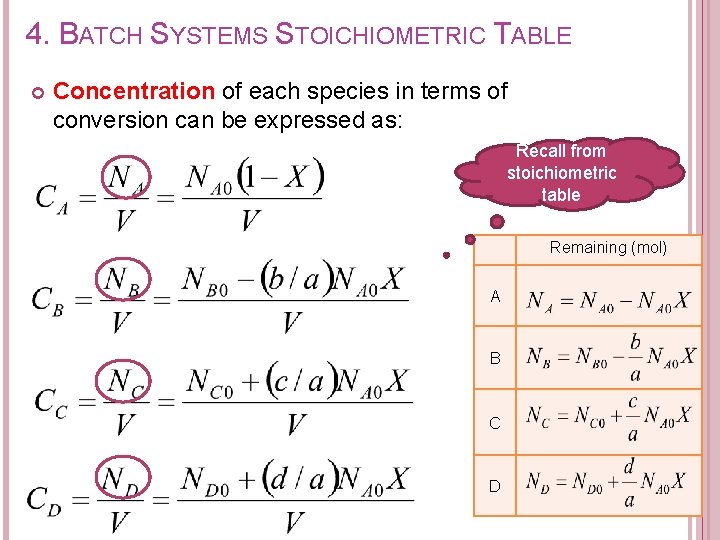
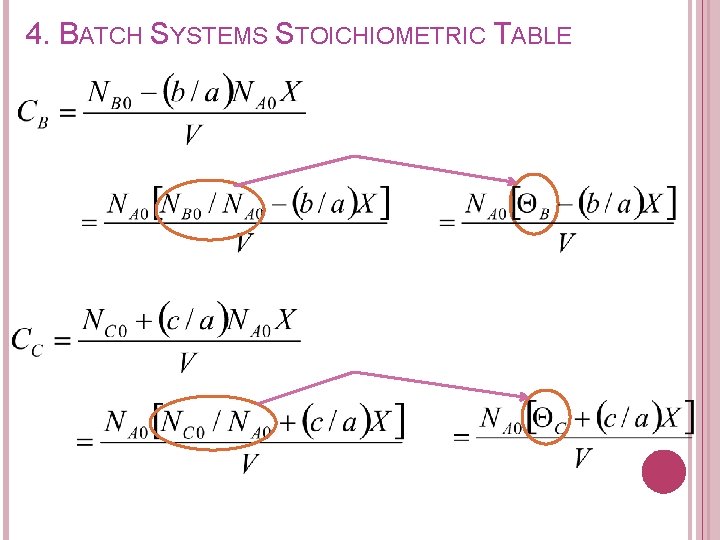
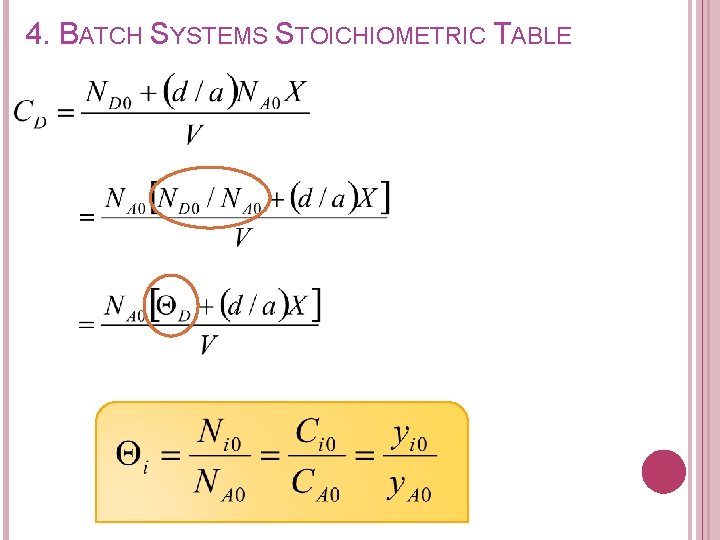
4. BATCH SYSTEMS STOICHIOMETRIC TABLE Concentration of each species in terms of conversion can be expressed as: Recall from stoichiometric table Remaining (mol) A B C D

4. BATCH SYSTEMS STOICHIOMETRIC TABLE

4. BATCH SYSTEMS STOICHIOMETRIC TABLE

4. BATCH SYSTEMS STOICHIOMETRIC TABLE Species Initially Change A B C D I - Remaining Concentration

4. BATCH SYSTEMS STOICHIOMETRIC TABLE Species Initially Change A B C D I - Remaining Concentration

4. BATCH SYSTEMS STOICHIOMETRIC TABLE EXAMPLE Given the saponification for the formation of soap from aqueous caustic soda & glyceryl stearate is: Letting X the conversion of sodium hydroxide, set up a stoichiometric table expressing the concentration of each species in terms of its initial concentration and the conversion.

4. BATCH SYSTEMS STOICHIOMETRIC TABLE EXAMPLE We know that this is a liquid-phase reaction. Therefore, V=V 0

4. BATCH SYSTEMS STOICHIOMETRIC TABLE EXAMPLE Species Initially Change A B C D I - Total 0 Remaining Concentration

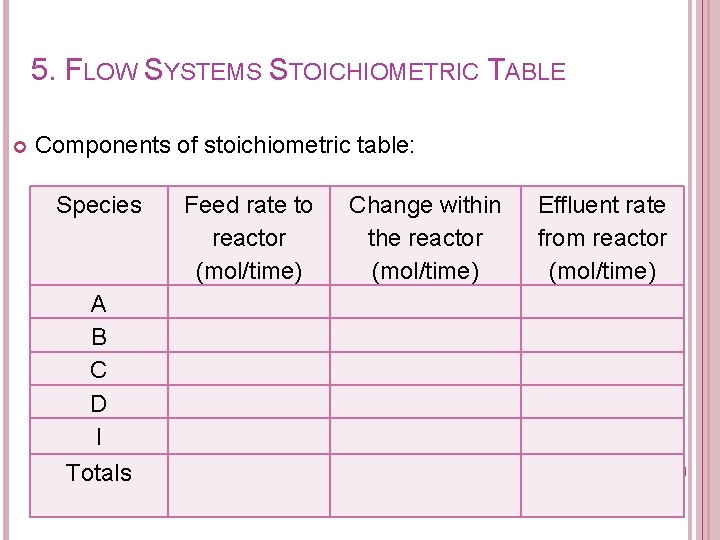
5. FLOW SYSTEMS STOICHIOMETRIC TABLE Purpose of developing stoichiometric table: � To determine the effluent flow rate of each species at a conversion of X.

5. FLOW SYSTEMS STOICHIOMETRIC TABLE Components of stoichiometric table: Species A B C D I Totals Feed rate to reactor (mol/time) Change within the reactor (mol/time) Effluent rate from reactor (mol/time)

5. FLOW SYSTEMS STOICHIOMETRIC TABLE Species Feed rate to reactor (mol/time) Change within the reactor (mol/time) A B C D I Totals - Effluent rate from reactor (mol/time) Concentration (mol/L)

QUIZ 3 Given a liquid phase reaction: A+ 2 B C + D The initial concentration of A and B are 1. 8 kmol/m 3 and 6. 6 kmol/m 3 respectively. Construct a stoichiometric table for a flow system considering A as the basis of calculation.

ANSWER FOR QUIZ 3 A+ 2 B C + D Given: Since C & D are products. From stoichiometry, we know that,

ANSWER FOR QUIZ 5 Species A B C D Totals Feed rate to reactor (mol/time) Change within the reactor (mol/time) Effluent rate from reactor (mol/time)

ANSWER FOR QUIZ 5 Substituting the numerical values; Species A B C D Totals Feed rate to reactor (mol/time) Change within the reactor (mol/time) Effluent rate from reactor (mol/time)

6. CONCENTRATION IN TERMS OF CONVERSION 1. For liquid phase: � Batch System:

6. CONCENTRATION IN TERMS OF CONVERSION 1. For liquid phase: � Flow System -

6. CONCENTRATION IN TERMS OF CONVERSION 2. For gas phase: � Batch System Need to substitute V from gas law equation From equation of state; At any time t, (1) At initial condition (t=0) (2) T= temperature, K P= total pressure, atm (1 atm= 101. 3 k. Pa) Z= compressibility factor R= gas constant = 0. 08206 dm 3 -atm/mol-K

6. CONCENTRATION IN TERMS OF CONVERSION 2. For gas phase: � Batch System (1) (2) Recall from stoichiometric table Dividing (1) by (2); (4) (3) Dividing (4) by NT 0 ;

6. CONCENTRATION IN TERMS OF CONVERSION 2. For gas phase: � Batch Applies for both batch and flow systems System Rearranging; Will be substitute in (3) At complete conversion (for irreversible rxn): X=1, NT=NTf

6. CONCENTRATION IN TERMS OF CONVERSION 2. For gas phase: � Batch System (3) Substituting the expression for NT/NT 0 in (3), If the compressibility factor are not change significantly during rxn, Z 0⩳Z (5)

6. CONCENTRATION IN TERMS OF CONVERSION 2. For gas phase: � Flow System Need to substitute υ from gas law equation From gas law, at any point in the reactor, (1) At the entrance of reactor; (2) Dividing (1) by (2) (3)

6. CONCENTRATION IN TERMS OF CONVERSION 2. For gas phase: � Flow System Recall from stoichiometric table Substituting for FT; (4)

6. CONCENTRATION IN TERMS OF CONVERSION 2. For gas phase: � Flow System Need to substitute υ from gas law equation (4) Substituting υ & F j; (5) Stoichiometric coefficient (d/a, c/a, -b/a, -a)

6. CONCENTRATION IN TERMS OF CONVERSION 2. For gas phase: a. A + b. B c. C + d. D System Concentration for each species: � Flow

SUMMARY Relative rate of reaction: Power Law Model:

SUMMARY Elementary rate law: The rxn that in which its stoichiometic coefficients are IDENTICAL to the reaction order of each species. Non-elementary rate laws: The reactions that do not follow simple rate laws (power rate laws) in which its stoichiometic coefficients are NOT IDENTICAL to the reaction order of each species. Reversible reaction: All rate laws must reduce to thermodynamic relationship relating the reacting species concentrations at equilibrium.

SUMMARY Reaction Rate Constant, k E ⬆, k ⬆, -r ⬆ The larger the activation energy, the more sensitive k is, (towards the change in temperature)

SUMMARY Stoichiometric Table for Batch Systems Species Initially Change A B C D I - Remaining

SUMMARY Stoichiometric Table for Flow Systems Species Feed rate to reactor (mol/time) Change within the reactor (mol/time) A B C D I Totals - Effluent rate from reactor (mol/time)

SUMMARY Expression of V and υ in calculating the concentration of each species: � � Batch systems Liquid phase: Gas phase: Flow systems Liquid phase: Gas phase:

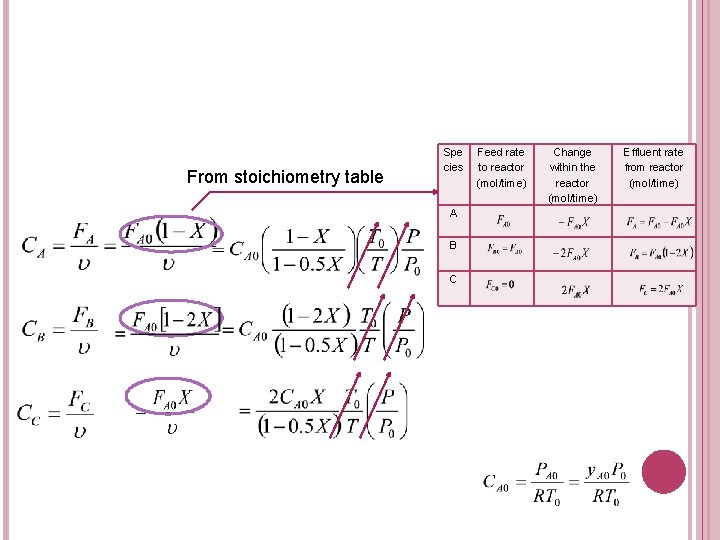
EXERCISE Given a gas phase reaction: A+ 2 B 2 C Construct a stoichiometric table for a flow system considering A as the basis of calculation with equimolar feed of 50% A and 50% B. Derive the concentration for each species (for an isothermal gas phase reaction, with no pressure drop). .

From stoichiometry table Spe cies A B C Feed rate to reactor (mol/time) Change within the reactor (mol/time) Effluent rate from reactor (mol/time)