Chapter 4 Interest Rates Term Structure Risks Paul

Chapter 4. Interest Rates - Term Structure Risks © Paul Koch 1 -1 A. Hedging interest rate exposure - more complicated than hedging exposure to the price of wheat. 1. Need entire term structure of interest rates to provide full description of level of interest rates. 2. Definition of term structure (or yield curve): The relation among interest rates on securities alike in every respect except term to maturity. a. For example, plot gov't securities with maturities from 1 month to 20 years. b. To hedge interest rate exposure, must decide: i. maturity of interest rate exposure, ii. maturity of hedge you require.

B. Types of Rates. © Paul Koch 1 -2 1. Treasury Rates – paid on debt issued by government. Assume governments won’t default (can print money). Taxes & Regulations mean Treasury issues have artificial demand. Treasury Rates are not truly “riskfree” - they are too low. 2. LIBOR – London Interbank Offer Rate that large international banks fund activities; Used as “riskfree rate. ” Rate that one int’l bank lends / borrows at with another (default risk ≈ 0). 3. Overnight Rate – Rate on overnight deposits between banks. Banks must maintain Required Reserves. One bank has excess Reserves; Second bank is short Reserves (has TBills). Second bank deposits TBills with First bank; receives cash (Reserves); Promises to repurchase TBills tomorrow future by returning cash (Reserves). Difference between cash received tomorrow & paid later is interest paid: Fed Funds Rate, Fed Funds Mkt, managed by Federal Reserve.

B. Types of Rates. © Paul Koch 1 -3 4. Repo Rate – rate on repurchase agreement. One institution needs short term cash (not nec. Reserves), another has it; First institution deposits Treasury Securities with other, receives cash; Promises to repurchase securities in near future. Difference between cash received now & paid later determines Repo Rate. (default risk ≈ 0): If first defaults, second keeps Treasury Securities; If second defaults, first keeps cash. Popular vehicle for short term borrowing / lending. 5. SWAP Rate – London Interbank Offer Rate that large international banks fund activities; Used as “riskfree rate. ” Repo Rate that one int’l bank lends / borrows at with another (risk ≈ 0). 6. Overnight Indexed SWAP Rate – OIS Rate on ON SWAP where fixed rate for a period (e. g. , 1 month) is exchanged for the Geometric Avg of the Overnight Rates (see 3. Fed Funds Rate, in US …). Allows ON borrowing/lending for a period to be swapped for a Fixed Rate.

B. Types of Rates. © Paul Koch 1 -4 7. Riskfree Rate – rate on riskfree asset (loan, investmt). Important! To value derivatives, want to set up riskfree portfolio – arb. Might use Treasury Bill Rate as riskfree rate. No; too low; in U. S. , Treasury Bills are given favorable treatment. Banks must hold them for reserves, Interest earned on Treasuries is not taxed at local level. Prior to the credit crisis of 2007, LIBOR Rates were used as riskfree rates. BUT in crisis, some banks got in trouble; LIBOR not considered riskfree. Since 2007, OIS Rate on SWAP is now used as “Riskfree Rate. ” (safer) Note: OIS Rate is a continually refreshed one-day Rate, for a SWAP where fixed rate for a period (e. g. , 1 month) is exchanged for the Geometric Avg of the Overnight Rates (see 3. Fed Funds Rate, in US …). Allows ON borrowing/lending for a period to be swapped for a Fixed Rate.

C. Measuring Interest Rates © Paul Koch 1 -5 Continuous Compounding & Discounting. 1. Amount A invested for n years at R per annum. a. compounded once/year, get A(1+R)n. b. compounded m times/year, get A(1+R/m)mn. c. Example: for n = 1 year, A = $100, R = 10%; m=1: get $100 x 1. 10 = $110. m=2: get $100 x 1. 052 = $110. 25 ($5 x. 10 x ½ year) m=4: get $100 x 1. 0254 = $110. 38 m : get Ae. Rn = $100 e. 10 = $110. 52 2. Continuous compounding, Ae. Rn ; e. Rn (1+R)n ; Continuous discounting, Ae-Rn ; e-Rn 1 / (1+R)n.

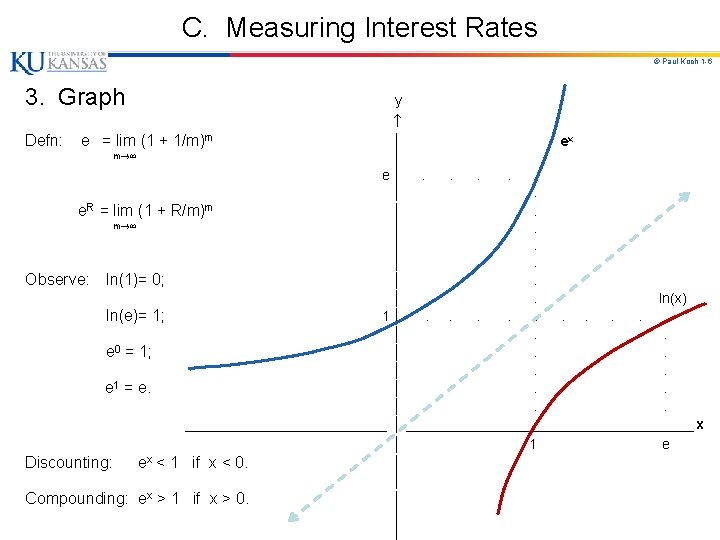
C. Measuring Interest Rates © Paul Koch 1 -6 3. Graph y Defn: e = lim (1 + 1/m)m │ ex m │ e │ . . . │ . R m e = lim (1 + R/m) │ . m │ . Observe: ln(1)= 0; │ . ln(x) ln(e)= 1; 1 │ . . . │ . e 0 = 1; │ . . e 1 = e. │ . . _____________ │ ___________________ x │ 1 e x Discounting: e < 1 if x < 0. │ │ x Compounding: e > 1 if x > 0. │ │ │

C. Measuring Interest Rates © Paul Koch 1 -7 4. Used to working with rates measured with annual, semiannual, or some other compounding frequency? Get used to continuous compounding / discounting! a. Can convert a continuously compounded rate to an equivalent rate compounded m times per annum: Let Rc = interest rate with continuous compounding; Rm = equivalent rate compounded m times p. a. Then Ae(Rc)n = A(1 + Rm / m)mn or e. Rc = (1 + Rm / m)m This means: Rc = m ln(1 + Rm / m) and Rm = m ( e Rc / m - 1) These equations convert a continuously compounded rate to an equivalent rate compounded m times p. a. , & vice versa.

D. Zero Rates (or Spot Rates) © Paul Koch 1 -8 1. n-year Zero Rate: interest rate on n-year investmt. a. Assume no intermediate payments; all principle & interest paid after n years. b. Also called “n-year zero coupon rate. ” 2. Zero Rates are determined by bootstrapping, using market prices on Treasury Securities with different maturities. Result is Zero-Coupon Yield Curve ; Could be Zero-Coupon Treasury Yield Curve, or Zero-LIBOR or OIS SWAP rate Yield Curves. See below and example in Hull.

E. Bond Pricing © Paul Koch 1 -9 1. Most bonds pay periodic coupons + face value at maturity. 2. Bond Price (PB = NPV of cash flows discounted at proper zero rates) Example: Face Value = F = $100; C / F = 6%; Coupon paid semi-annually, c = $3; Zero Rates: Maturity Zero rate % (discount rates) 0. 5 1. 0 1. 5 2. 0 5. 8 6. 4 6. 8 PB = 3 e -. 05 x 0. 5 + 3 e -. 058 x 1. 0 + 3 e -. 064 x 1. 5 + 103 e -. 068 x 2. 0 = $98. 39 3. Bond Yield: single discount rate that equates cash flows to mkt value. Same Example: Let mkt value = PB = $98. 39; Bond Yield (y) is solution to: $98. 39 = 3 e -y x 0. 5 + 3 e -y x 1. 0 + 3 e -y x 1. 5 + 103 e -y x 2. 0 ; Here, y = 6. 76%. Trades at Discount; PB < F if y > C/F (6. 76 > 6). [At Premium; PB > F if y < C/F. ] ($98. 39 < $100) (Bond yield)

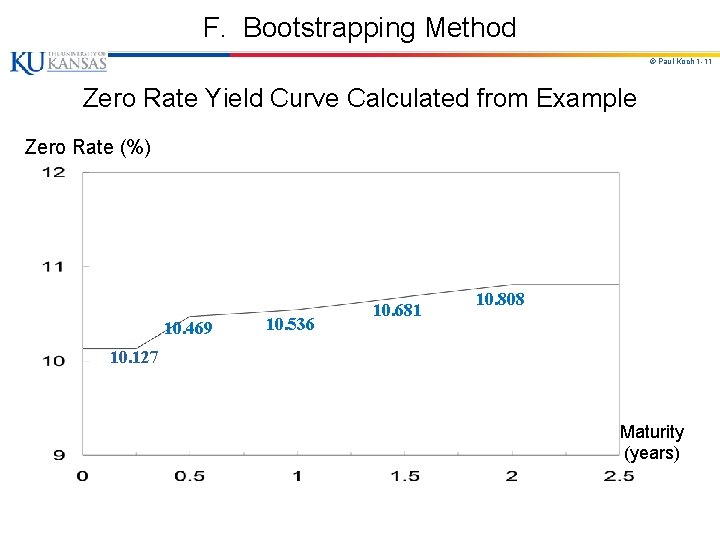
F. Bootstrapping Method to Determine Zero Rates © Paul Koch 1 -10 Sample Data: Bond Time to Maturity Annual Coupon Bond Price . $100 Market Price on $100 Treasury Securities $100 of different maturities $100 . 25 . 50 1. 00 1. 50 2. 00 $0 $0 $0 $8 (paid semiannually) $12 $97. 5 $94. 9 $90. 0 $96. 0 $101. 6 Principal Bond Price = 1. An amount $2. 5 can be earned on $97. 5 during 3 months. 2. The 3 -mo rate = Rm = 4 x ($2. 5 / $97. 5) = 10. 256% with qtrly compounding. 3. This is Rc = 10. 127% with continuous compounding. (See formula for Rc on page 1 -5. ) 4. Similarly, the 6 -month & 1 -year rates = Rc = 10. 469% & 10. 536%, with continuous compounding. 5. To calculate the 1. 5 -year rate, we solve the following : $96 = 4 e -. 10469 x 0. 5 + 4 e -. 10536 x 1. 0 + 104 e -Rc x 1. 5 to get Rc = 0. 10681 or 10. 681%. 6. Similarly the two-year rate is computed to be 10. 808%. Can now plot…

F. Bootstrapping Method © Paul Koch 1 -11 Zero Rate Yield Curve Calculated from Example Zero Rate (%) 10. 469 10. 536 10. 681 10. 808 10. 127 Maturity (years)

F. Bootstrapping Method © Kelly D. Welch 1 -12 7. Application to OIS Rates Can use similar bootstrap approach to determine: OIS Zero Rates -- the riskfree rates used to discount cash flows and value derivative securities. Recall: OIS Rate is a continually refreshed 1 -Day Rate on an Overnight SWAP, where fixed rate for a period (e. g. , 1 month) is exchanged for Geometric Avg of ON Rates (see 3. Fed Funds Rate, in US …). Allows ON borrowing / lending for a period to be swapped for a Fixed Rate.

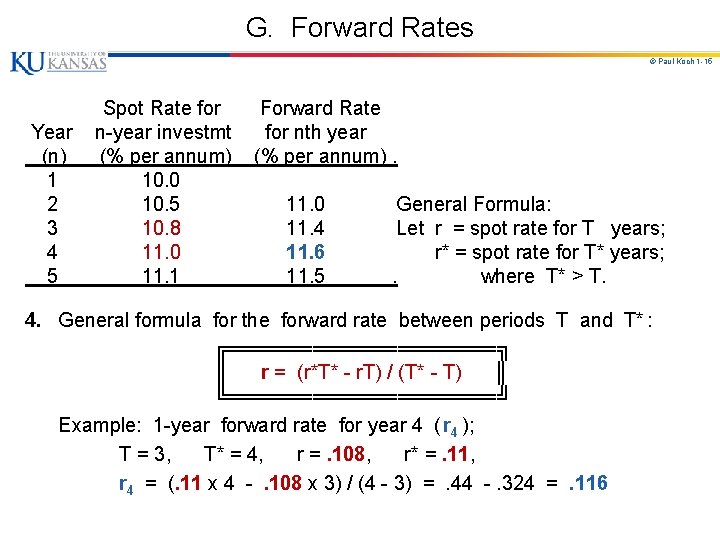
G. Forward Rates © Paul Koch 1 -13 Rates implied by current spot rates for periods in the future. 1. Calculation of Forward Rates. (Assume all rates are continuously compounded. ) Spot Rate for Forward Rate Year n-year investmt for nth year (n) (% per annum). 1 10. 0 -- 10. 0% for 1 yr $100 e. 10 = $110. 52 in 1 yr. 2 10. 5 11. 0 -- 10. 5% for 2 yr $100 e. 105 x 2 = $123. 37 in 2 yr. 3 10. 8 11. 4 4 11. 0 11. 6 Forward rate for year 2 is rate implied by spot rates 5 11. 1 11. 5 . for future period between end of yr 1 & end of yr 2. How do you get Forward rate for year 2 = 11. 0? a. Suppose you have $100 available for 2 years. Two choices: i. Can invest 2 years at 2 -yr spot rate (10. 5); Will earn 100 e. 105 x 2 = $123. 37 ii. Can invest 1 year at 1 -yr spot rate (10. 0), & reinvest yr 2 at future 1 -yr spot rate (r 1, 2 ); Will earn 100 e. 10 e r 1, 2 = 100 e(. 10 + r 1, 2) b. Problem: Today don't know future 1 -yr spot rate (r 1, 2). Forward rate for yr 2 (r 2) is future 1 -yr spot rate that would give same total result as i : 100 e (. 10 + r 2) = 100 e. 105 x 2 if (. 10 + r 2 ) = . 105 x 2 or r 2 = . 11 (Intuition: To get 10. 5% for 2 years, must get 11% the 2 nd year. )

G. Forward Rates © Paul Koch 1 -14 Spot Rate for Forward Rate Year n-year investmt for nth year (n) (% per annum). 1 10. 0 2 10. 5 11. 0 Forward rate for year 3 = r 3 3 10. 8 11. 4 is rate implied by spot rates 4 11. 0 11. 6 for future period between 5 11. 1 11. 5 . end of year 2 & end of year 3. How do you get r 3 ? Suppose you have $ available for 3 years. Two choices: i. Can invest for 3 years at 3 -yr spot rate (10. 8); Will earn 100 e. 108 x 3 ii. Can invest for 2 years at 2 -yr spot rate (10. 5), & reinvest for yr 3 at future 1 -yr spot rate (r 1, 3) ; Will earn 100 e. 105 x 2 e r 1, 3 = 100 e (. 105 x 2 + r 1, 3) Forward rate for yr 3 (r 3) is future 1 -yr spot rate that would give the same result as i. 100 e (. 105 x 2 + r 3) = 100 e. 108 x 3 if . 105 x 2 + r 3 = . 108 x 3 or r 3 = . 114 (To get 10. 8% for 3 years, must get 11. 4% 3 rd yr. ) [ . 21 + r 3 = . 324 ] [ =. 324 -. 21 ]

G. Forward Rates © Paul Koch 1 -15 Spot Rate for Forward Rate Year n-year investmt for nth year (n) (% per annum). 1 10. 0 2 10. 5 11. 0 General Formula: 3 10. 8 11. 4 Let r = spot rate for T years; 4 11. 0 11. 6 r* = spot rate for T* years; 5 11. 1 11. 5 . where T* > T. 4. General formula for the forward rate between periods T and T* : ╔══════════╗ ║ r = (r*T* - r. T) / (T* - T) ║ ╚══════════╝ Example: 1 -year forward rate for year 4 ( r 4 ); T = 3, T* = 4, r =. 108, r* =. 11, r 4 = (. 11 x 4 - . 108 x 3) / (4 - 3) = . 44 -. 324 = . 116

G. Forward Rates © Paul Koch 1 -16 5. Assuming you can borrow or invest at any spot rate, you can lock in forward rate for borrowing or lending in any future period. Calculation of Forward Rates . Spot Rate for Forward Rate Year n-year investmt for nth year (n) (% per annum). 1 10. 0 2 10. 5 11. 0 3 10. 8 11. 4 11. 0 11. 6 5 11. 1 11. 5 . Example: i. iii. iv. Borrow $100 @ 11% for 4 years; Invest this money at 10. 8% for 3 years; Result: inflow at end of yr 3 = 100 e. 108 x 3 = $138. 26 outflow at end of yr 4 = 100 e. 11 x 4 = $155. 27 Since 155. 27 = 138. 26 e. 116 , money is effectively being borrowed for the fourth year at 11. 6%.

H. The Zero-Coupon Yield Curve © Paul Koch 1 -17 1. Defn: Relation between yields on zero-coupon bonds and maturity. Forward curve Calculation of Forward Rates . yield Spot Rate for Forward Rate │ Zero-coupon curve Year n-year investmt for nth year │ (n) (% per annum). 11. 0 │ 1 10. 0 10. 5 │ 2 10. 5 11. 0 10. 0 │ 3 10. 8 11. 4 │ 4 11. 0 11. 6 │ Coupon-bearing bond curve 5 11. 1 11. 5 . │________________ maturity 2. Zero-Coupon Yield Curve versus Forward Rate Yield Curve. ** a. If zero-coupon yield curve is upward sloping, zero-coupon yield curve is below forward rate yield curve. 3. Zero-Coupon Yield Curve versus Yield Curve for Coupon-Bearing Bonds. ** a. If zero-coupon yield curve is upward sloping, zero-coupon yield curve is above yield curve for coupon-bearing bonds. Yield on coupon-bearing bonds is reduced by fact that investor gets some payments before maturity, when discount rates are lower than maturity rate. ** b. If yield curve is downward sloping, opposite.

I. Forward Rate Agreements (FRA’s) © Paul Koch 1 -18 1. OTC agreement that certain interest rate (RK) will apply to certain principal (L) during specified future period (T 1 to T 2). Can promise to lend / borrow with FRA. 2. Define: L = principal; RK = FRA interest earned over T 2 - T 1 (promised in FRA); RF = forward LIBOR over T 2 - T 1 (expected borrowing cost); R = actual LIBOR over T 2 - T 1 (actual borrowing cost). Hull calls this RM. 3. Cash Flows for holding FRA (promise to lend in future): T 1: T 2: +L ; borrow from bank later, at R (future actual rate); -L ; deposit (lend) according to FRA agreement. +L [ 1 + RK ( T 2 -T 1 ) ] earned in FRA agreement; -L [ 1 + R ( T 2 -T 1 ) ] paid to bank. Will eventually get to keep: L ( RK - R) ( T 2 - T 1 ). Problem: Today we don’t know future actual borrowing rate, R; But we do know forward LIBOR, RF; Assume this is expected borrowing rate. Thus, today’s expectation of what we will get to keep: L ( RK - RF ) ( T 2 - T 1 ). 4. Value of FRA today = L (RK - RF) (T 2 -T 1) e-R 2 T 2; where R 2 = T 2 - pd zero spot rate. This is NPV of expected future cash flows; Value of promise to lend over T 2 -T 1.

J. Theories of the Term Structure © Paul Koch 1 -19 1. Expectations Theory: Long term spot rates reflect unbiased expectations of future short term spot rates; i. e. , forward rates = expected future spot rates. Assumptions: i. Different maturities are perfect substitutes (investors don’t care - ST vs LT); ii. Money available for 2 years? – indifferent about investing 1 or 2 years … Implies: Shape of yield curve reveals expectations about whether rates will ↑ or ↓. i. If, market expects spot rates to remain stable (at today’s rates). forward rates = spot rates, & yield curve is flat. ii. If market expects spot rates to rise in future, 10. 5% for 2 years vs forward rates > spot rates, & yield curve slopes upward. 10% 1 st yr; 11% 2 nd yr. iii. If market expects spot rates to fall, forward rates < spot rates, & yield curve slopes downward. iv. If market expects rates to first rise then fall, yield curve may have “bump. "

J. Theories of the Term Structure © Paul Koch 1 -20 2. Liquidity Preference Theory: Investors prefer to invest short term, & will demand a premium for long positions. Borrowers prefer to borrow long term, & will pay a premium for long positions. Long term spot rates reflect expectations of future short term spot rates that are biased upward by a liquidity premium ; forward rates = expected future spot rates + liquidity premium. i. If market expects spot rates to remain stable, forward rates > spot rates by liquidity prem, & yield curve slightly upward sloping. ii. If market expects spot rates to rise, forward rates > spot rates by more than l. p. , & yield curve is steeper than (i). iii. If market expects spot rates to fall, forward rates may be <, =, or > spot rates, depending on size of liquidity premium and how much mkt expects rates to fall. (Flatter than i. , or slopes downward. ) iv. 'Normal' yield curve is upward sloping; Downward sloping yield curve is rare.