ECE 545Digital System Design with VHDL Lecture 1

ECE 545—Digital System Design with VHDL Lecture 1 Digital Logic Refresher Part A – Combinational Logic Building Blocks 1

Lecture Roadmap – Combinational Logic • Basic Logic Review • Basic Gates • De Morgan’s Law • Combinational Logic Building Blocks • • • Multiplexers Decoders, Demultiplexers Encoders, Priority Encoders Arithmetic circuits ROM. Implementing combinational logic using ROM. Tri-state buffers. 2

Textbook References • Combinational Logic Review • Stephen Brown and Zvonko Vranesic, Fundamentals of Digital Logic with VHDL Design, 2 nd or 3 rd Edition § Chapter 2 Introduction to Logic Circuits (2. 1 -2. 8 only) § Chapter 6 Combinational-Circuit Building Blocks (6. 16. 5 only) • OR your undergraduate digital logic textbook (chapters on combinational logic) 3

Basic Logic Review some slides modified from: S. Dandamudi, “Fundamentals of Computer Organization and Design” 4

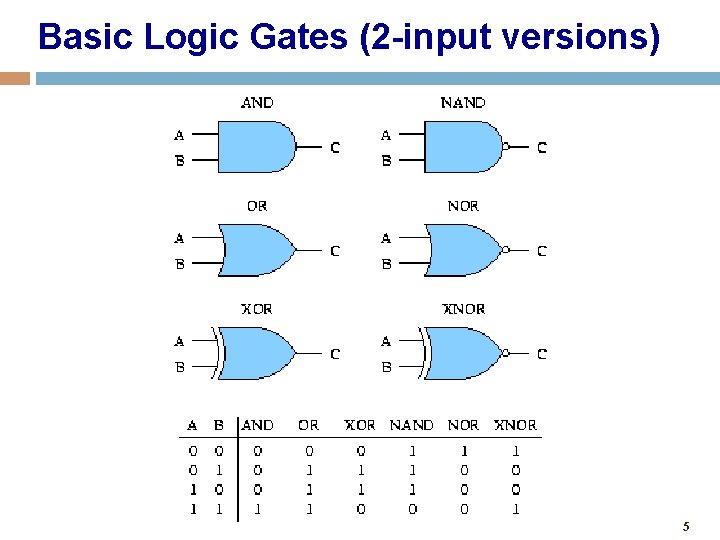
Basic Logic Gates (2 -input versions) 5

Basic Logic Gates Generalized • Simple logic gates • AND 0 if one or more inputs is 0 • OR 1 if one or more inputs is 1 • NAND = AND + NOT • 1 if one or more inputs is 0 • NOR = OR + NOT • 0 if one or more input is 1 • XOR 1 if an odd number of inputs is 1 • XNOR 1 if an even number of inputs is 1 • NAND and NOR gates require fewer transistors than AND and OR in standard CMOS • Functionality can be expressed by a truth table • A truth table lists output for each possible input combination 6

Number of Functions • Number of functions • With N logical variables, we can define N 2 2 functions • Some of them are useful • AND, NOR, XOR, … • Some are not useful: • Output is always 1 • Output is always 0 • “Number of functions” definition is useful in proving completeness property 7

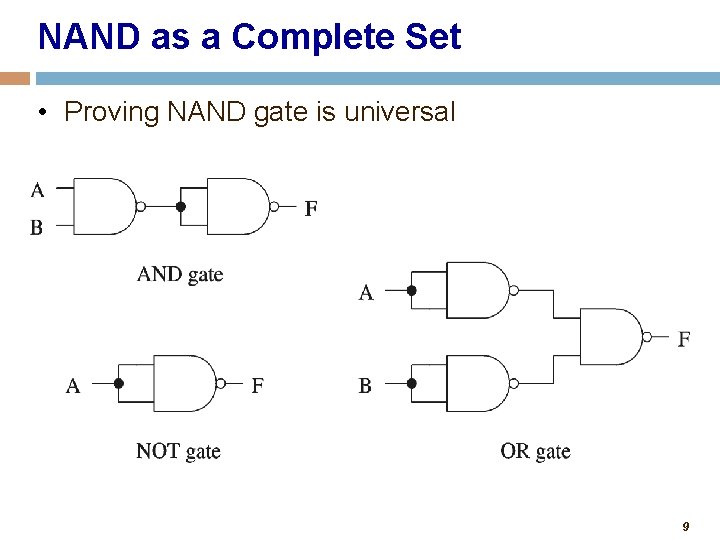
Complete Set of Gates • Complete sets • A set of gates is complete • if we can implement any logic function using only the type of gates in the set • Some example complete sets • {AND, OR, NOT} complete set • {AND, NOT} • {OR, NOT} • {NAND} • {NOR} Not a minimal • Minimal complete set • A complete set with no redundant elements. 8

NAND as a Complete Set • Proving NAND gate is universal 9

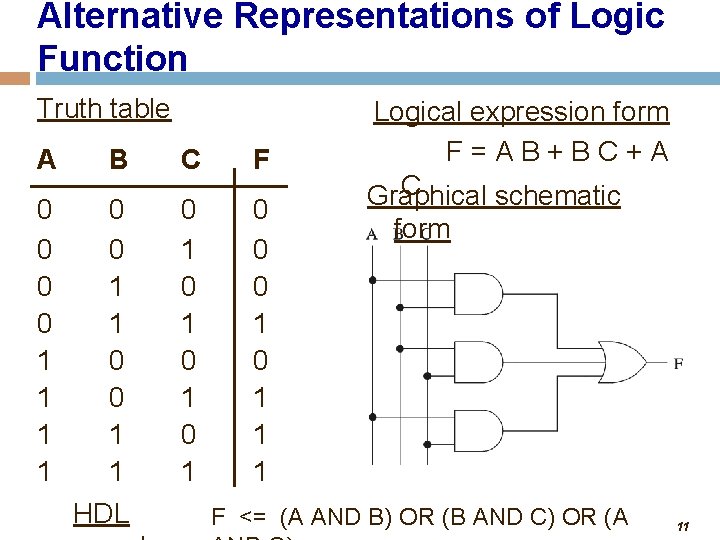
Logic Functions • Logic functions can be expressed in several ways: • • Truth table Logical expressions Graphical schematic form HDL code • Example: • Majority function • Output is one whenever majority of inputs is 1 • We use 3 -input majority function 10

Alternative Representations of Logic Function Truth table A B C F 0 0 1 1 HDL 0 1 0 1 0 0 0 1 1 1 Logical expression form F=AB+BC+A C Graphical schematic form F <= (A AND B) OR (B AND C) OR (A 11

Boolean Algebra Boolean identities AND version OR Name version Identity x. 1 = x x+0=x Complement x. x’ = 0 x + x’ = 1 Commutative x. y = y. x x+y=y+x Distribution x. (y+z) = xy+xz x+ (y. z) = (x+y) (x+z) Idempotent x. x = x x+x=x 12

Boolean Algebra (cont’d) • Boolean identities (cont’d) Name AND version OR version Involution Absorption (x. y) = x Associative (y + z) = de Morgan x = (x’)’ x. (x+y) = x x. (y. z) = (x. y). z --x+ x+ (x + y) + z (x. y)’ = x’ + y’ (x + y)’ = 13

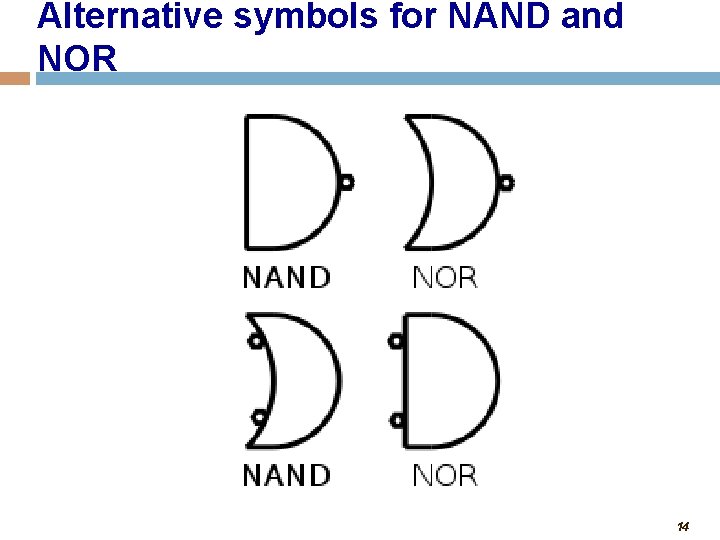
Alternative symbols for NAND and NOR 14

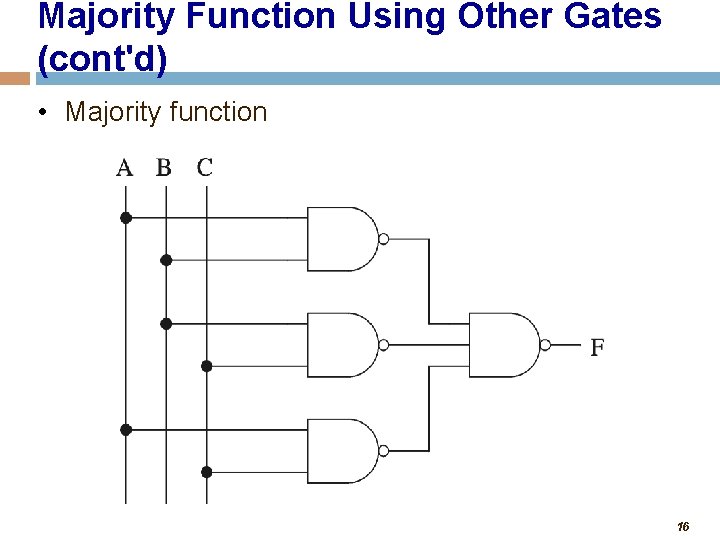
Majority Function Using Other Gates • Using NAND gates • Get an equivalent expression A B + C D = (A B + C D)’’ • Using de Morgan’s law A B + C D = ( (A B)’. (C D)’)’ • Can be generalized • Example: Majority function A B + B C + AC = ((A B)’. (B C)’. (AC)’)’ 15

Majority Function Using Other Gates (cont'd) • Majority function 16

Combinational Logic Building Blocks Some slides modified from: S. Dandamudi, “Fundamentals of Computer Organization and Design” S. Brown and Z. Vranesic, "Fundamentals of Digital Logic" 17

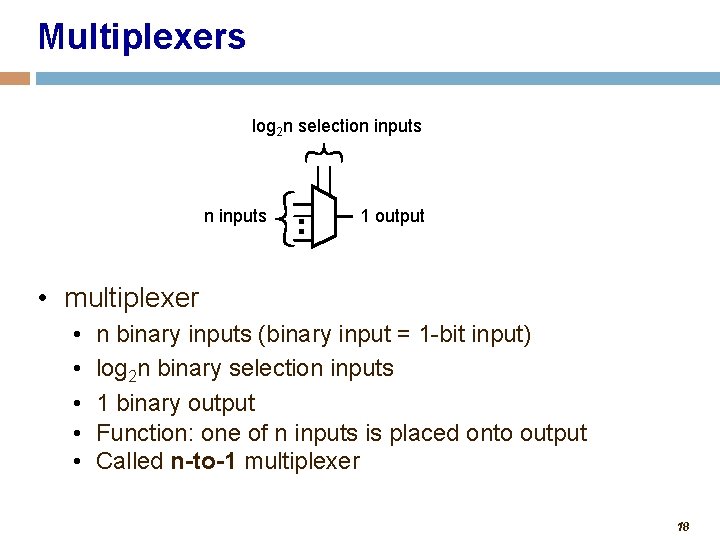
Multiplexers log 2 n selection inputs 1 output • multiplexer • • • n binary inputs (binary input = 1 -bit input) log 2 n binary selection inputs 1 binary output Function: one of n inputs is placed onto output Called n-to-1 multiplexer 18

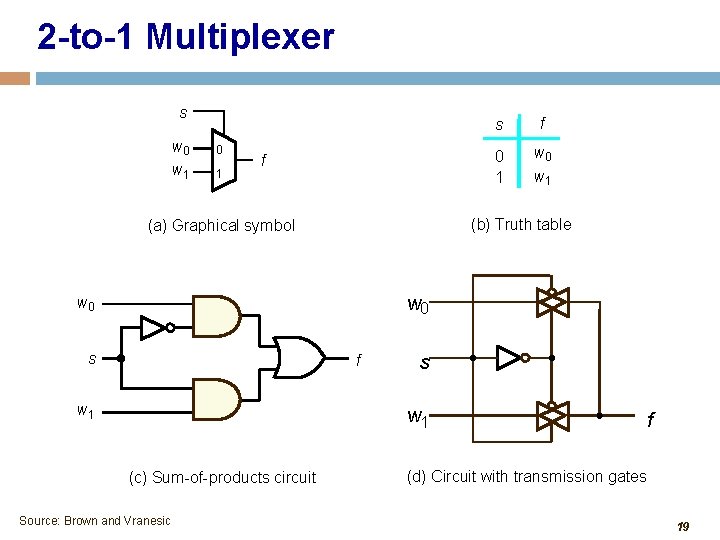
2 -to-1 Multiplexer s w 0 w 1 0 1 f s f 0 1 w 0 w 1 (b) Truth table (a) Graphical symbol w 0 s f w 1 s w 1 (c) Sum-of-products circuit Source: Brown and Vranesic f (d) Circuit with transmission gates 19

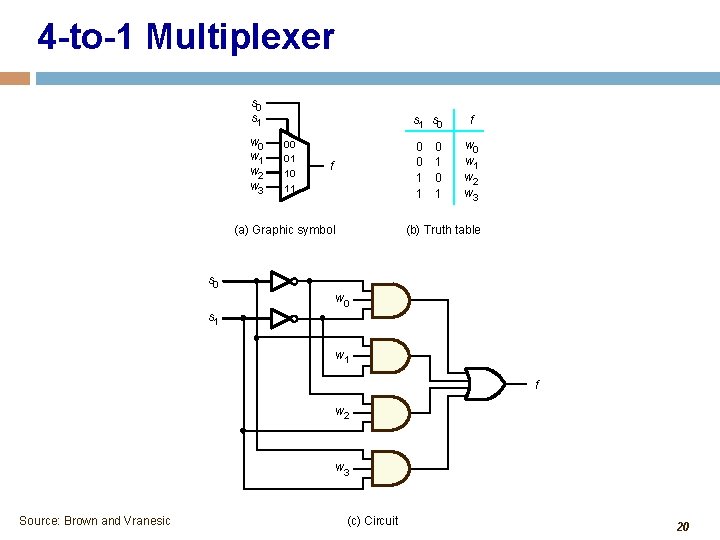
4 -to-1 Multiplexer s 0 s 1 w 0 w 1 w 2 w 3 s 1 s 0 00 01 10 11 0 0 1 1 f (a) Graphic symbol 0 1 f w 0 w 1 w 2 w 3 (b) Truth table s 0 w 0 s 1 w 1 f w 2 w 3 Source: Brown and Vranesic (c) Circuit 20

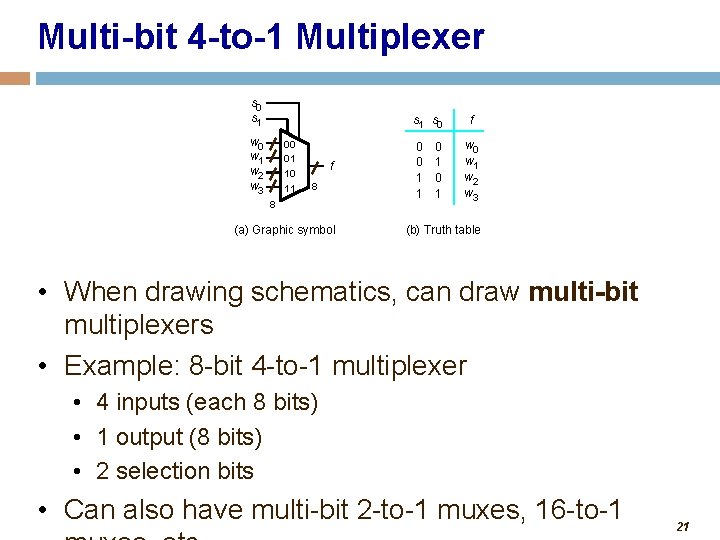
Multi-bit 4 -to-1 Multiplexer s 0 s 1 s 0 w 1 w 2 w 3 00 01 10 11 f 8 8 (a) Graphic symbol 0 0 1 1 0 1 f w 0 w 1 w 2 w 3 (b) Truth table • When drawing schematics, can draw multi-bit multiplexers • Example: 8 -bit 4 -to-1 multiplexer • 4 inputs (each 8 bits) • 1 output (8 bits) • 2 selection bits • Can also have multi-bit 2 -to-1 muxes, 16 -to-1 21

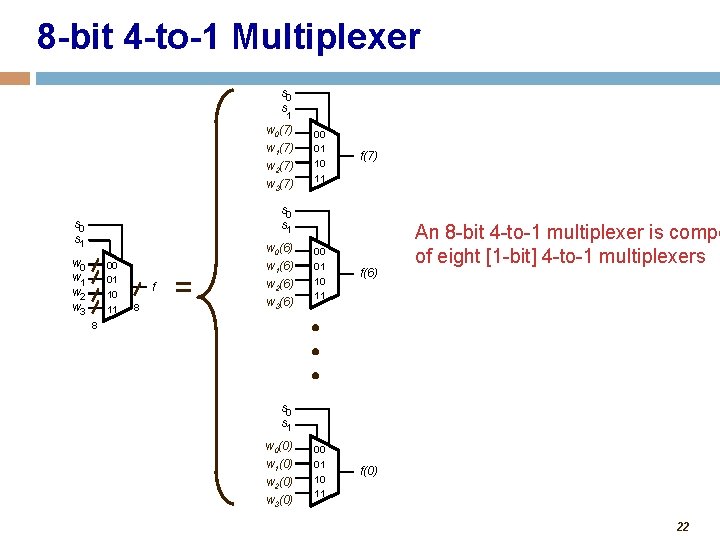
8 -bit 4 -to-1 Multiplexer s 0 s 1 w 0(7) w 1(7) w 2(7) w 3(7) 00 01 10 11 f(7) s 0 s 1 w 0 w 1 w 2 w 3 00 01 10 11 f 8 = w 0(6) w 1(6) w 2(6) w 3(6) 00 01 10 11 f(0) An 8 -bit 4 -to-1 multiplexer is compo of eight [1 -bit] 4 -to-1 multiplexers 8 s 0 s 1 w 0(0) w 1(0) w 2(0) w 3(0) 22

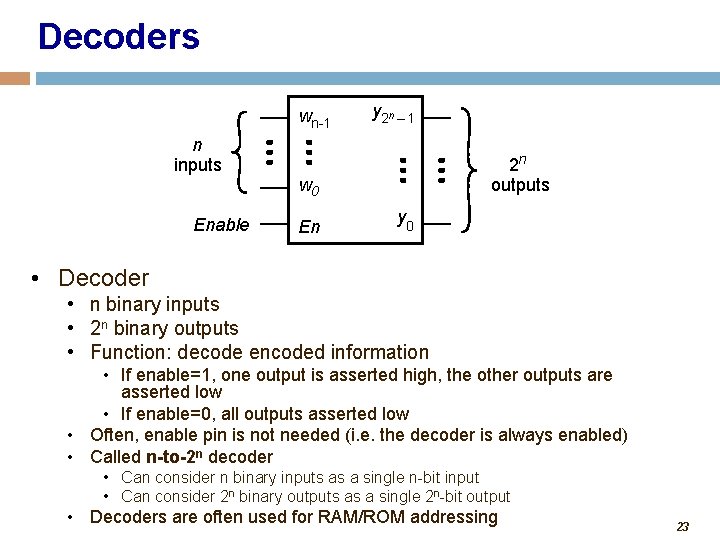
Decoders wn-1 n inputs Enable y 2 n – 1 2 n outputs w 0 En y 0 • Decoder • n binary inputs • 2 n binary outputs • Function: decode encoded information • If enable=1, one output is asserted high, the other outputs are asserted low • If enable=0, all outputs asserted low • Often, enable pin is not needed (i. e. the decoder is always enabled) • Called n-to-2 n decoder • Can consider n binary inputs as a single n-bit input • Can consider 2 n binary outputs as a single 2 n-bit output • Decoders are often used for RAM/ROM addressing 23

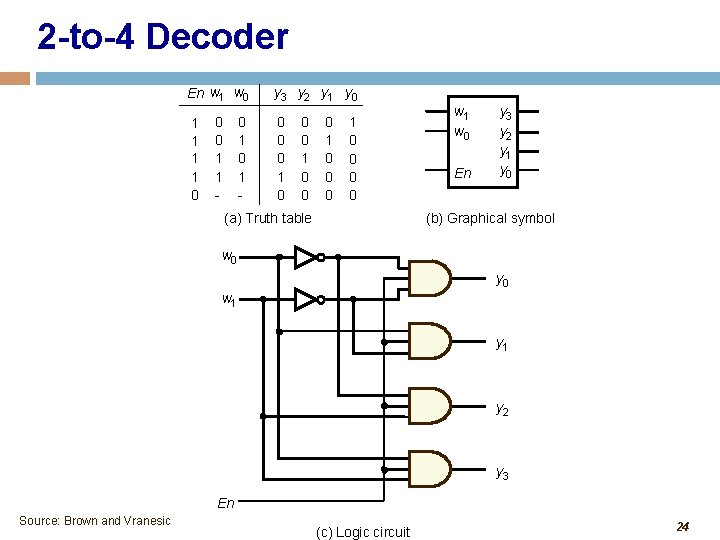
2 -to-4 Decoder En w 1 w 0 1 1 0 0 0 1 1 - 0 1 - y 3 y 2 y 1 y 0 0 1 0 0 0 0 (a) Truth table w 1 w 0 En y 3 y 2 y 1 y 0 (b) Graphical symbol w 0 y 0 w 1 y 2 y 3 En Source: Brown and Vranesic (c) Logic circuit 24

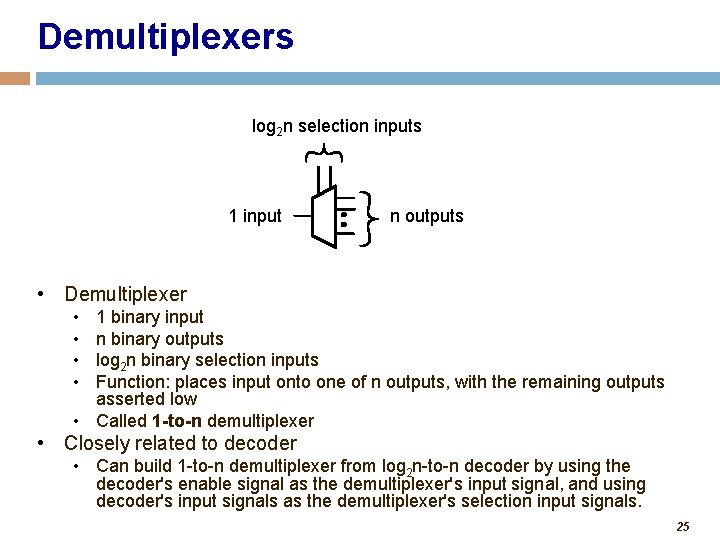
Demultiplexers log 2 n selection inputs 1 input n outputs • Demultiplexer • • 1 binary input n binary outputs log 2 n binary selection inputs Function: places input onto one of n outputs, with the remaining outputs asserted low • Called 1 -to-n demultiplexer • Closely related to decoder • Can build 1 -to-n demultiplexer from log 2 n-to-n decoder by using the decoder's enable signal as the demultiplexer's input signal, and using decoder's input signals as the demultiplexer's selection input signals. 25

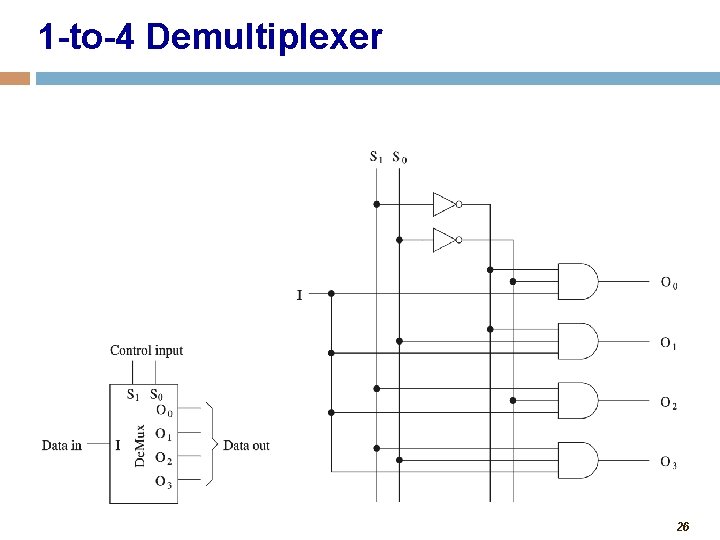
1 -to-4 Demultiplexer 26

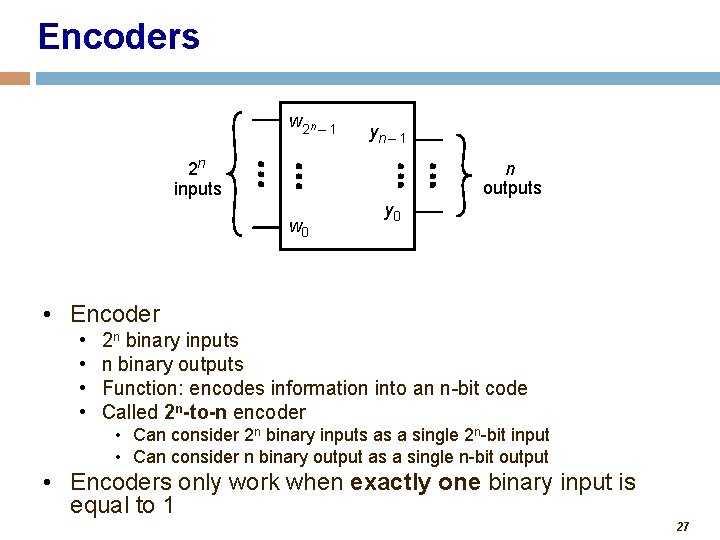
Encoders w 2 n – 1 yn – 1 2 n inputs n outputs w 0 y 0 • Encoder • • 2 n binary inputs n binary outputs Function: encodes information into an n-bit code Called 2 n-to-n encoder • Can consider 2 n binary inputs as a single 2 n-bit input • Can consider n binary output as a single n-bit output • Encoders only work when exactly one binary input is equal to 1 27

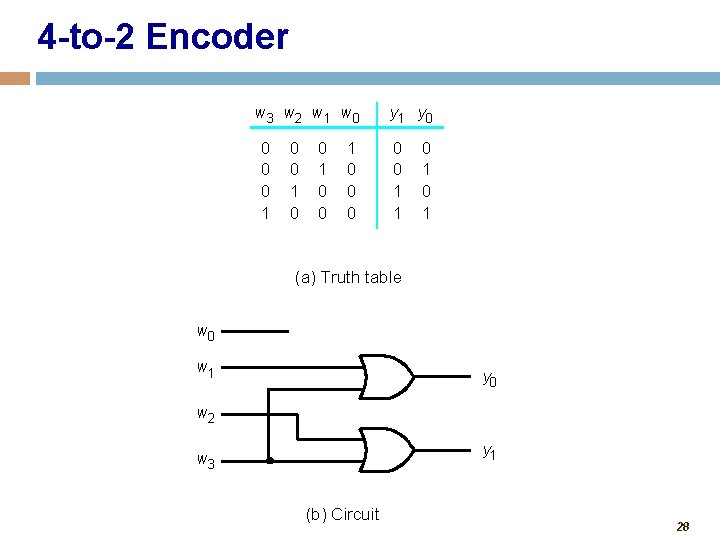
4 -to-2 Encoder w 3 w 2 w 1 w 0 0 1 0 0 0 y 1 y 0 0 0 1 1 0 1 (a) Truth table w 0 w 1 y 0 w 2 y 1 w 3 (b) Circuit 28

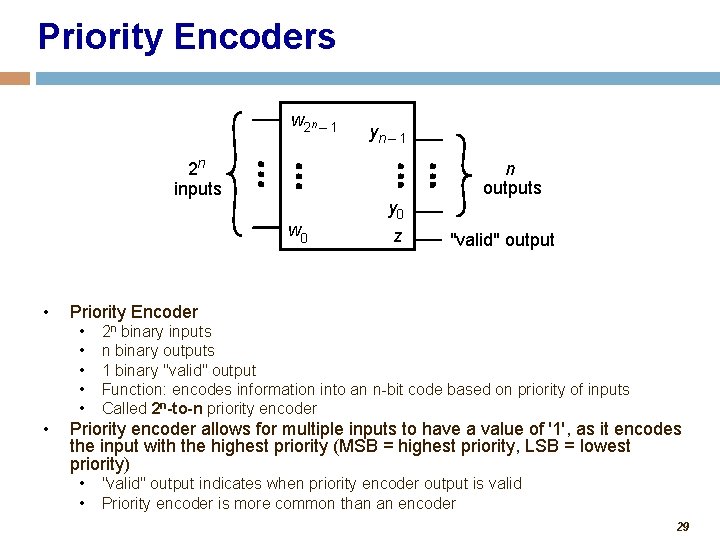
Priority Encoders w 2 n – 1 2 n inputs w 0 • y 0 z n outputs "valid" output Priority Encoder • • • yn – 1 2 n binary inputs n binary outputs 1 binary "valid" output Function: encodes information into an n-bit code based on priority of inputs Called 2 n-to-n priority encoder Priority encoder allows for multiple inputs to have a value of '1', as it encodes the input with the highest priority (MSB = highest priority, LSB = lowest priority) • • "valid" output indicates when priority encoder output is valid Priority encoder is more common than an encoder 29

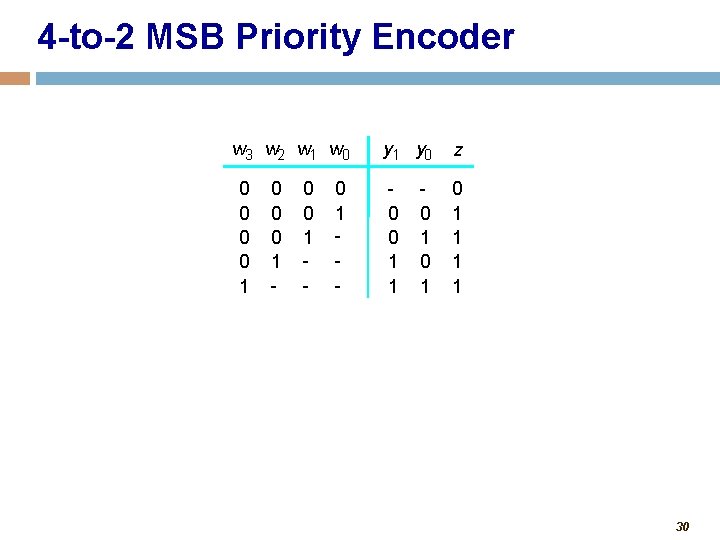
4 -to-2 MSB Priority Encoder w 3 w 2 w 1 w 0 0 0 1 - 0 1 - y 1 y 0 z 0 0 1 1 1 1 0 1 30

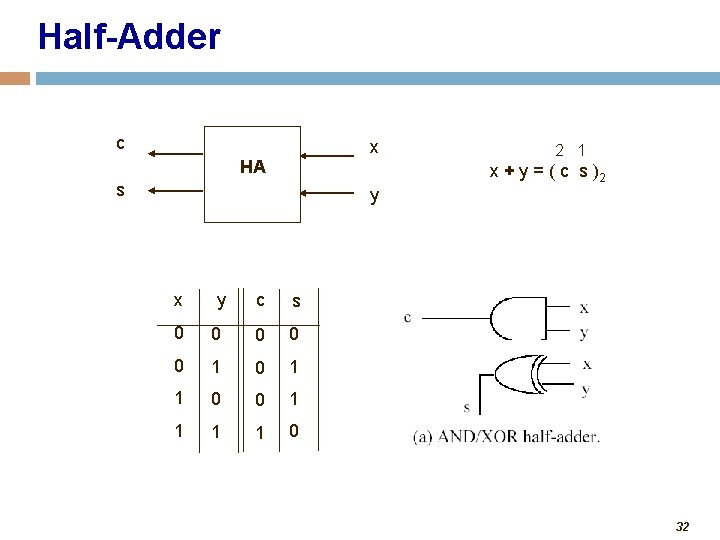
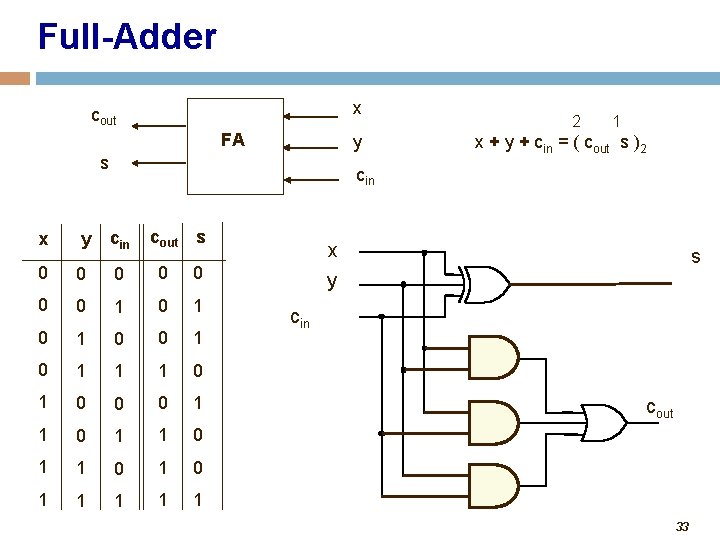
Single-Bit Adders • Half-adder • Adds two binary (i. e. 1 -bit) inputs A and B • Produces a sum and carryout • Problem: Cannot use it alone to build larger adders • Full-adder • Adds three binary (i. e. 1 -bit) inputs A, B, and carryin • Like half-adder, produces a sum and carryout • Allows building M-bit adders (M > 1) • Simple technique • Connect Cout of one adder to Cin of the next • These are called ripple-carry adders 31

Half-Adder c x HA 2 1 x + y = ( c s )2 s y x y c s 0 0 0 1 1 0 32

Full-Adder x cout FA y s 2 1 x + y + cin = ( cout s )2 cin cout s x y cin 0 0 0 0 1 0 1 0 1 1 1 0 0 0 1 1 0 1 1 1 x s y cin cout 33

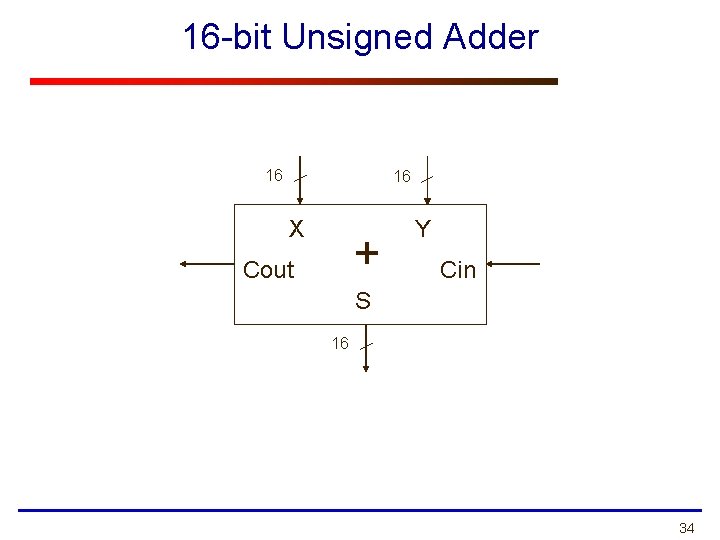
16 -bit Unsigned Adder 16 16 X + Cout Y Cin S 16 34

Multi-Bit Ripple-Carry Adder A 16 -bit ripple-carry adder is composed of 16 (1 -bit) full adders Inputs: 16 -bit A, 16 -bit B, 1 -bit carry in (set to zero in the figure below) Outputs: 16 -bit sum S, 1 -bit carry out Other multi-bit adder structures can be studied in ECE 645—Computer Arithmetic Called a ripple-carry adder because carry ripples from one full-adder to the next. Critical path is 16 full-adders. 35

Comparator • Used two compare two M-bit numbers and produce a flag (M >1) • Inputs: M-bit input A, M-bit input B • Output: 1 -bit output flag • 1 indicates condition is met • 0 indicates condition is not met • Can compare: >, >=, <, <=, =, etc. A B M M A > B? 1 if A > B 0 if A <= B 36

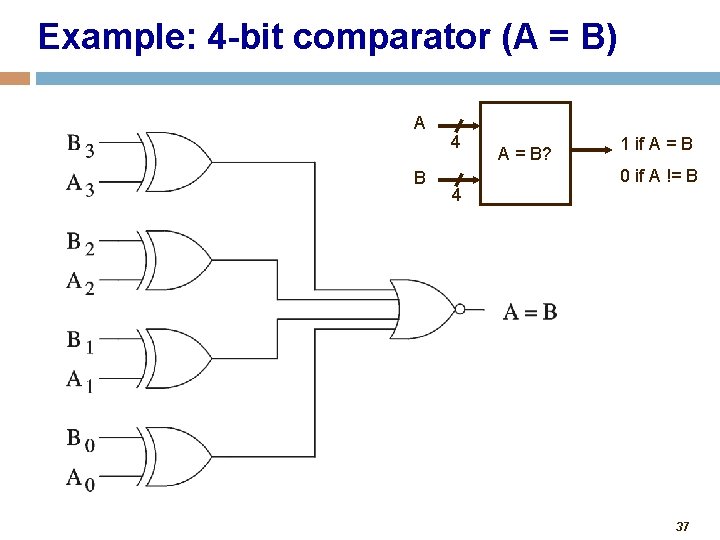
Example: 4 -bit comparator (A = B) A B 4 4 A = B? 1 if A = B 0 if A != B 37

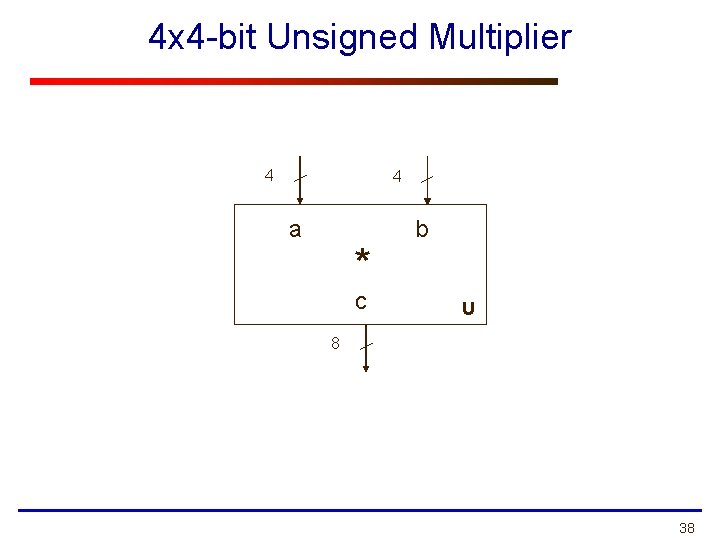
4 x 4 -bit Unsigned Multiplier 4 4 a * c b U 8 38

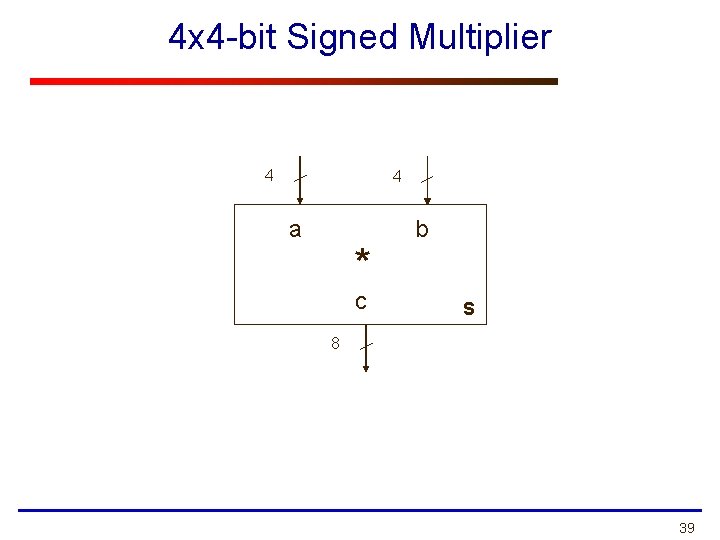
4 x 4 -bit Signed Multiplier 4 4 a * c b S 8 39

Unsigned vs. Signed Multiplication Unsigned Signed 1111 x 1111 15 x 15 1111 x 1111 -1 x -1 11100001 225 00000001 1 40

Quotient and remainder Given integers a and n, n>0 ! q, r Z such that a = q n + r and 0 r<n q – quotient a q= n r – remainder (of a divided by n) a r = a - q n = a – n = a mod n = a div n 41

Rules of addition, subtraction and multiplication modulo n a + b mod n = ((a mod n) + (b mod n)) mod n a - b mod n = ((a mod n) - (b mod n)) mod n a b mod n = ((a mod n) (b mod n)) mod n 42

Logical Shift Right A(3) A(2) A(1) A(0) 4 A A >>1 L C C 4 ‘ 0’ A(3) A(2) A(1) 43

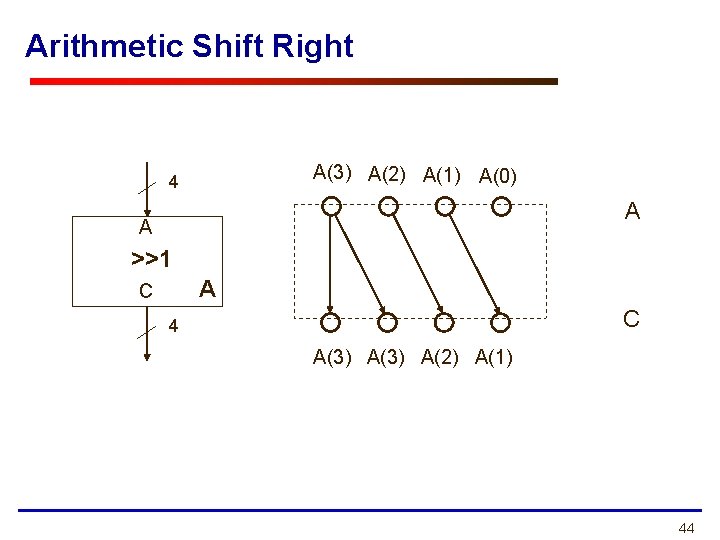
Arithmetic Shift Right A(3) A(2) A(1) A(0) 4 A A >>1 A C C 4 A(3) A(2) A(1) 44

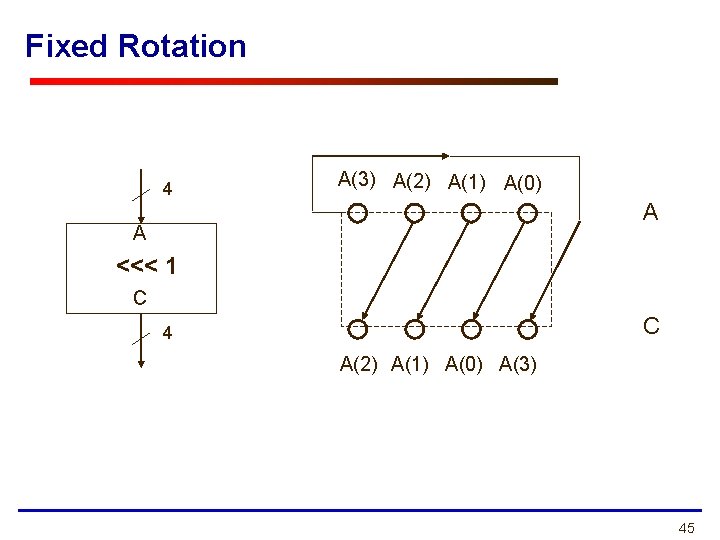
Fixed Rotation 4 A(3) A(2) A(1) A(0) A A <<< 1 C C 4 A(2) A(1) A(0) A(3) 45

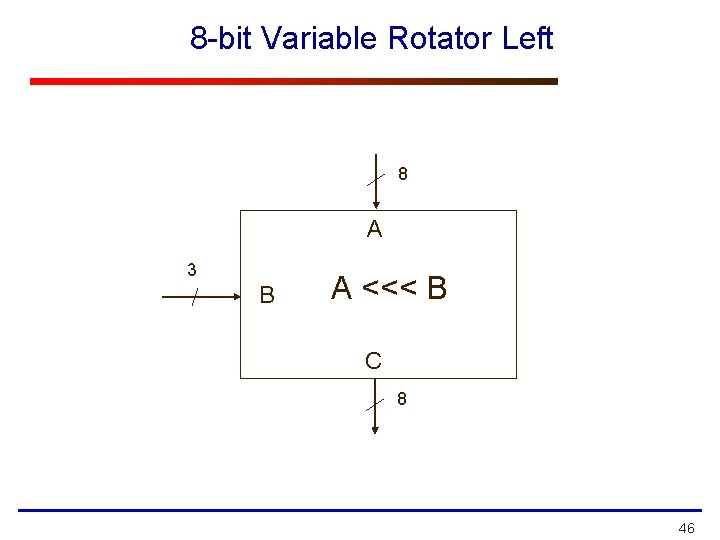
8 -bit Variable Rotator Left 8 A 3 B A <<< B C 8 46

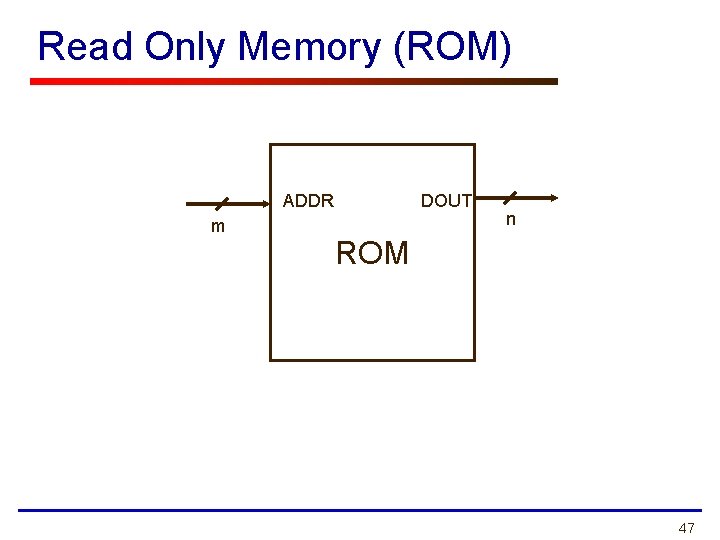
Read Only Memory (ROM) ADDR m DOUT n ROM 47

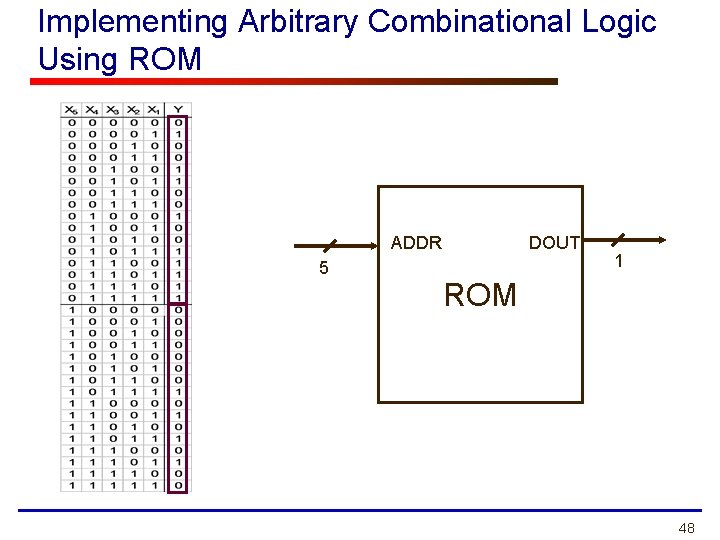
Implementing Arbitrary Combinational Logic Using ROM ADDR 5 DOUT 1 ROM 48

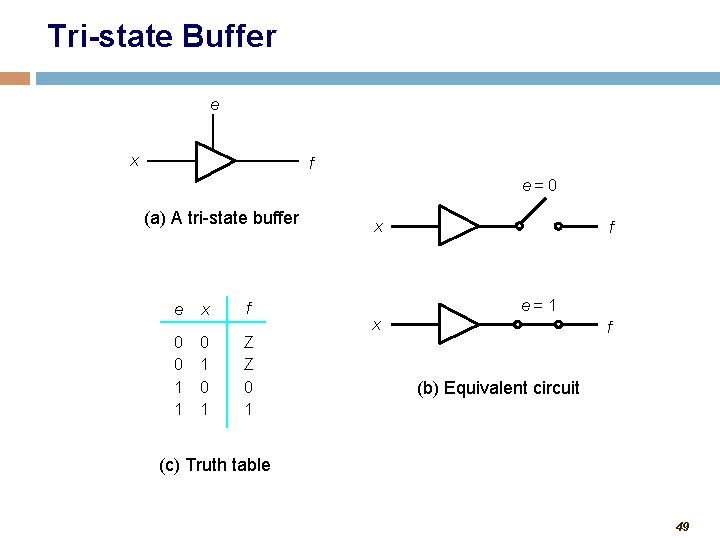
Tri-state Buffer e x f e= 0 (a) A tri-state buffer e x f 0 0 1 1 Z Z 0 1 0 1 x x f e= 1 f (b) Equivalent circuit (c) Truth table 49

Four types of Tri-state Buffers 50