Dynamic Programming David Kauchak cs 161 Summer 2009

Dynamic Programming David Kauchak cs 161 Summer 2009

Administrative l Final exam next week! (9/14 3: 30 pm – 6: 30 pm) l l Review session 9/10 lecture l l linear programming network flow problems Map reduce algorithms in popular media

Dynamic programming l l One of the most important algorithm tools! Very common interview question Method for solving problems where optimal solutions can be defined in terms of optimal solutions to sub-problems AND the sub-problems are overlapping

Fibonacci numbers l 1, 1, 2, 3, 5, 8, 13, 21, 34, … What is the recurrence for the nth Fibonacci number? l F(n) = F(n-1) + F(n-2) l The solution for n is defined with respect to the solution to smaller problems (n-1 and n-2) l

Fibonacci: a first attempt

Is it correct? F(n) = F(n-1) + F(n-2)

Running time l l Each call creates two recursive calls Each call reduces the size of the problem by 1 or 2 Creates a full binary of depth n O(2 n)

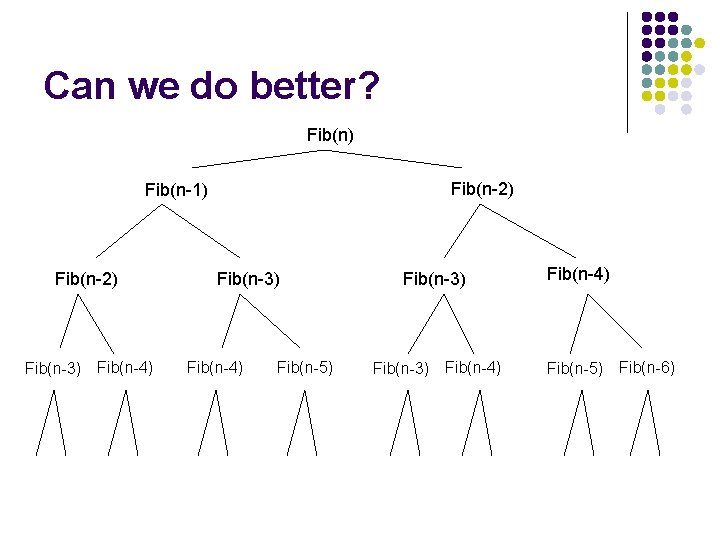
Can we do better? Fib(n) Fib(n-2) Fib(n-1) Fib(n-2) Fib(n-3) Fib(n-4) Fib(n-5) Fib(n-6)

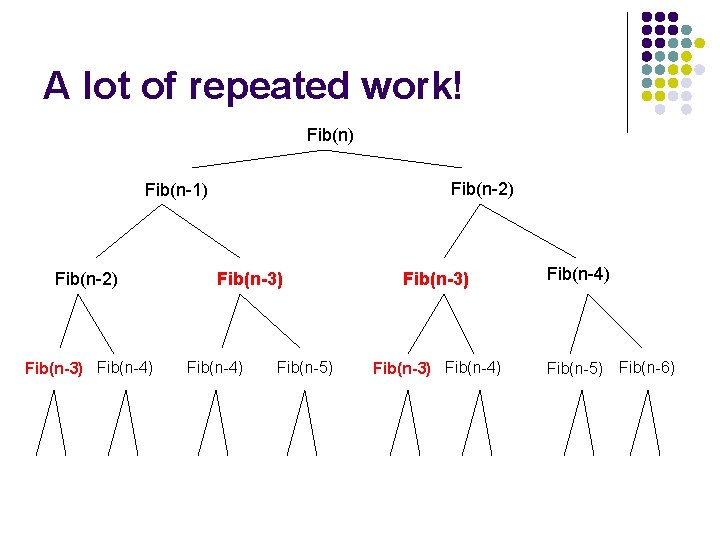
A lot of repeated work! Fib(n) Fib(n-2) Fib(n-1) Fib(n-2) Fib(n-3) Fib(n-4) Fib(n-5) Fib(n-6)

Identifying a dynamic programming problem l The solution can be defined with respect to solutions to subproblems l The subproblems created are overlapping, that is we see the same subproblems repeated

Two main ideas for dynamic programming l Identify a solution to the problem with respect to smaller subproblems l l F(n) = F(n-1) + F(n-2) Bottom up: start with solutions to the smallest problems and build solutions to the larger problems use an array to store solutions to subproblems

Is it correct? F(n) = F(n-1) + F(n-2)

Running time? Θ(n)

Counting binary search trees l How many unique binary search trees can be created using the numbers 1 through n? 4 2 1 5 3 6

Step 1: What is the subproblem? l l l 1 Assume we have some black box solver (call it T) that can give us the answer to smaller subproblems How can we use the answer from this to answer our question? How many options for the root are there? 2 3 … n

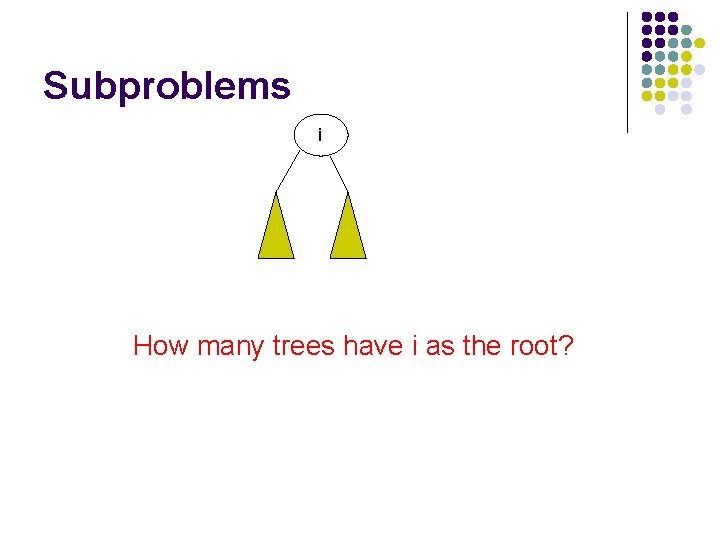
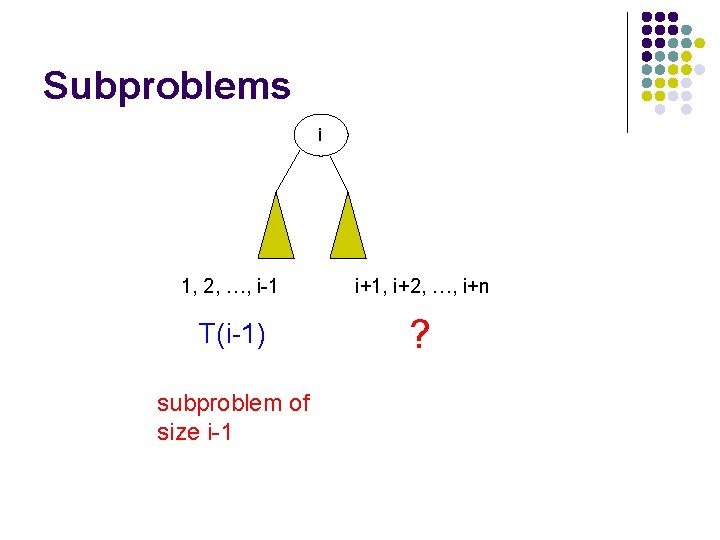
Subproblems i How many trees have i as the root?

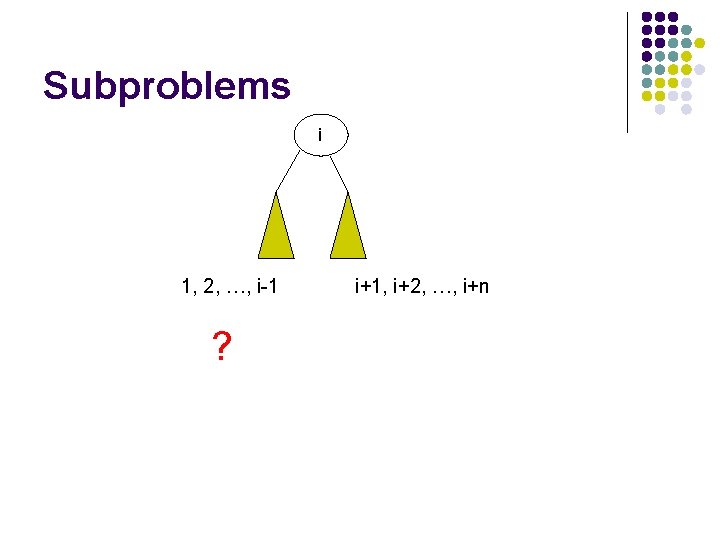
Subproblems i 1, 2, …, i-1 ? i+1, i+2, …, i+n

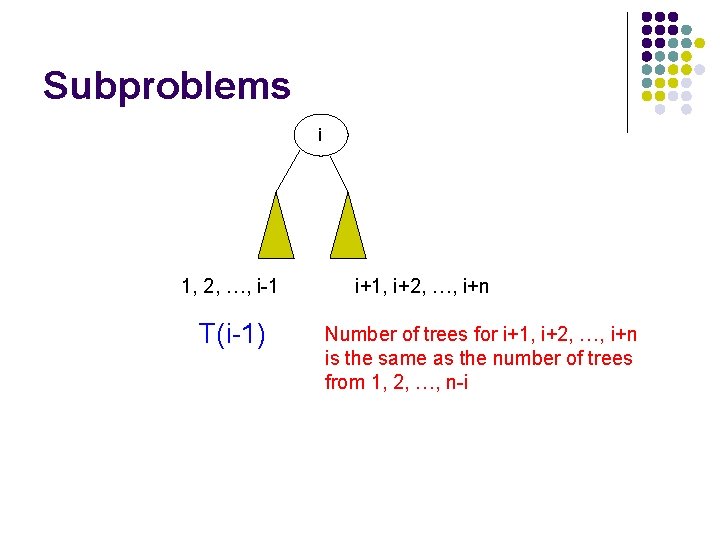
Subproblems i 1, 2, …, i-1 i+1, i+2, …, i+n T(i-1) ? subproblem of size i-1

Subproblems i 1, 2, …, i-1 T(i-1) i+1, i+2, …, i+n Number of trees for i+1, i+2, …, i+n is the same as the number of trees from 1, 2, …, n-i

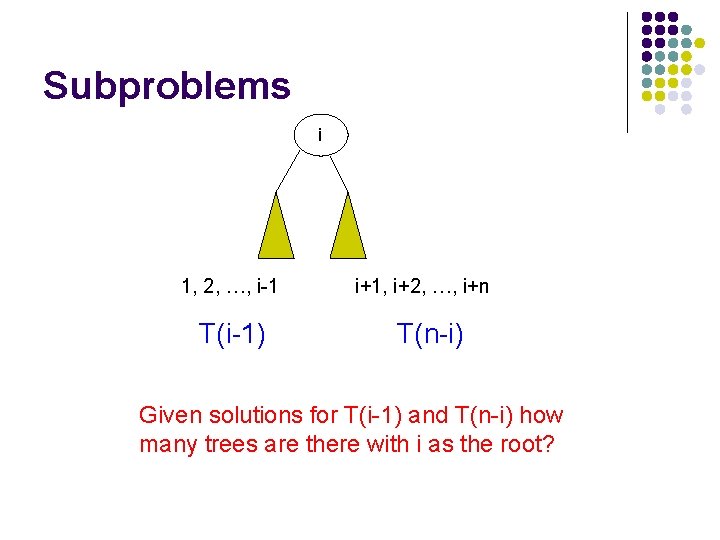
Subproblems i 1, 2, …, i-1 T(i-1) i+1, i+2, …, i+n T(n-i) Given solutions for T(i-1) and T(n-i) how many trees are there with i as the root?

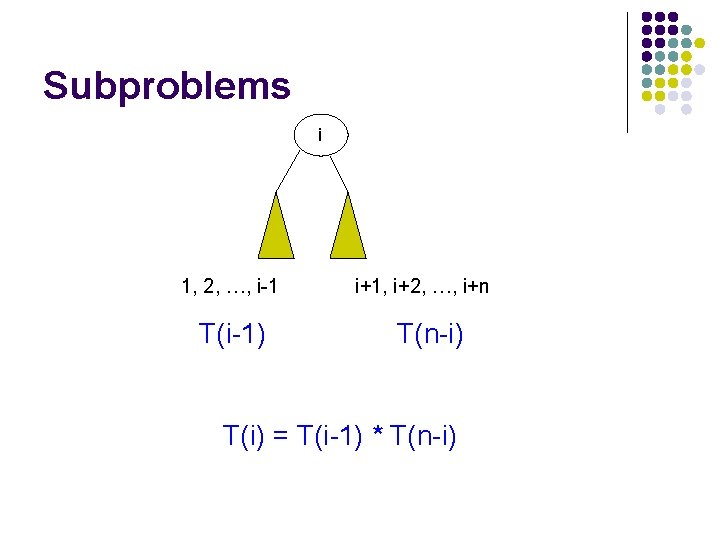
Subproblems i 1, 2, …, i-1 T(i-1) i+1, i+2, …, i+n T(n-i) T(i) = T(i-1) * T(n-i)

Step 1: Defining the answer with respect to subproblems T(i) = T(i-1) * T(n-i)

Is there a problem? As with Fibonacci, we’re repeating a lot of work

Step 2: Generate a solution from the bottom-up

0 1 2 3 4 5 … n

1 1 0 1 2 3 4 5 … n

c[0]*c[1] + c[1]*c[0] 1 1 0 1 2 3 4 5 … n

1 2 2 1 c[0]*c[1] + c[1]*c[0] 1 1 0 1 2 3 4 5 … n

1 1 2 0 1 2 3 4 5 … n

1 2 3 c[0]*c[2] + c[1]*c[1] + c[2]*c[0] 1 1 2 0 1 2 3 4 5 … n

1 1 2 5 0 1 2 3 4 5 … n

1 1 2 5 … 0 1 2 3 4 5 … n

Running time? Θ(n 2)

0 -1 Knapsack problem l l 0 -1 Knapsack – A thief robbing a store finds n items worth v 1, v 2, . . , vn dollars and weight w 1, w 2, …, wn pounds, where vi and wi are integers. The thief can carry at most W pounds in the knapsack. Which items should the thief take if he wants to maximize value. Repetitions are allowed, that is you can take multiple copies of any item

Longest common subsequence (LCS) l For a sequence X = x 1, x 2, …, xn, a subsequence is a subset of the sequence defined by a set of increasing indices (i 1, i 2, …, ik) where 1 ≤ i 1 < i 2 < … < ik ≤ n X=ABACDABAB ABA?

Longest common subsequence (LCS) l For a sequence X = x 1, x 2, …, xn, a subsequence is a subset of the sequence defined by a set of increasing indices (i 1, i 2, …, ik) where 1 ≤ i 1 < i 2 < … < ik ≤ n X=ABACDABAB ABA

Longest common subsequence (LCS) l For a sequence X = x 1, x 2, …, xn, a subsequence is a subset of the sequence defined by a set of increasing indices (i 1, i 2, …, ik) where 1 ≤ i 1 < i 2 < … < ik ≤ n X=ABACDABAB ACA?

Longest common subsequence (LCS) l For a sequence X = x 1, x 2, …, xn, a subsequence is a subset of the sequence defined by a set of increasing indices (i 1, i 2, …, ik) where 1 ≤ i 1 < i 2 < … < ik ≤ n X=ABACDABAB ACA

Longest common subsequence (LCS) l For a sequence X = x 1, x 2, …, xn, a subsequence is a subset of the sequence defined by a set of increasing indices (i 1, i 2, …, ik) where 1 ≤ i 1 < i 2 < … < ik ≤ n X=ABACDABAB DCA?

Longest common subsequence (LCS) l For a sequence X = x 1, x 2, …, xn, a subsequence is a subset of the sequence defined by a set of increasing indices (i 1, i 2, …, ik) where 1 ≤ i 1 < i 2 < … < ik ≤ n X=ABACDABAB DCA

Longest common subsequence (LCS) l For a sequence X = x 1, x 2, …, xn, a subsequence is a subset of the sequence defined by a set of increasing indices (i 1, i 2, …, ik) where 1 ≤ i 1 < i 2 < … < ik ≤ n X=ABACDABAB AADAA?

Longest common subsequence (LCS) l For a sequence X = x 1, x 2, …, xn, a subsequence is a subset of the sequence defined by a set of increasing indices (i 1, i 2, …, ik) where 1 ≤ i 1 < i 2 < … < ik ≤ n X=ABACDABAB AADAA

LCS problem l l Given two sequences X and Y, a common subsequence is a subsequence that occurs in both X and Y Given two sequences X = x 1, x 2, …, xn and Y = y 1, y 2, …, yn, What is the longest common subsequence? X=ABCBDAB Y=BDCABA

LCS problem l l Given two sequences X and Y, a common subsequence is a subsequence that occurs in both X and Y Given two sequences X = x 1, x 2, …, xn and Y = y 1, y 2, …, yn, What is the longest common subsequence? X=ABCBDAB Y=BDCABA

Step 1: Define the problem with respect to subproblems X=ABCBDAB Y=BDCABA

Step 1: Define the problem with respect to subproblems X=ABCBDA? Y=BDCAB? Is the last character part of the LCS?

Step 1: Define the problem with respect to subproblems X=ABCBDA? Y=BDCAB? Two cases: either the characters are the same or they’re different

Step 1: Define the problem with respect to subproblems X=ABCBDAA LCS Y=BDCABA If they’re the same The characters are part of the LCS

Step 1: Define the problem with respect to subproblems X=ABCBDAB LCS Y=BDCABA If they’re different

Step 1: Define the problem with respect to subproblems X=ABCBDAB LCS Y=BDCABA If they’re different

Step 1: Define the problem with respect to subproblems X=ABCBDAB Y=BDCABA If they’re different ?

Step 1: Define the problem with respect to subproblems X=ABCBDAB Y=BDCABA

Step 2: Build the solution from the bottom up What types of subproblem solutions do we need to store? LCS(X 1…j, Y 1…k) two different indices

Step 2: Build the solution from the bottom up What types of subproblem solutions do we need to store? LCS(X 1…j, Y 1…k)

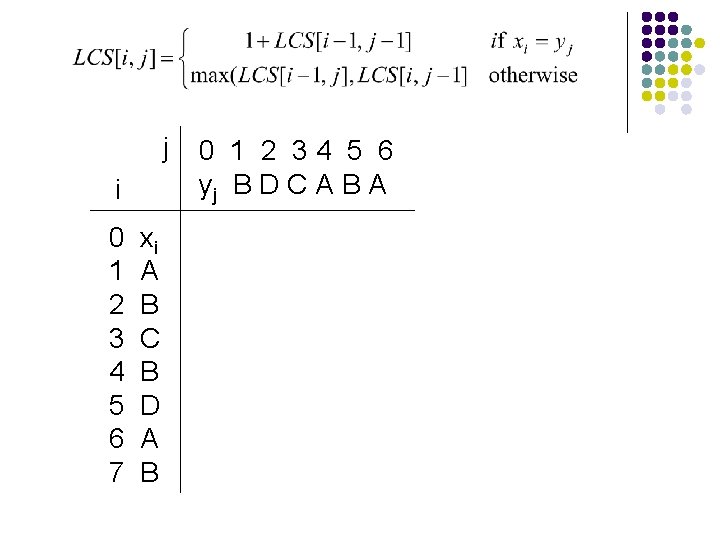
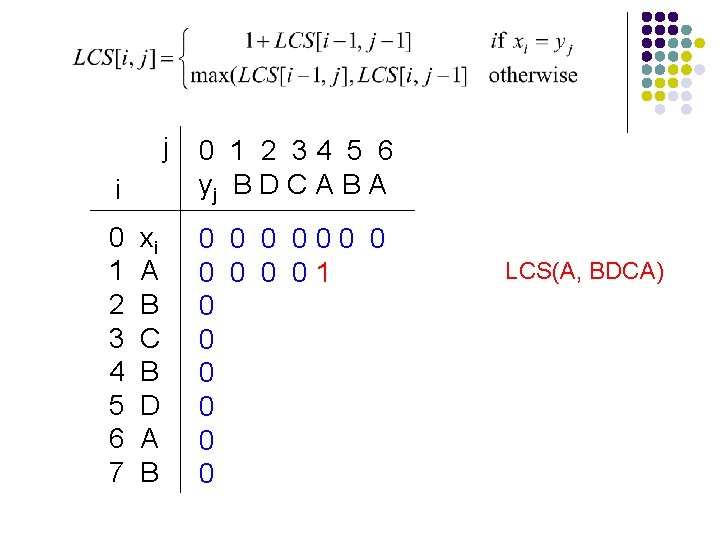
j i 0 1 2 3 4 5 6 7 xi A B C B D A B 0 1 2 34 5 6 yj B D C A B A

j i 0 1 2 3 4 5 6 7 xi A B C B D A B 0 1 2 34 5 6 yj B D C A B A 0 000 0 0 0 0

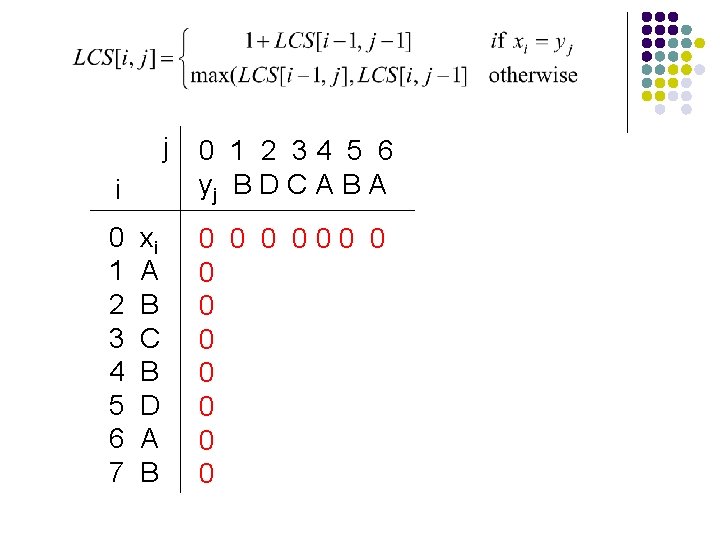
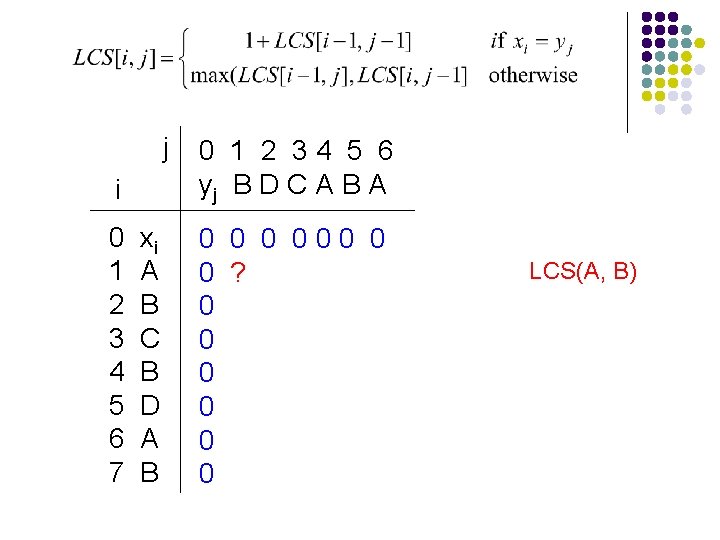
j i 0 1 2 3 4 5 6 7 xi A B C B D A B 0 1 2 34 5 6 yj B D C A B A 0 000 0 0 ? 0 0 0 LCS(A, B)

j i 0 1 2 3 4 5 6 7 xi A B C B D A B 0 1 2 34 5 6 yj B D C A B A 0 000 0 0 0 0

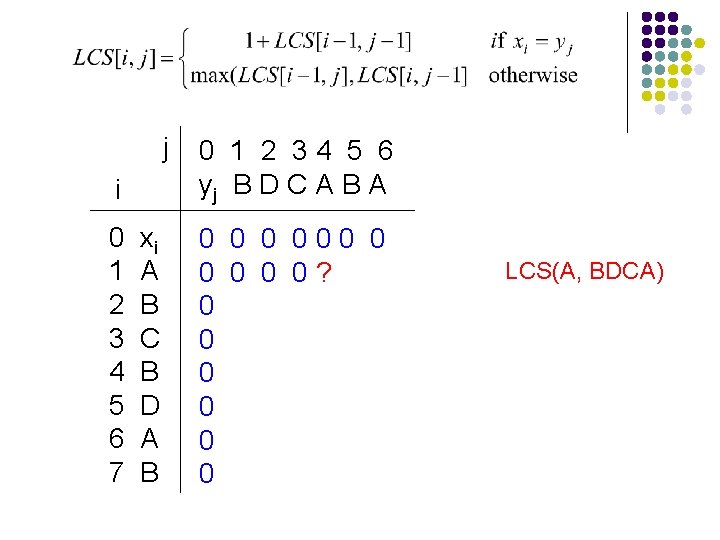
j i 0 1 2 3 4 5 6 7 xi A B C B D A B 0 1 2 34 5 6 yj B D C A B A 0 000 0 0 0? 0 0 0 LCS(A, BDCA)

j i 0 1 2 3 4 5 6 7 xi A B C B D A B 0 1 2 34 5 6 yj B D C A B A 0 000 0 0 01 0 0 0 LCS(A, BDCA)

j i 0 1 2 3 4 5 6 7 xi A B C B D A B 0 1 2 34 5 6 yj B D C A B A 0 0 0 0 0 1 1 1 000 011 112 22? 0 1 2 2 LCS(ABCB, BDCAB)

j i 0 1 2 3 4 5 6 7 xi A B C B D A B 0 1 2 34 5 6 yj B D C A B A 0 0 0 0 0 1 1 1 000 011 112 223 0 1 2 2 LCS(ABCB, BDCAB)

j i 0 1 2 3 4 5 6 7 xi A B C B D A B 0 1 2 34 5 6 yj B D C A B A 0 0 0 0 0 1 1 1 2 2 2 000 011 112 223 223 234 0 1 2 2 3 3 4 4 Where’s the final answer?

The algorithm

The algorithm Base case initialization

The algorithm Fill in the matrix

The algorithm

The algorithm

The algorithm

Running time? Θ(nm)

Keeping track of the solution l l l Our LCS algorithm only calculated the length of the LCS between X and Y What if we wanted to know the actual sequence? Keep track of this as well…

j i 0 1 2 3 4 5 6 7 xi A B C B D A B 0 1 2 34 5 6 yj B D C A B A 0 0 0 0 0 1 1 1 2 2 2 000 011 112 223 223 234 0 1 2 2 3 3 4 4 We can follow the arrows to generate the solution

j i 0 1 2 3 4 5 6 7 xi A B C B D A B 0 1 2 34 5 6 yj B D C A B A 0 0 0 0 0 1 1 1 2 2 2 000 011 112 223 223 234 0 1 2 2 3 3 4 4 We can follow the arrows to generate the solution BCBA

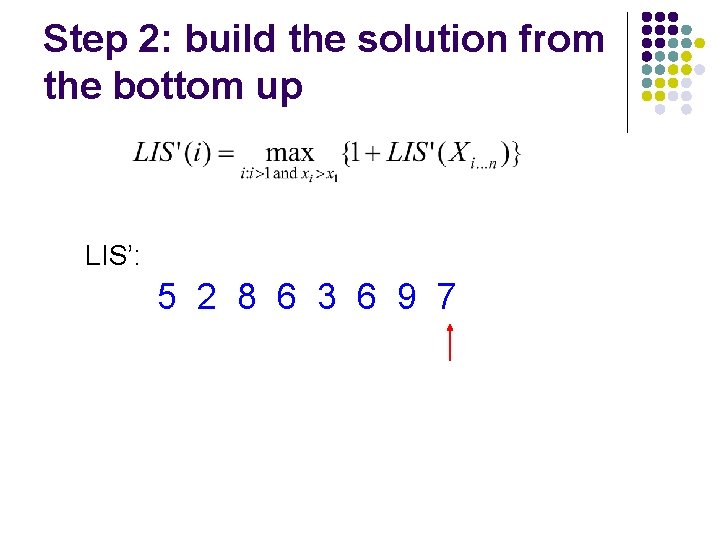
Longest increasing subsequence l Given a sequence of numbers X = x 1, x 2, …, xn find the longest increasing subsequence (i 1, i 2, …, ik), that is a subsequence where numbers in the sequence increase. 5 2 8 6 3 6 9 7

Longest increasing subsequence l Given a sequence of numbers X = x 1, x 2, …, xn find the longest increasing subsequence (i 1, i 2, …, ik), that is a subsequence where numbers in the sequence increase. 5 2 8 6 3 6 9 7

Step 1: Define the problem with respect to subproblems 5 2 8 6 3 6 9 7 Two options: Either 5 is in the LIS or it’s not

Step 1: Define the problem with respect to subproblems 5 2 8 6 3 6 9 7 include 5 5 + LIS(8 6 3 6 9 7) 5 + LIS(6 9 7) 5 + LIS(7)

Step 1: Define the problem with respect to subproblems 5 2 8 6 3 6 9 7 don’t include 5 LIS(2 8 6 3 6 9 7)

Step 1: Define the problem with respect to subproblems l Be sure to be clear how you define your recursive subproblems don’t include LIS: longest increasing sequence for elements xi…n include LIS: longest increasing sequence starting at element i (i. e. must include i)

Step 1: Define the problem with respect to subproblems Longest increasing sequence starting at i Longest increasing sequence for X is the longest increasing sequence starting at any element

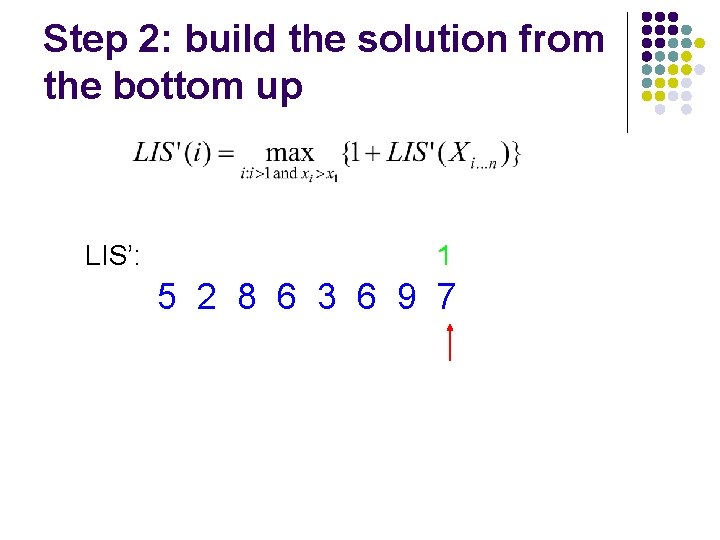
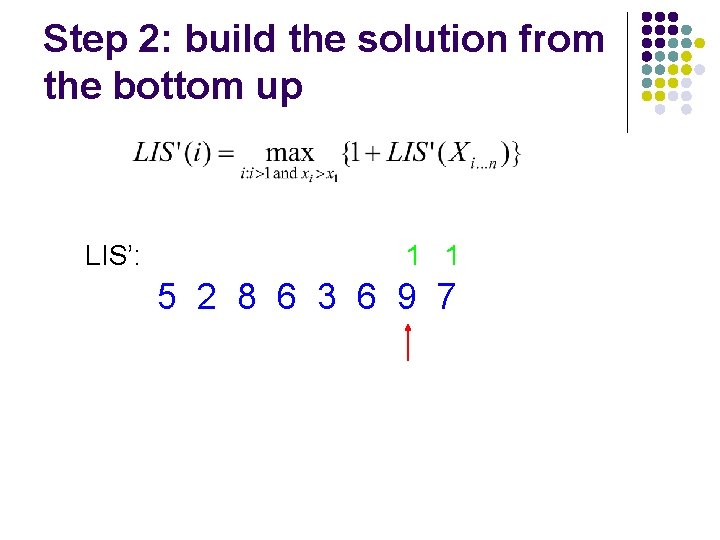
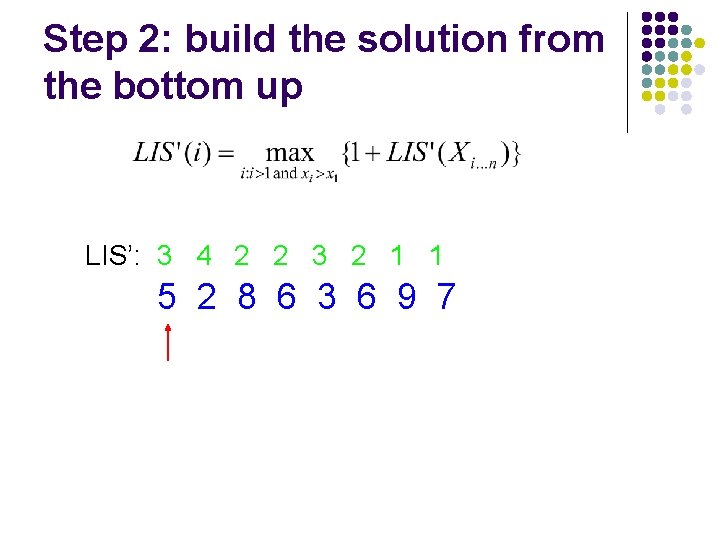
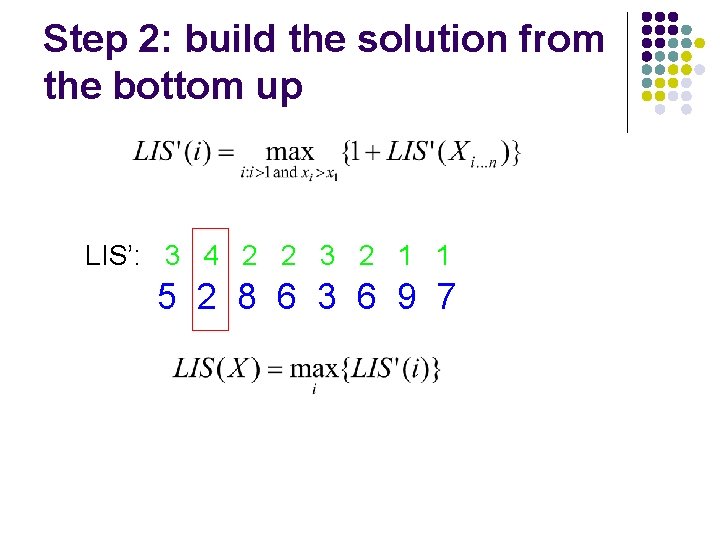
Step 2: build the solution from the bottom up LIS’: 5 2 8 6 3 6 9 7

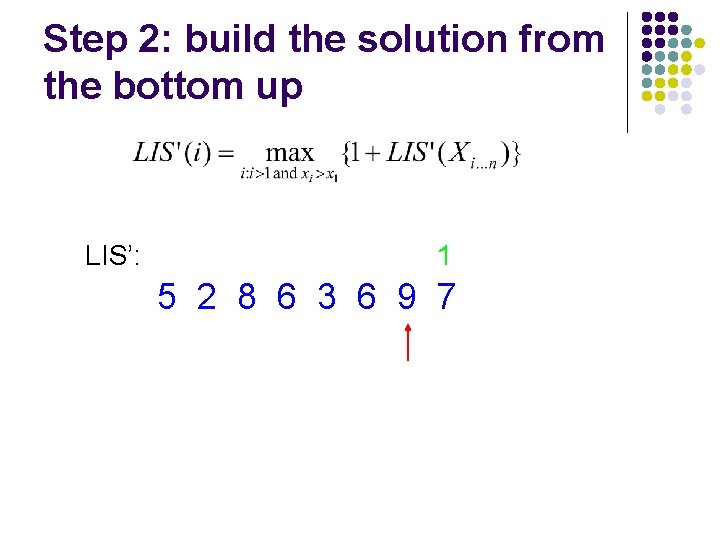
Step 2: build the solution from the bottom up LIS’: 1 5 2 8 6 3 6 9 7

Step 2: build the solution from the bottom up LIS’: 1 5 2 8 6 3 6 9 7

Step 2: build the solution from the bottom up LIS’: 1 1 5 2 8 6 3 6 9 7

Step 2: build the solution from the bottom up LIS’: 1 1 5 2 8 6 3 6 9 7

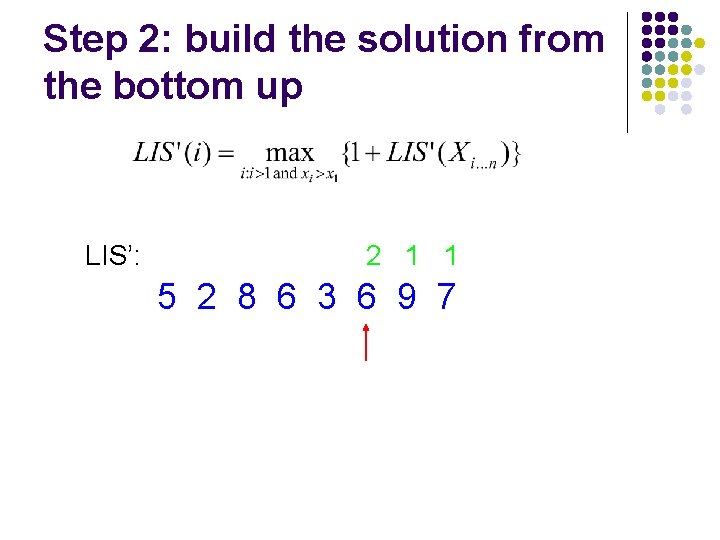
Step 2: build the solution from the bottom up LIS’: 2 1 1 5 2 8 6 3 6 9 7

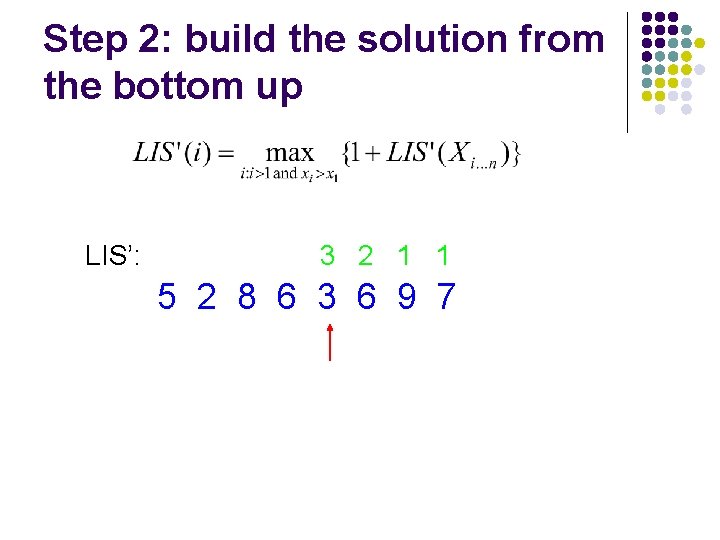
Step 2: build the solution from the bottom up LIS’: 3 2 1 1 5 2 8 6 3 6 9 7

Step 2: build the solution from the bottom up LIS’: 2 3 2 1 1 5 2 8 6 3 6 9 7

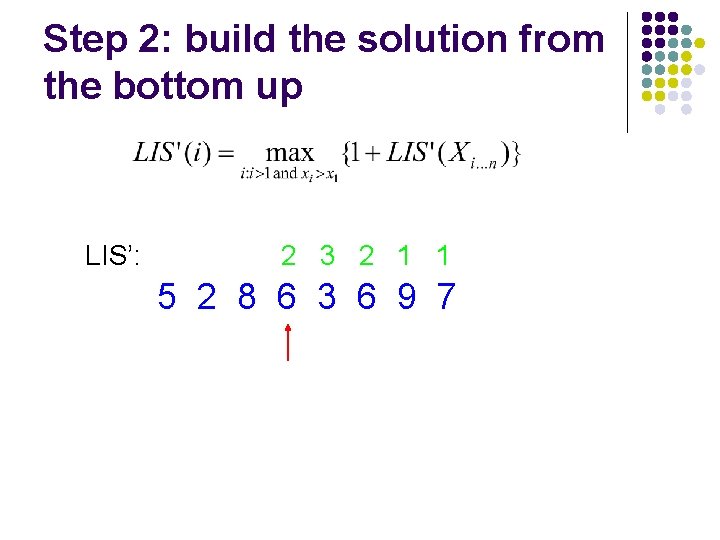
Step 2: build the solution from the bottom up LIS’: 2 2 3 2 1 1 5 2 8 6 3 6 9 7

Step 2: build the solution from the bottom up LIS’: 4 2 2 3 2 1 1 5 2 8 6 3 6 9 7

Step 2: build the solution from the bottom up LIS’: 3 4 2 2 3 2 1 1 5 2 8 6 3 6 9 7

Step 2: build the solution from the bottom up LIS’: 3 4 2 2 3 2 1 1 5 2 8 6 3 6 9 7

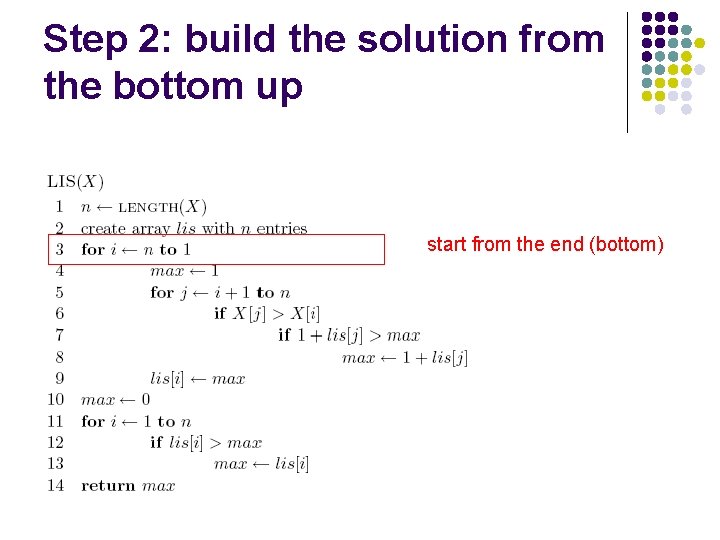
Step 2: build the solution from the bottom up

Step 2: build the solution from the bottom up start from the end (bottom)

Step 2: build the solution from the bottom up

Step 2: build the solution from the bottom up

Step 2: build the solution from the bottom up initialization?

Running time? Θ(n 2)

Another solution l Can we use LCS to solve this problem? 5 2 8 6 3 6 9 7 LCS 2 3 5 6 6 7 8 9

Another solution l Can we use LCS to solve this problem? 5 2 8 6 3 6 9 7 LCS 2 3 5 6 6 7 8 9

Memoization l l Sometimes it can be a challenge to write the function in a bottom-up fashion Memoization: l l Write the recursive function top-down Alter the function to check if we’ve already calculated the value If so, use the pre-calculate value If not, do the recursive call(s)

Memoized fibonacci

Memoized fibonacci

Memoized fibonacci Use to denote uncalculated

Memoized fibonacci What else could we use besides an array? Use to denote uncalculated

Memoized fibonacci Check if we already calculated the value

Memoized fibonacci calculate the value

Memoized fibonacci store the value

Memoization l Pros l l l Can be more intuitive to code/understand Can be memory savings if you don’t need answers to all subproblems Cons l Larger overhead because of recursion

Quick summary l Step 1: Define the problem with respect to subproblems l l l We did this for divide and conquer too. What’s the difference? You can identify a candidate for dynamic programming if there is overlap or repeated work in the subproblems being created Step 2: build the solution from the bottom up l l Build the solution such that the subproblems referenced by larger problems are already solved Memoization is also an alternative