DelayOptimal Scheduling for Data Center Networks and Input

Delay-Optimal Scheduling for Data Center Networks and Input Queued Switches in Heavy Traffic Siva Theja Maguluri, IBM T. J. Watson Research Center R. Srikant, UIUC Sai Kiran Burle, UIUC 1

Cloud Computing • Computing as a utility • Economies of scale • Emergence of Big data 2

Data Center Web Pages Documents Files Audios Videos Pictures 3

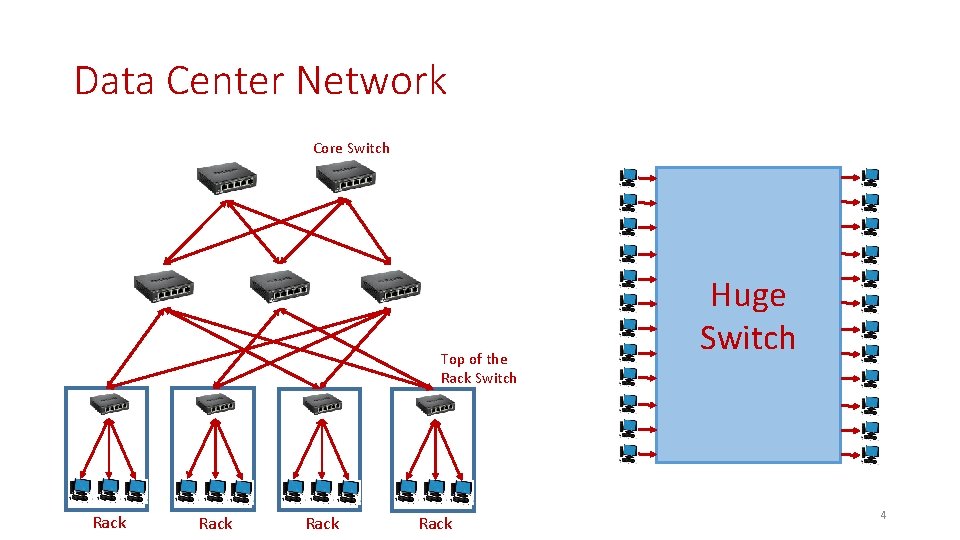
Data Center Network Core Switch Top of the Rack Switch Rack Huge Switch 4

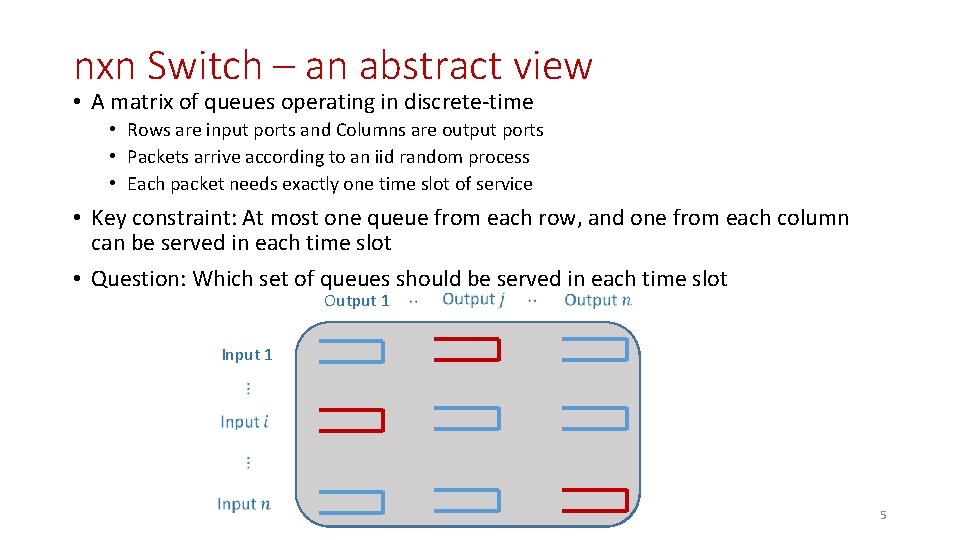
nxn Switch – an abstract view • A matrix of queues operating in discrete-time • Rows are input ports and Columns are output ports • Packets arrive according to an iid random process • Each packet needs exactly one time slot of service • Key constraint: At most one queue from each row, and one from each column can be served in each time slot • Question: Which set of queues should be served in each time slot Output 1 Input 1 5

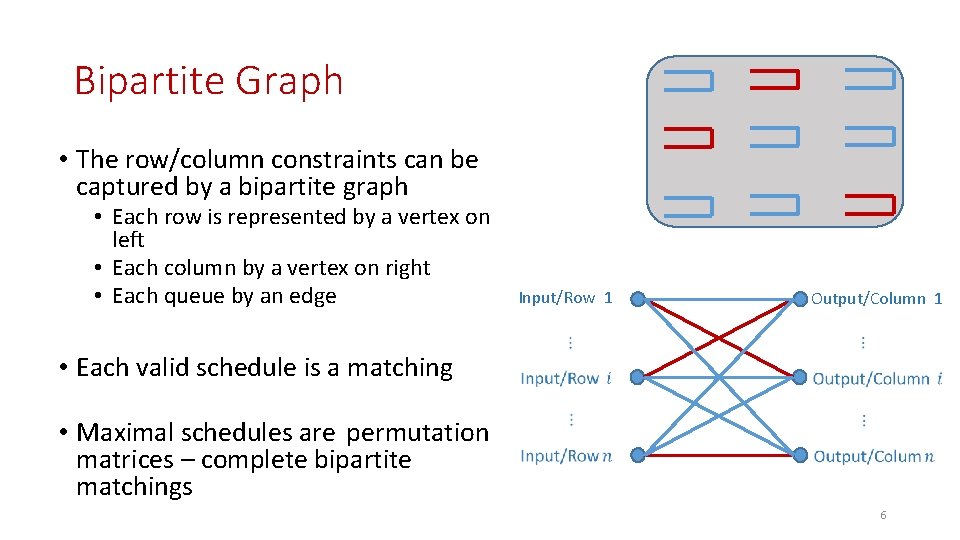
Bipartite Graph • The row/column constraints can be captured by a bipartite graph • Each row is represented by a vertex on left • Each column by a vertex on right • Each queue by an edge • Each valid schedule is a matching • Maximal schedules are permutation matrices – complete bipartite matchings Input/Row 1 Output/Column 1 6

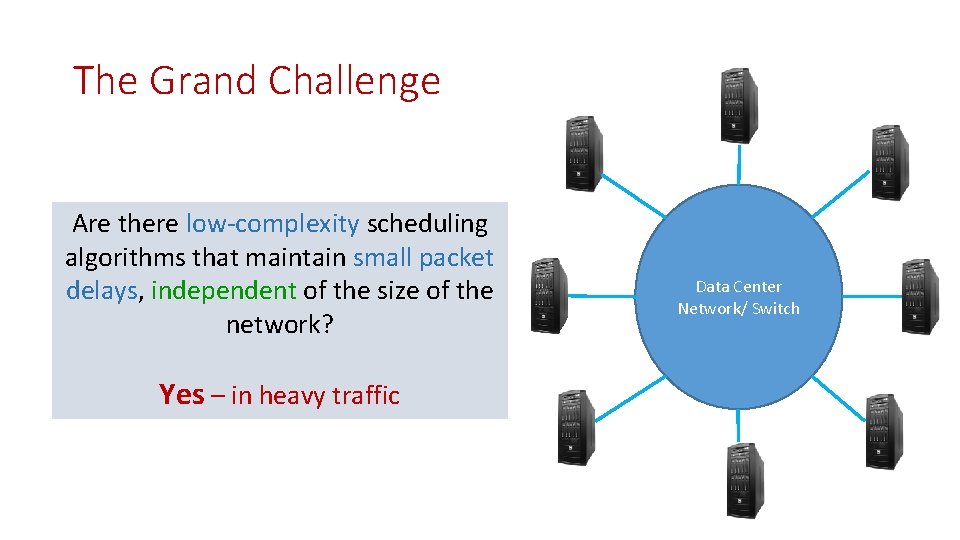
The Grand Challenge Are there low-complexity scheduling algorithms that maintain small packet delays, independent of the size of the network? Yes – in heavy traffic Data Center Network/ Switch

Capacity Region • 8

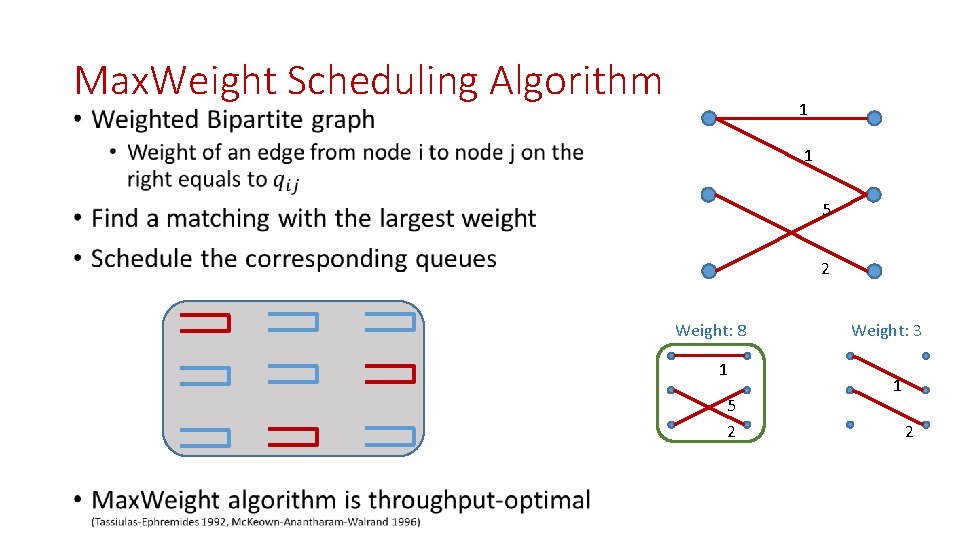
Max. Weight Scheduling Algorithm 1 • 1 5 2 Weight: 8 1 5 2 Weight: 3 1 2

Queue Length Scaling: Heavy Traffic • i. e. , 10

Heavy-Traffic Result • 11

Related Work • Heavy-traffic optimality under a condition called Complete Resource Pooling (CRP) • Stolyar (2004) • One-dimensional state-space collapse – Using Diffusion limit • Eryilmaz and Srikant (2012) • Lyapunov drift based argument • Three steps –Universal Lower bound, State space collapse under Max. Weight, Matching Upper bound • We use heavy traffic technique developed in this paper above • State-space collapse and Diffusion Limit without CRP • Andrews, Jung, and Stolyar (2007); Shah and Wischik (2012); Kang and Williams (2012) • Multi-dimensional state-space collapse • Other policies which achieve optimal or near-optimal scaling • Neely, Modiano and Cheng (2007); Shah, Walton and Zhong (2012); Shah, Tsitsiklis and 12 Zhong (2014)

Outline of the Proof • It’s all about unused service • Digression 1: Kingman bound for discrete-time single-server queue • Digression 2: Heavy-Traffic Optimality of the Join-the-Shortest-Queue (JSQ) Policy • Back to Heavy-Traffic Behavior of the Max. Weight Algorithm in a Switch 13

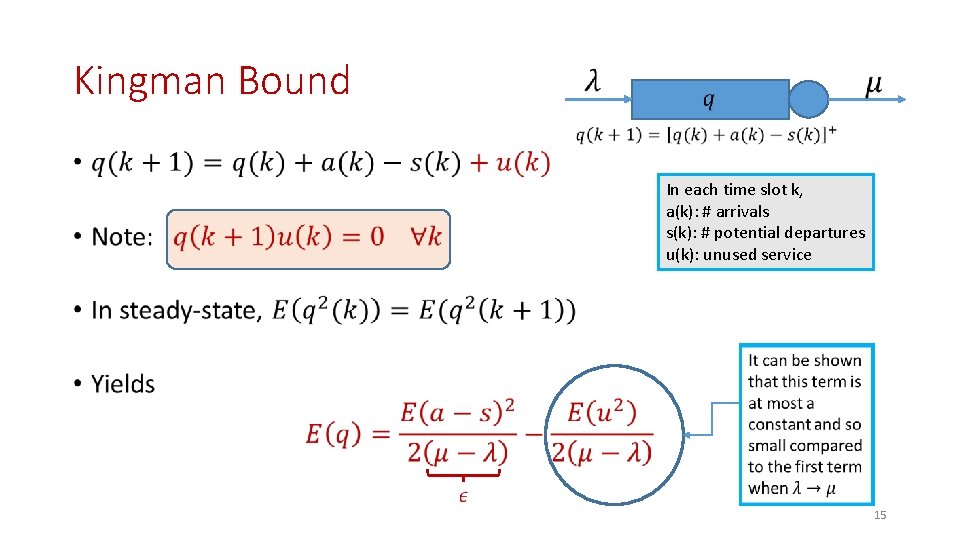
Kingman Bound for Single-Server Queues 14

Kingman Bound • In each time slot k, a(k): # arrivals s(k): # potential departures u(k): unused service 15

Key Fact About Unused Service • Main message of this talk: It is useful to view heavy-traffic theory as a generalization of this statement 16

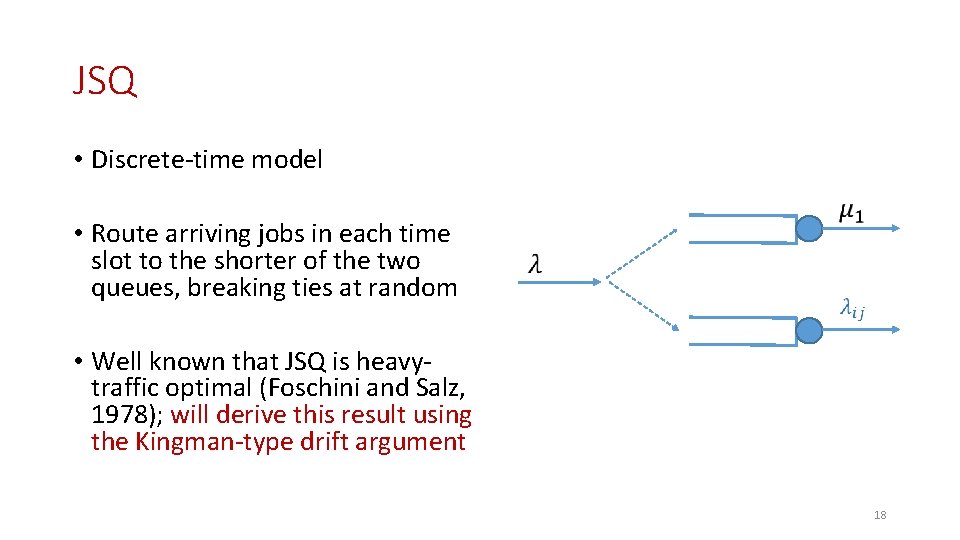
Join-the-Shortest-Queue Routing Policy 17

JSQ • Discrete-time model • Route arriving jobs in each time slot to the shorter of the two queues, breaking ties at random • Well known that JSQ is heavytraffic optimal (Foschini and Salz, 1978); will derive this result using the Kingman-type drift argument 18

Methodology • 19

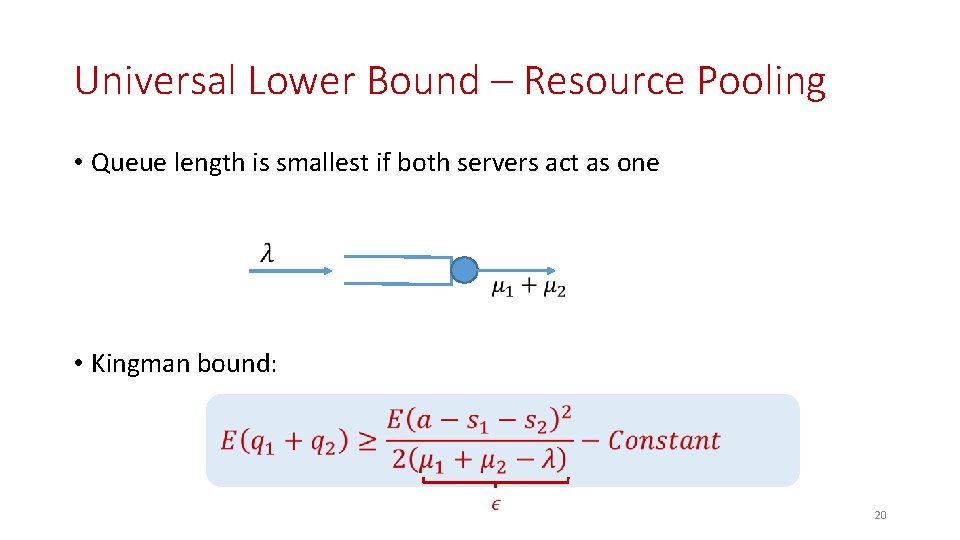
Universal Lower Bound – Resource Pooling • Queue length is smallest if both servers act as one • Kingman bound: 20

State-Space Collapse • 21

Matching Upper bound for JSQ • 22

Using State-Space Collapse • 23

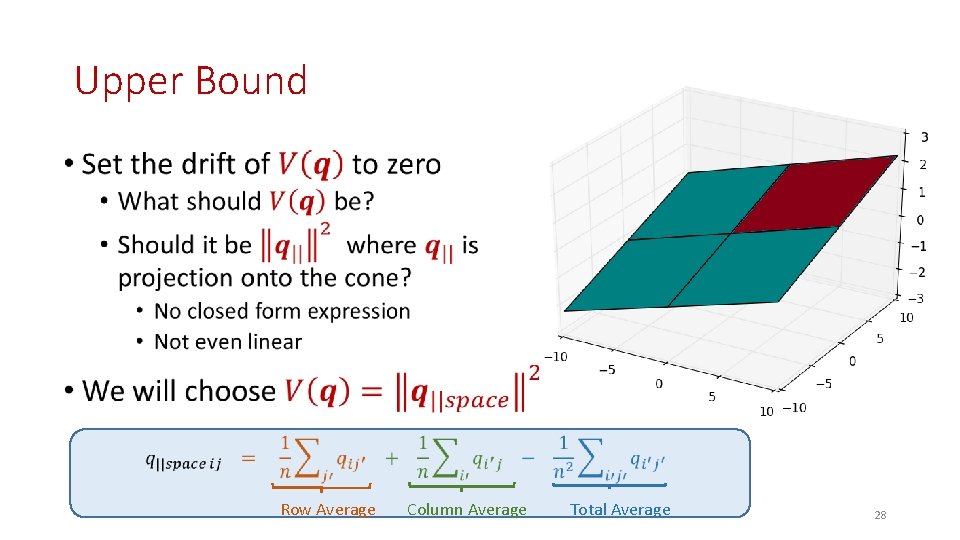
The Right Function for Upper bound • 24

Back to Max. Weight Scheduling in a Switch 25

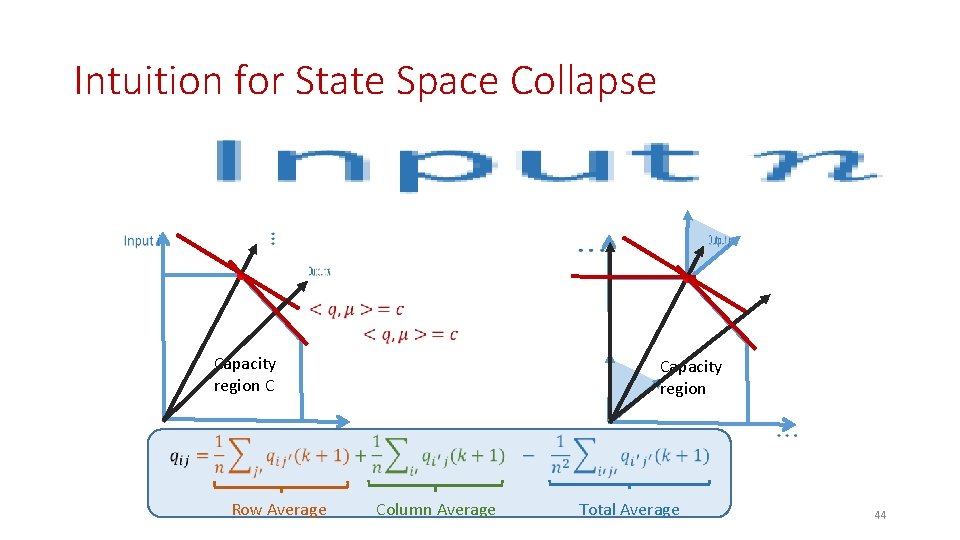
State Space Collapse • 26

State Space Collapse • Why? Under Max. Weight, queue lengths evolve so that all matchings have same weight. This cone is exact characterization of all such queue lengths Row Average Column Average Total Average 27

Upper Bound • Row Average Column Average Total Average 28

Asymptotically Tight Bounds • Sum of the queue lengths in column j Total queue length in the switch 29

Back to Main Result • Under Max. Weight 31

Interpretation of the Result • 32

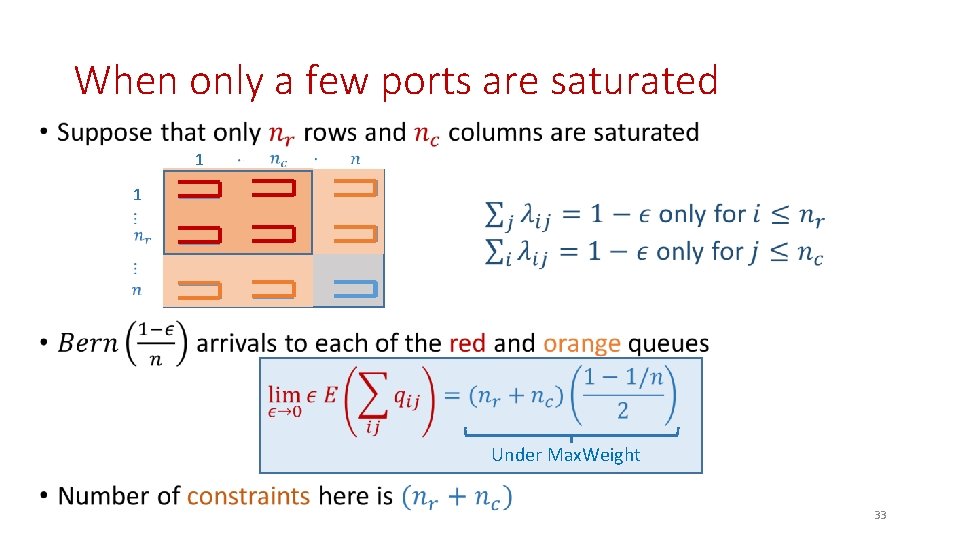
When only a few ports are saturated • 1 1 Under Max. Weight 33

Non-uniform saturation • 34

Joint Scaling of Traffic and Switch Size • 35

Open Question 1 • Universal Under Max. Weight 36

Open Question 2 • 37

Conclusions • 38

Backup slides 39

Why V(q)? • 40

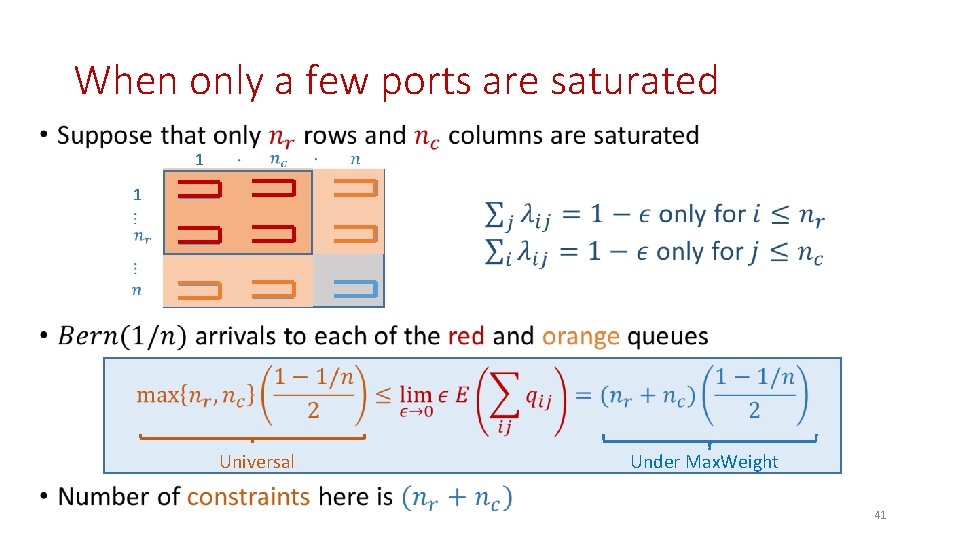
When only a few ports are saturated • 1 1 Universal Under Max. Weight 41

Max. Weight Algorithm • Capacity region C 43

Intuition for State Space Collapse • Capacity region C Capacity region Row Average Column Average Total Average 44

Kingman Bound • 45

Proof of State-Space Collapse • 46

Handling Cross-Terms • 47