Chapter 4 Quadratic Functions and Various Nonlinear Topics




























- Slides: 30

Chapter 4 Quadratic Functions and Various Nonlinear Topics Section 4. 1

Section 4. 1 Solving Quadratic Equations • Definition of Quadratic Equation • Methods of Solving Quadratic Equations: Ø Factoring Ø Square Root Method Ø Quadratic Formula and the Discriminant Ø Graphical Method • Modeling with Quadratic Equations: Ø Projectiles and Gravity Models Ø Other Models

Definition of Quadratic Equation A quadratic equation in x is a second-degree equation that has the standard form ax 2 + bx + c = 0 where a, b, and c are real numbers, a 0. a: leading coefficient b: coefficient of the first-degree term c: constant term

Solving Quadratic Equations by Factoring Zero Product Property: If a and b are real numbers, and ab = 0, then either a = 0, or b = 0, or both a and b are zero. Factoring Method: 1. Write the equation in standard form. (Make sure one side of the equation is 0. ) 2. Factor the nonzero side of the equation. 3. Apply the zero-product property. (Set each factor = 0. ) 4. Solve for the variable. 5. Verify your answers in the original equation.

Solve the quadratic equation x 2 – 9 x = – 14 by factoring. 1. Write the equation in standard form. x 2 – 9 x + 14 = 0 2. Factor the nonzero side of the equation. (x – 7)(x – 2) = 0 3. Apply the zero-product property. x – 7 = 0 or x – 2 = 0 4. Solve for the variable. x = 7 or x = 2 5. Verify your answers in the original equation.

Solve 1/7(245 x 2 + 7 x) = 12 by factoring. 1/7(245 x 2 + 7 x) = 12 35 x 2 + x – 12 = 0 (5 x + 3)(7 x – 4) = 0 5 x + 3 = 0 or 7 x – 4 = 0 x = – 3/5 or x = 4/7 Checking:

Following a major earthquake in a densely populated city, rescue helicopters released pallets of food, water, and needed supplies. One helicopter dropped supplies from a height of 256 feet. The height, h (in feet), of the first pallet after t seconds is modeled by h = – 16 t 2 + 256, where t ≥ 0. Solve the quadratic equation to determine when the first pallet reached the ground. The height of the pallet at ground level is 0 feet. Therefore, we can find the time it reached the ground by letting h = 0 and solving for t. – 16 t 2 + 256 = 0 – 16(t 2 – 16) = 0 t 2 – 16 = 0 (Divide both sides by – 16) (t – 4)(t + 4) = 0 t = 4 or t = – 4 Since time t ≥ 0 seconds, we discard t = – 4. The first pallet reached the ground at t = 4 seconds.

Solving by the Square Root Method: Useful method when b = 0 in ax 2 + bx + c = 0 (that is, no presence of the first-degree term, bx, in the standard form). Square Root Property: If x 2 = k, then x = or x = for k constant. Solutions of quadratic equations of the form x 2 = k are given by: x = (continued on the next slide)

Solving by the Square Root Method 1. Isolate the squared variable term. 2. Apply the square root property to undo the square. Remember to insert “ ” on the numeric side of the equation, since we want both the positive and negative square roots. 3. Simplify the radical expression. 4. Verify your answers in the original equation.

Solve 3 x 2 = 54 by the square root method. 1. Isolate the squared variable term: 2. Apply the square root property to undo the square. 3. Simplify the radical expression. 4. Solve for the variable. 5. Verify your answers in the original equation.

Solve by the square root method: 2(3 m – 6)2 – 29 = 43 2(3 m – 6)2 = 72 (3 m – 6)2 = 36 3 m – 6 = 6 3 m – 6 = 6 or 3 m – 6 = -6 m = 4 or m = 0 Checking:

An Application of Quadratic Equations: Compound Interest Account in which the interest is compounded annually. The interest is paid on the amount of money invested, and any interest earned from past years. Basic formula for compound interest: A = P(1 + r)n A = amount of money in the account P = principal (amount initially invested) n = number of years r = interest rate (expressed as a decimal value)

Blake wants to invest $6, 000 in an account that pays interest compounded annually. a. At the end of 2 years, how much money will Blake have in his account if the interest rate is 1. 75%? Round your answer to 2 decimal places. Let A = P(1 + r)n. We are looking for the value of A. A = amount of money in the account P = 6, 000 n = 2 r = 0. 0175 A = 6000(1 + 0. 0175)2 = 6000(1. 0275)2 = 6211. 84 At the end of 2 years, Blake will have $6, 211. 84.

(Contd. ) Blake wants to invest $6, 000 in an account that pays interest compounded annually. b. If Blake wants $6, 500 in this account after 2 years, what would the interest rate need to be? Approximate your answer to 2 decimal places. 6000(1 + r)2 = 6500 (1 + r) 2 = 1. 0833 1 + r = 1. 0408 – 1 r = – 2. 0408 or r = 0. 0408 The negative value makes no sense in the context of this problem, thus Blake would need an interest rate of 4. 08%.

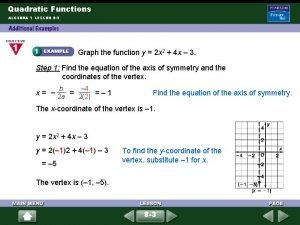
Quadratic Formula The solutions of a quadratic equation ax 2 + bx + c = 0, a 0, are given by where a is the coefficient of x 2, b is the coefficient of x, and c is the constant term of the quadratic equation.

Solve 2 x 2 – x – 6 = 0 by using the quadratic formula. First, we identify the values for a, b, and c: a = 2 b = – 1 c = – 6 Now we substitute these values into the quadratic formula and solve for x:

Solve x 2 + 3 x = 7 by using the quadratic formula. First, we rewrite the equation in standard form: x 2 + 3 x – 7 = 0 Using the quadratic formula with a = 1, b = 3, and c = – 7, we have: The exact solutions are given by: Decimal approximations: x 1. 5414 and x – 4. 5414

Quadratic Equations with Complex Solutions Solve x 2 – 4 x + 13 = 0 by using the quadratic formula. Using the quadratic formula with a = 1, b = – 4, and c = 13, we have: The solutions are:

The Discriminant How can we determine the nature of the solutions of a quadratic equation? The discriminant of a quadratic equation ax 2 + bx + c = 0, a 0, is given by b 2 – 4 ac. (Note: This expression is equivalent to the radicand in the quadratic formula. ) If b 2 – 4 ac > 0, the equation has two distinct real solutions. If b 2 – 4 ac = 0, the equation has one real solution. If b 2 – 4 ac < 0, the equation has no real solutions.

Use the discriminant, b 2 – 4 ac, to determine the number and type of solutions of each quadratic equation. a. x 2 + 3 x + 9 = 0 b. 5 x 2 = 12 c. x 2 – 18 x + 81 = 0 a. (3)2 – 4(1)(9) = 9 – 36 = – 27 No real solutions; two complex roots b. Rewrite the equation in standard form: 5 x 2 + 0 x – 12 = 0 (0)2 – 4(5)(– 12) = 240 Two distinct real solutions c. (– 18)2 – 4(1)(81) = 324 – 324 = 0 One real solution; a double root

Graphical Methods The solutions of a quadratic equation ax 2 + bx + c = 0, are the x-intercepts of the graph of the equation. If the graph has no x-intercepts, then the equation has no real solutions. Examples: Two distinct real solutions: One real solution: No real solution:

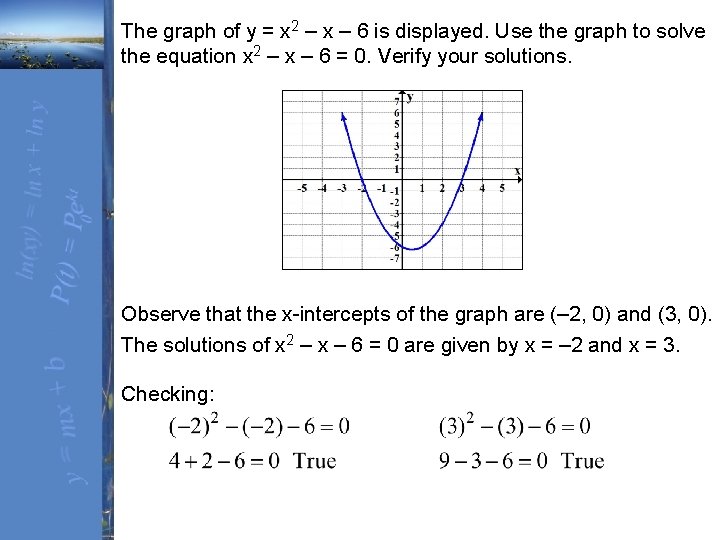
The graph of y = x 2 – x – 6 is displayed. Use the graph to solve the equation x 2 – x – 6 = 0. Verify your solutions. Observe that the x-intercepts of the graph are (– 2, 0) and (3, 0). The solutions of x 2 – x – 6 = 0 are given by x = – 2 and x = 3. Checking:

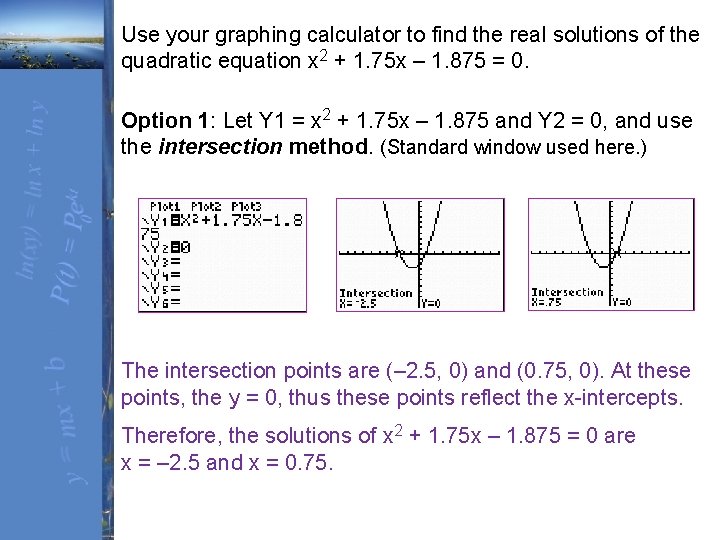
Use your graphing calculator to find the real solutions of the quadratic equation x 2 + 1. 75 x – 1. 875 = 0. Option 1: Let Y 1 = x 2 + 1. 75 x – 1. 875 and Y 2 = 0, and use the intersection method. (Standard window used here. ) The intersection points are (– 2. 5, 0) and (0. 75, 0). At these points, the y = 0, thus these points reflect the x-intercepts. Therefore, the solutions of x 2 + 1. 75 x – 1. 875 = 0 are x = – 2. 5 and x = 0. 75.

(Contd. ) Use your graphing calculator to find the real solutions of the quadratic equation x 2 + 1. 75 x – 1. 875 = 0. Option 2: Let Y 1 = x 2 + 1. 75 x – 1. 875 and use the intercepts (zero) method. (Standard window used here. ) The x-intercepts (zeros) of the graph are (– 2. 5, 0) and (0. 75, 0). Therefore, the solutions of x 2 + 1. 75 x – 1. 875 = 0 are x = – 2. 5 and x = 0. 75.

Projectiles and Gravity Models As an object is launched into the air, gravity will force it down. Ignoring any other forces acting upon the launched object, we can use the following formulas to represent its height, h. Height measured in feet: h = – 16 t 2 + v 0 t + h 0. Initial velocity of v 0 feet per second from an initial height of h 0 feet above the ground, after t seconds. Height measured in meters: h = – 4. 9 t 2 + v 0 t + h 0. Initial velocity of v 0 meters per second from an initial height of h 0 meters above the ground, after t seconds.

During a New Year's Eve celebration, fireworks were launched from a platform 7 feet high with an initial velocity of 111 feet per second. a. Write a quadratic equation that models the height in feet, h, of the fireworks at t seconds. We can use the formula h = – 16 t 2 + v 0 t + h 0 with v 0 = 111 ft/s and h 0 = 7. h = – 16 t 2 + 111 t + 7 b. Find the height of the fireworks after 2 seconds. Evaluating the height formula for t = 2, we have: h = – 16(2)2 + 111(2) + 7 = 165 feet

(Contd. ) c. When did the first remnants of the fireworks reach the ground? We know h = – 16 t 2 + 111 t + 7. Let h = 0 (ground level) and solve the quadratic equation – 16 t 2 + 111 t + 7 = 0 for t. 16 t 2 – 111 t – 7 = 0 (Divide both sides by – 1) (16 t + 1)(t – 7) = 0 16 t + 1 = 0 or t – 7 = 0 t = – 1/16 or t = 7 A negative time-value makes no sense in the context of this problem. The first remnants of the fireworks reached the ground at t = 7 seconds.

(Contd. ) d. At what time did the fireworks reach a height of 102 feet on their way up? We let h =102 and solve – 16 t 2 + 111 t + 7 = 102 for t. – 16 t 2 + 111 t – 95 = 0 16 t 2 – 111 t + 95 = 0 (16 t – 95)(t – 1) = 0 16 t – 95 = 0 or t – 1 = 0 t = 95/16 5. 9375 or t = 1 The fireworks reached a height of 102 feet on their way up after 1 second. (Note that t = 5. 9375 would represent the seconds on the way down. )

(Contd. ) During a New Year's Eve celebration, fireworks were launched from a platform 7 feet high with an initial velocity of 111 feet per second. We can also use a graphical method to answer the question on part d: At what time did the fireworks reach a height of 102 feet on their way up? The fireworks reached a height of 102 feet on their way up after 1 second.

Using your textbook, practice the problems assigned by your instructor to review the concepts from Section 4. 1.
 Is quadratic equation nonlinear
Is quadratic equation nonlinear Non linear table
Non linear table Patterns and nonlinear functions
Patterns and nonlinear functions Chapter 9 quadratic equations and functions
Chapter 9 quadratic equations and functions Chapter 8 quadratic functions and equations answer key
Chapter 8 quadratic functions and equations answer key Chapter 6 quadratic functions and inequalities answers
Chapter 6 quadratic functions and inequalities answers Chapter 3 linear and quadratic functions
Chapter 3 linear and quadratic functions Chapter 1 quadratic functions and factoring answers
Chapter 1 quadratic functions and factoring answers Factors affecting span of control
Factors affecting span of control Lesson 8 extra practice quadratic functions
Lesson 8 extra practice quadratic functions Modeling with quadratic functions
Modeling with quadratic functions Elimination quadratic equation
Elimination quadratic equation Quadratic formula
Quadratic formula Crime scene factoring and quadratic functions answer key
Crime scene factoring and quadratic functions answer key Linear exponential and quadratic functions
Linear exponential and quadratic functions Maximum and minimum values of quadratic functions
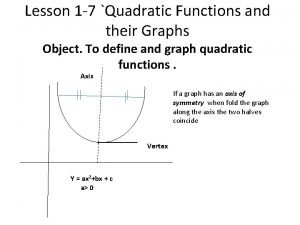
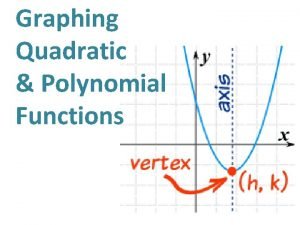
Maximum and minimum values of quadratic functions Quadratic functions and their graphs
Quadratic functions and their graphs Crime scene factoring and quadratic functions answer key
Crime scene factoring and quadratic functions answer key Function in standard form
Function in standard form Graph opens up or down
Graph opens up or down Relative vs absolute max and min
Relative vs absolute max and min Domain of a parabola
Domain of a parabola Solving graphing and analyzing quadratic functions
Solving graphing and analyzing quadratic functions 4-1 quadratic functions and transformations
4-1 quadratic functions and transformations Quadratic functions: vertex form assignment
Quadratic functions: vertex form assignment Intercept form
Intercept form Quadratic transformations quiz
Quadratic transformations quiz Facts about quadratic functions
Facts about quadratic functions Introduction to quadratic function
Introduction to quadratic function Suppose a particular star is projected from a firework
Suppose a particular star is projected from a firework Quadratic formula vocabulary words
Quadratic formula vocabulary words