Chapter 4 Quadratic Functions and Various Nonlinear Topics

Chapter 4 Quadratic Functions and Various Nonlinear Topics Section 4. 3

Section 4. 3 Quadratic Inequalities • Solving a Quadratic Inequality by Graphing • Applications

Definition of Quadratic Inequality A quadratic inequality in one variable is an inequality which can be written in the form ax 2 + bx + c > 0 where a, b, and c are real numbers, a 0. The > symbol may be replaced with < , , or .

Solving a Quadratic Inequality by Graphing Recall that the solutions of a quadratic equation ax 2 + bx + c = 0 occur at the zeros or x-intercepts of the graph. We can solve a quadratic inequality by examining the graph of the associated function f(x) = ax 2 + bx + c, and finding the intervals where the function is above, on, or below the x-axis (that is, above, on, or below y = 0). We make sure that one side of the quadratic inequality is equal to zero. We graph the inequality to determine where the graph is above, on, or below the x-axis.

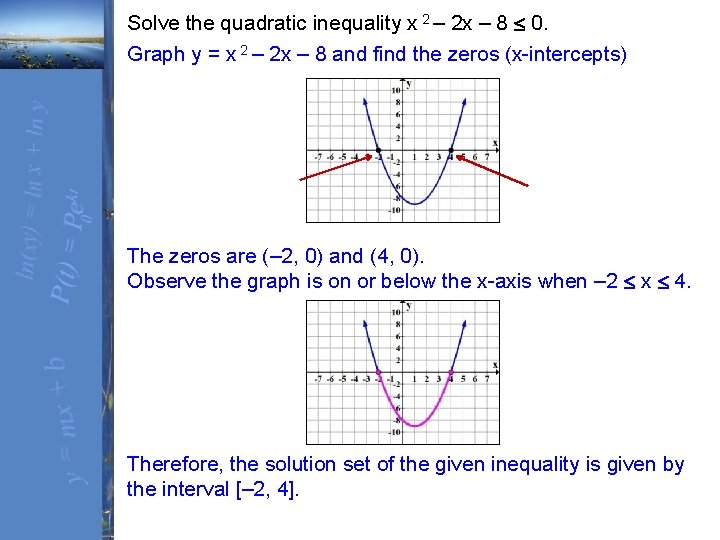
Solve the quadratic inequality x 2 – 2 x – 8 0. Graph y = x 2 – 2 x – 8 and find the zeros (x-intercepts) The zeros are (– 2, 0) and (4, 0). Observe the graph is on or below the x-axis when – 2 x 4. Therefore, the solution set of the given inequality is given by the interval [– 2, 4].

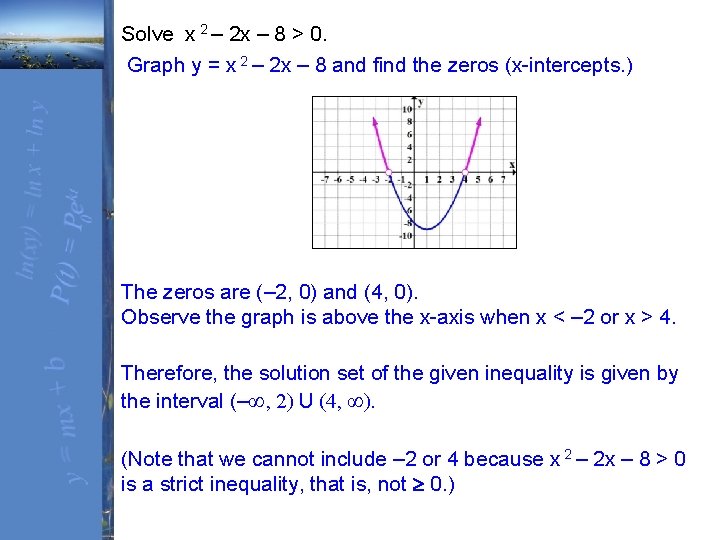
Solve x 2 – 2 x – 8 > 0. Graph y = x 2 – 2 x – 8 and find the zeros (x-intercepts. ) The zeros are (– 2, 0) and (4, 0). Observe the graph is above the x-axis when x < – 2 or x > 4. Therefore, the solution set of the given inequality is given by the interval (–∞, 2) U (4, ∞). (Note that we cannot include – 2 or 4 because x 2 – 2 x – 8 > 0 is a strict inequality, that is, not 0. )

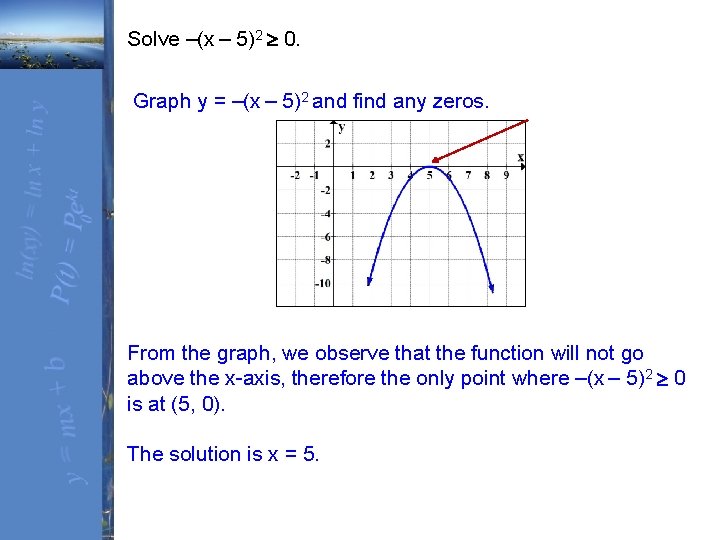
Solve –(x – 5)2 0. Graph y = –(x – 5)2 and find any zeros. From the graph, we observe that the function will not go above the x-axis, therefore the only point where –(x – 5)2 0 is at (5, 0). The solution is x = 5.

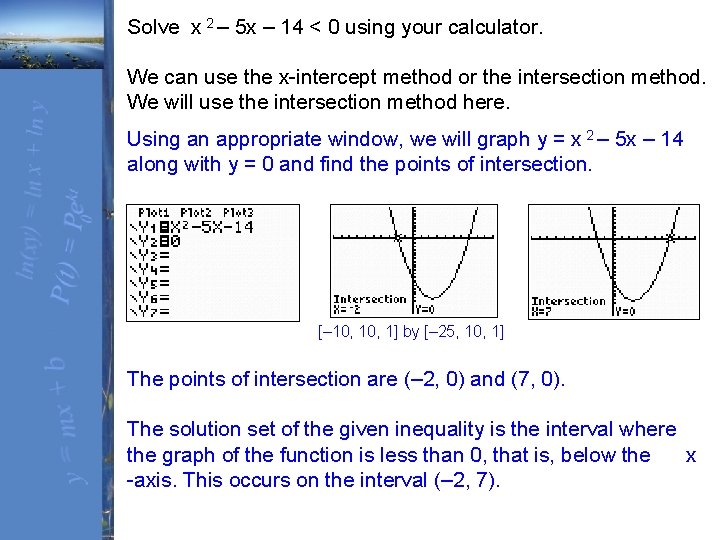
Solve x 2 – 5 x – 14 < 0 using your calculator. We can use the x-intercept method or the intersection method. We will use the intersection method here. Using an appropriate window, we will graph y = x 2 – 5 x – 14 along with y = 0 and find the points of intersection. [– 10, 1] by [– 25, 10, 1] The points of intersection are (– 2, 0) and (7, 0). The solution set of the given inequality is the interval where the graph of the function is less than 0, that is, below the x -axis. This occurs on the interval (– 2, 7).

A company sells 1550. 5 – 25 x sports memorabilia baskets each season, and they charge x dollars per basket. The company wants the revenue from the baskets to be at least $8, 200 per season. Use your graphing calculator with a window of [0, 80, 20] by [0, 18000, 1000] to answer the following question a. What is the revenue function which models this problem? Recall that revenue R(x) = price quantity. The function that models this problem is given by R(x) = (x)(1550. 5 – 25 x) or R(x) = 1550. 5 x – 25 x 2. (continued on the next slide)

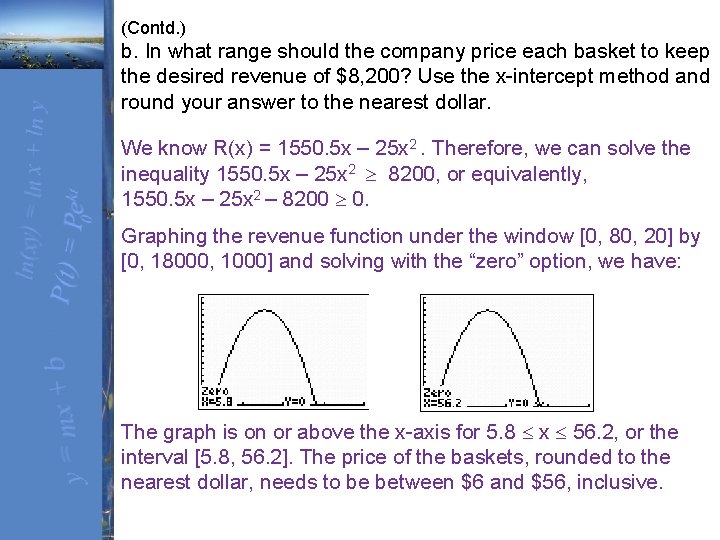
(Contd. ) b. In what range should the company price each basket to keep the desired revenue of $8, 200? Use the x-intercept method and round your answer to the nearest dollar. We know R(x) = 1550. 5 x – 25 x 2. Therefore, we can solve the inequality 1550. 5 x – 25 x 2 8200, or equivalently, 1550. 5 x – 25 x 2 – 8200 0. Graphing the revenue function under the window [0, 80, 20] by [0, 18000, 1000] and solving with the “zero” option, we have: The graph is on or above the x-axis for 5. 8 x 56. 2, or the interval [5. 8, 56. 2]. The price of the baskets, rounded to the nearest dollar, needs to be between $6 and $56, inclusive.

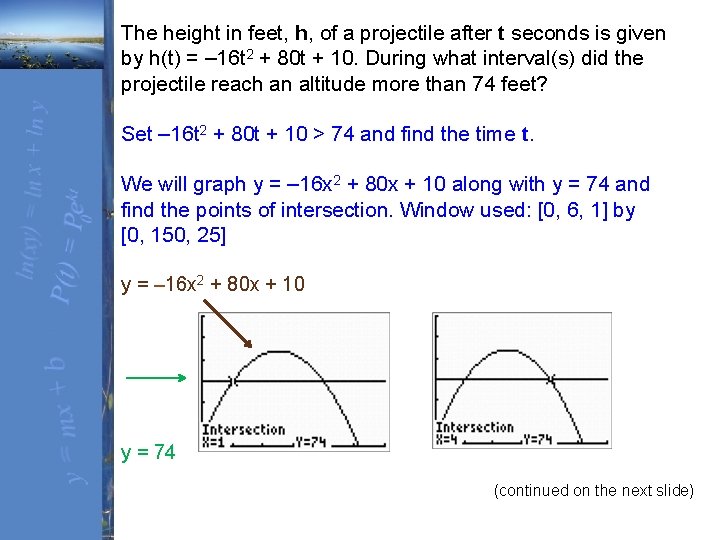
The height in feet, h, of a projectile after t seconds is given by h(t) = – 16 t 2 + 80 t + 10. During what interval(s) did the projectile reach an altitude more than 74 feet? Set – 16 t 2 + 80 t + 10 > 74 and find the time t. We will graph y = – 16 x 2 + 80 x + 10 along with y = 74 and find the points of intersection. Window used: [0, 6, 1] by [0, 150, 25] y = – 16 x 2 + 80 x + 10 y = 74 (continued on the next slide)

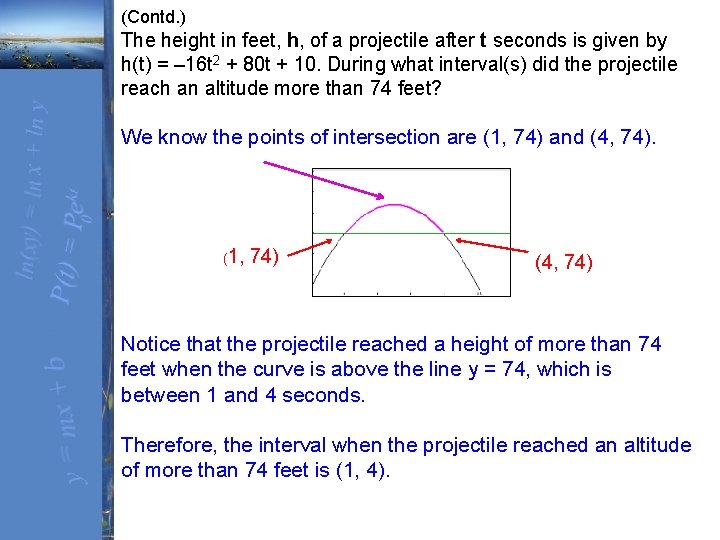
(Contd. ) The height in feet, h, of a projectile after t seconds is given by h(t) = – 16 t 2 + 80 t + 10. During what interval(s) did the projectile reach an altitude more than 74 feet? We know the points of intersection are (1, 74) and (4, 74). (1, 74) (4, 74) Notice that the projectile reached a height of more than 74 feet when the curve is above the line y = 74, which is between 1 and 4 seconds. Therefore, the interval when the projectile reached an altitude of more than 74 feet is (1, 4).

Using your textbook, practice the problems assigned by your instructor to review the concepts from Section 4. 3.