CAP 1 Soluo de Sistemas Lineares MCC 03

CAP 1 – Solução de Sistemas Lineares MCC 03 – MATEMÁTICA APLICADA 2º Semestre de 2017 CAPÍTULO I ÁLGEBRA LINEAR – SOLUÇÃO DE SISTEMAS LINEARES Prof. Sebastião Simões C. Jr Prof. Marcelo Santiago de Sousa UNIFEI – Universidade Federal de Itajubá IEM – Instituto de Engenharia Mecânica

CAP 1 – Solução de Sistemas Lineares 1. 0. Conteúdo Cap. 1 – Álgebra Linear – Solução de Sistemas Lineares 1) Sistemas Lineares 1. 1) Métodos Diretos (aula 1) Decomposição de: Crout, Doolittle, Cholesky e Gauss (aula 1); 1. 2) Resolução de Sistemas Triangulares (aula 2) 1. 3) Implementação Computacional Armazenamento Vetorial para Matrizes Triangulares (aula 2) Armazenamento Vetorial para Sistemas Esparsos 1. 4) Solução de Sistemas Lineares Eliminação de Gauss (aula 3) 1. 5) Sistemas Lineares Sub-Determinados (aula 3); 1. 6) Sistemas Lineares Super-Determinados (aula 3); 1. 7) Sistemas Lineares Homogêneos (aula 3);

CAP 1 – Solução de Sistemas Lineares 1. 0. Conteúdo Cap. 2 – Álgebra Linear – Vetores e Matrizes 2. 1) Vetores 2. 2) Ortogonalização de Gram-Schmidt 2. 3) Matrizes 2. 4) Autovalores e Autovetores Cap. 3 – Problemas de Autovalores e Autovetores 3. 1) Número de Condição; 3. 2) Translação de Autovalores; 3. 3) Teorema de Gerschgorin; 3. 4) Método da Potência; 3. 5) Método da Iteração Inversa; 3. 6) Transformação Similar; 3. 7) Método de Jacobi; 3. 8) Transformação de Householder; 3. 9) Decomposição QR

CAP 1 – Solução de Sistemas Lineares 1. 0. Conteúdo Cap. 4 – Tópicos sobre Otimização 4. 1) Otimização Irrestrita 4. 2) Método de Newton-Raphson 4. 3) Método de Newton 4. 4) Método Quase Newton :

CAP 1 – Solução de Sistemas Lineares Avaliação • Prova teórica; • Apresentação de trabalhos práticos; :

CAP 1 – Solução de Sistemas Lineares 1. 0. Introdução Muitos problemas em engenharia tem solução que exigem complexos cálculos para resolução; Muitos problemas em engenharia podem ser modelados como equações algébricas (lineares), equações diferencias lineares/ não lineares, etc; O uso de computadores permite resolução mais rápida dos cálculos; Hoje em dia já há muitas ferramentas de cálculo que permitem a solução rápida das equações; Contudo, é importante que os engenheiros tenham um entendimento do que o computador está fazendo; Esta é uma motivação para que alunos de pós-graduação tenham um curso de matemática aplicada (cálculo numérico);

CAP 1 – Solução de Sistemas Lineares 1. 0. Introdução Computadores podem adicionar erros de arredondamento e/ou de truncamento, que podem tornar a solução não exata; Métodos eficientes de cálculo numérico podem ajudar a obtenção de respostas exatas; O conhecimento de métodos eficientes podem ajudar alunos na obtenção de soluções mais precisas; Alunos de pós-graduação do IEM farão teses/pesquisas em diferentes disciplinas onde eles deverão usar métodos numéricos para a obtenção de soluções (mecânica dos fluidos, máquinas de fluxo, processos de fabricação, materiais, vibrações mecânicas, etc); O curso xxxx visa reforçar alguns conceitos já aprendidos na graduação em engenharia e capacitar mais os alunos no uso de métodos numéricos.

CAP 1 – Solução de Sistemas Lineares 1. Sistemas de Equações Lineares Considere o sistema linear abaixo com m equações e n incógnitas: a 11 x 1 + a 12 x 2 +. . . + a 1 nxn = b 1 a 21 x 1 + a 22 x 2 +. . . + a 2 nxn = b 2. . . am 1 x 1 + am 2 x 2 +. . . + amnxn = bm (1) A solução do sistema é uma n-upla {x 1 x 2. . . xn} que satisfaça simultaneamente as m equações.

CAP 1 – Solução de Sistemas Lineares Escrevendo na forma matricial tem-se: a 11 a 12. . . a 1 n a 21 a 22. . . a 2 n. . . am 1 am 2. . . amn x 1 x 2. . . xm = b 1 b 2. . . bm (2) [A]mxn {x}nx 1 = {b}mx 1 onde: [A]: matriz de coeficientes {x}: vetor de incógnitas {b}: vetor de termos independentes O sistema é chamado de homogêneo se {b} ={0}. Caso contrário, é chamado de não-homogêneo.

CAP 1 – Solução de Sistemas Lineares Caso m = n, tem-se um sistema quadrado. Neste caso: [A]nxn{x}nx 1 = {b}nx 1 [A]{x} = {b} [A]-1[A]{x} = [A]-1{b} [ I ]{x} = [A]-1{b}

CAP 1 – Solução de Sistemas Lineares 1. 1. Métodos Diretos – Fatorização em LU Métodos Diretos são aqueles que conduzem à solução exata a menos de erros de arredondamento introduzidos pela máquina, após um número finito de passos. Considere um sistema de equações lineares nxn com n variáveis: [A]nxn{x}nx 1 = {b}nx 1 Três métodos: “DOOLITTLE”, “CROUT” e “CHOLESKY” podem ser utilizados para resolver tais sistemas. Eles usam a ideia da Fatorização-LU de [A]. A Fatorização-LU de uma matriz quadrada [A] é da forma: [A] = [L][U] [L]: Matriz triangular inferior. [U]: Matriz triangular superior. (3)

CAP 1 – Solução de Sistemas Lineares Considere o sistema abaixo: A Fatorização-LU é única.

CAP 1 – Solução de Sistemas Lineares 1. 2. Matriz [A] não simétrica: [A] ≠ [A]T 1. 2. 1. Método de DOOLITTLE (4 a) (4 b) - A solução é obtida resolvendo (4 a) para {y} e (4 b) para {x}. - [L] possui diagonal principal igual a unidade.

CAP 1 – Solução de Sistemas Lineares 1. 2. 2. Método de CROUT Este método é obtido a partir de (3) se [U] tiver diagonal principal igual à unidade. Em ambos os casos, a Fatorização-LU é única.

CAP 1 – Solução de Sistemas Lineares EXEMPLO: Resolva o sistema usando os métodos de DOOLITTLE e CROUT: DOOLITTLE

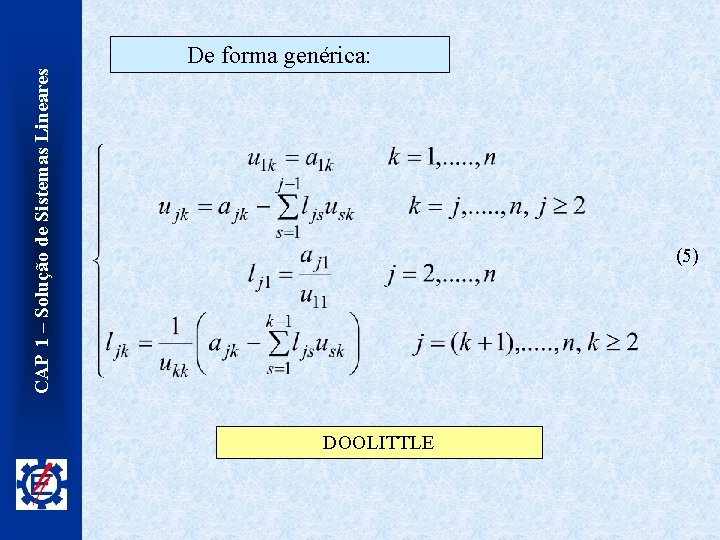
CAP 1 – Solução de Sistemas Lineares De forma genérica: (5) DOOLITTLE

CAP 1 – Solução de Sistemas Lineares De forma genérica: (6) CROUT

CAP 1 – Solução de Sistemas Lineares 1. 3. Matriz [A] simétrica: [A] = [A]T 1. 3. 1. Método de CHOLESKY Simétrica, definida positiva Sem nenhuma condição sobre os valores da diagonal principal.

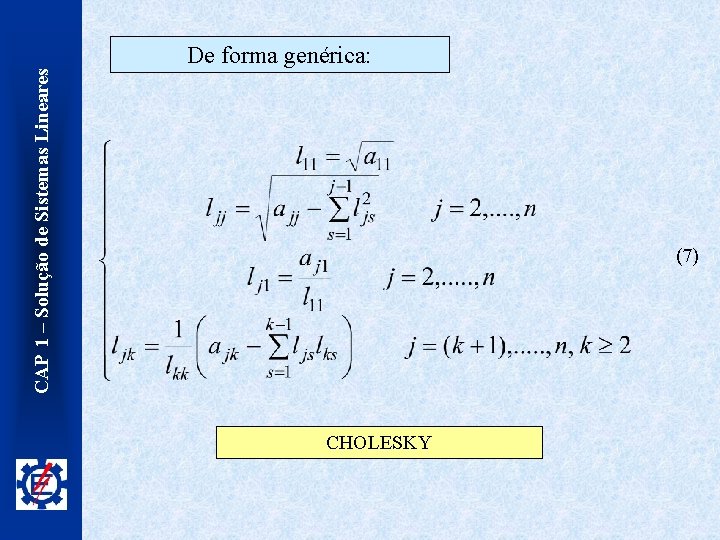
CAP 1 – Solução de Sistemas Lineares De forma genérica: (7) CHOLESKY

CAP 1 – Solução de Sistemas Lineares EXEMPLO: Resolva o sistema de equações usando o método de CHOLESKY:

CAP 1 – Solução de Sistemas Lineares 1. 3. 2. Método de GAUSS (8) Onde: [U]: tem a diagonal principal igual a 1. [D]: matriz diagonal.

CAP 1 – Solução de Sistemas Lineares Tem-se: Fazendo: Pré-multiplicando por [D]-1 (9) Assim: onde: (10) (11) Resolve-se o sistema triangular inferior (11), encontrando {y}. A seguir, determina-se (10) e encontra-se {x} a partir de (9).

CAP 1 – Solução de Sistemas Lineares 1. 4. Resolução de Sistemas Triangulares 1. 4. 1. Triangular Inferior

CAP 1 – Solução de Sistemas Lineares Fazendo a multiplicação matricial tem-se: Generalizando:

CAP 1 – Solução de Sistemas Lineares 1. 4. 2. Triangular Superior

CAP 1 – Solução de Sistemas Lineares Fazendo a multiplicação matricial tem-se: Generalizando:

CAP 1 – Solução de Sistemas Lineares Algoritmo – Triangular Inferior - entre com os valores de [L] e {b} - y 1 = b 1/l 11 - repita para i = 2 até n soma = 0 repita para j = 1 até (i-1) soma = soma + lij · yj fim yi = (bi – soma) / lii fim - Mostrar yi Exemplo:

CAP 1 – Solução de Sistemas Lineares 1. 5. Eliminação de Gauss É um método para resolução de sistemas de equações lineares (1), no qual o sistema é reduzido a uma forma triangular. Como exemplo de uma forma triangular têm-se Resolvendo o sistema, na substituição de valores têm-se Considere o sistema O sistema será transformado em um sistema triangular superior se: (1)

CAP 1 – Solução de Sistemas Lineares 1. 6. Implementação Computacional 1. 6. 1. Armazenamento vetorial de matrizes triangulares Dado uma matriz triangular superior Pode-se armazená-la em um vetor da forma Ou,

CAP 1 – Solução de Sistemas Lineares Para relacionar os elementos da matriz [U] com os elementos do vetor {u}, deve-se usar a seguinte fórmula de relação triangular superior posição do vetor Se [U] for triangular inferior posição do vetor

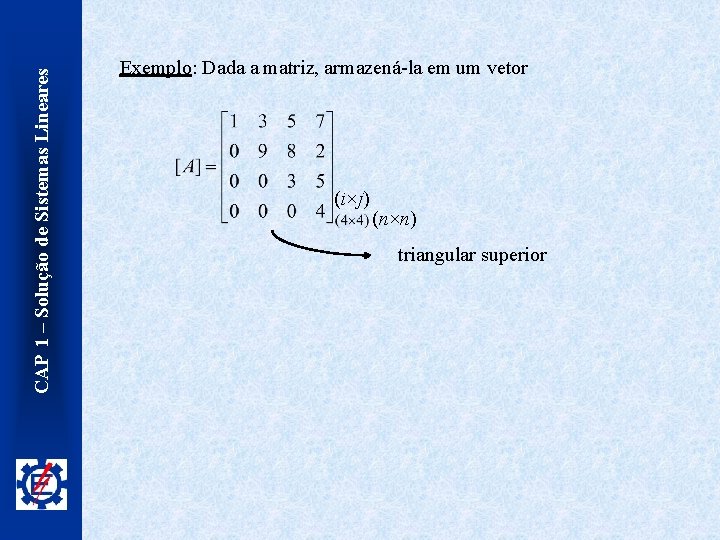
CAP 1 – Solução de Sistemas Lineares Exemplo: Dada a matriz, armazená-la em um vetor (i×j) (n×n) triangular superior

CAP 1 – Solução de Sistemas Lineares 1. 7. Sistemas Lineares Sub-Determinados Seja o sistema linear retangular onde m<n A solução {x} é obtida fazendo 1) Aplicar a Eliminação de Gauss 2) Verificar a consistência do sistema triangular superior Assim, obtêm-se [0] Onde, B – variáveis básicas L – variáveis livres

CAP 1 – Solução de Sistemas Lineares Desta forma, a matriz [A] resulta Caso , o sistema é dito consistente e o sistema possui solução que não será única. Assim, pré-multiplicando por

CAP 1 – Solução de Sistemas Lineares 1. 8. Sistemas Lineares Super-Determinados Considere o sistema de equações onde, Usando a solução de mínimos quadrados Exemplo: Resolva o sistema m>n

CAP 1 – Solução de Sistemas Lineares 1. 9. Sistemas Lineares Homogêneos Considere o sistema de equações Caso têm-se um sistema homogêneo Aplicando a Eliminação de Gauss, têm-se: Resolvendo

MCC 03 – MATEMÁTICA APLICADA CAP 2 – Vetores e Matrizes 1º Semestre de 2013 CAPÍTULO II ÁLGEBRA LINEAR – VETORES E MATRIZES Prof. Sebastião Simões C. Jr sebas@unifei. edu. br UNIFEI – Universidade Federal de Itajubá IEM – Instituto de Engenharia Mecânica

2. 1. Vetores CAP 2 – Vetores e Matrizes Um vetor é uma matriz com somente uma linha ou uma coluna: - VETORES UNITARIOS

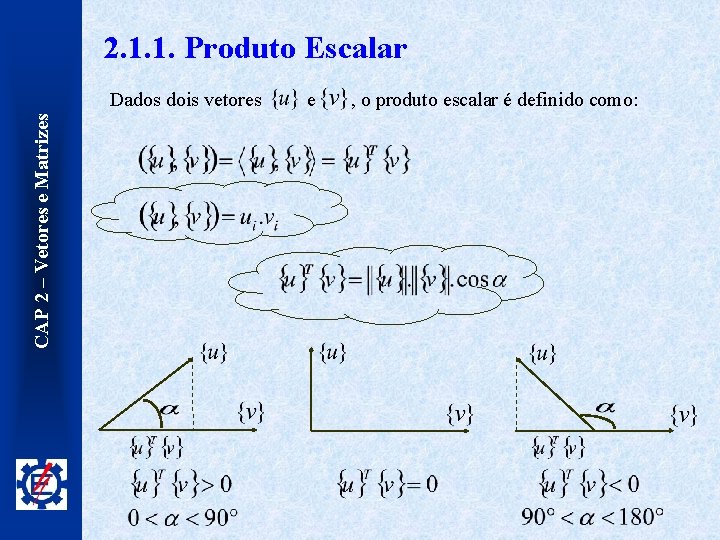
2. 1. 1. Produto Escalar CAP 2 – Vetores e Matrizes Dados dois vetores e , o produto escalar é definido como:

CAP 2 – Vetores e Matrizes Exemplo: Aplicação: - O vetor Exemplo: é unitário Projeção de direção de na

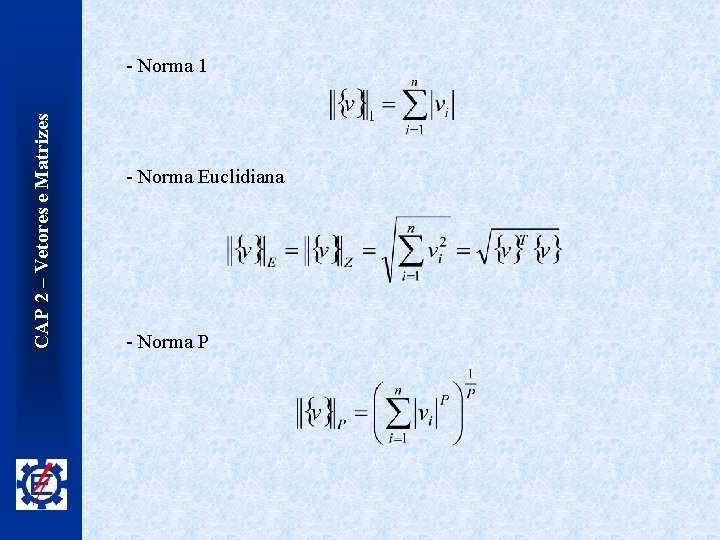
CAP 2 – Vetores e Matrizes 2. 1. 2. Norma de um Vetor A norma de um vetor as propriedades: , de ordem n, é um numero real que satisfaz 1) 2) 3) Exemplo de normas: - Norma máxima ou norma finita

CAP 2 – Vetores e Matrizes - Norma 1 - Norma Euclidiana - Norma P

CAP 2 – Vetores e Matrizes 2. 1. 3. Conjuntos Ortogonais e Ortonormais de Vetores Um conjunto de vetores é ortogonal, se: Para Se além disto, os vetores igual a 1), isto é: porem unitários (norma Para O conjunto é chamado ortonormal. Exemplo:

CAP 2 – Vetores e Matrizes 2. 2. Ortogonalização de GRAM-SCHMIDT Qualquer conjunto de vetores independentes Podem ser convertidos em um conjunto de vetores ortogonais tais que: Usando a “ortogonalização de gram-schmidt”

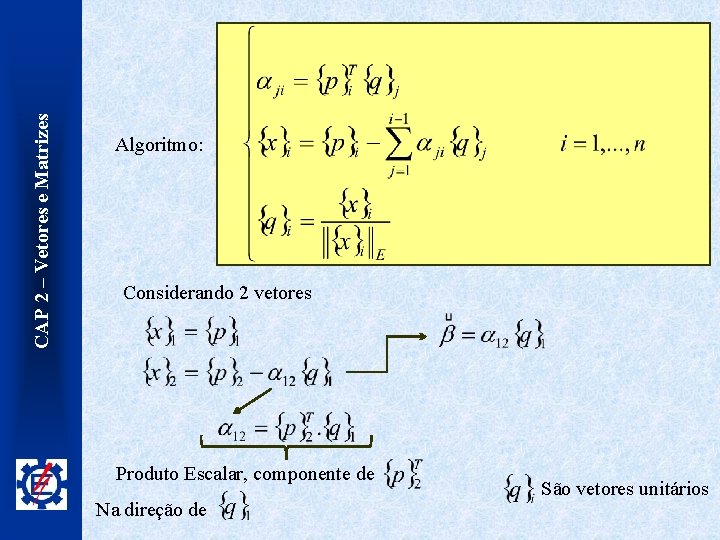
CAP 2 – Vetores e Matrizes Algoritmo: Considerando 2 vetores Produto Escalar, componente de Na direção de São vetores unitários

Exemplo: CAP 2 – Vetores e Matrizes Dado os vetores: Encontrar as bases ortonormais Usando gram-schmidt OLHOO!!! ENTRE AS PAGINAS 7 E 8 NÃO VEJO SEQUENCIA ALGUMA

Visualização do problema anterior CAP 2 – Vetores e Matrizes (Geogebra)

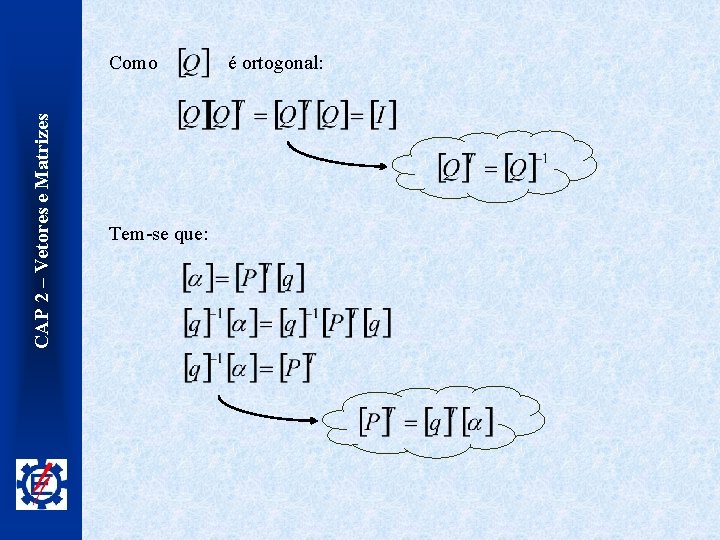
CAP 2 – Vetores e Matrizes Como Tem-se que: é ortogonal:

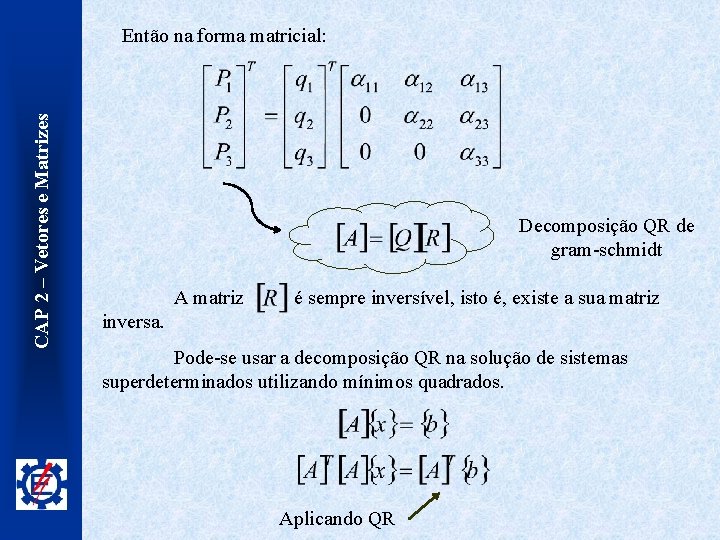
CAP 2 – Vetores e Matrizes Então na forma matricial: Decomposição QR de gram-schmidt A matriz é sempre inversível, isto é, existe a sua matriz inversa. Pode-se usar a decomposição QR na solução de sistemas superdeterminados utilizando mínimos quadrados. Aplicando QR

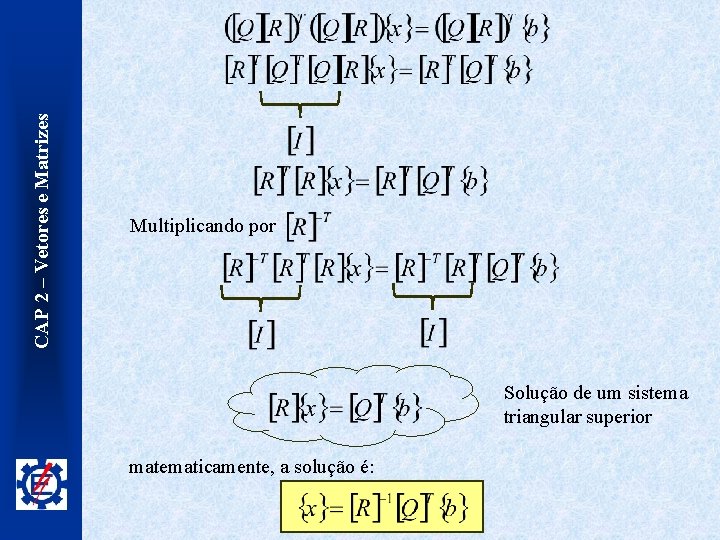
CAP 2 – Vetores e Matrizes Multiplicando por Solução de um sistema triangular superior matematicamente, a solução é:

CAP 2 – Vetores e Matrizes 2. 3. MATRIZES a) Matriz Diagonal: É uma matriz quadrada com elementos iguais a zero fora da diagonal principal. Para

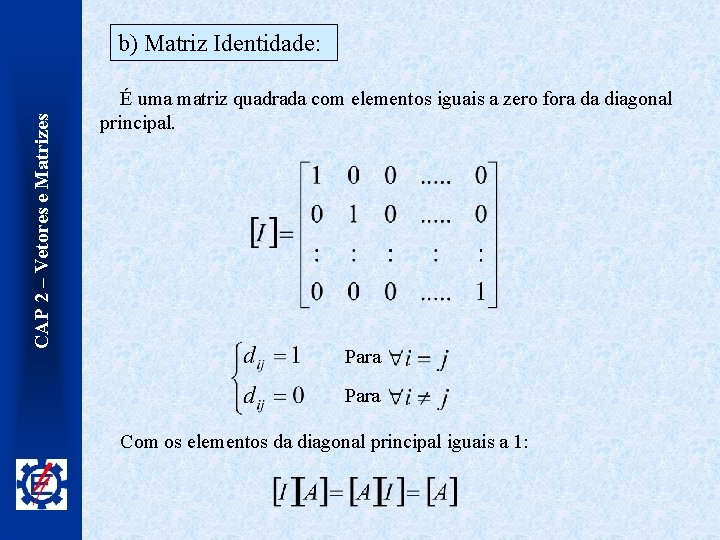
CAP 2 – Vetores e Matrizes b) Matriz Identidade: É uma matriz quadrada com elementos iguais a zero fora da diagonal principal. Para Com os elementos da diagonal principal iguais a 1:

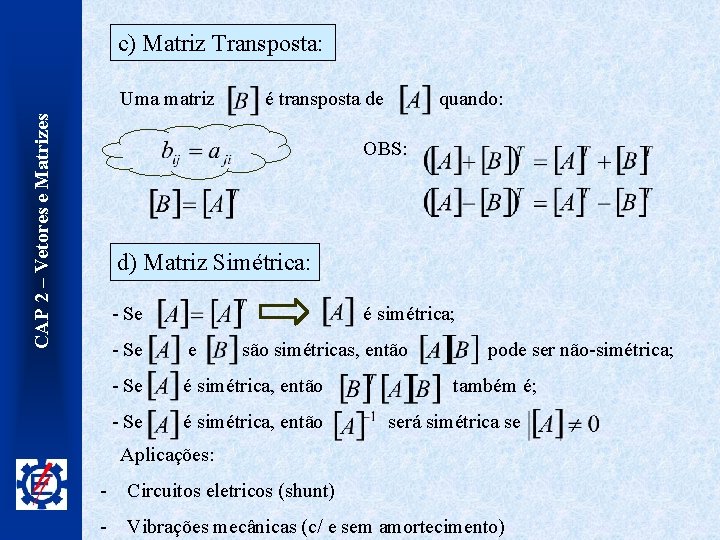
c) Matriz Transposta: CAP 2 – Vetores e Matrizes Uma matriz é transposta de quando: OBS: d) Matriz Simétrica: - Se é simétrica; - Se e são simétricas, então - Se é simétrica, então pode ser não-simétrica; também é; será simétrica se Aplicações: - Circuitos eletricos (shunt) - Vibrações mecânicas (c/ e sem amortecimento)

CAP 2 – Vetores e Matrizes e) Matriz Anti-Simétrica: c. q. d f) Matrizes Positivas Definidas: - Se para positiva definida - Se para positiva semi-definida

CAP 2 – Vetores e Matrizes g) Matriz Complexa: Onde e são reais h) Matriz Conjugada Complexa: i) Matriz Inversa: Onde e matriz inversa de

CAP 2 – Vetores e Matrizes OBS: A matriz inversa é única e são inversas de . Assim: Logo: é a inversa de é única.

CAP 2 – Vetores e Matrizes i. 1. Cálculo da Inversa Usando o Método de Gauss-Jordan - Dado a) Eliminação de Gauss de b) c) Exemplo:

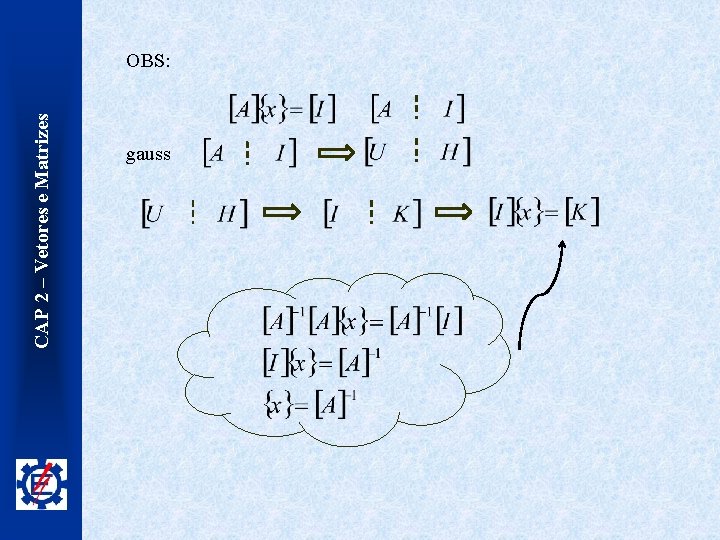
CAP 2 – Vetores e Matrizes OBS: gauss

CAP 2 – Vetores e Matrizes j) Classe, Posto ou Rank de uma Matriz O rank de uma matriz independentes de é o número máximo de linhas linearmente Exemplo: k) Cofator de [A] Onde Exemplo: é o determinante menos a linha i e a coluna j Calcule

CAP 2 – Vetores e Matrizes l) Matriz de Cofatores [Ā] m) Matriz Adjunta de [A]

CAP 2 – Vetores e Matrizes n) Determinante de uma Matriz Quadrada Exemplo: Calcule

CAP 2 – Vetores e Matrizes Propriedades dos Determinantes 1) 2) 3) 4) 5) n é a ordem da matriz 6) Troca de duas linhas ou colunas muda o sinal do determinante. 7) Se e são matrizes triangulares:

CAP 2 – Vetores e Matrizes OBS: dada uma matriz A matriz Se existe se e somente se: é chamada de singular se é não-singular

CAP 2 – Vetores e Matrizes OBS: fórmulas úteis para inversas: desde que: OBS: matrizes diagonais: A matriz somente se todos tem uma inversa, se e é diagonal com valores Exemplo: Calcule resposta

CAP 2 – Vetores e Matrizes

CAP 2 – Vetores e Matrizes

CAP 2 – Vetores e Matrizes

CAP 2 – Vetores e Matrizes

CAP 2 – Vetores e Matrizes

CAP 2 – Vetores e Matrizes