Sistemas de equaes lineares MCEF 201112 Sistemas Lineares

Sistemas de equações lineares MCEF 2011/12

Sistemas Lineares O Sistemas lineares constituem um caso particular dos sistemas não lineares, sendo que os métodos estudados se aplicam também a estes. Chamamos sistema de equações lineares a qualquer sistema do tipo:

Forma matricial Os sistemas lineares podem ser escritos na sua forma matricial, tendo em conta a definição da operações de multiplicação de matrizes.

Métodos Iterativos para sistemas lineares (um exemplo) Vamos tentar resolver o um sistema linear utilizando o método do ponto fixo. Para tal devemos reescrever o sistema na forma x = G(x), o que equivale a, em cada equação, isolar a respectiva variável. Uma forma de o fazer pode ser a seguinte:

Método de Jacobi O Processo descrito anteriormente conduz a um método conhecido como Método de Jacobi, que pode ser descrito pelo seguinte algoritmo

Convergência do Método de Jacobi O Método de Jacobi pode ser obtido de uma forma um pouco diferente da apresentada, se começarmos por decompor a matriz A :

Método de Jacobi

Condições suficientes de convergência

Condições suficientes de convergência Pensando nas duas normas matriciais que estudámos, elas serão inferiores a 1 para a matriz C se o módulo de cada elemento na diagonal de A for estritamente superior a todos os elementos na mesma linha ( no caso da norma infinito) ou na mesma coluna (no caso da norma 1). De facto, Este facto motiva a definição seguinte:

Condições suficientes de convergência: O resultado

Exemplo

Várias medidas do erro …

Método de Gauss-Seidel

Método de Gauss-Seidel

Convergência do método de Gauss-Seidel

Métodos diretos para sistemas lineares: Eliminação de Gauss O Método de eliminação de Gauss consiste na transformação do sistema linear inicial, utilizando apenas operações que não aletram as respectivas soluções, até chegar a um sistema de “fácil” resolução. Todos estes sistemas têm a mesma solução, sendo que o último é de resolução trivial.

Método de eliminação de Gauss

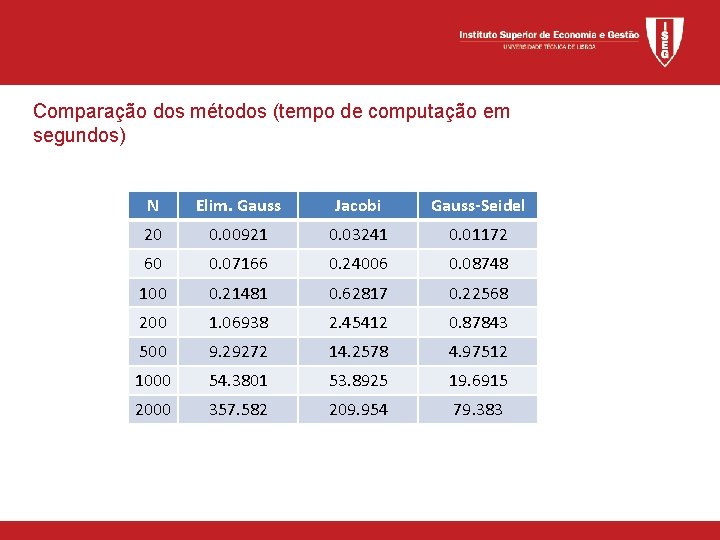
Comparação dos métodos (tempo de computação em segundos) N Elim. Gauss Jacobi Gauss-Seidel 20 0. 00921 0. 03241 0. 01172 60 0. 07166 0. 24006 0. 08748 100 0. 21481 0. 62817 0. 22568 200 1. 06938 2. 45412 0. 87843 500 9. 29272 14. 2578 4. 97512 1000 54. 3801 53. 8925 19. 6915 2000 357. 582 209. 954 79. 383

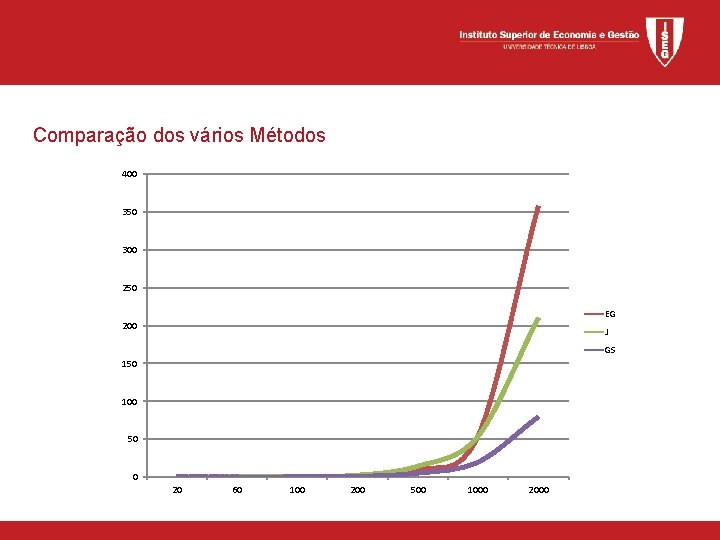
Comparação dos vários Métodos 400 350 300 250 EG 200 J GS 150 100 50 0 20 60 100 200 500 1000 2000

Condicinamento de sistemas lineares Suponhamos que pretendemos resolver o sistema linear A x = b, mas apenas dispomos de uma aproximação do segundo membro b. Isto ocorre frequentemente nas aplicações, estando normalmente ligado a erros de medição, amostragem, estamação de parâmetros, etc. O que podemos dizer sobre o erro inerente que afecta a solução deste sistema ?

Exemplo

Condicionamento Dizemos que uma matriz é bem condicionada se pequenos erros relativos nos dados conduzem a pequenos erros relativos na solução. Dizemos que uma matriz é mal condicionada se pequenos erros relativos nos dados dão origem a grandes erros relativos na solução.

Exemplo: Modelos de Leontief • Modelos lineares que descrevem uma economia com n indústrias produtivas interdependentes, cada uma delas produzindo um bem. • Para produzir esses bens, cada uma das indústrias necessita dos bens produzidos pelas outras indústrias. • Cada indústria, além de produzir o necessário para abastecer as restantes, deve ainda satisfazer uma determinada procura final do bem. • Os dados vêm normalmente agregados por ramo de actividade, com diversos níveis de agregação, a seleccionar conforme a aplicação. • Os dados podem ser expressos em unidades produzidas ou em unidades monetárias, consoante a informação disponível.

Formalização

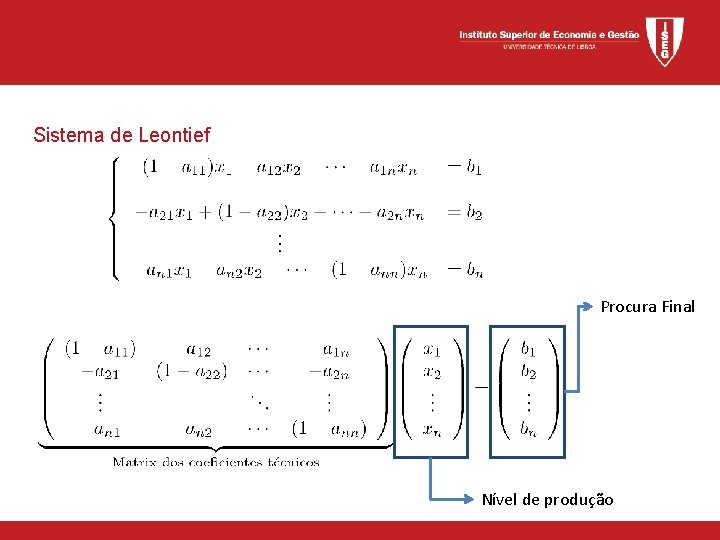
Sistema de Leontief Procura Final Nível de produção

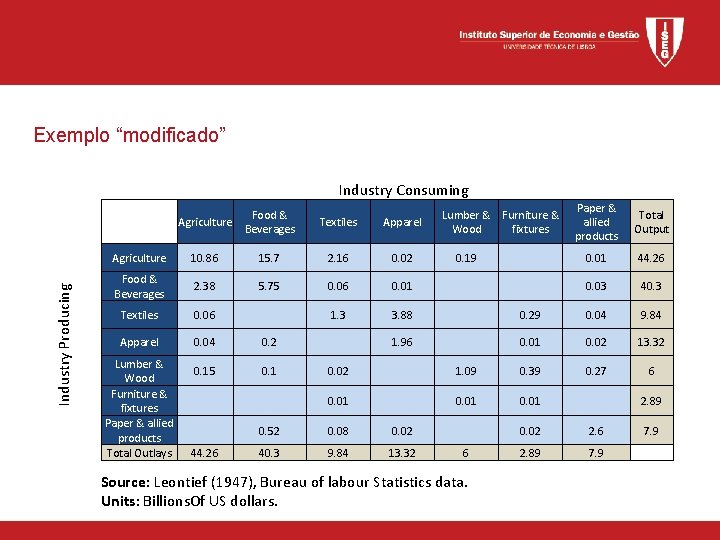
Exemplo “modificado” Industry Producing Industry Consuming Total Output Agriculture 10. 86 15. 7 2. 16 0. 02 0. 19 0. 01 44. 26 Food & Beverages 2. 38 5. 75 0. 06 0. 01 0. 03 40. 3 Textiles 0. 06 1. 3 3. 88 0. 29 0. 04 9. 84 Apparel 0. 04 0. 2 1. 96 0. 01 0. 02 13. 32 0. 15 0. 1 0. 02 1. 09 0. 39 0. 27 6 0. 01 2. 89 0. 52 0. 08 0. 02 2. 6 7. 9 44. 26 40. 3 9. 84 13. 32 6 2. 89 7. 9 Lumber & Wood Furniture & fixtures Paper & allied products Total Outlays Textiles Apparel Lumber & Furniture & Wood fixtures Paper & allied products Food & Beverages Source: Leontief (1947), Bureau of labour Statistics data. Units: Billions. Of US dollars.

Actividade 1. Construir uma matriz de coeficientes técnicos nesta situação, em que os disponíveis estão expressos em unidade monetárias, sem referência a quantidades produzidas ou ao custo unitário. 2. Identificar a procura final, por área de negócio, e resolver o sistema de Leontief correspondente. 3. Mediante os resultados obtidos, discuta a utilidade da resolução do sistema. 4. Discuta o condicionamento do sistema linear e estime o erro cometido na resolução do mesmo se as estimativas das procuras finais estiverem afectadas de um erro inferior a 10%.