Air Navigation The Triangle of Velocities Lecture Two

Air Navigation The Triangle of Velocities Lecture Two

Distance, Speed, Time We know that an aircraft travelling a distance of 600 nm at 300 kts, will take 2 hours to complete the journey. This is calculated using the Distance - Speed - Time formulae Distance DST Speed Time

Velocity and Vectors Having discussed the basics of Speed, Time and Distance in flying, it is now necessary to consider the Wind, which is simply air that is moving. But the wind can have effects on aircraft, it can blow them miles of course, and it can also cause the aircraft to speed up or slow down.

Velocity and Vectors Having discussed the basics of Speed, Time and Distance in flying, it is now necessary to consider the Wind, which is simply air that is moving. When we talk about aircraft or wind movement, we must always give both the direction and speed of the movement. Direction and speed together are called A VELOCITY

Velocity and Vectors A velocity can be represented on paper by a line called a VECTOR. The bearing of the vector line represents the direction of the movement. The length of the line represents the speed. This is expressed as Track / Speed True North Track of 015° Speed 140 kts (015/140) True North Track of 90° Speed 200 kts (090/200)

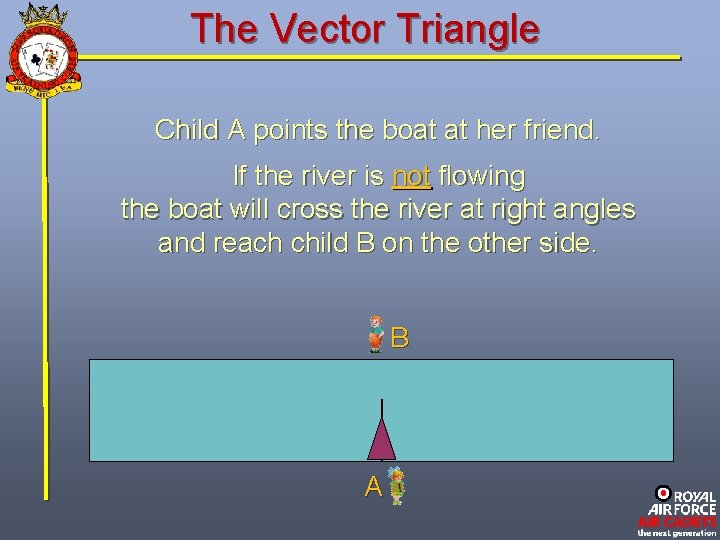
The Vector Triangle Imagine two children, on either side of a river, with a toy boat driven by an electric motor. The boat has a rudder, to keep it on a straight course, and has a speed of 2 knots. B A

The Vector Triangle Child A points the boat at her friend. If the river is not flowing the boat will cross the river at right angles and reach child B on the other side. B A

The Vector Triangle Imagine two children, on either side of a river, with a toy boat driven by an electric motor. The boat has a rudder to keep it going straight, and has a speed of 2 knots. If the river is not flowing the boat will cross the river at right angles and reach child B on the other side. B A

The Vector Triangle However, rivers flow downstream to the sea, so let’s look at a river where the speed of the current is 2 knots. Child B puts the boat back in the river, and points it at his friend. and the boat ends up at ‘C’. B A C

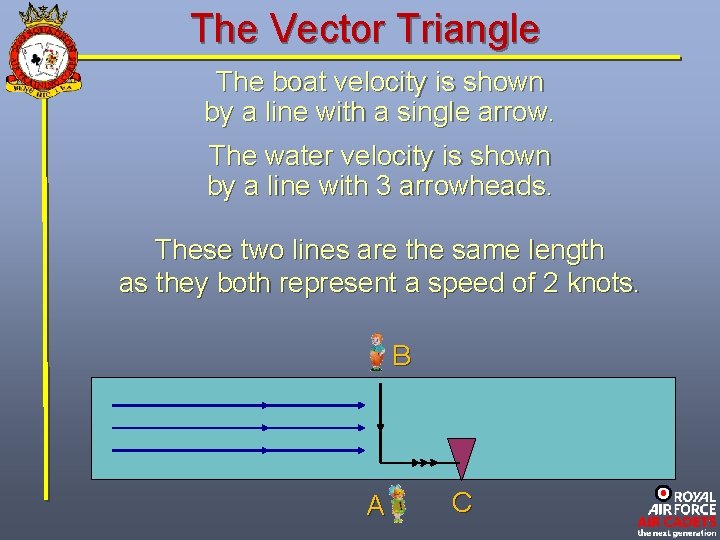
The Vector Triangle The boat velocity is shown by a line with a single arrow. The water velocity is shown by a line with 3 arrowheads. These two lines are the same length as they both represent a speed of 2 knots. B A C

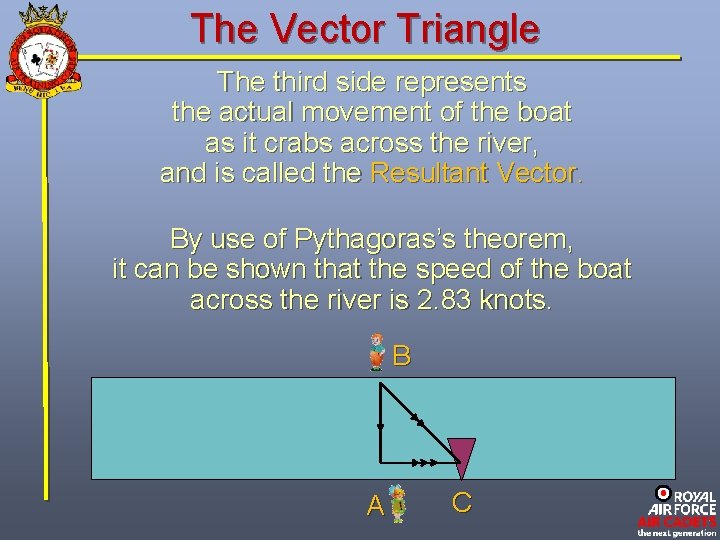
The Vector Triangle The third side represents the actual movement of the boat as it crabs across the river, and is called the Resultant Vector. By use of Pythagoras’s theorem, it can be shown that the speed of the boat across the river is 2. 83 knots. B A C

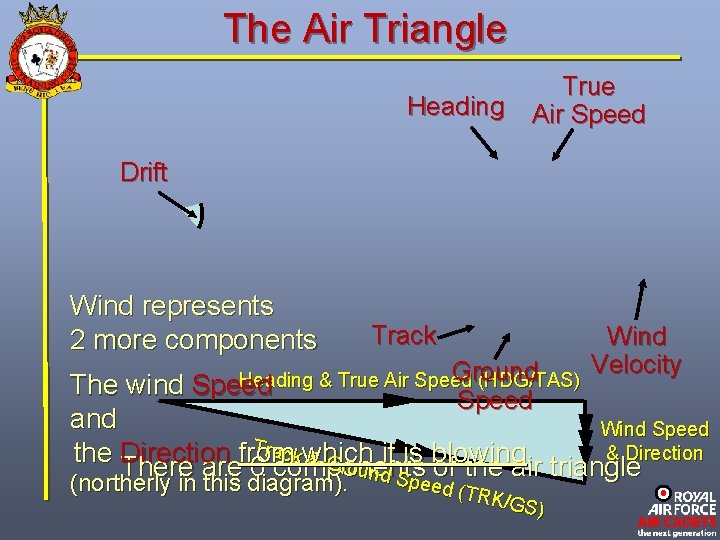
The Vector Triangle The same basic triangle can be used to show the motion of an aircraft through the air, the air itself, also moving. There are two basic differences: As aircraft speed is more than wind speed the triangle will be much longer and thinner, and the triangle is labelled with different names. Heading & True Air Speed (HDG/TAS) Track & Gro und S peed (TRK /GS) Wind Speed & Direction

The Air Triangle Heading True Air Speed Drift Wind represents 2 more components Track Wind Velocity Ground Heading & True Air Speed (HDG/TAS) The wind Speed and Wind Speed Track which it is blowing. & Direction the Direction from & Gro There are 6 components of the air triangle un (northerly in this diagram). d Spe (northerly in this diagram). ed (T RK/G S)

Wind Effects The wind can have effects on aircraft, it can blow them miles of course, and it can also cause the aircraft to speed up or slow down. To maintain a planned track and counter the effects of A Cross Wind, you must turn off into wind by an amount equal to the drift

Wind Effects The wind can have effects on aircraft, it can blow them miles of course, and it can also cause the aircraft to speed up or slow down. To maintain a planned track and counter the effects of A Head Wind, you must increase your airspeed by an amount equal to the headwind component

Wind Effects The wind can have effects on aircraft, it can blow them miles of course, and it can also cause the aircraft to speed up or slow down. To maintain a planned track and counter the effects of A Tail Wind, you must decrease your airspeed by an amount equal to the headwind component

Wind Effects The effects of Tail and Head winds can easily result in – An early ETA with a Tail Wind OR A late ETA with a Head Wind

Wind Effects SUMMARY To counter the effects of a Cross Wind, you must turn off into wind by an amount equal to the drift. To counter the effects of a Head Wind, you must increase your airspeed by an amount equal to the headwind component. To counter the effects of a Tail Wind, you must decrease your airspeed by an amount equal to the headwind component.

Real World Scenario There are three likely scenarios when we have to solve the triangle of Velocities. The first is at the planning stage of a flight, to calculate how long the flight will take. The second scenario is in the air, to calculate the Wind Velocity. The final scenario occurs when you are over a featureless area such as the sea, when you can calculate a Deduced Reckoning (DR) position.

Real World Scenario In the planning stage of a flight, given 4 of the 6 elements of the Triangle of Velocities True Air Speed, Track, Wind Speed and Direction it is now possible to solve the other two, Ground Speed and Heading and then use the DST formula to calculate how long the flight will take.

Real World Scenario When the aircraft is in the air, we know the True Air Speed and Heading, and we can measure out our Track and Ground Speed by watching our position over the ground. From these 4 elements, we can calculate the Wind Velocity. (Speed and Direction)

Real World Scenario When you know the Heading and True Air Speed, and have a reliable Wind Velocity. From these 4 elements you can calculate your Track and Ground Speed to produce a Deduced Reckoning position (DR) by applying the time from your last known position to the Ground Speed to give a distance along your Track.

Check Understanding On paper, what is a vector representative of? Direction and Speed Direction and Time and Speed Only Direction

Check Understanding What is meant by the term Velocity? Time and Distance Direction and Speed and Time Distance and Direction

Check Understanding A vector is a line drawn to represent a velocity. This is achieved by. . . The bearing of the line representing the direction and the length representing the speed The length represents mph at all times The bearing of the line representing the speed and the length representing direction The bearing represents knots at all times

Check Understanding In the air triangle of velocities, What is the angle between the heading and the track vector known as? Drift Velocity Ground Speed Wind Direction

Check Understanding In the air triangle below, name the components of the 3 rd side, shown by a dotted line. Heading and TAS Track and Ground Speed Wind Speed and Direction Velocity

Check Understanding In the air triangle of velocities, the heading vector has 2 components. What are they? Heading and Drift Heading and Ground Speed Heading and True Air Speed Heading and Direction

Check Understanding In the air triangle below, name the components of the 3 rd side, shown by a dotted line. Heading and TAS Track and Ground Speed Wind Speed and Direction Drift and Ground Speed

Check Understanding In the air triangle of velocities, there are 6 components. How many are needed to calculate the missing ones? 2 3 4 5

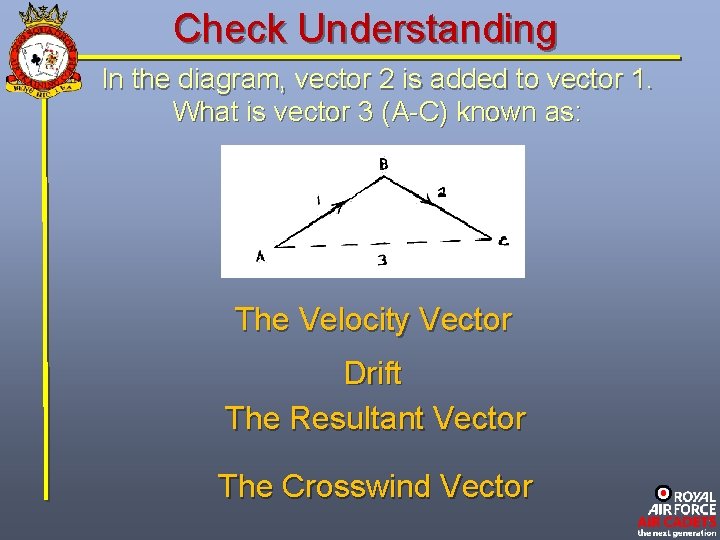
Check Understanding In the diagram, vector 2 is added to vector 1. What is vector 3 (A-C) known as: The Velocity Vector Drift The Resultant Vector The Crosswind Vector

Check Understanding To maintain a planned track how would you counter the effects of a cross wind? Use the planned track as the heading Turn off into wind by an amount equal to the drift Take no action and accept the error Turn off down wind by an amount equal to the drift

Check Understanding What effect would a head wind have on an ETA calculated for still air conditions? You will be early on ETA Push you off track You will be late on ETA It will have no effect

Check Understanding To maintain time in a headwind what must you do to your airspeed and by how much? Increase it by an amount equal to the headwind component Increase it by an amount equal to the drift Decrease it by an amount equal to the headwind component Do nothing

Air Navigation End of Presentation