TRIANGLE Segitiga Triangle Around Us Definition of triangle

TRIANGLE Segitiga

Triangle Around Us

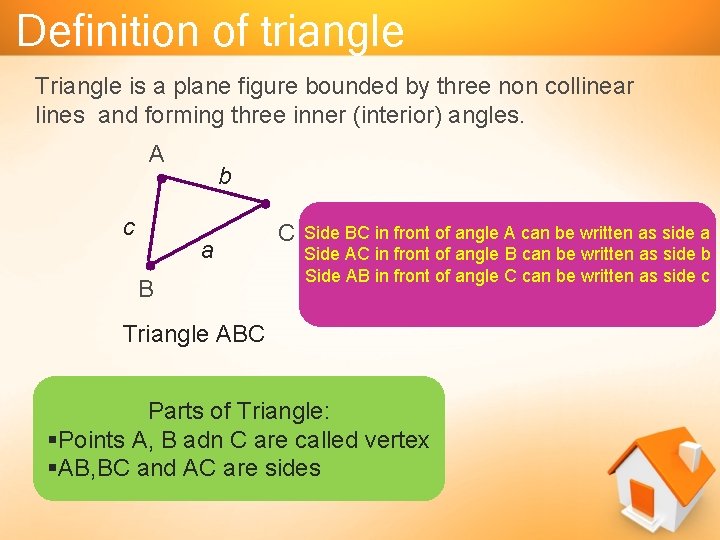
Definition of triangle Triangle is a plane figure bounded by three non collinear lines and forming three inner (interior) angles. A c b a B C Side BC in front of angle A can be written as side a Side AC in front of angle B can be written as side b Side AB in front of angle C can be written as side c Triangle ABC Parts of Triangle: §Points A, B adn C are called vertex §AB, BC and AC are sides

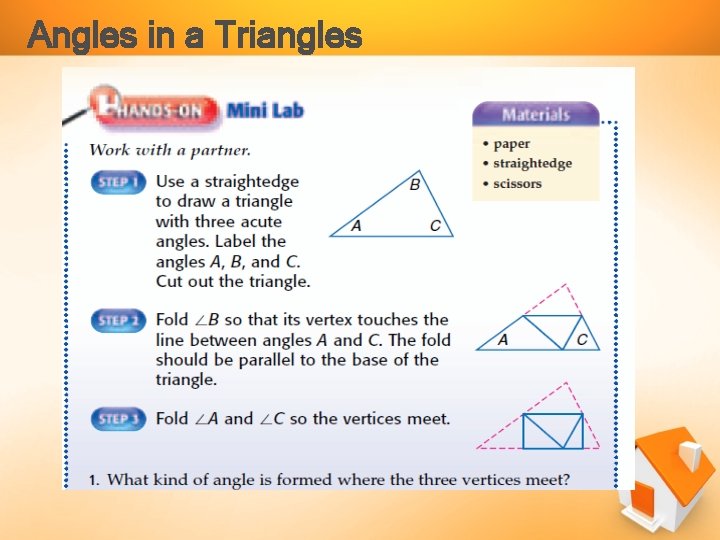
Angles in a Triangles

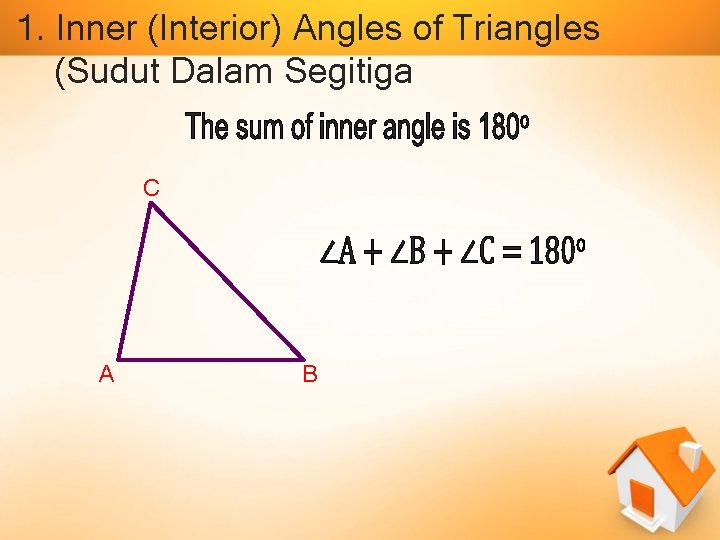
1. Inner (Interior) Angles of Triangles (Sudut Dalam Segitiga C A B

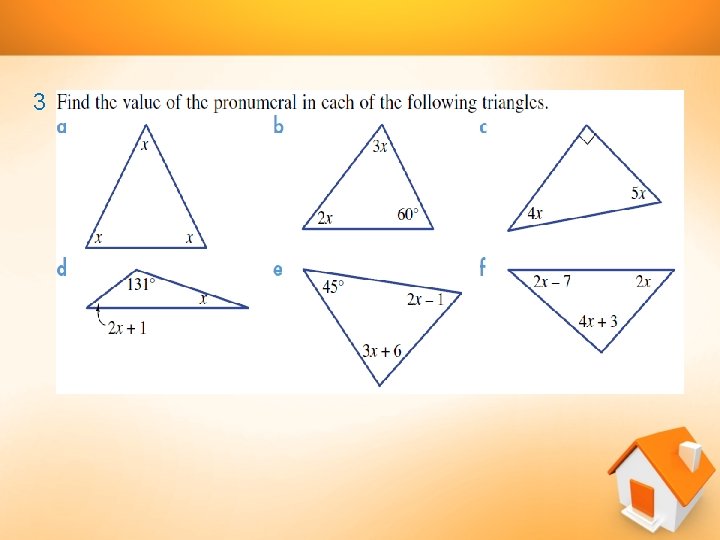
EXERCISES-1

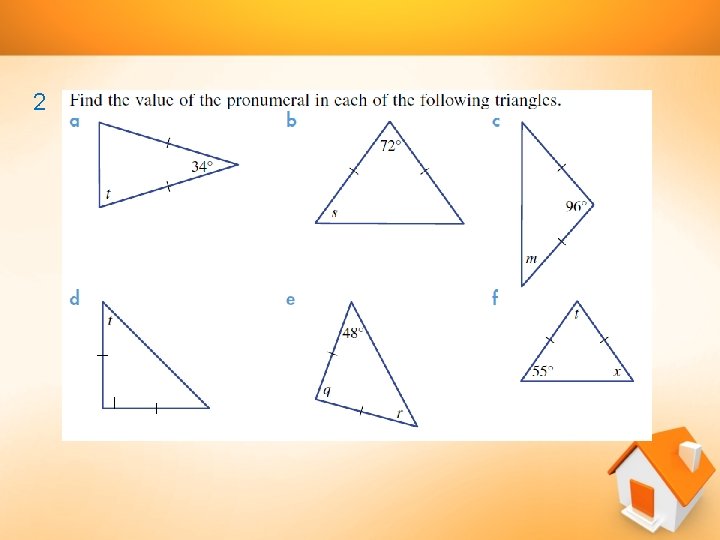
2

3

4 5 6

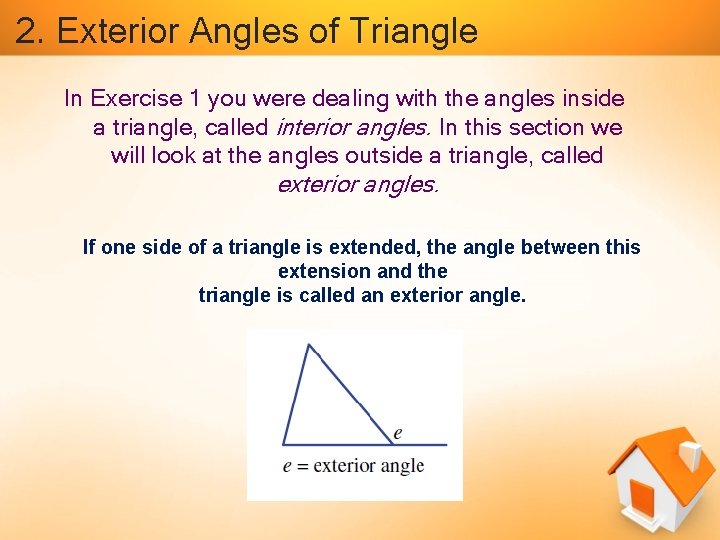
2. Exterior Angles of Triangle In Exercise 1 you were dealing with the angles inside a triangle, called interior angles. In this section we will look at the angles outside a triangle, called exterior angles. If one side of a triangle is extended, the angle between this extension and the triangle is called an exterior angle.

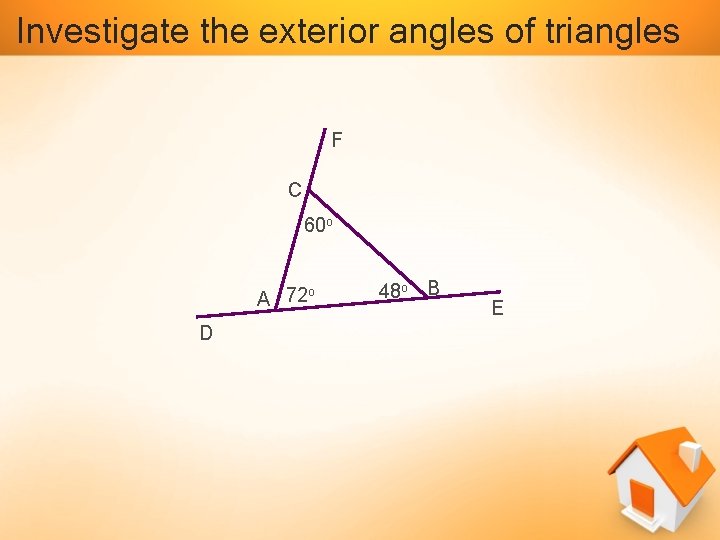
Investigate the exterior angles of triangles F C 60 o A 72 o D 48 o B E

Conclusion

1 2 3

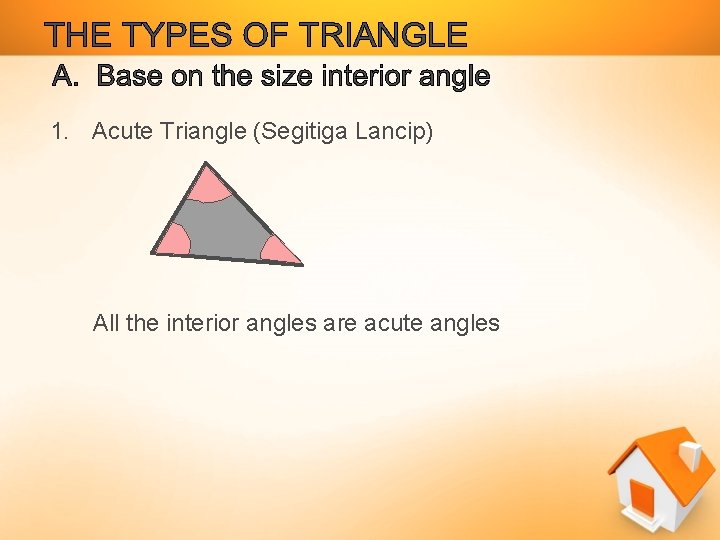
1. Acute Triangle (Segitiga Lancip) All the interior angles are acute angles

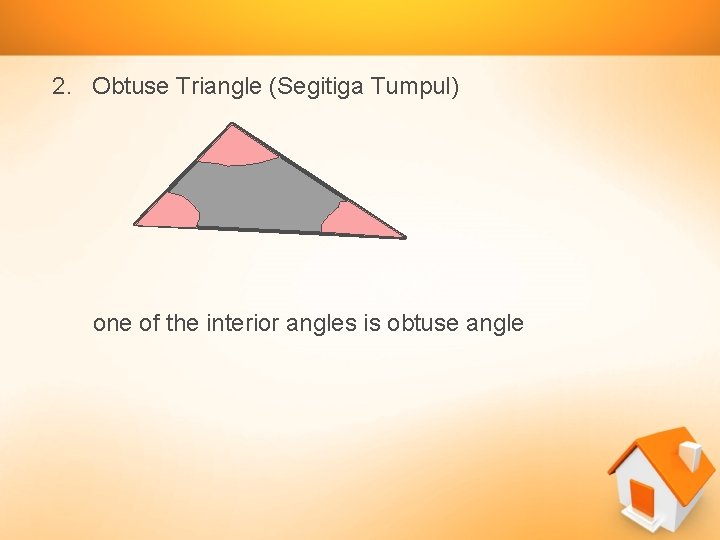
2. Obtuse Triangle (Segitiga Tumpul) one of the interior angles is obtuse angle

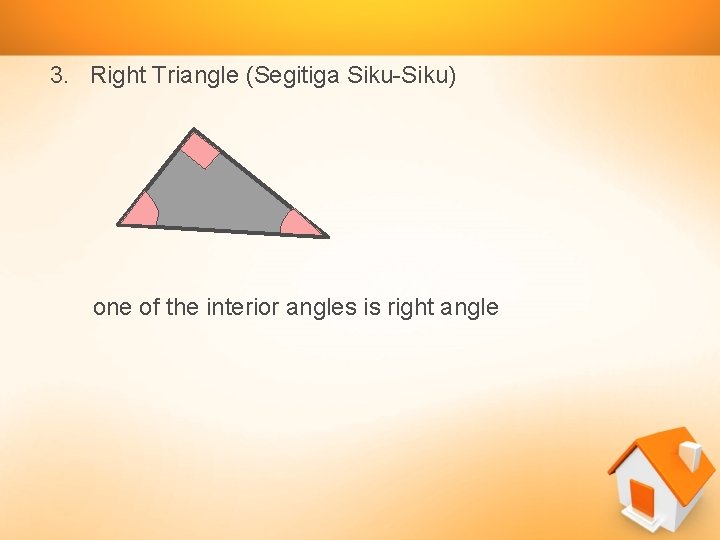
3. Right Triangle (Segitiga Siku-Siku) one of the interior angles is right angle

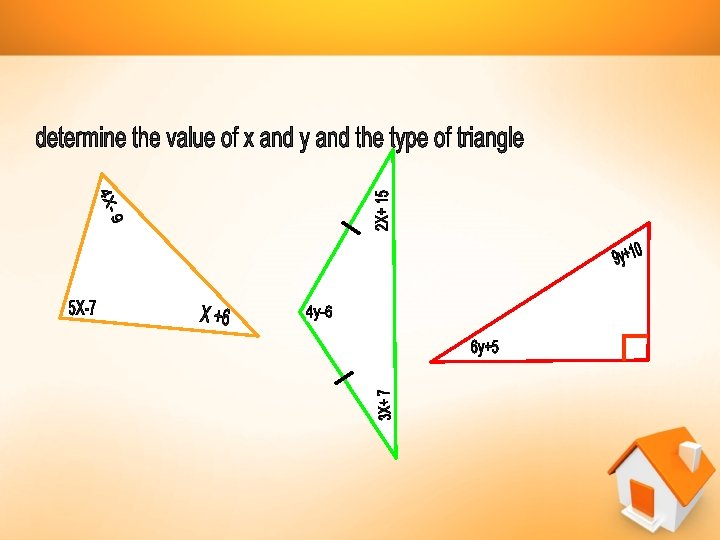
Exercise • Determine the type of triangle bellow if 1. The angle are : 65, 35, 80 2. The angle are : 25, 60, 95 3. The angle are : 54, 56, 70 4. Two angle are : 73, 34, 5. The ratio of angle is 3 : 4 : 5 6. The ratio of angle is 2 : 3 : 4 7. The angle is 6 x, 2 x + 3, 4 x +9

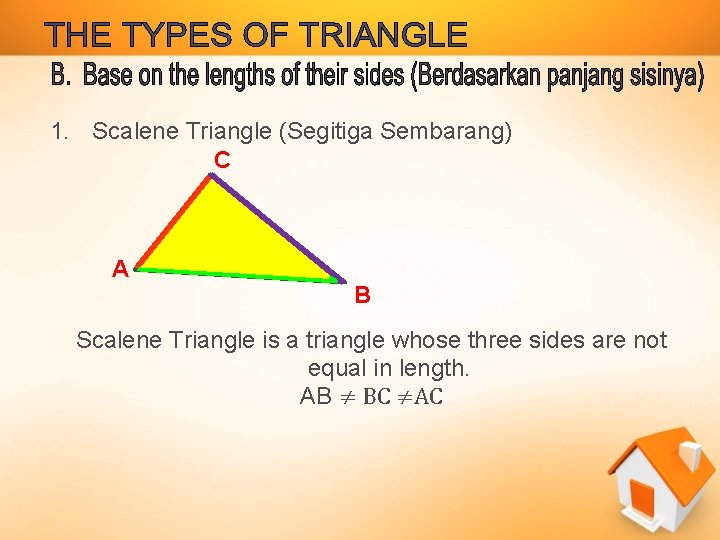
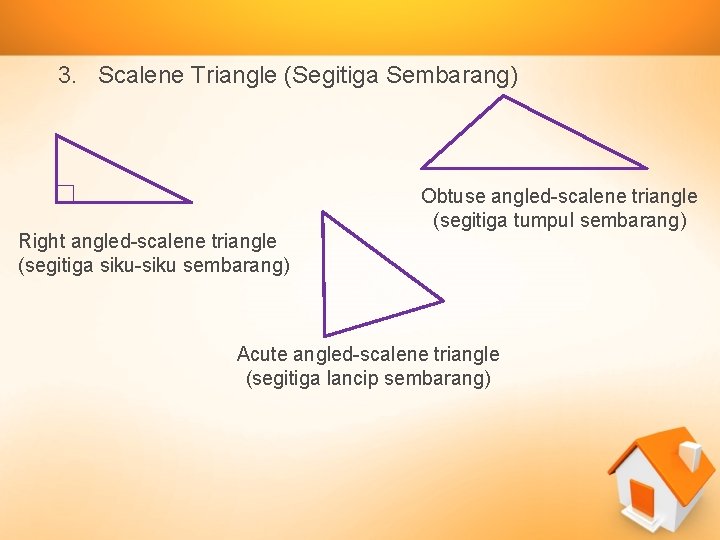
1. Scalene Triangle (Segitiga Sembarang) C A B Scalene Triangle is a triangle whose three sides are not equal in length. AB ≠ BC ≠AC

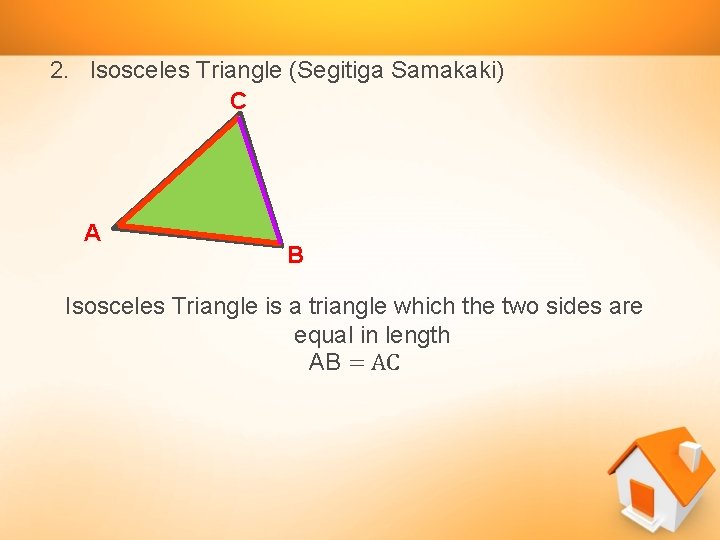
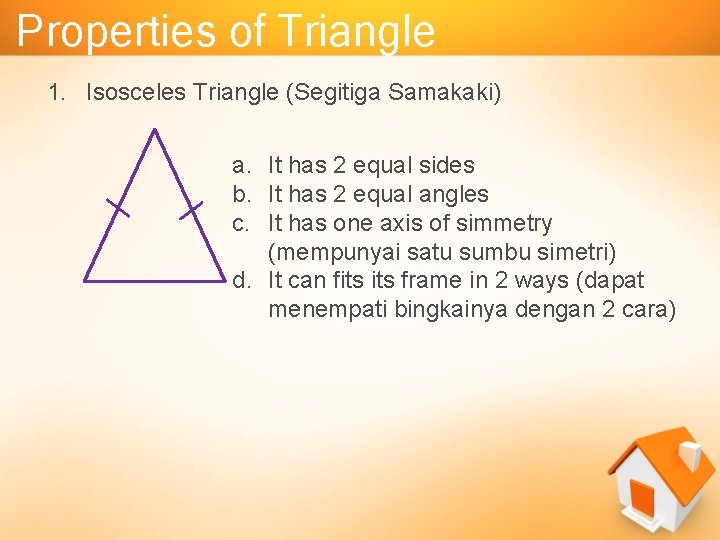
2. Isosceles Triangle (Segitiga Samakaki) C A B Isosceles Triangle is a triangle which the two sides are equal in length AB = AC

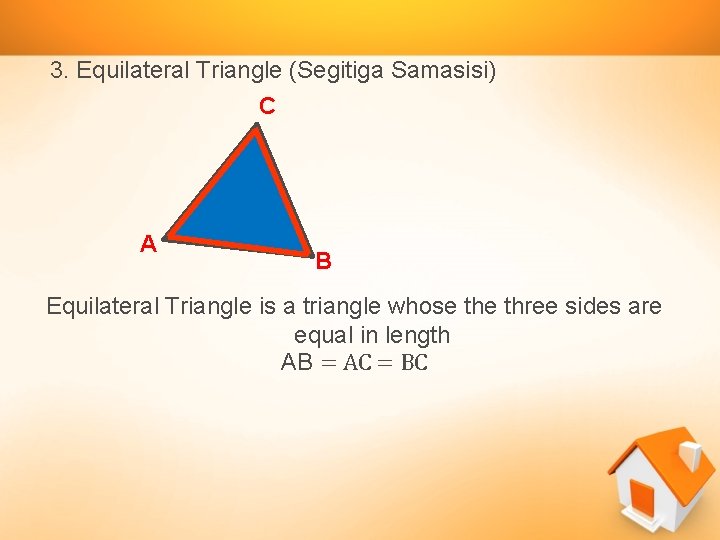
3. Equilateral Triangle (Segitiga Samasisi) C A B Equilateral Triangle is a triangle whose three sides are equal in length AB = AC = BC

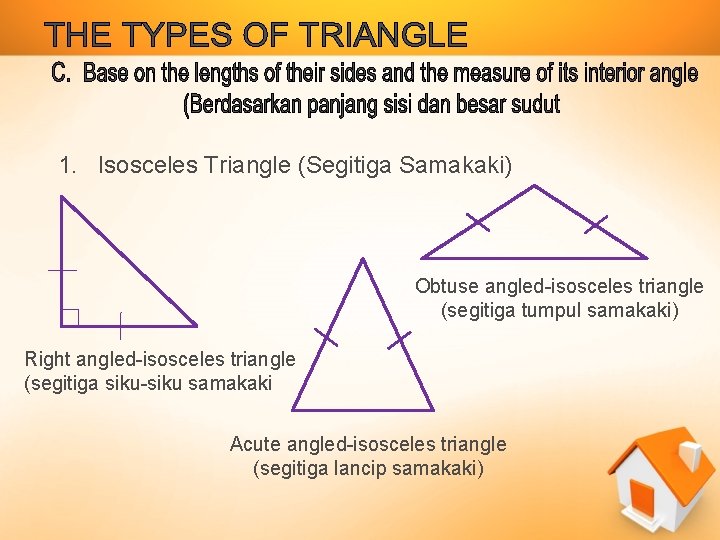
1. Isosceles Triangle (Segitiga Samakaki) Obtuse angled-isosceles triangle (segitiga tumpul samakaki) Right angled-isosceles triangle (segitiga siku-siku samakaki Acute angled-isosceles triangle (segitiga lancip samakaki)

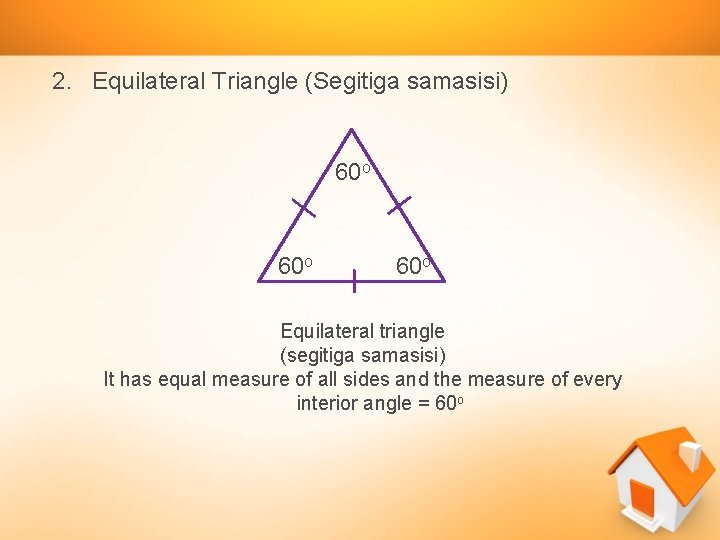
2. Equilateral Triangle (Segitiga samasisi) 60 o 60 o Equilateral triangle (segitiga samasisi) It has equal measure of all sides and the measure of every interior angle = 60 o

3. Scalene Triangle (Segitiga Sembarang) Right angled-scalene triangle (segitiga siku-siku sembarang) Obtuse angled-scalene triangle (segitiga tumpul sembarang) Acute angled-scalene triangle (segitiga lancip sembarang)

Answer the following questions 1. Is there a right-angled equilateral triangle? (adakah segitiga siku-siku samasisi? ) 2. Is there a obtuse-angled equilateral triangle? (adakah segitiga tumpul samasisi? ) 3. Is there a acute-angled scalene triangle? (adakah segitiga lancip sembarang? ) 4. Is an equilateral triangle always an acute triangle?

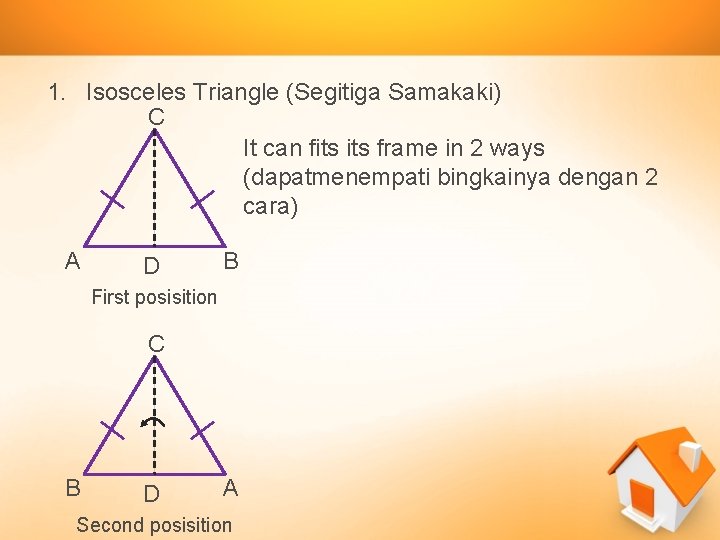
Properties of Triangle 1. Isosceles Triangle (Segitiga Samakaki) a. It has 2 equal sides b. It has 2 equal angles c. It has one axis of simmetry (mempunyai satu sumbu simetri) d. It can fits frame in 2 ways (dapat menempati bingkainya dengan 2 cara)

1. Isosceles Triangle (Segitiga Samakaki) C It can fits frame in 2 ways (dapatmenempati bingkainya dengan 2 cara) A D B First posisition C B D A Second posisition

Properties of Triangle 2. Equilateral Triangle (Segitiga Samasisi) Answer the following questions: a. How many equal sides are in equilateral triangle? b. How many equal angles are in equilateral triangle? c. How many axis of simmetry are in equilateral triangle? d. In how many ways it can fits frame?

2. Equilateral Triangle (Segitiga Samasisi) a. It has 3 equal sides b. It has 3 equal angles c. It has 3 axis of simmetry (mempunyai 3 sumbu simetri) d. It can fits frame in 6 ways (dapat menempati bingkainya dengan 6 cara)

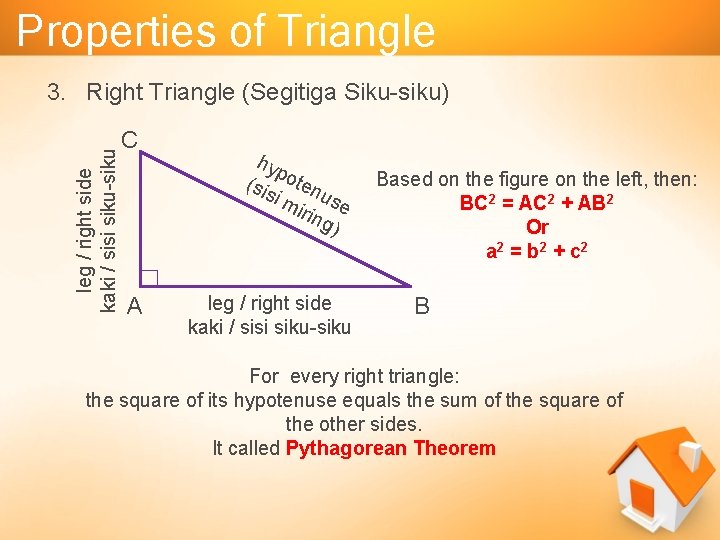
Properties of Triangle leg / right side kaki / sisi siku-siku 3. Right Triangle (Segitiga Siku-siku) C A hyp (sis oten i m use irin g) leg / right side kaki / sisi siku-siku Based on the figure on the left, then: BC 2 = AC 2 + AB 2 Or a 2 = b 2 + c 2 B For every right triangle: the square of its hypotenuse equals the sum of the square of the other sides. It called Pythagorean Theorem

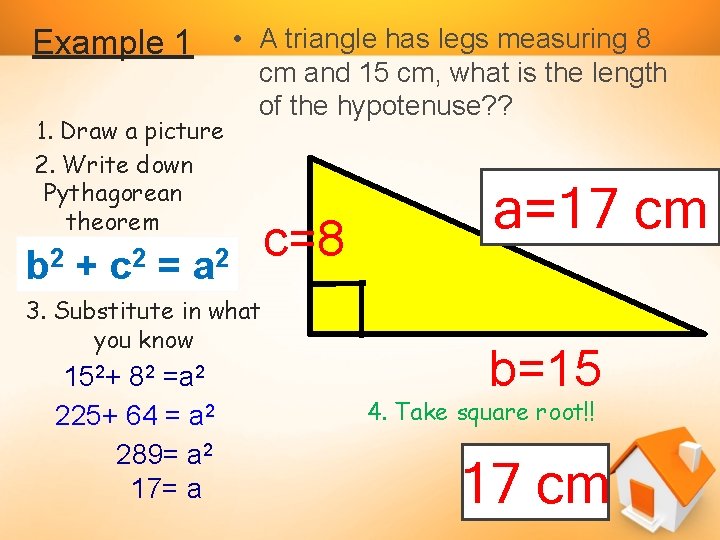
Example 1 1. Draw a picture 2. Write down Pythagorean theorem b 2 + c 2 = • A triangle has legs measuring 8 cm and 15 cm, what is the length of the hypotenuse? ? a 2 3. Substitute in what you know 152+ 82 =a 2 225+ 64 = a 2 289= a 2 17= a c=8 ? cm a=17 b=15 4. Take square root!! 17 cm

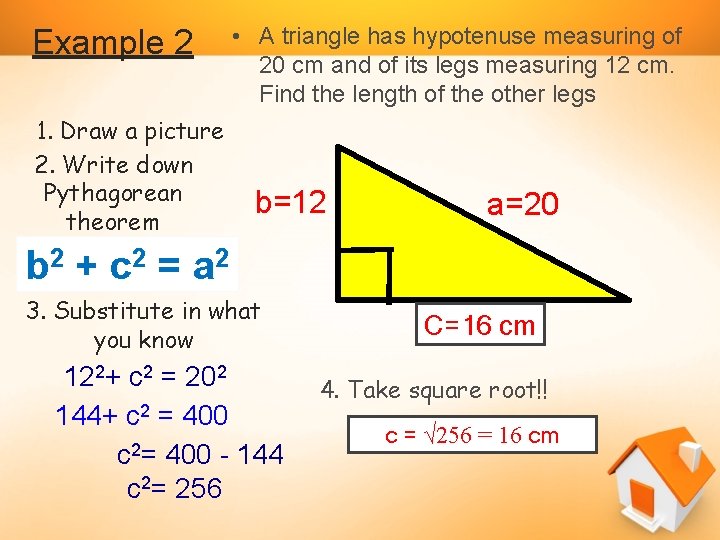
Example 2 1. Draw a picture 2. Write down Pythagorean theorem • A triangle has hypotenuse measuring of 20 cm and of its legs measuring 12 cm. Find the length of the other legs b=12 a=20 b 2 + c 2 = a 2 3. Substitute in what you know 122+ c 2 = 202 144+ c 2 = 400 c 2= 400 - 144 c 2= 256 C=16 ? cm 4. Take square root!! c = √ 256 = 16 cm

Problem 1 Based on the following figure, form the equation using Pythagorean Theorem

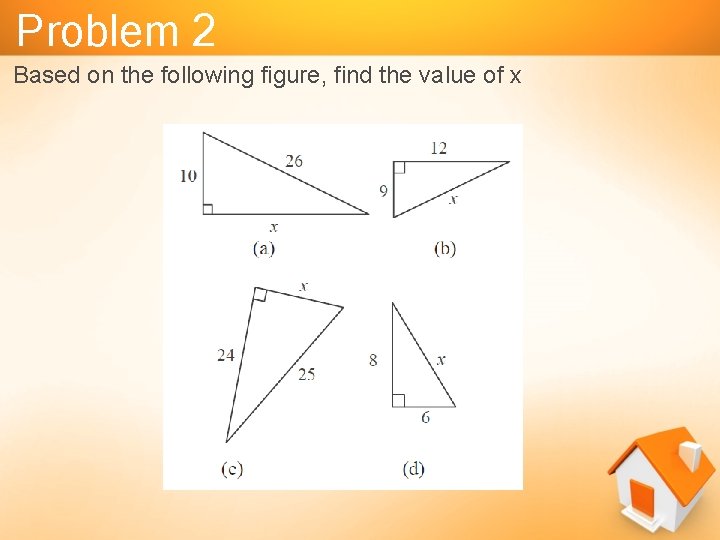
Problem 2 Based on the following figure, find the value of x

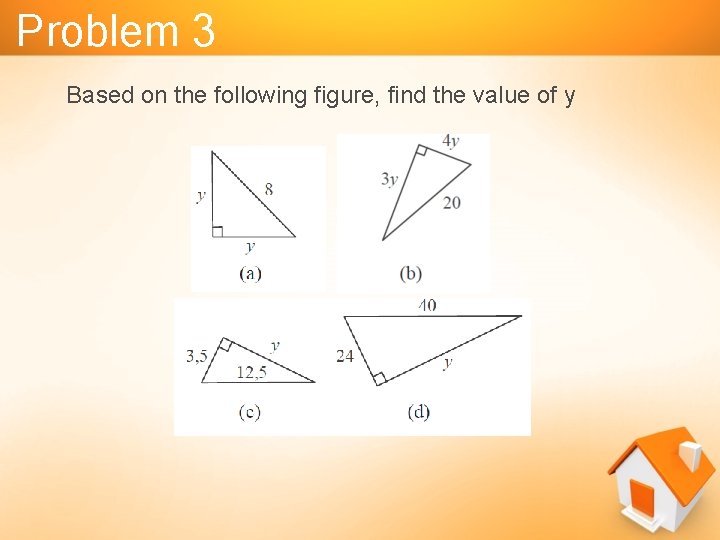
Problem 3 Based on the following figure, find the value of y

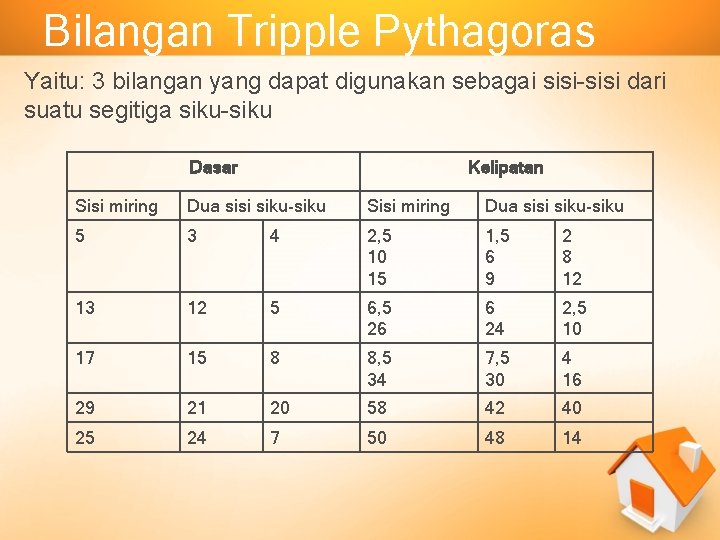
Bilangan Tripple Pythagoras Yaitu: 3 bilangan yang dapat digunakan sebagai sisi-sisi dari suatu segitiga siku-siku Dasar Kelipatan Sisi miring Dua sisi siku-siku 5 3 4 2, 5 10 15 1, 5 6 9 2 8 12 13 12 5 6, 5 26 6 24 2, 5 10 17 15 8 8, 5 34 7, 5 30 4 16 29 21 20 58 42 40 25 24 7 50 48 14

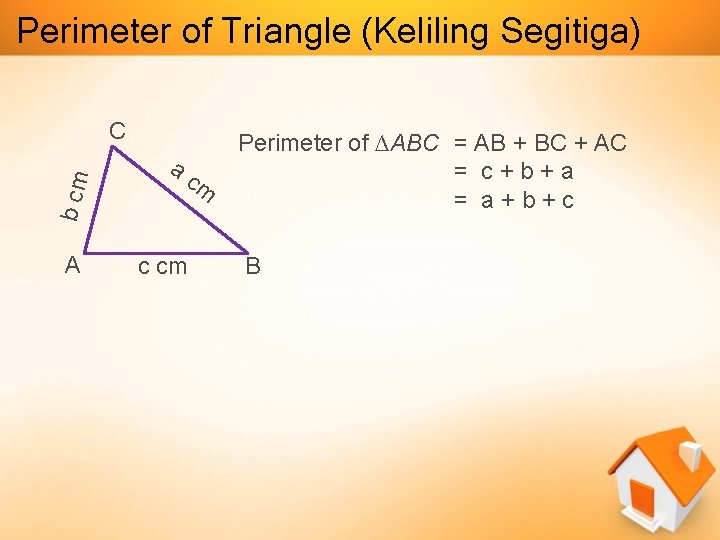
Perimeter of Triangle (Keliling Segitiga) b cm C A a cm c cm Perimeter of ∆ABC = AB + BC + AC = c+b+a = a+b+c B

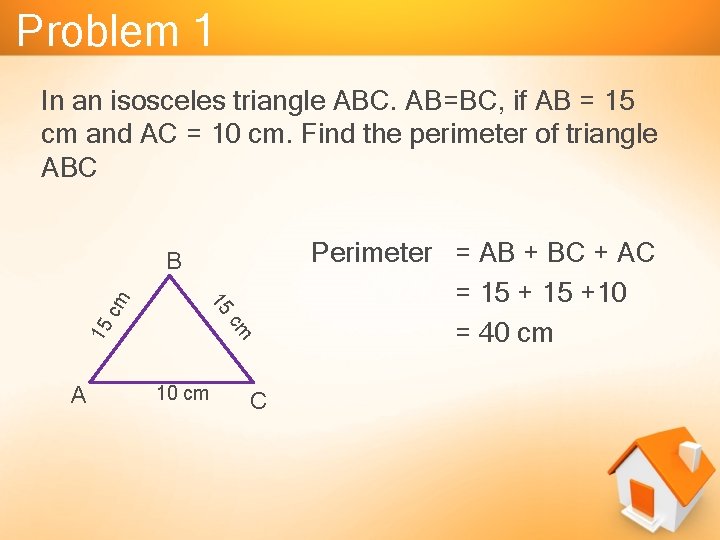
Problem 1 In an isosceles triangle ABC. AB=BC, if AB = 15 cm and AC = 10 cm. Find the perimeter of triangle ABC 15 cm B A 10 cm C Perimeter = AB + BC + AC = 15 +10 = 40 cm

Problem 2 The perimeter of triangle ABC is 120 cm. If AB: BC: AC=3: 4: 5, the length of AB is…. Solution: AB + BC + AC = 120 cm AB = (3/12) x 120 cm = 30 cm.

Problem 3 The perimeter of triangle ABC is 84 cm. If a : b : c = 5 : 3 : 4, the length of BC is….

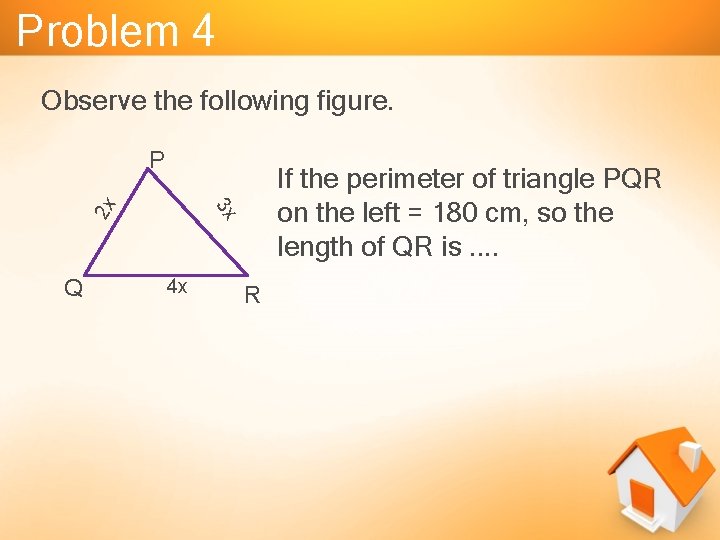
Problem 4 Observe the following figure. Q If the perimeter of triangle PQR on the left = 180 cm, so the length of QR is. . 3 x 2 x P 4 x R

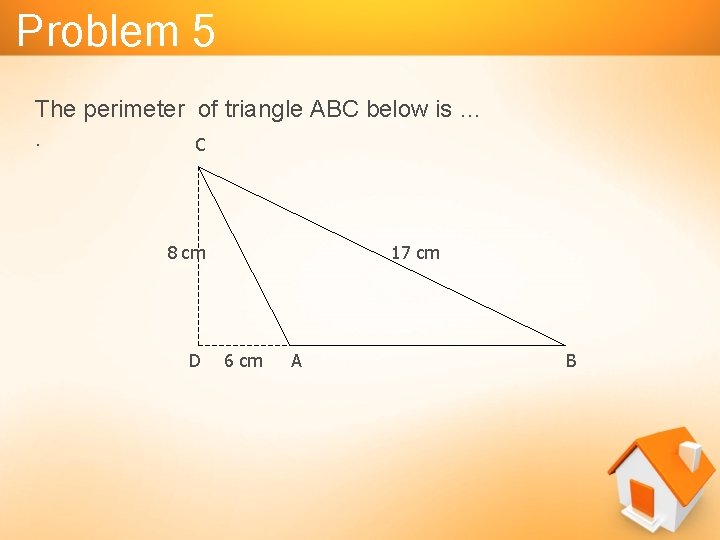
Problem 5 The perimeter of triangle ABC below is …. C 8 cm D 17 cm 6 cm A B

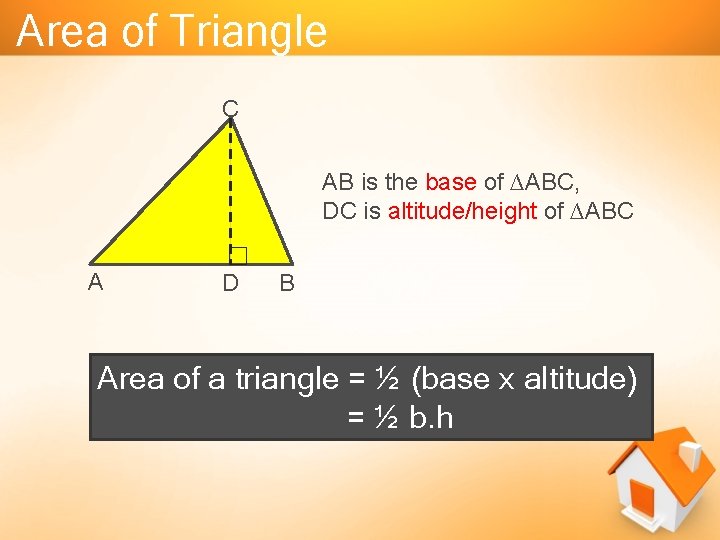
Area of Triangle C AB is the base of ∆ABC, DC is altitude/height of ∆ABC A D B Area of a triangle = ½ (base x altitude) = ½ b. h

Example: R S If PQ = 10 cm, RS= 12 cm and PR = 13 cm. The area of ∆PQR is…. P Q Solution The area of ∆PQR = ½ x base. height = ½ x PQ. RS = ½ x 10 x 12 = 60 cm 2

Problem 1 The ratio of base and altitude of a triangle is 4 : 5. If the area of the triangle is 90 cm 2, then find the base and altitude of the triangle. Solution: Area 90 90 9 3 = ½. b. h = ½. 4 x. 5 x = 10 x 2 =x 5 x 4 x

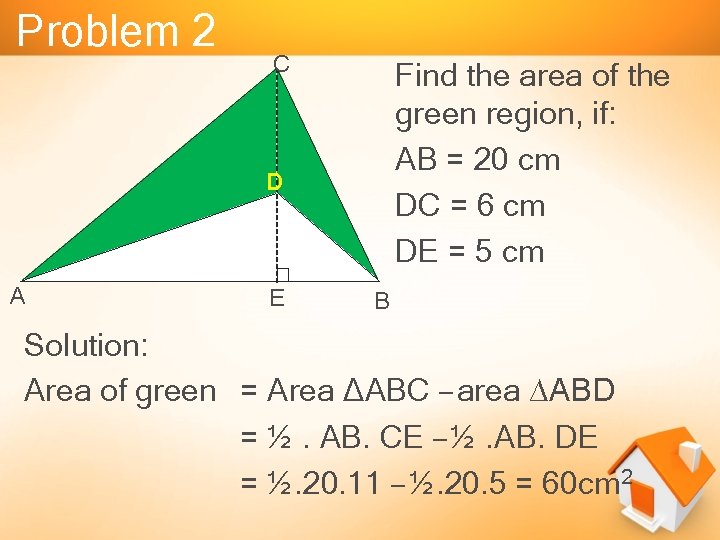
Problem 2 C Find the area of the green region, if: AB = 20 cm DC = 6 cm DE = 5 cm D A E B Solution: Area of green = Area ∆ABC – area ∆ABD = ½. AB. CE – ½. AB. DE = ½. 20. 11 – ½. 20. 5 = 60 cm 2

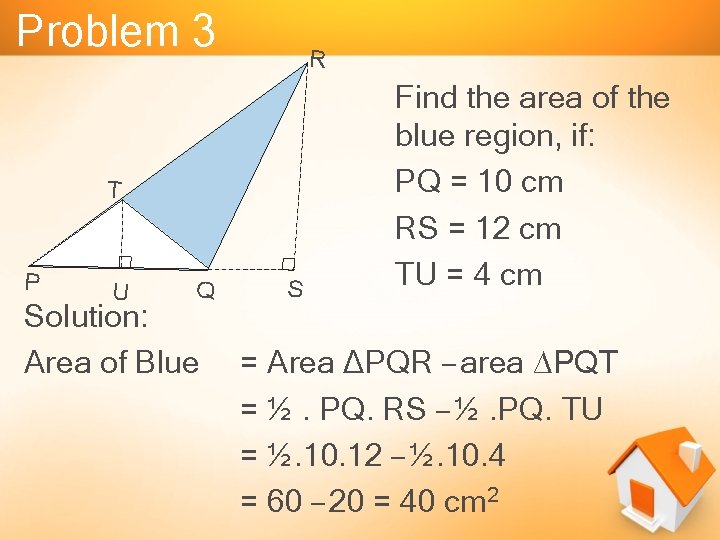
Problem 3 R T P U Q Solution: Area of Blue S Find the area of the blue region, if: PQ = 10 cm RS = 12 cm TU = 4 cm = Area ∆PQR – area ∆PQT = ½. PQ. RS – ½. PQ. TU = ½. 10. 12 – ½. 10. 4 = 60 – 20 = 40 cm 2

Problem 4 The ratio of right sides of a right triangle is 3 : 4. if the area of the triangle is 150 cm 2, find the perimeter of the triangle. Solution: Area = ½. b. h 150 = ½. 3 x. 4 x 150 = 6 x 2 25 = x 2 5 =x 4 x 3 x The right sides are : 15 cm and 20 cm. Using pythagorean theorem, the length of hypotenuse = 25 cm Perimeter = 15 cm + 20 cm + 25 cm = 60 cm

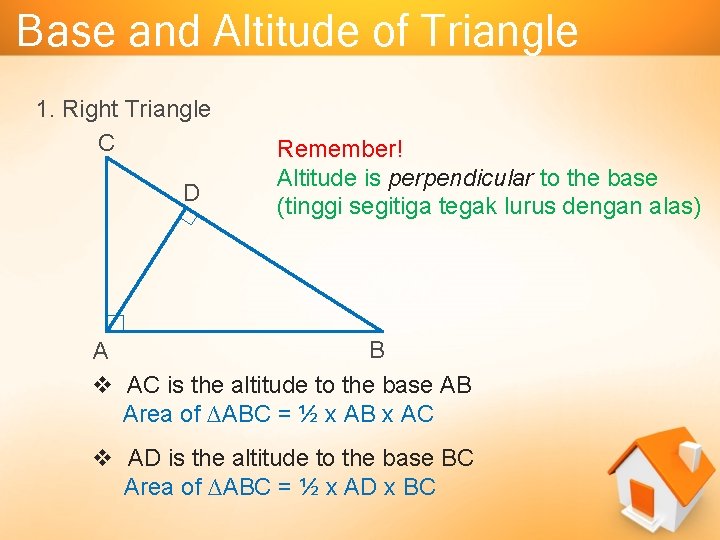
Base and Altitude of Triangle 1. Right Triangle C D Remember! Altitude is perpendicular to the base (tinggi segitiga tegak lurus dengan alas) B A v AC is the altitude to the base AB Area of ∆ABC = ½ x AB x AC v AD is the altitude to the base BC Area of ∆ABC = ½ x AD x BC

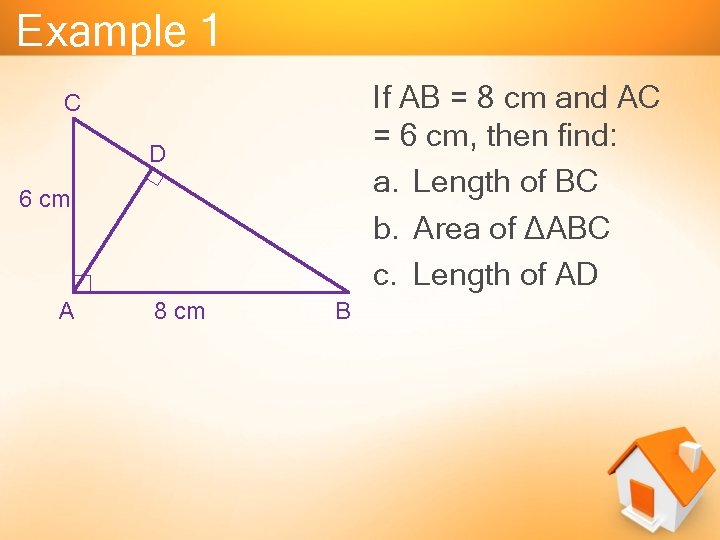
Example 1 If AB = 8 cm and AC = 6 cm, then find: a. Length of BC b. Area of ∆ABC c. Length of AD C D 6 cm A 8 cm B

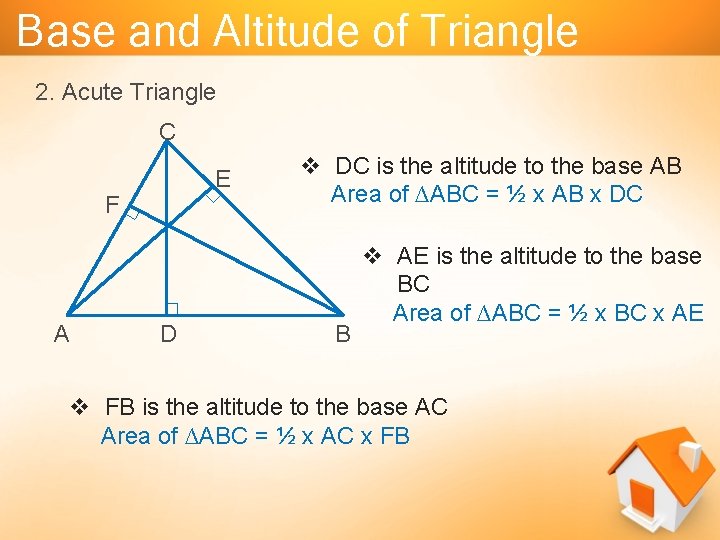
Base and Altitude of Triangle 2. Acute Triangle C E F A D v DC is the altitude to the base AB Area of ∆ABC = ½ x AB x DC B v AE is the altitude to the base BC Area of ∆ABC = ½ x BC x AE v FB is the altitude to the base AC Area of ∆ABC = ½ x AC x FB

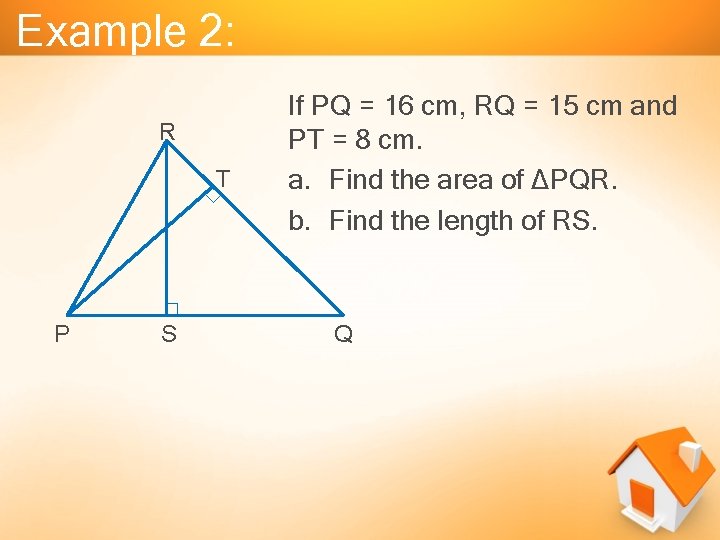
Example 2: R T P S If PQ = 16 cm, RQ = 15 cm and PT = 8 cm. a. Find the area of ∆PQR. b. Find the length of RS. Q

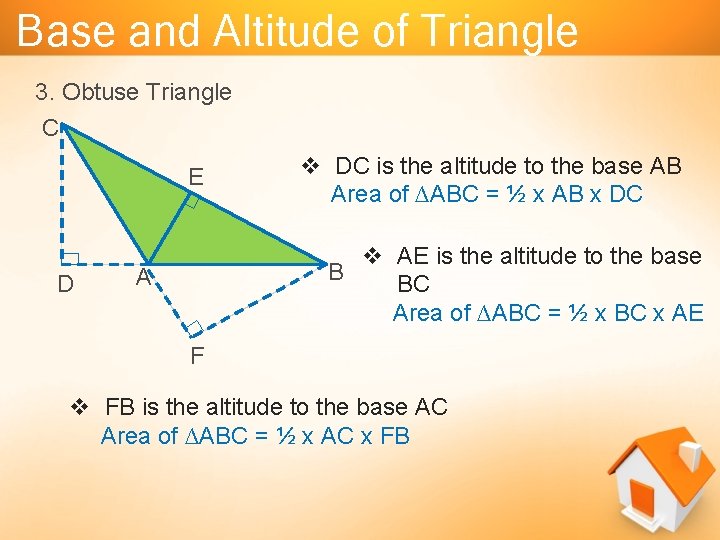
Base and Altitude of Triangle 3. Obtuse Triangle C E D v DC is the altitude to the base AB Area of ∆ABC = ½ x AB x DC v AE is the altitude to the base B BC Area of ∆ABC = ½ x BC x AE A F v FB is the altitude to the base AC Area of ∆ABC = ½ x AC x FB

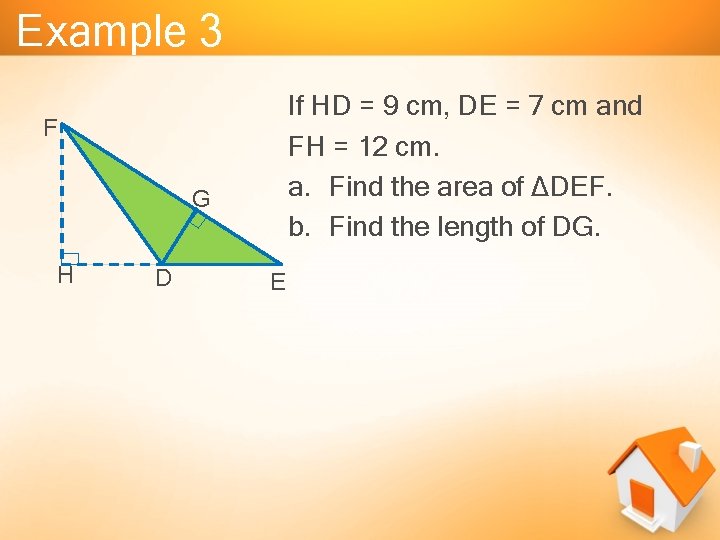
Example 3 If HD = 9 cm, DE = 7 cm and FH = 12 cm. a. Find the area of ∆DEF. b. Find the length of DG. F G H D E

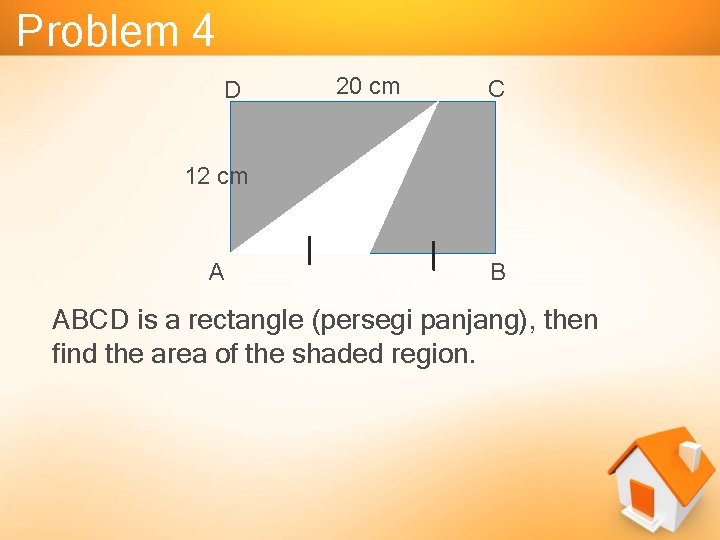
Problem 4 D 20 cm C 12 cm A B ABCD is a rectangle (persegi panjang), then find the area of the shaded region.