UNIDADE 8 Isometrias do plano 8 4 Rotao


![Na figura acima, estão representados o triângulo [ABC] e o ponto O. Na figura acima, estão representados o triângulo [ABC] e o ponto O.](https://slidetodoc.com/presentation_image_h2/828c6214e3928027cef0e524fa5ca5ae/image-18.jpg)
![Vamos construir o transformado do triângulo [ABC] através de uma rotação de centro O Vamos construir o transformado do triângulo [ABC] através de uma rotação de centro O](https://slidetodoc.com/presentation_image_h2/828c6214e3928027cef0e524fa5ca5ae/image-19.jpg)
![Abre o compasso com a medida do comprimento do segmento [OA]. Abre o compasso com a medida do comprimento do segmento [OA].](https://slidetodoc.com/presentation_image_h2/828c6214e3928027cef0e524fa5ca5ae/image-22.jpg)
![O triângulo [A’B’C’] resulta da rotação de centro em O e ângulo 90º no O triângulo [A’B’C’] resulta da rotação de centro em O e ângulo 90º no](https://slidetodoc.com/presentation_image_h2/828c6214e3928027cef0e524fa5ca5ae/image-34.jpg)

![Repara que: Pelo critério LLL, os triângulos [ABC] e [A’B’C’] são iguais, logo, as Repara que: Pelo critério LLL, os triângulos [ABC] e [A’B’C’] são iguais, logo, as](https://slidetodoc.com/presentation_image_h2/828c6214e3928027cef0e524fa5ca5ae/image-37.jpg)

- Slides: 38

UNIDADE 8 Isometrias do plano

8. 4 Rotação

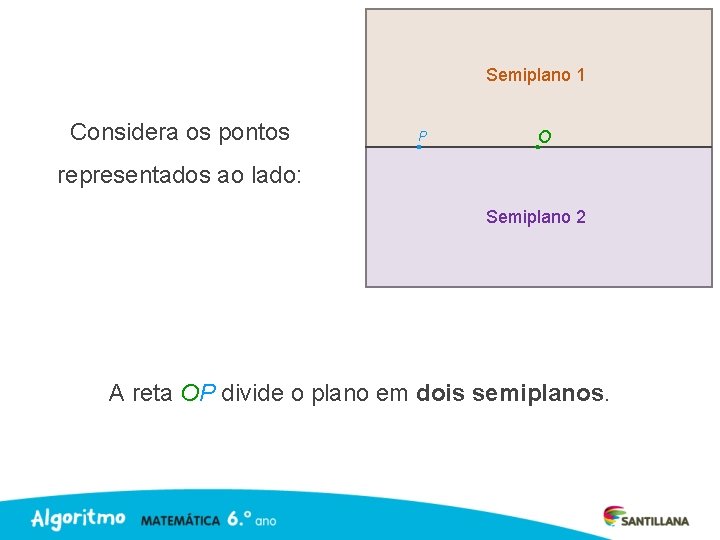
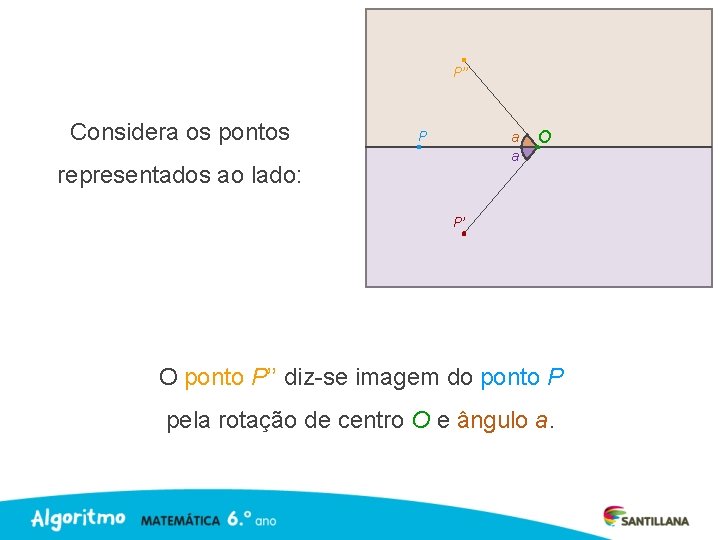
Semiplano 1 Considera os pontos P O representados ao lado: Semiplano 2 A reta OP divide o plano em dois semiplanos.

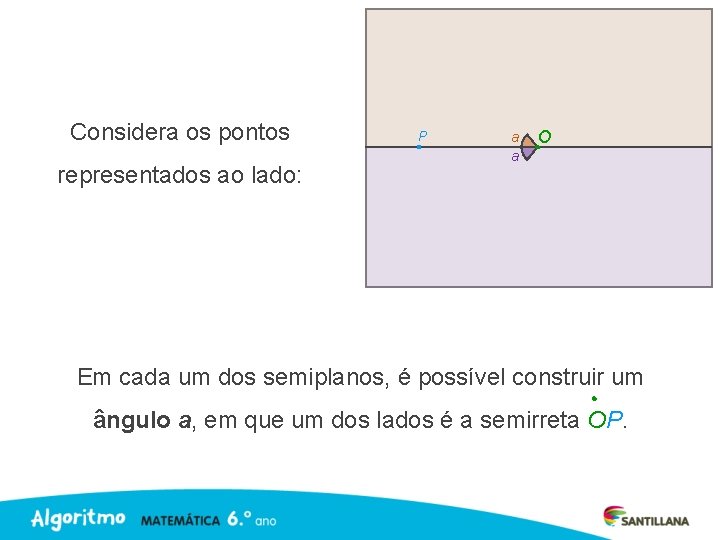
Considera os pontos representados ao lado: P a a O Em cada um dos semiplanos, é possível construir um ângulo a, em que um dos lados é a semirreta OP.

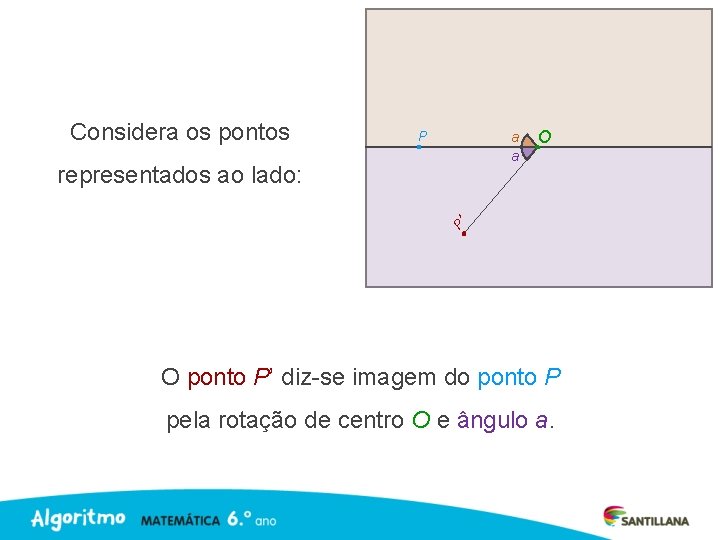
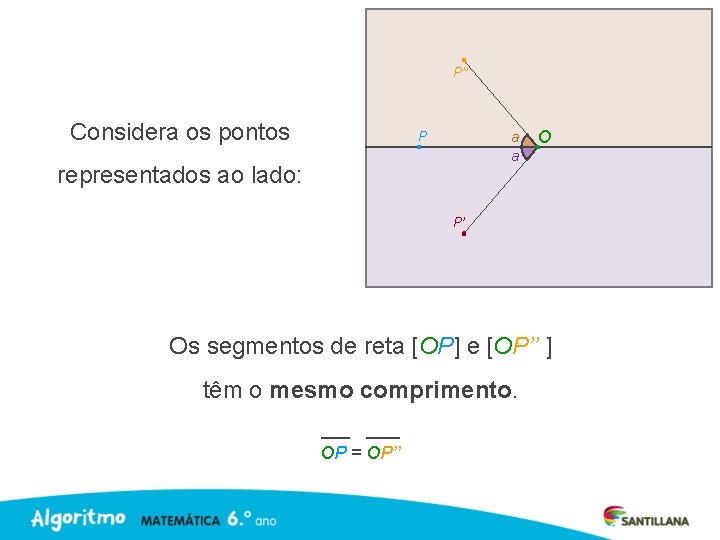
Considera os pontos P a a P’ representados ao lado: O O ponto P’ diz-se imagem do ponto P pela rotação de centro O e ângulo a.

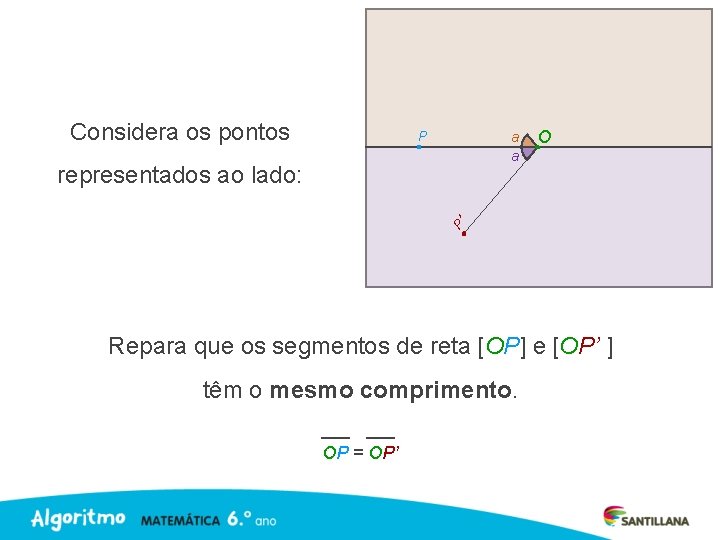
Considera os pontos P a a P’ representados ao lado: O Repara que os segmentos de reta [OP] e [OP’ ] têm o mesmo comprimento. OP = OP’

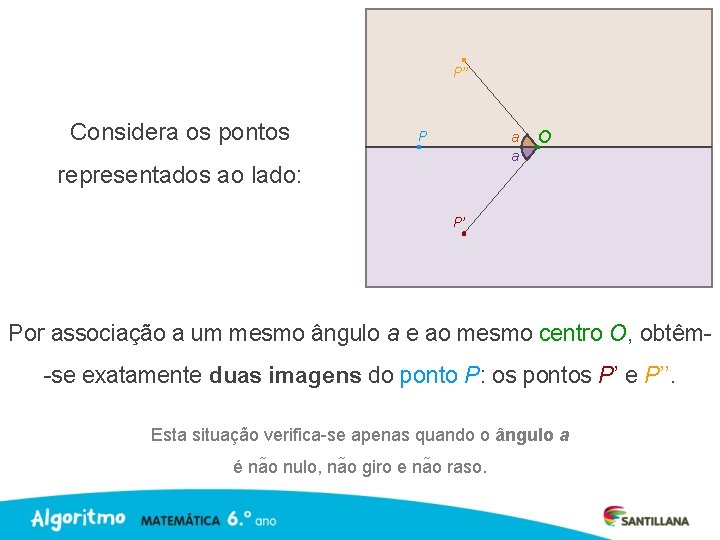
P’’ Considera os pontos P a a representados ao lado: O P’ O ponto P’’ diz-se imagem do ponto P pela rotação de centro O e ângulo a.

P’’ Considera os pontos P a a representados ao lado: O P’ Os segmentos de reta [OP] e [OP’’ ] têm o mesmo comprimento. OP = OP’’

P’’ Considera os pontos P a a representados ao lado: O P’ Por associação a um mesmo ângulo a e ao mesmo centro O, obtêm-se exatamente duas imagens do ponto P: os pontos P’ e P’’. Esta situação verifica-se apenas quando o ângulo a é na o nulo, na o giro e na o raso.

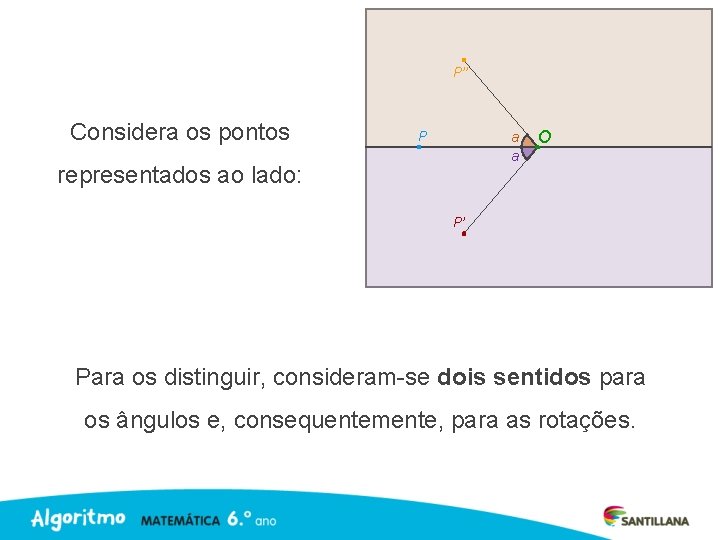
P’’ Considera os pontos P a a representados ao lado: O P’ Para os distinguir, consideram-se dois sentidos para os ângulos e, consequentemente, para as rotações.

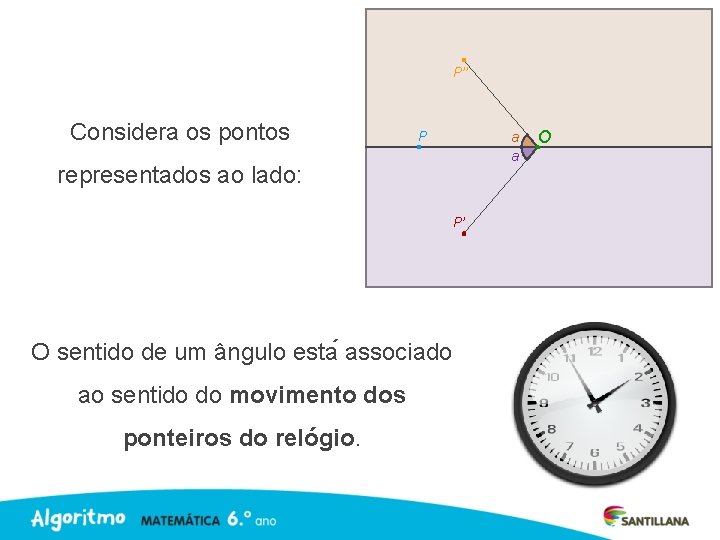
P’’ Considera os pontos P a a representados ao lado: P’ O sentido de um ângulo esta associado ao sentido do movimento dos ponteiros do relógio. O

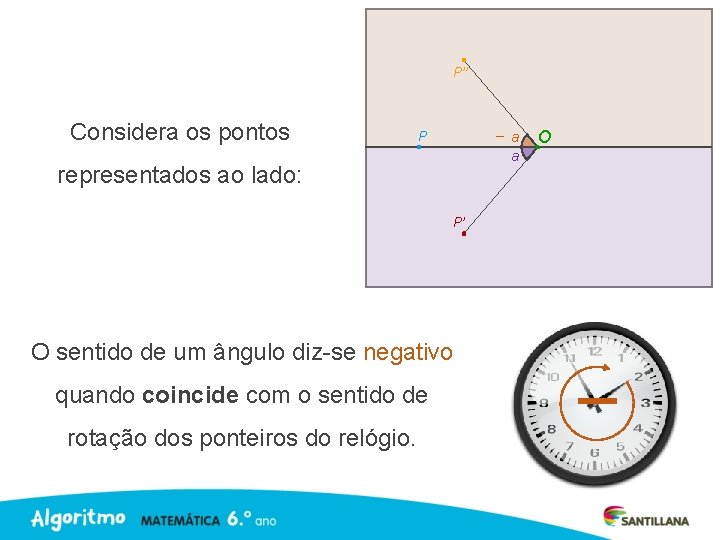
P’’ Considera os pontos – a a P representados ao lado: O P’ O sentido de um ângulo diz-se negativo quando coincide com o sentido de rotação dos ponteiros do relógio. –

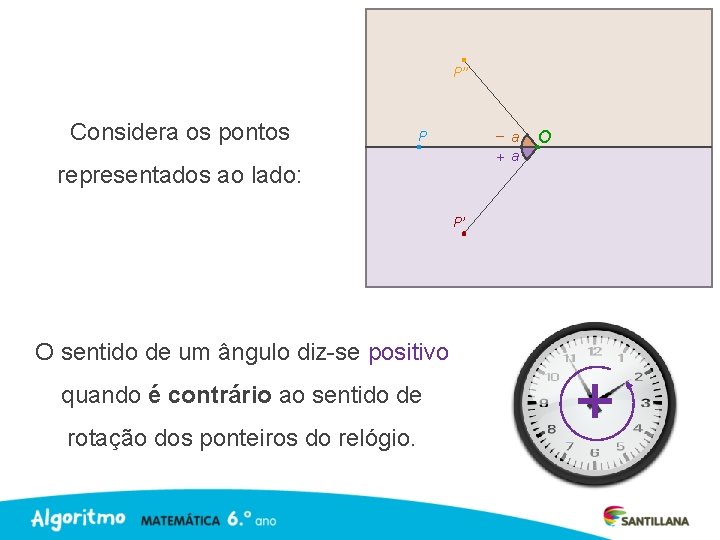
P’’ Considera os pontos – a + a P representados ao lado: O P’ O sentido de um ângulo diz-se positivo quando é contrário ao sentido de rotação dos ponteiros do relógio. +

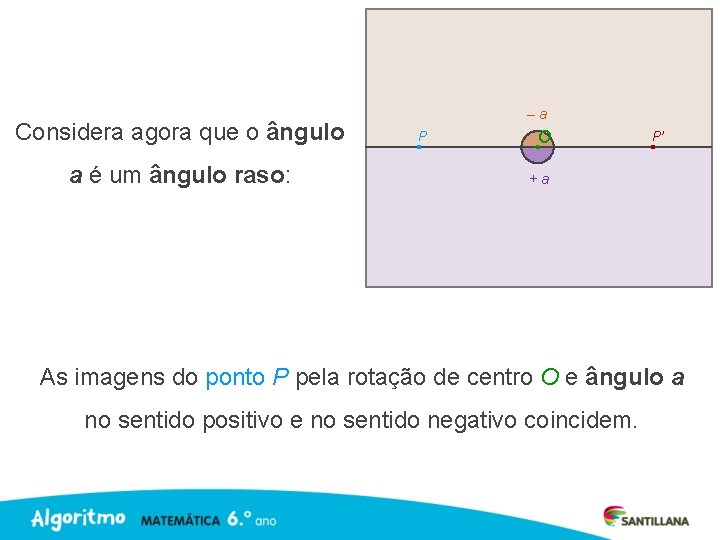
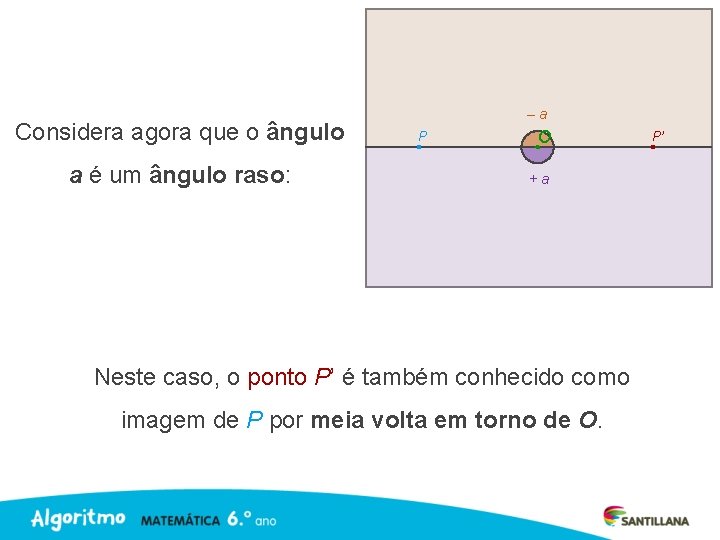
Considera agora que o ângulo a é um ângulo raso: –a P O P’ +a As imagens do ponto P pela rotação de centro O e ângulo a no sentido positivo e no sentido negativo coincidem.

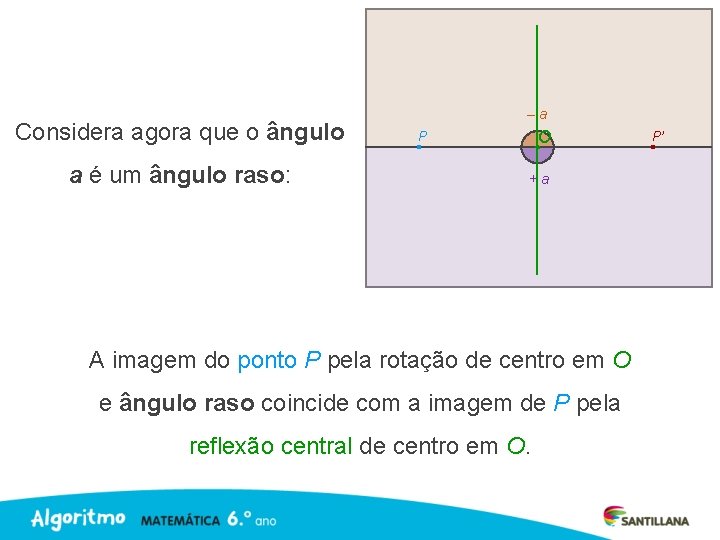
Considera agora que o ângulo a é um ângulo raso: –a P O +a Neste caso, o ponto P’ é também conhecido como imagem de P por meia volta em torno de O. P’

Considera agora que o ângulo a é um ângulo raso: –a O P +a A imagem do ponto P pela rotação de centro em O e ângulo raso coincide com a imagem de P pela reflexão central de centro em O. P’

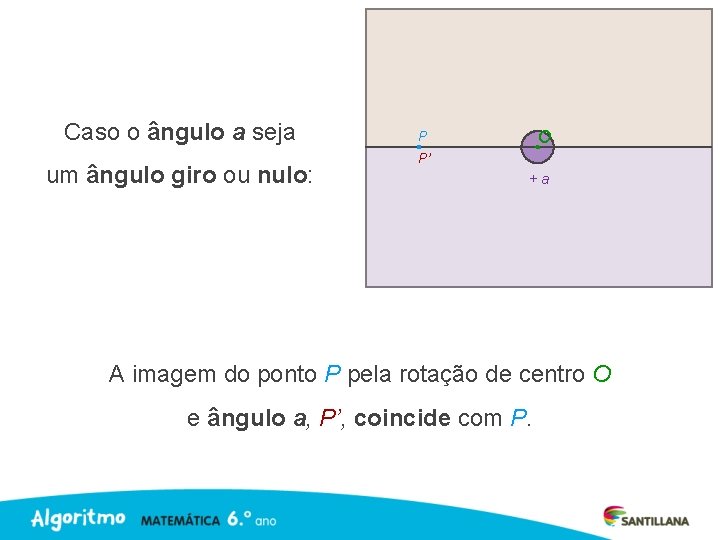
Caso o ângulo a seja um ângulo giro ou nulo: O P P’ +a A imagem do ponto P pela rotação de centro O e ângulo a, P’, coincide com P.
![Na figura acima estão representados o triângulo ABC e o ponto O Na figura acima, estão representados o triângulo [ABC] e o ponto O.](https://slidetodoc.com/presentation_image_h2/828c6214e3928027cef0e524fa5ca5ae/image-18.jpg)
Na figura acima, estão representados o triângulo [ABC] e o ponto O.
![Vamos construir o transformado do triângulo ABC através de uma rotação de centro O Vamos construir o transformado do triângulo [ABC] através de uma rotação de centro O](https://slidetodoc.com/presentation_image_h2/828c6214e3928027cef0e524fa5ca5ae/image-19.jpg)
Vamos construir o transformado do triângulo [ABC] através de uma rotação de centro O e amplitude 90º no sentido positivo.

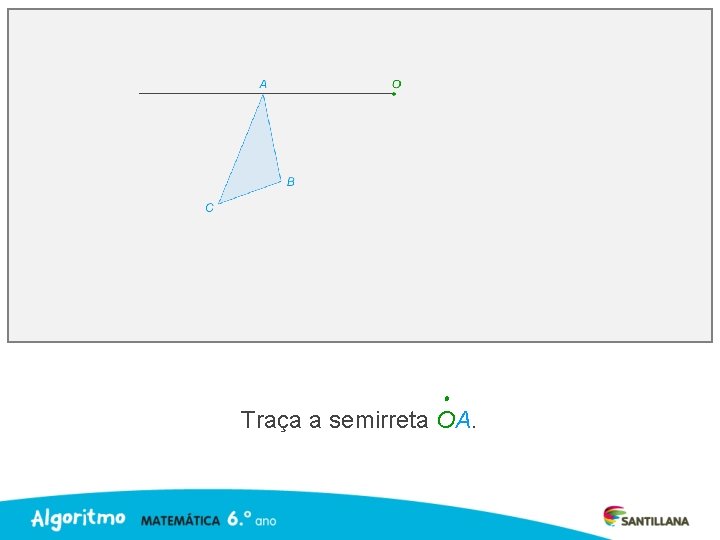
Traça a semirreta OA.

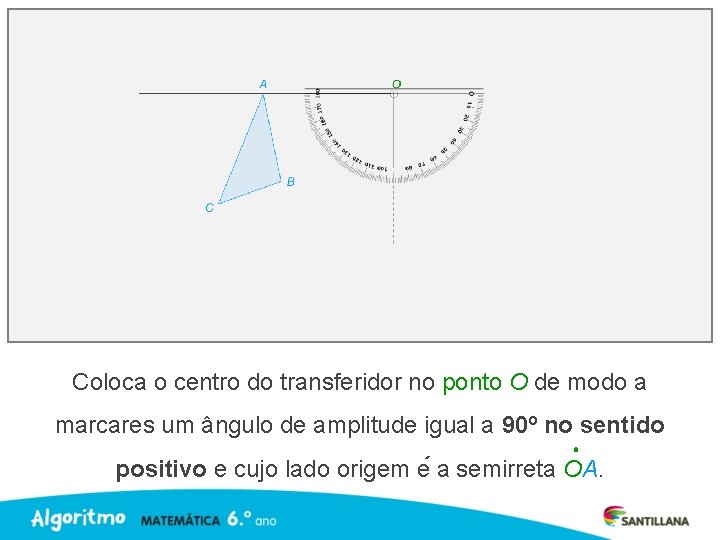
Coloca o centro do transferidor no ponto O de modo a marcares um ângulo de amplitude igual a 90º no sentido positivo e cujo lado origem e a semirreta OA.
![Abre o compasso com a medida do comprimento do segmento OA Abre o compasso com a medida do comprimento do segmento [OA].](https://slidetodoc.com/presentation_image_h2/828c6214e3928027cef0e524fa5ca5ae/image-22.jpg)
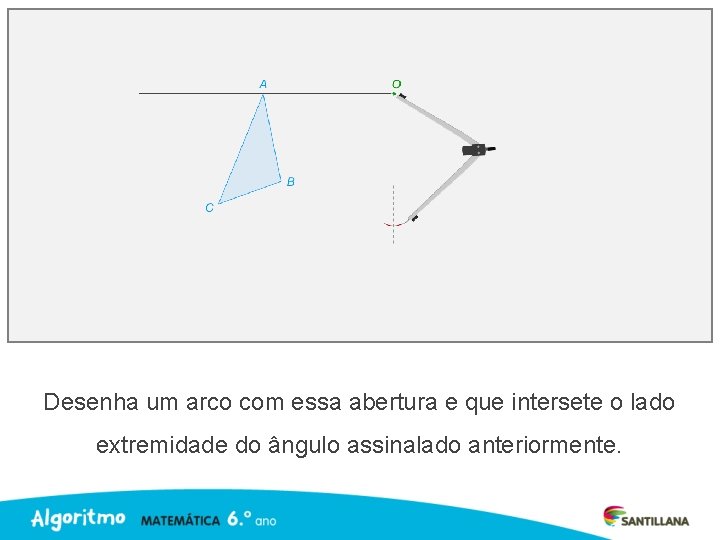
Abre o compasso com a medida do comprimento do segmento [OA].

Desenha um arco com essa abertura e que intersete o lado extremidade do ângulo assinalado anteriormente.

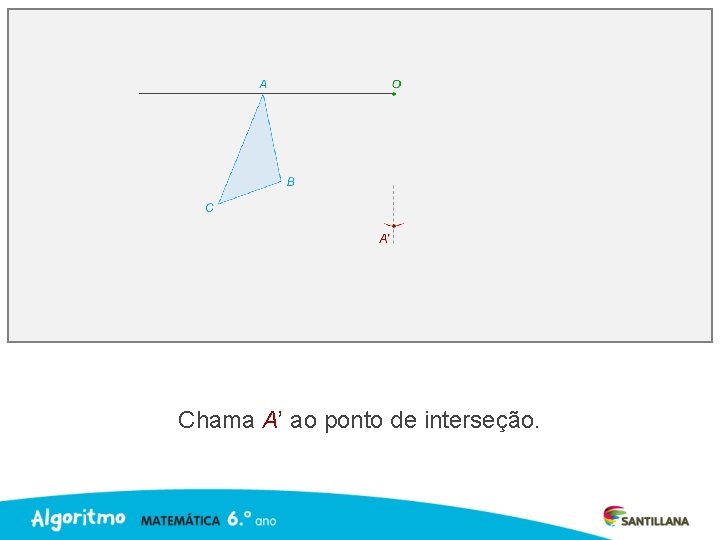
Chama A’ ao ponto de interseção.

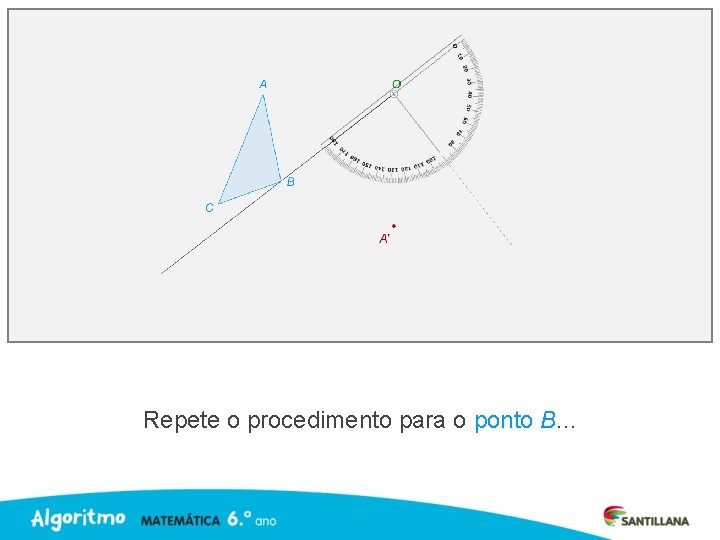
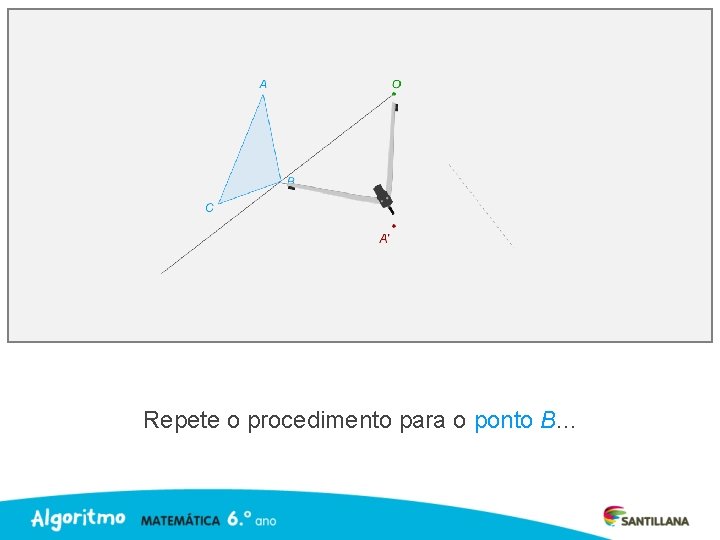
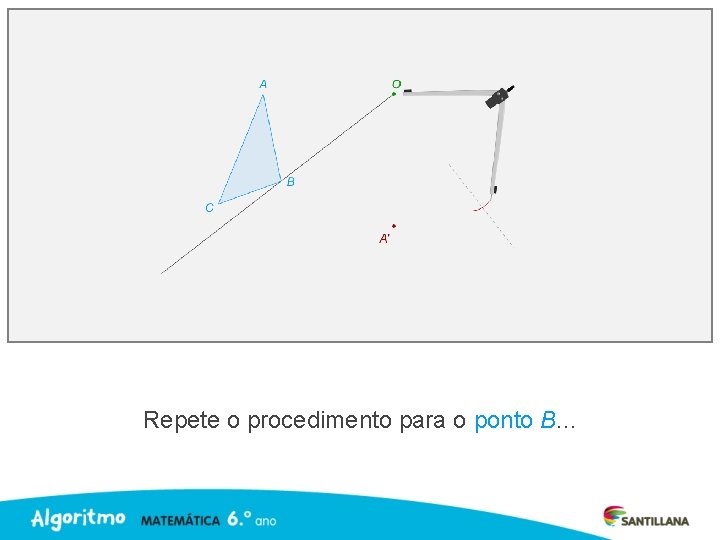
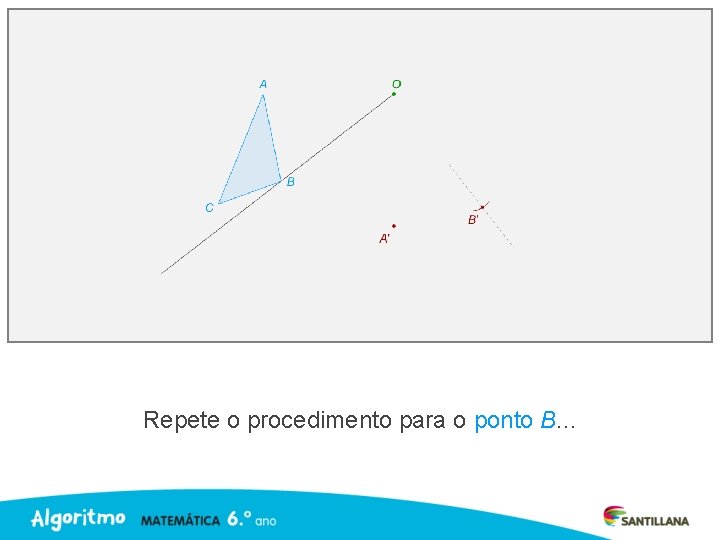
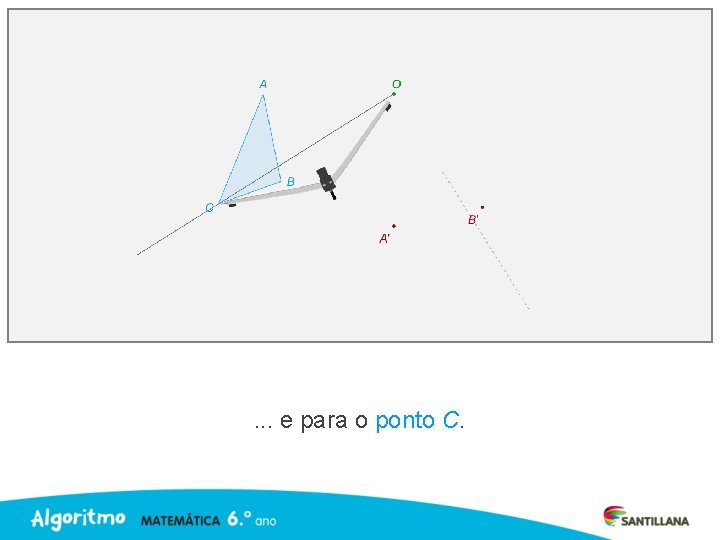
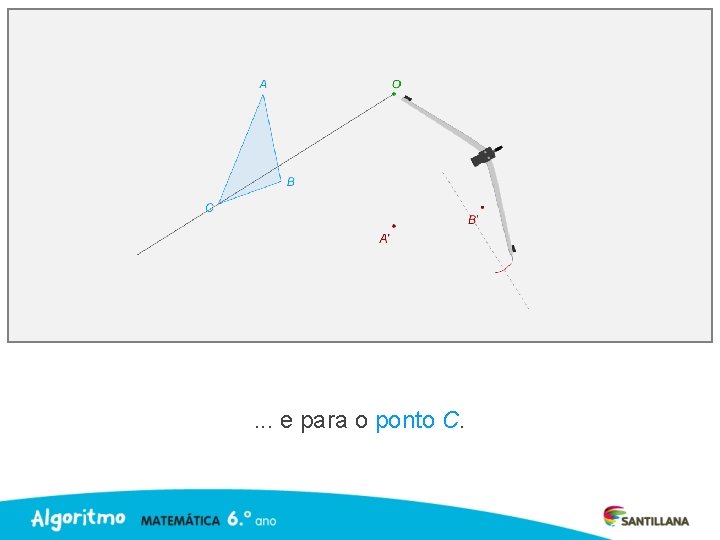
Repete o procedimento para o ponto B. . .

Repete o procedimento para o ponto B. . .

Repete o procedimento para o ponto B. . .

Repete o procedimento para o ponto B. . .

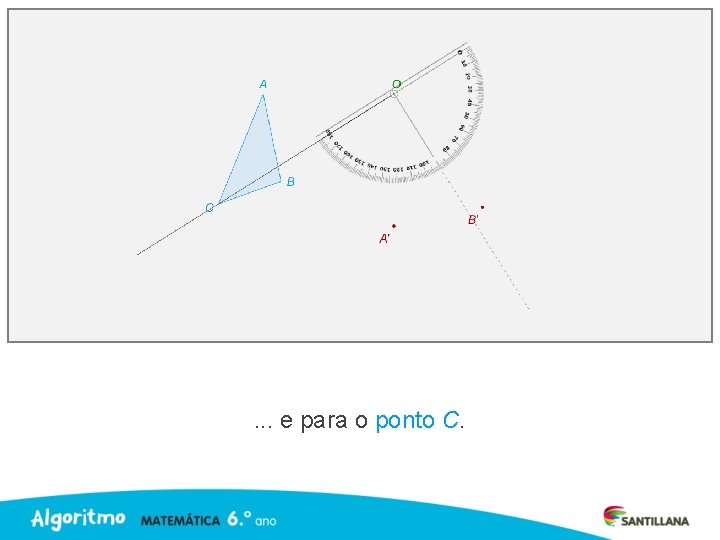
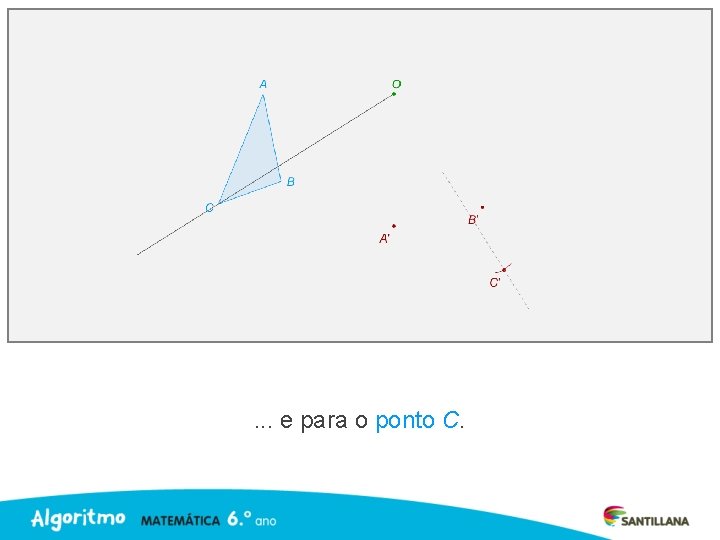
. . . e para o ponto C.

. . . e para o ponto C.

. . . e para o ponto C.

. . . e para o ponto C.

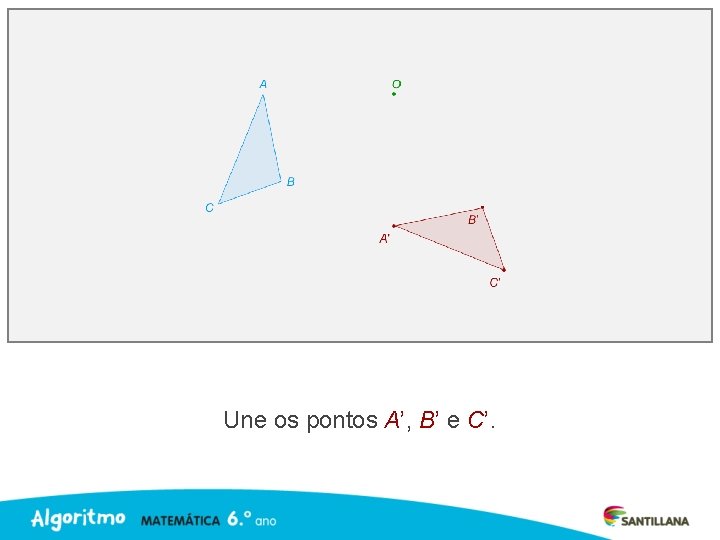
Une os pontos A’, B’ e C’.
![O triângulo ABC resulta da rotação de centro em O e ângulo 90º no O triângulo [A’B’C’] resulta da rotação de centro em O e ângulo 90º no](https://slidetodoc.com/presentation_image_h2/828c6214e3928027cef0e524fa5ca5ae/image-34.jpg)
O triângulo [A’B’C’] resulta da rotação de centro em O e ângulo 90º no sentido positivo do triângulo [ABC].

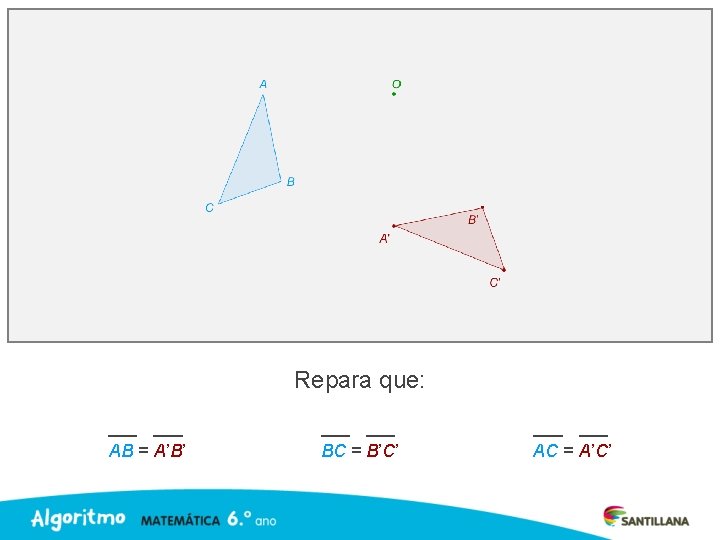
Repara que: AB = A’B’ BC = B’C’ AC = A’C’

Uma rotação preserva distâncias entre os pontos, pelo que e uma isometria.
![Repara que Pelo critério LLL os triângulos ABC e ABC são iguais logo as Repara que: Pelo critério LLL, os triângulos [ABC] e [A’B’C’] são iguais, logo, as](https://slidetodoc.com/presentation_image_h2/828c6214e3928027cef0e524fa5ca5ae/image-37.jpg)
Repara que: Pelo critério LLL, os triângulos [ABC] e [A’B’C’] são iguais, logo, as amplitudes dos ângulos internos dos triângulos também são iguais.

Uma rotação preserva a amplitude de ângulos.
 Isometrias exemplos
Isometrias exemplos Propriedades das isometrias
Propriedades das isometrias Isometrias
Isometrias Diferencia entre gran plano general y plano general
Diferencia entre gran plano general y plano general Momento
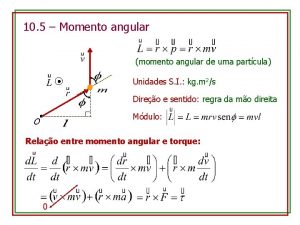
Momento Massa atômica
Massa atômica Unidade caloria
Unidade caloria Igreja nova oeiras
Igreja nova oeiras Sobre o sistema
Sobre o sistema Unidade de ensino superior dom bosco
Unidade de ensino superior dom bosco Unidades de pressão
Unidades de pressão Newton unidade
Newton unidade Competição
Competição Semntica
Semntica Primeira unidade de conservação do brasil
Primeira unidade de conservação do brasil Clula
Clula Na mesa sagrada se faz unidade
Na mesa sagrada se faz unidade Lei de newton
Lei de newton Constante de boltzmann unidade
Constante de boltzmann unidade Simbolo unidade de medida
Simbolo unidade de medida Por nosso senhor jesus cristo na unidade do espirito santo
Por nosso senhor jesus cristo na unidade do espirito santo Unidade de ensino superior dom bosco
Unidade de ensino superior dom bosco Unidade central de processamento
Unidade central de processamento Unidade de medida
Unidade de medida Tkm unidade de medida
Tkm unidade de medida Desarrollo sostenible en nuestra familia y comunidad
Desarrollo sostenible en nuestra familia y comunidad Professor raphael carvalho
Professor raphael carvalho Reta aposta
Reta aposta Keratorefractive surgery ppt
Keratorefractive surgery ppt Como calcular plano alimentar
Como calcular plano alimentar Plano de ação mmr
Plano de ação mmr Plano de nivelamento pei
Plano de nivelamento pei Plano cartesiano
Plano cartesiano Plano de ensino anhanguera
Plano de ensino anhanguera Ventajas de la normalizacion en dibujo tecnico
Ventajas de la normalizacion en dibujo tecnico Etapas de plano de marketing
Etapas de plano de marketing Baby predental
Baby predental Sistema 2
Sistema 2 Planos regionais de ordenamento florestal
Planos regionais de ordenamento florestal