Isometrias Isometrias Isometria uma palavra de origem grega














- Slides: 38

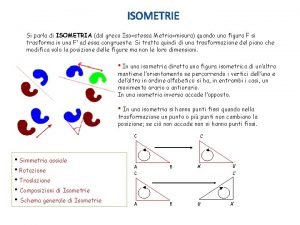
Isometrias.

Isometrias Isometria é uma palavra de origem grega Isos = igual metria = medida

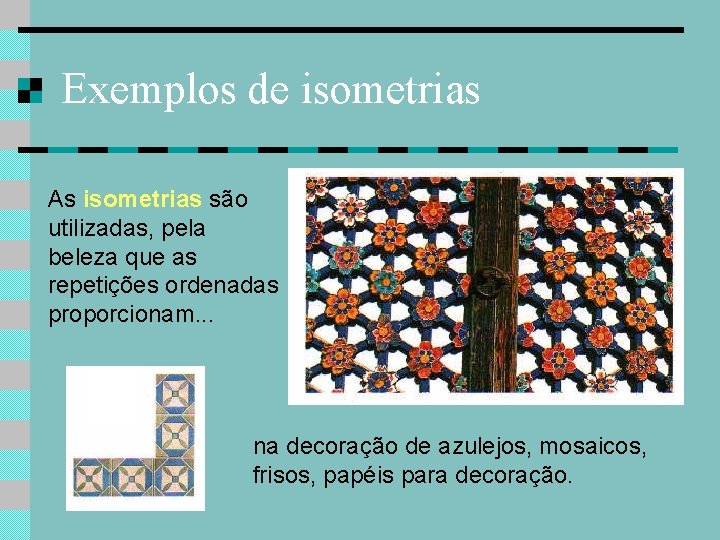
Exemplos de isometrias As isometrias são utilizadas, pela beleza que as repetições ordenadas proporcionam. . . na decoração de azulejos, mosaicos, frisos, papéis para decoração.

Isometrias Mas afinal, como podemos nós obter isometrias?

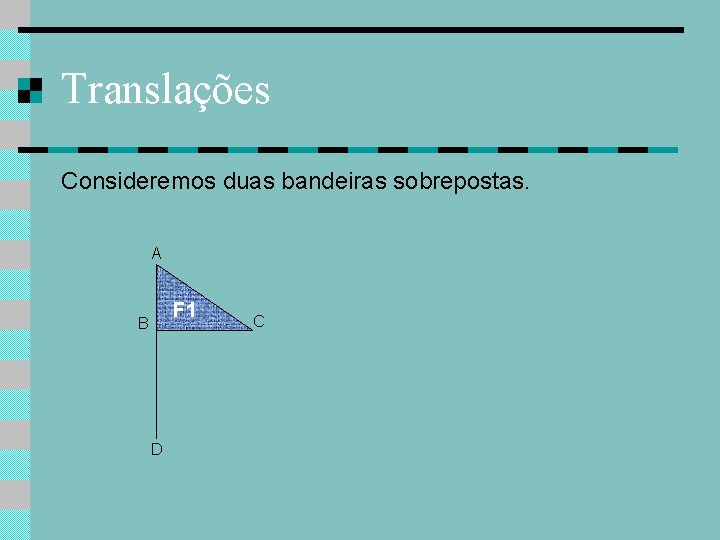
Translações Consideremos duas bandeiras sobrepostas.

Translações Consideremos duas bandeiras sobrepostas. A F 1 B D C

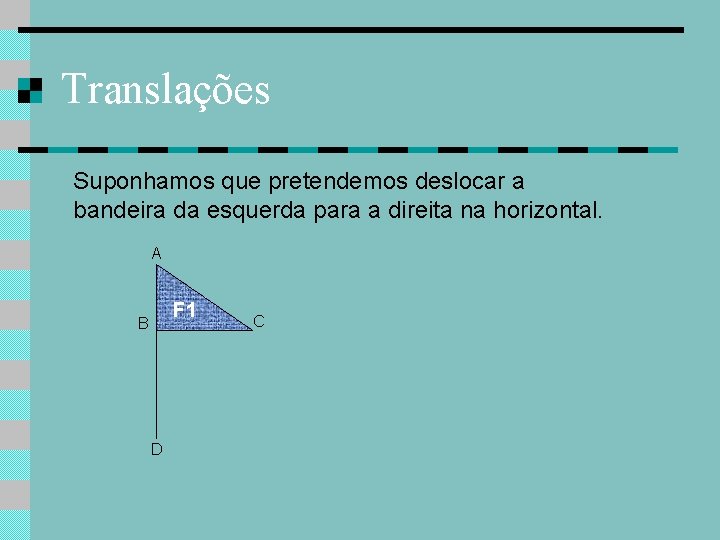
Translações Suponhamos que pretendemos deslocar a bandeira da esquerda para a direita na horizontal. A F 1 B D C

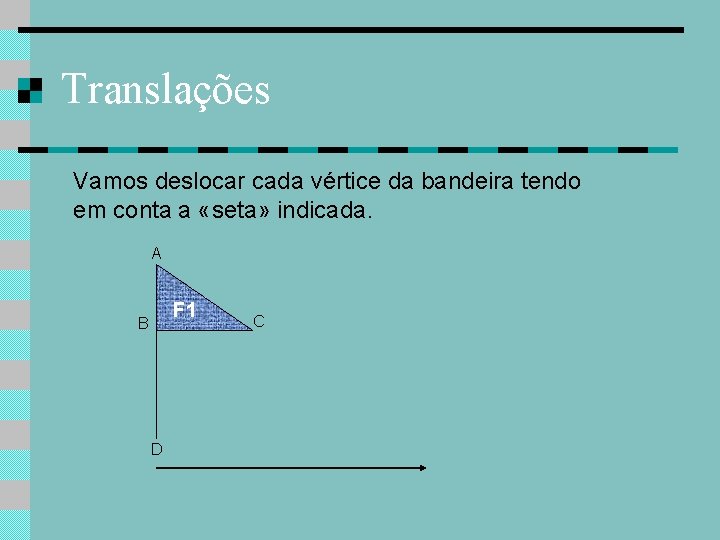
Translações Vamos deslocar cada vértice da bandeira tendo em conta a «seta» indicada. A F 1 B D C

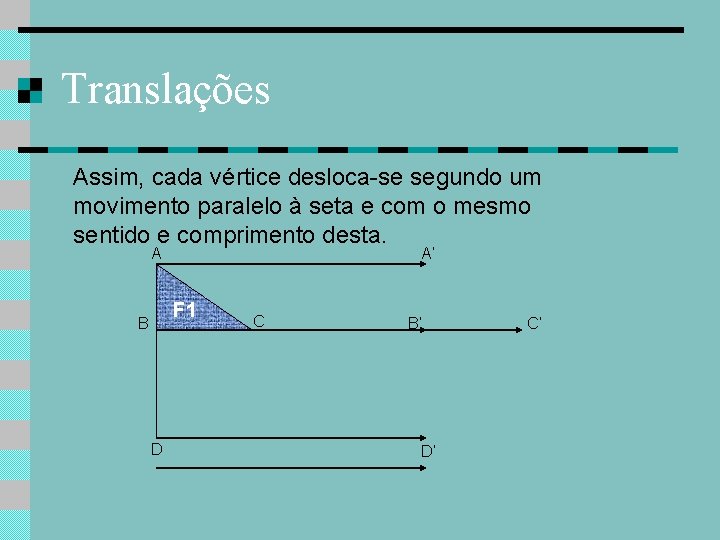
Translações Assim, cada vértice desloca-se segundo um movimento paralelo à seta e com o mesmo sentido e comprimento desta. A A’ F 1 B D C B’ D’ C’

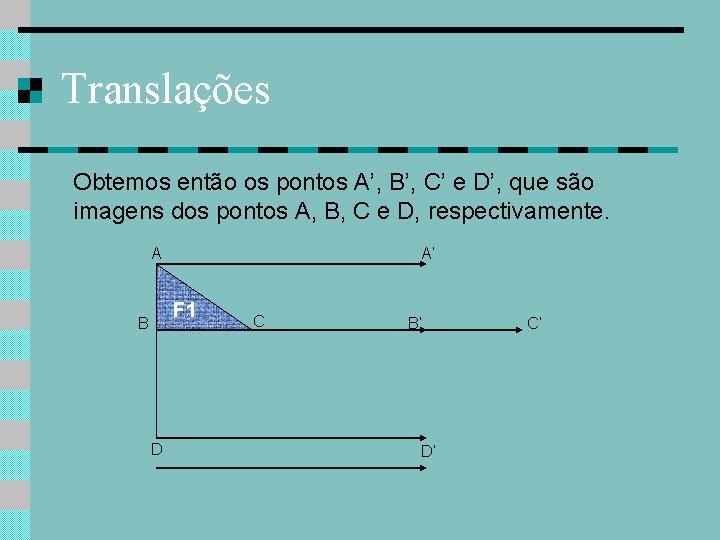
Translações Obtemos então os pontos A’, B’, C’ e D’, que são imagens dos pontos A, B, C e D, respectivamente. A A’ F 1 B D C B’ D’ C’

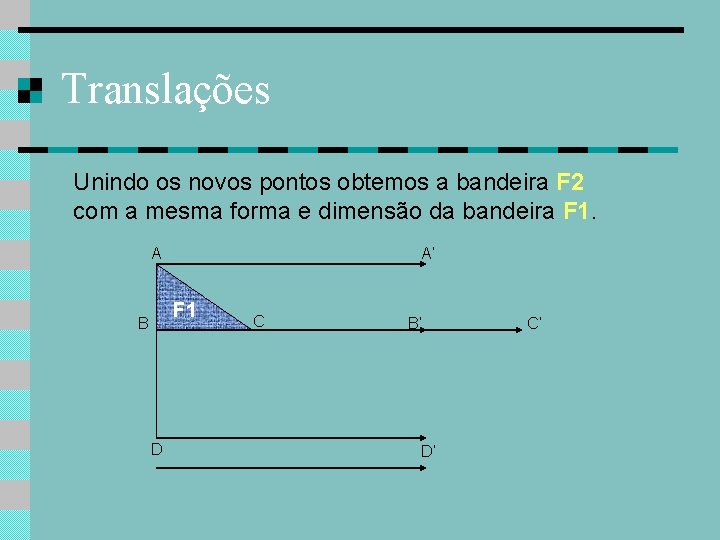
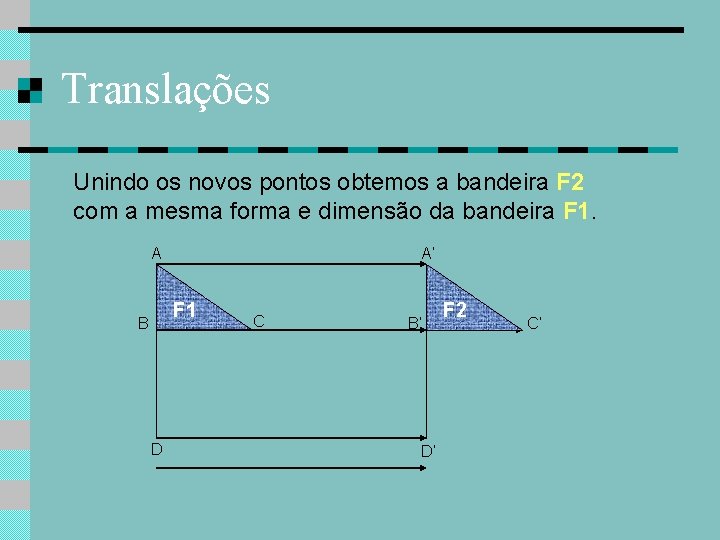
Translações Unindo os novos pontos obtemos a bandeira F 2 com a mesma forma e dimensão da bandeira F 1. A A’ F 1 B D C B’ D’ C’

Translações Unindo os novos pontos obtemos a bandeira F 2 com a mesma forma e dimensão da bandeira F 1. A A’ F 1 B D C B’ D’ F 2 C’

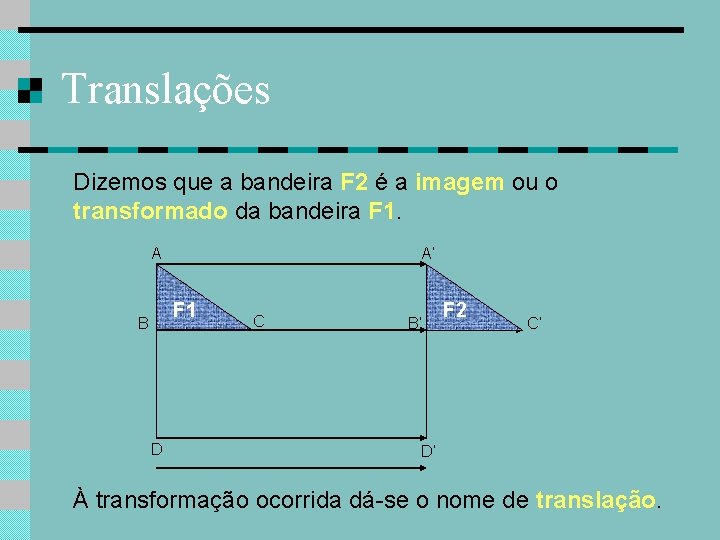
Translações Dizemos que a bandeira F 2 é a imagem ou o transformado da bandeira F 1. A A’ F 1 B D C B’ F 2 C’ D’ À transformação ocorrida dá-se o nome de translação.

Vectores Numa seta podemos considerar três características: a direcção, o sentido e o comprimento. Desta forma, dizemos que temos definido um vector.

Vectores À translação anterior temos assim associado o vector que nos permite passar da figura inicial, a bandeira F 1 para a nova bandeira F 2. C C’

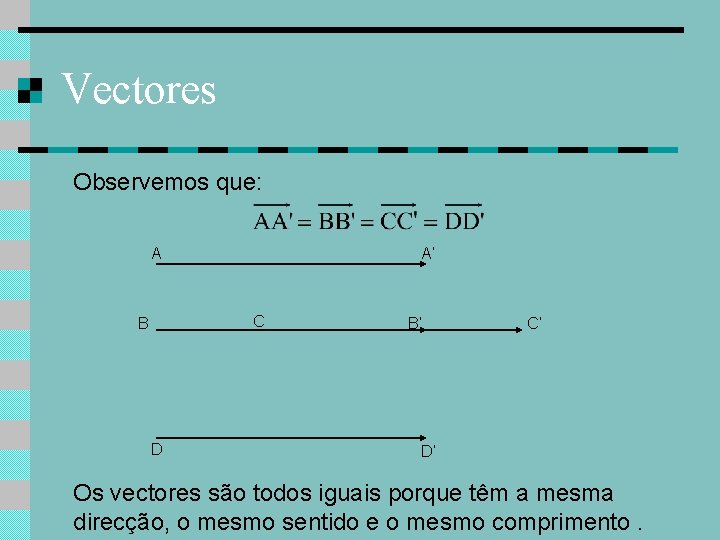
Vectores Observemos que: A A’ C B D B’ C’ D’ Os vectores são todos iguais porque têm a mesma direcção, o mesmo sentido e o mesmo comprimento.

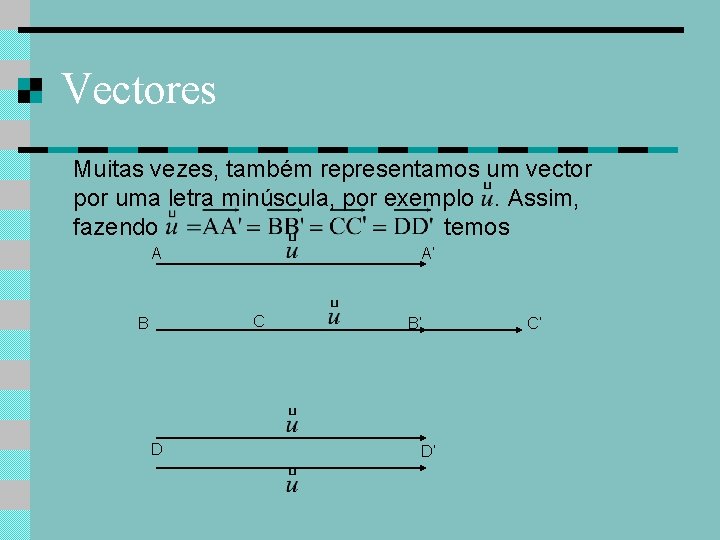
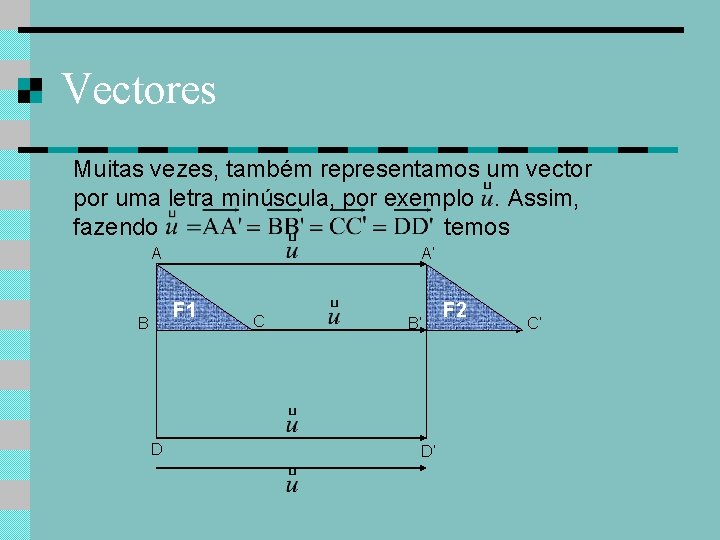
Vectores Muitas vezes, também representamos um vector por uma letra minúscula, por exemplo. Assim, fazendo temos A A’ C B D B’ D’ C’

Vectores Muitas vezes, também representamos um vector por uma letra minúscula, por exemplo. Assim, fazendo temos A A’ F 1 B D C B’ D’ F 2 C’

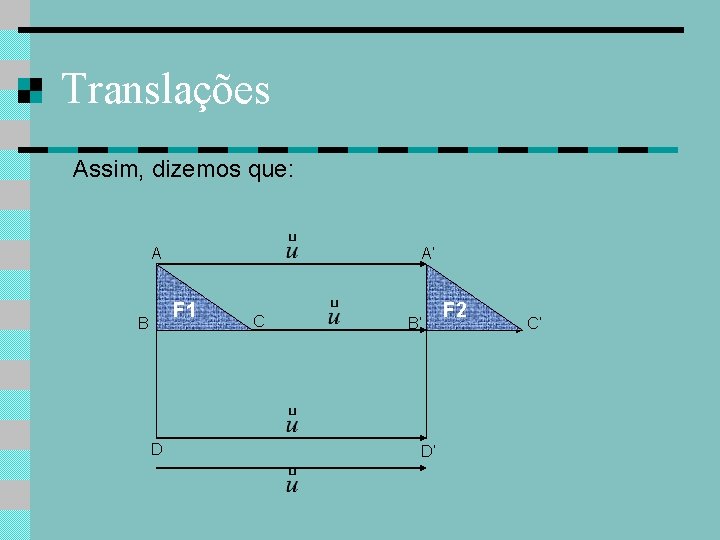
Translações Assim, dizemos que: A A’ F 1 B D C B’ D’ F 2 C’

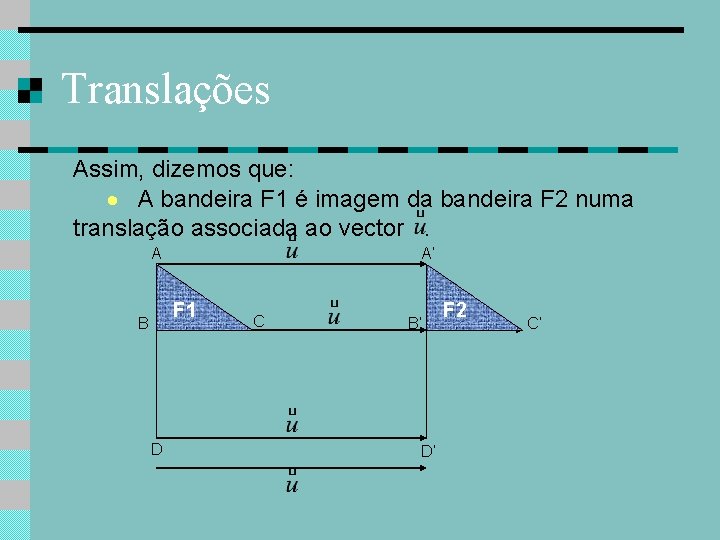
Translações Assim, dizemos que: A bandeira F 1 é imagem da bandeira F 2 numa translação associada ao vector. A A’ F 1 B D C B’ D’ F 2 C’

Propriedades das translações Tal como nas rotações A imagem de um segmento de recta é um segmento de recta geometricamente igual Exemplo: [AD] [A’D’] A imagem de um ângulo é um ângulo geometricamente igual. Exemplo: CAB C’A’B’ Estas propriedades são comuns a todas as translações.

Simetrias axiais Consideremos uma bandeira F 1.

Simetrias axiais Consideremos uma bandeira F 1. A F 1 B D C

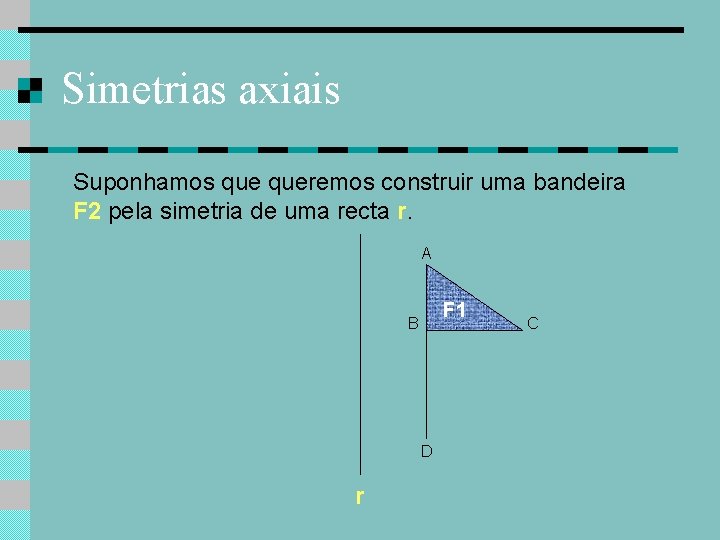
Simetrias axiais Suponhamos queremos construir uma bandeira F 2 pela simetria de uma recta r. A F 1 B D r C

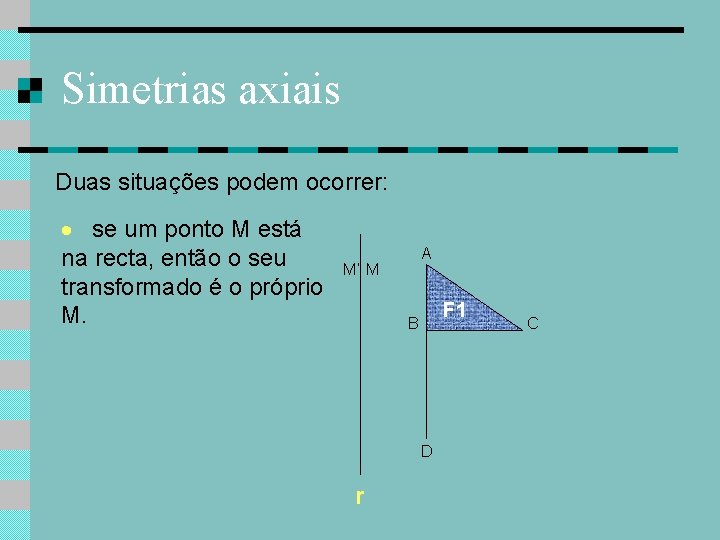
Simetrias axiais Duas situações podem ocorrer: se um ponto M está na recta, então o seu transformado é o próprio M. A M’ M F 1 B D r C

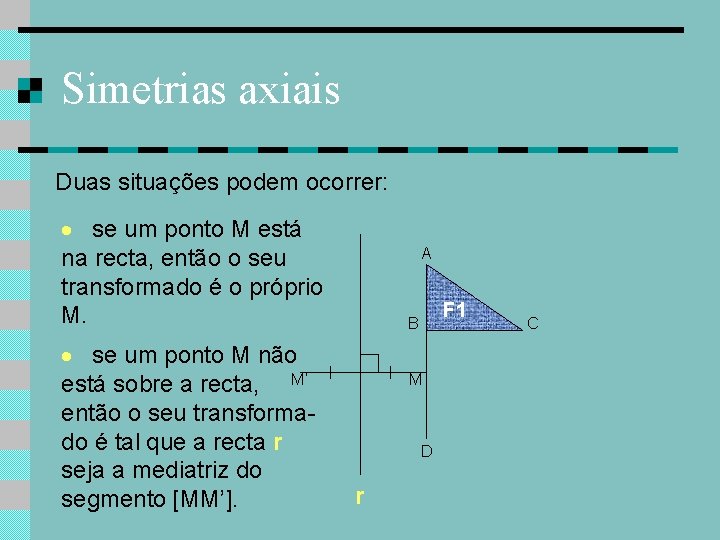
Simetrias axiais Duas situações podem ocorrer: se um ponto M está na recta, então o seu transformado é o próprio M. se um ponto M não está sobre a recta, M’ então o seu transformado é tal que a recta r seja a mediatriz do segmento [MM’]. A F 1 B M D r C

Simetrias axiais Duas situações podem ocorrer: se um ponto M está na recta, então o seu transformado é o próprio M. se um ponto M não está sobre a recta, M’ então o seu transformado é tal que a recta r seja a mediatriz do segmento [MM’]. A F 1 B M D r C

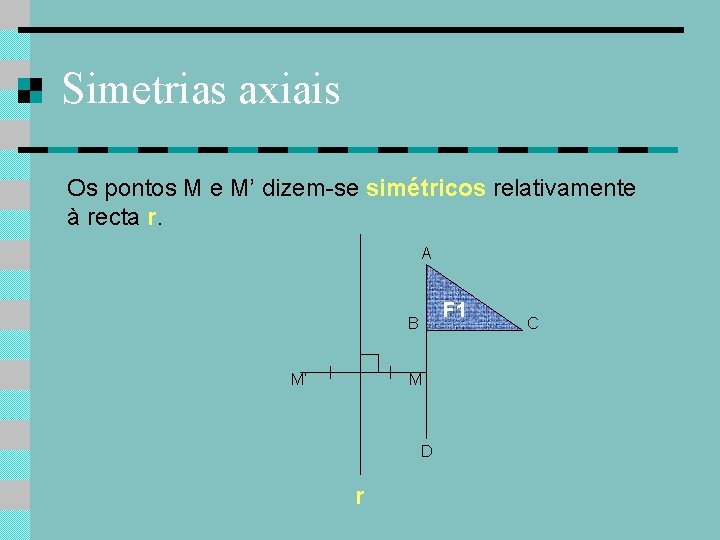
Simetrias axiais Os pontos M e M’ dizem-se simétricos relativamente à recta r. A F 1 B M’ M D r C

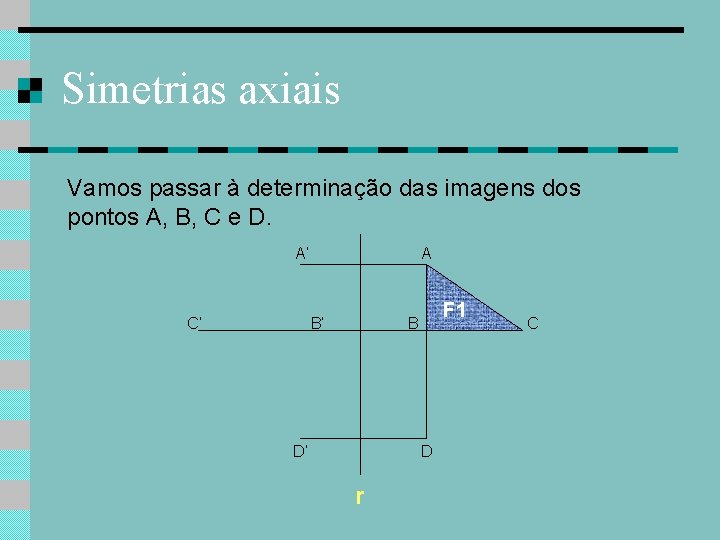
Simetrias axiais Vamos passar à determinação das imagens dos pontos A, B, C e D. A’ C’ A B’ F 1 B D’ D r C

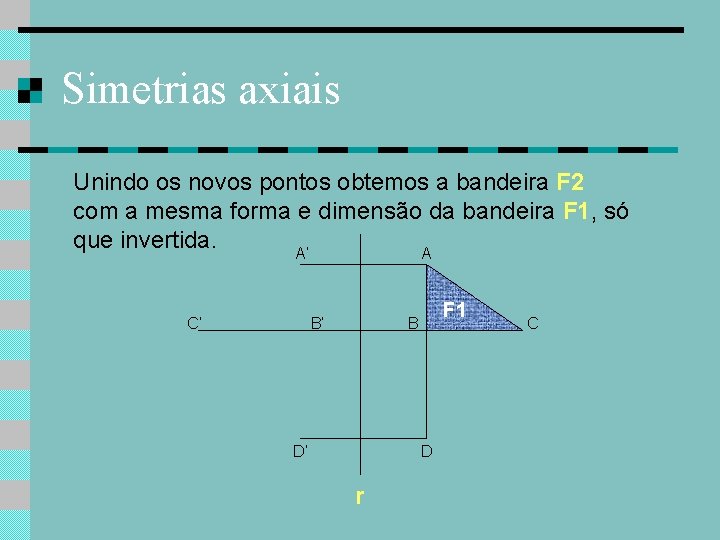
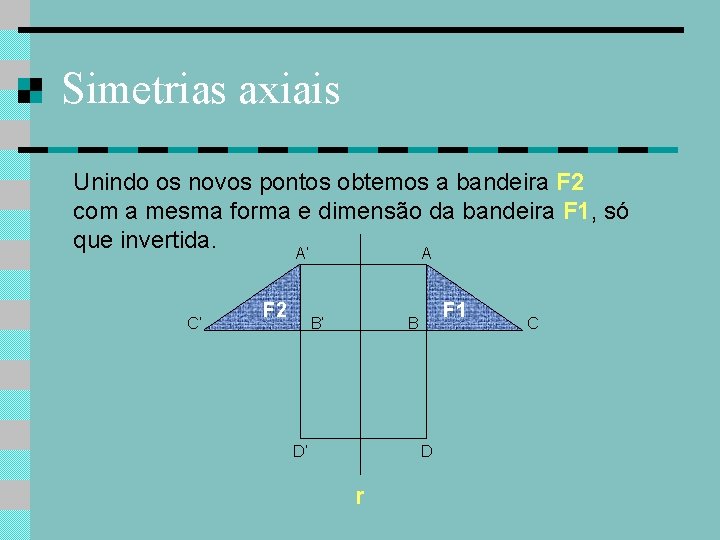
Simetrias axiais Unindo os novos pontos obtemos a bandeira F 2 com a mesma forma e dimensão da bandeira F 1, só que invertida. A’ A C’ B’ F 1 B D’ D r C

Simetrias axiais Unindo os novos pontos obtemos a bandeira F 2 com a mesma forma e dimensão da bandeira F 1, só que invertida. A’ A C’ F 2 B’ F 1 B D’ D r C

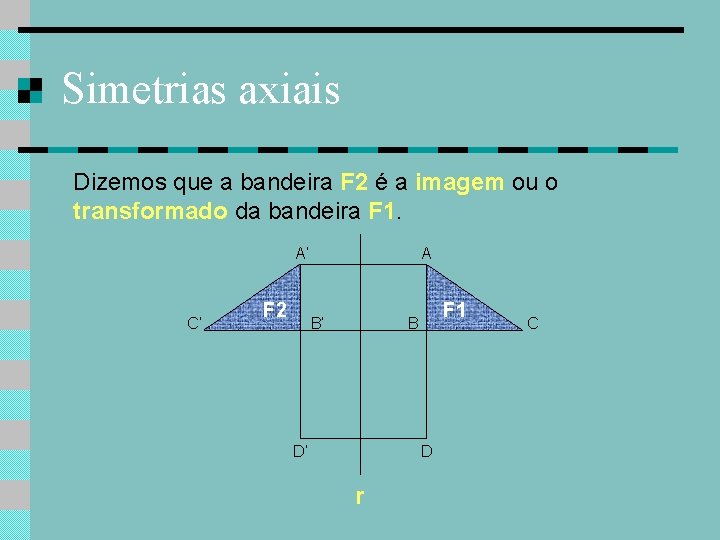
Simetrias axiais Dizemos que a bandeira F 2 é a imagem ou o transformado da bandeira F 1. A’ C’ F 2 A B’ F 1 B D’ D r C

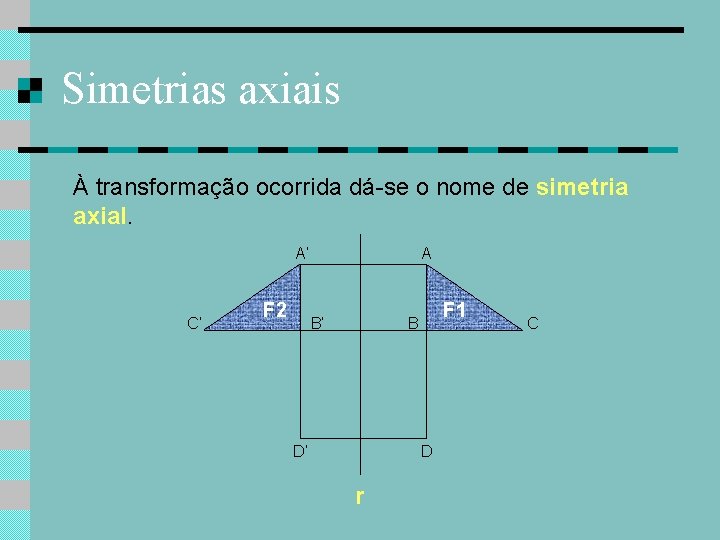
Simetrias axiais À transformação ocorrida dá-se o nome de simetria axial. A’ C’ F 2 A B’ F 1 B D’ D r C

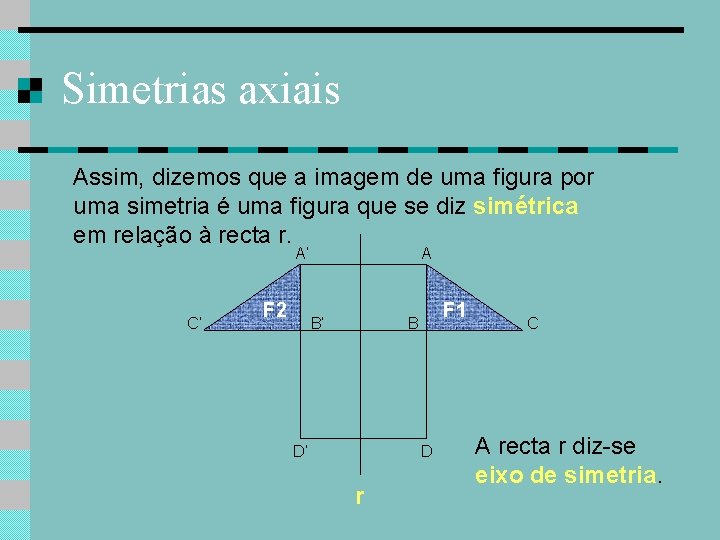
Simetrias axiais Assim, dizemos que a imagem de uma figura por uma simetria é uma figura que se diz simétrica em relação à recta r. A’ C’ F 2 A B’ F 1 B D’ D r C A recta r diz-se eixo de simetria.

Propriedades das simetrias axiais Então, A imagem de um segmento de recta é um segmento de recta geometricamente igual Exemplo: [AD] [A’D’] A imagem de um ângulo é um ângulo geometricamente igual, mas orientado em sentido contrário. Exemplo: CAB C’A’B’ Estas propriedades são comuns a todas as simetrias axiais.

Comparação das propriedades das isometrias Nas rotações e nas translações a figura resultante tem o mesmo sentido. Nas simetrias axiais a figura aparece invertida. As rotações e as translações mantém o sentido dos ângulos. As simetrias axiais invertem o sentido dos ângulos. As rotações, translações e simetrias axiais mantém a medida de comprimento dos segmentos As rotações, translações e simetrias axiais mantém a medida de amplitude dos ângulos.

Classificação das isometrias Estas características levam-nos a classificar as isometrias em dois tipos: Isometrias positivas mantém o sentido dos ângulos orientados Exemplo: Rotações, translações. Isometrias negativas invertem o sentido dos ângulos orientados Exemplo: Simetrias axiais.

Isometrias Mas afinal o que são isometrias? Uma Isometria é uma transformação geométrica em que são conservados as medidas de comprimento dos segmentos de recta e as medidas de amplitude dos ângulos.
 Grego eletricidade
Grego eletricidade Uma flecha lançada uma palavra dita
Uma flecha lançada uma palavra dita Fluuig
Fluuig Origem da palavra comunidade
Origem da palavra comunidade Qual a origem da palavra filosofia
Qual a origem da palavra filosofia A filosofia como conhecemos hoje
A filosofia como conhecemos hoje Isometrias
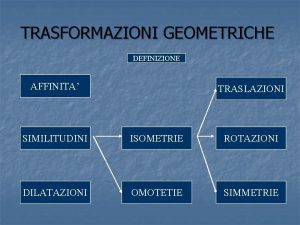
Isometrias Transformaes
Transformaes Isometrias
Isometrias Isometria
Isometria Isomeria ottica
Isomeria ottica Isometria geometria
Isometria geometria Isometria central
Isometria central Glissoriflessione
Glissoriflessione Omotetia e similitudine
Omotetia e similitudine Isometria etimologia
Isometria etimologia Isometria rotação
Isometria rotação Isometria
Isometria Como pesquisar a origem de uma imagem
Como pesquisar a origem de uma imagem Formam ou formão
Formam ou formão Liberdade é uma palavra que o sonho humano alimenta
Liberdade é uma palavra que o sonho humano alimenta Palavras hibridas
Palavras hibridas Diaspora grega
Diaspora grega Grega faulla
Grega faulla Diaspora grega
Diaspora grega Nano letra grega
Nano letra grega Diaspora grega
Diaspora grega Kouros arte grega
Kouros arte grega Nascimento da polis
Nascimento da polis Ponto roseta sutura
Ponto roseta sutura Teatro etimologia
Teatro etimologia Habitavam os campos e bosques na mitologia grega
Habitavam os campos e bosques na mitologia grega Lilian origem
Lilian origem Uma cultura aberta à cidade
Uma cultura aberta à cidade Questes
Questes Tau minusculo
Tau minusculo Diversidade de plantas na terra
Diversidade de plantas na terra Galinha azulzinha
Galinha azulzinha Concava e convexa
Concava e convexa