Geometria Reflexo 1 ciclo Reflexo rotao e translao

Geometria Reflexão (1º ciclo) Reflexão, rotação e translação (2º ciclo) Isometrias (3º ciclo) Margarida Oliveira guidacoliveira@gmail. com Isilda Pedro isildapedro@netcabo. pt

Tópicos e objectivos específicos (PMEB) � Reflexão (1º ciclo) - 1º e 2º anos: • Identificar figuras simétricas em relação a um eixo • Desenhar figuras simétricas relativas a um eixo horizontal ou vertical - 3º e 4º anos: • Identificar eixos de simetria de figuras • Construir frisos e identificar simetrias • Construir pavimentações com polígonos

Tópicos e objectivos específicos (PMEB) � Reflexão, rotação e translação (2º ciclo) - Noção e propriedades da reflexão, da rotação e da translação - Simetrias axial e rotacional � Isometrias (3º ciclo) -Translação associada a um vector - Propriedades das isometrias

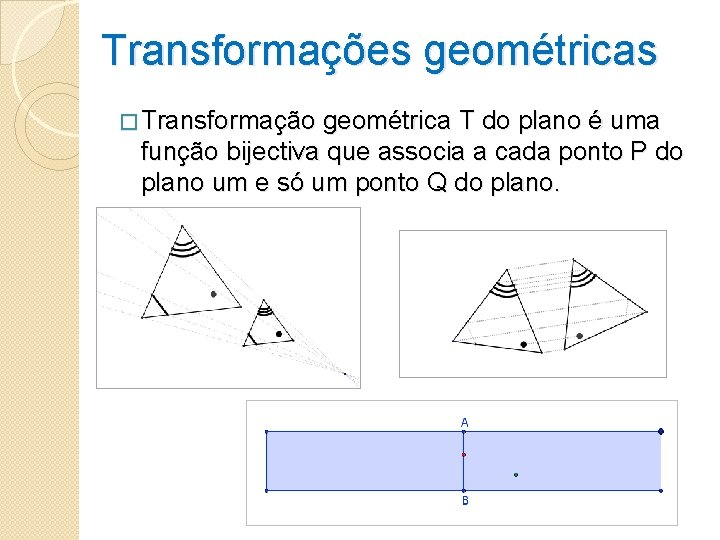
Transformações geométricas � Transformação geométrica T do plano é uma função bijectiva que associa a cada ponto P do plano um e só um ponto Q do plano.

Isometria É uma transformação geométrica em que para quaisquer dois pontos A e B, dist(A, B) = dist(A’, B’) em que A’ e B’ são os transformados de A e B respectivamente

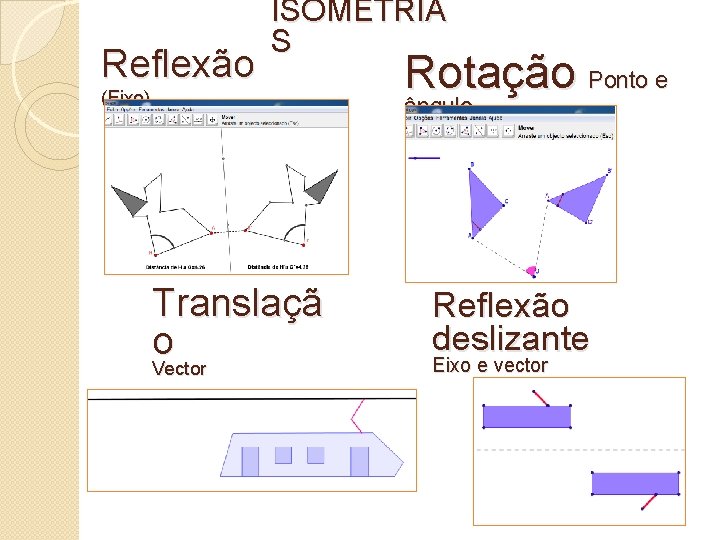
Reflexão ISOMETRIA S (Eixo) Rotação Ponto e ângulo Translaçã o Vector Reflexão deslizante Eixo e vector

Simetria s

Simetria s �A simetria é uma característica que pode ser observada em algumas formas geométricas. (wikipédia) �A simetria na Natureza é um fenómeno único e fascinante. (http: //www. educ. fc. ul. pt/icm 2002/icm 203/geometria. htm) � Esta ideia surge naturalmente ao espírito humano, remetendo-o para um equilíbrio e proporção, padrão e regularidade, harmonia e beleza, ordem e perfeição. (http: //www. educ. fc. ul. pt/icm 2002/icm 203/geometria. htm)

Definição matemática do conceito de simetria �Dada uma figura plana F, chama-se simetria de F a toda a isometria do plano que deixe F invariante. Uma entidade é considerada invariante sob um conjunto de transformações se a imagem transformada da entidade é indistinguível da entidade original.

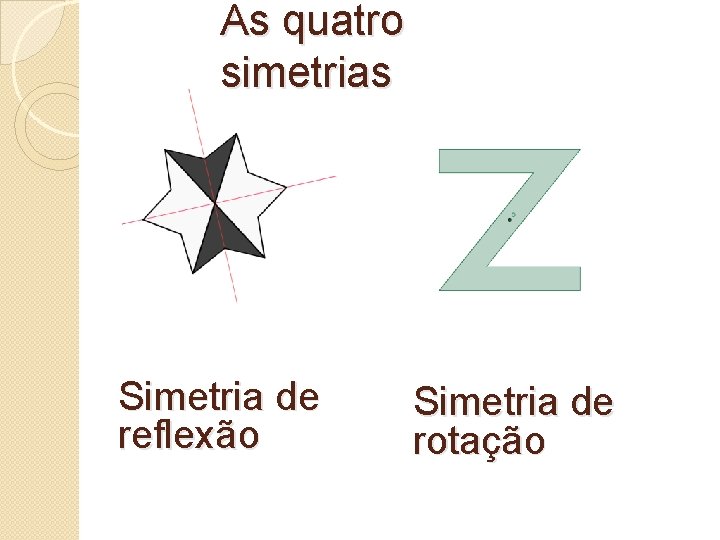
As quatro simetrias Simetria de reflexão Simetria de rotação

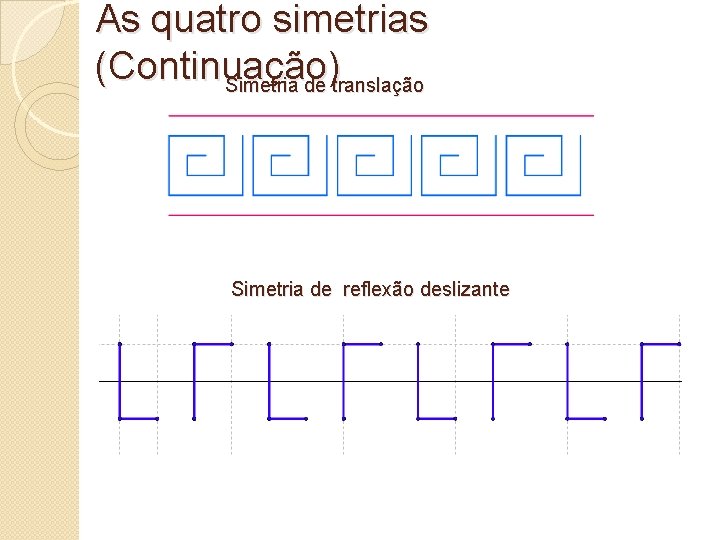
As quatro simetrias (Continuação) Simetria de translação Simetria de reflexão deslizante

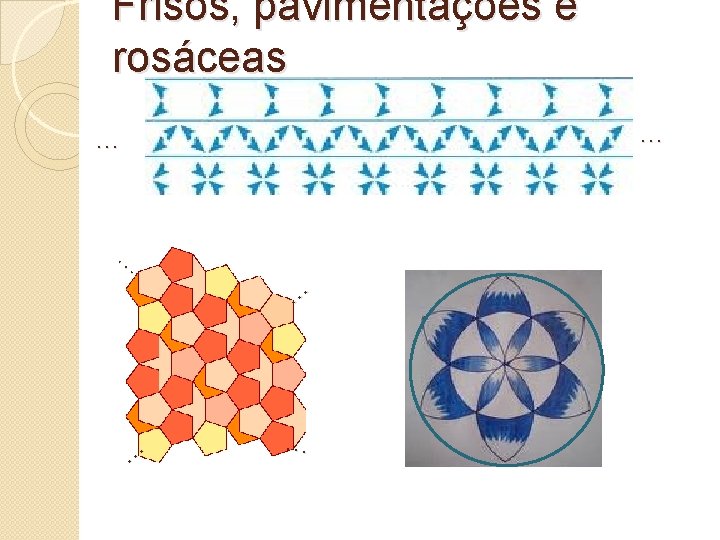
Frisos, pavimentações e rosáceas … … …

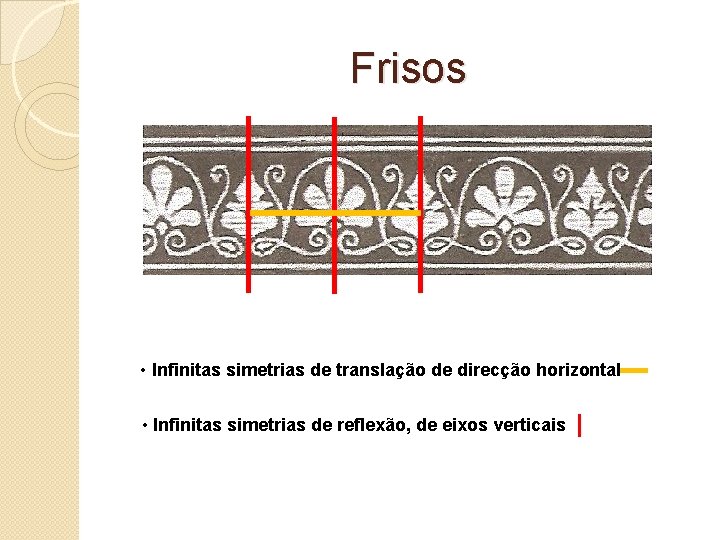
Frisos • Infinitas simetrias de translação de direcção horizontal • Infinitas simetrias de reflexão, de eixos verticais |

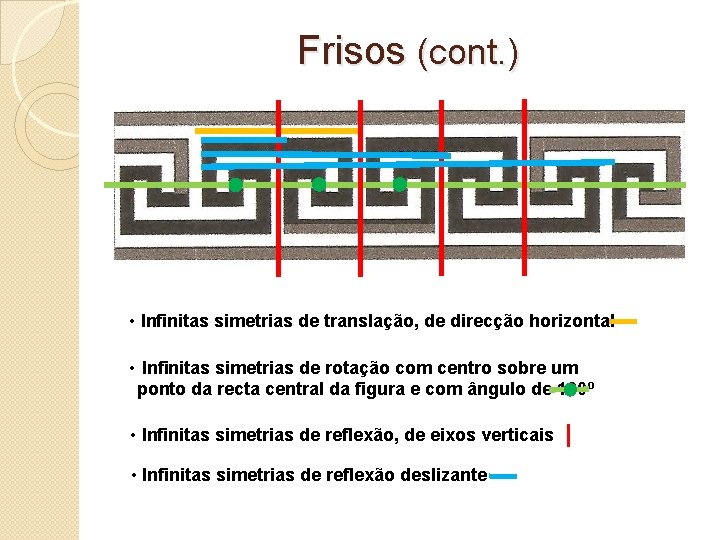
Frisos (cont. ) • Infinitas simetrias de translação, de direcção horizontal • Infinitas simetrias de rotação com centro sobre um ponto da recta central da figura e com ângulo de 180º • Infinitas simetrias de reflexão, de eixos verticais • Infinitas simetrias de reflexão deslizante |

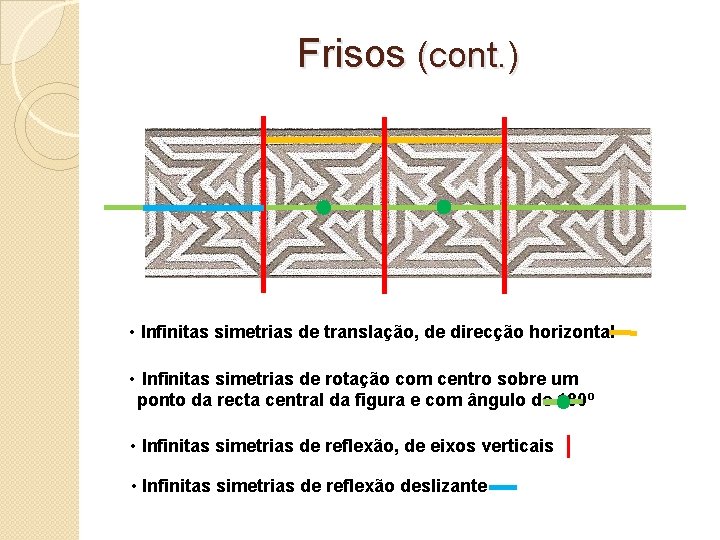
Frisos (cont. ) • Infinitas simetrias de translação, de direcção horizontal • Infinitas simetrias de rotação com centro sobre um ponto da recta central da figura e com ângulo de 180º • Infinitas simetrias de reflexão, de eixos verticais • Infinitas simetrias de reflexão deslizante |

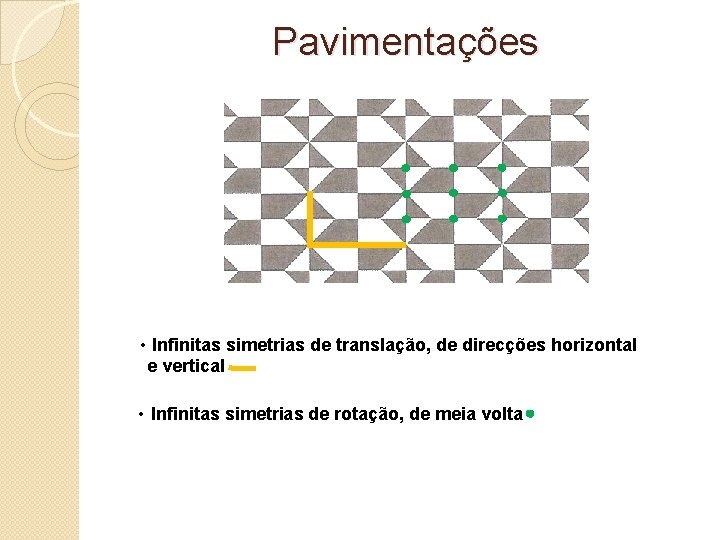
Pavimentações • Infinitas simetrias de translação, de direcções horizontal e vertical • Infinitas simetrias de rotação, de meia volta

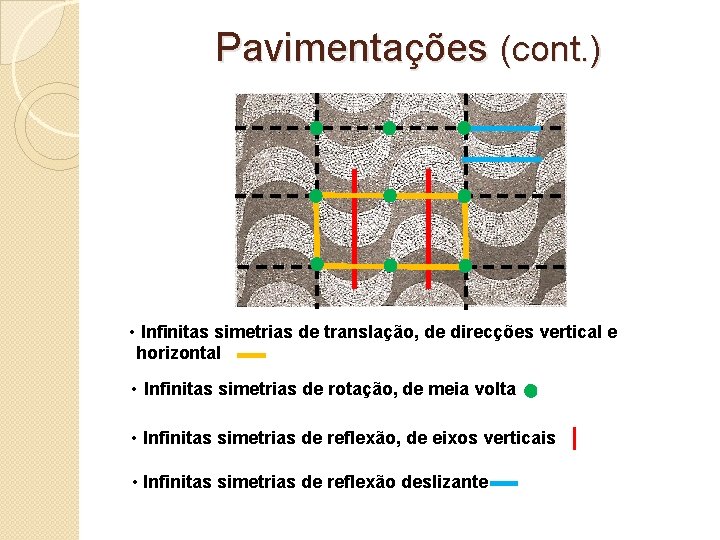
Pavimentações (cont. ) • Infinitas simetrias de translação, de direcções vertical e horizontal • Infinitas simetrias de rotação, de meia volta • Infinitas simetrias de reflexão, de eixos verticais • Infinitas simetrias de reflexão deslizante |

Rosáceas • 6 simetrias de rotação com centro no “centro” da figura. As rotações têm ângulos de 60º, 120º, 180º, 240º e 360º. • 6 simetrias de reflexão cujos eixos coincidem com as simetrias de rotação.

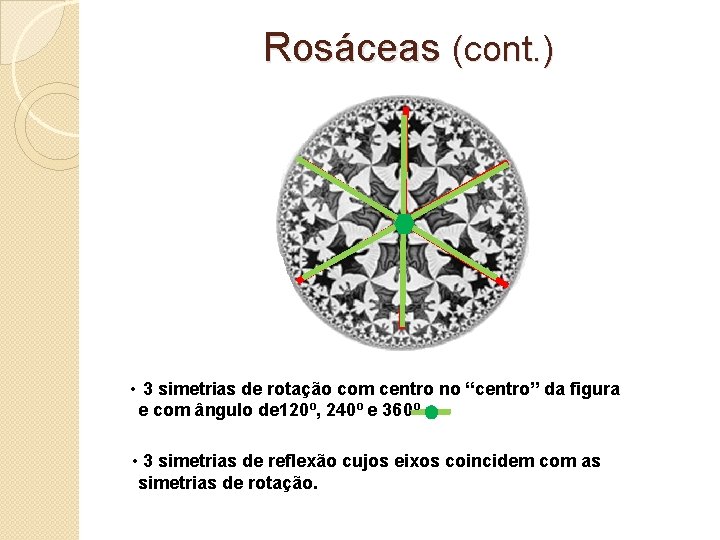
Rosáceas (cont. ) • 3 simetrias de rotação com centro no “centro” da figura e com ângulo de 120º, 240º e 360º • 3 simetrias de reflexão cujos eixos coincidem com as simetrias de rotação.

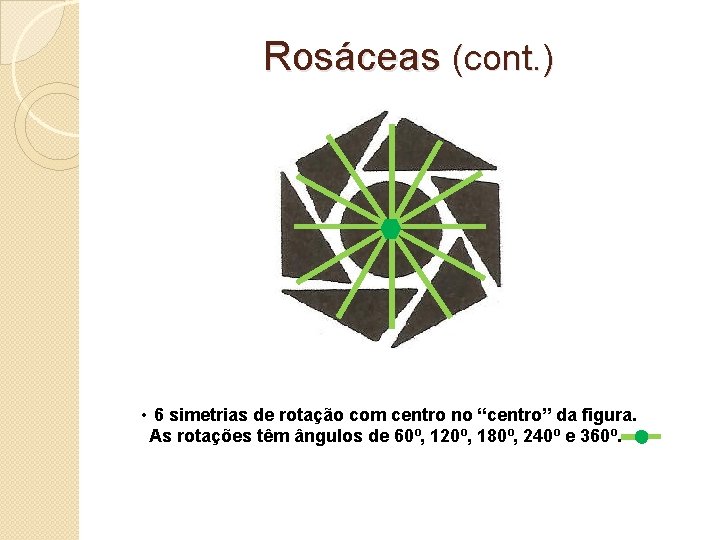
Rosáceas (cont. ) • 6 simetrias de rotação com centro no “centro” da figura. As rotações têm ângulos de 60º, 120º, 180º, 240º e 360º.

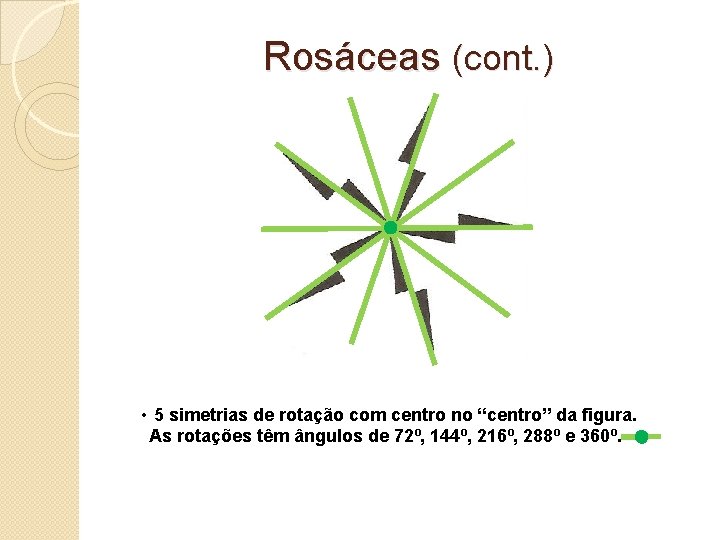
Rosáceas (cont. ) • 5 simetrias de rotação com centro no “centro” da figura. As rotações têm ângulos de 72º, 144º, 216º, 288º e 360º.