Unidad 5 Interpolacin 5 1 Polinomio de interpolacin

Unidad 5. -Interpolación 5. 1 Polinomio de interpolación de Newton. 5. 2 Polinomio de interpolación de Lagrange. 5. 3 Interpolación segmentada. 5. 4 Problemas de aplicación. Integrantes: Dionicio García Berenice Domínguez Vivar Areli Hernández Pérez Carla Martínez Aguilera Alan Matus Gutiérrez José Eduardo Sastre Hernández Carlos Eduardo Zacarías Montero Jairo Albino

5. 1 Polinomio de interpolación de Newton. � Existe una gran variedad de formas alternativas para expresar una interpolación polinomial. El polinomio de interpolación de Newton en diferencias divididas es una de las formas más populares y útiles.

� Ecuación � Los polinomio: puntos asociados con datos se utilizan para evaluar los coeficientes b 0, b 1, . . , bn. Para un polinomio de nésimo grado se requieren n + 1 puntos: [x 0, f(x 0)], [x 1, f(x 1)], . . , [xn, f(xn)]. Usamos � estos datos y las siguientes ecuaciones para evaluar los coeficientes: � b 0 = f(x 0) � b 1 = f[x 1, x 0] � b 2 = f[x 2, x 1, x 0] �· � bn = f[xn, xn– 1, · · ·, x 1, x 0]

5. 1 Polinomio de interpolación de Newton. � Donde las evaluaciones de la función colocadas entre paréntesis son diferencias divididas finitas. � En forma similar, la n-ésima diferencia dividida finita es

5. 1 Polinomio de interpolación de Newton. � Estas diferencias sirven para evaluar los coeficientes en las ecuaciones, los cuales se sustituirán en la ecuación para obtener el polinomio de interpolación � fn(x) = f(x 0) + (x – x 0) f[x 1, x 0] + (x – x 0)(x – x 1) f[x 2, x 1, x 0] +··+ (x – x 0)(x – x 1)··(x – xn– 1) f[xn, xn– 1, ··, x 0] � que se conoce como polinomio de interpolación de Newton en diferencias divididas.

5. 1 Polinomio de interpolación de Newton. � 3 propiedades para aplicaciones en computadora: � 1. Es posible desarrollar de manera secuencial versiones de grado superior con la adición de un solo término a la ecuación de grado inferior. Al agregar nuevos términos en forma secuencial, podemos determinar cuándo se alcanza un punto de regreso disminuido. � 2. Las diferencias divididas finitas que constituyen los coeficientes del polinomio se pueden calcular eficientemente. Utilizando esta información previamente determinada, los coeficientes se calculan de manera eficiente.

5. 1 Polinomio de interpolación de Newton. � 3. El error estimado incorpora con facilidad en un algoritmo computacional debido a la manera secuencial en la cual se construye la predicción. Todas las características anteriores pueden aprovecharse e incorporarse en un algoritmo general para implementar el polinomio de Newton.

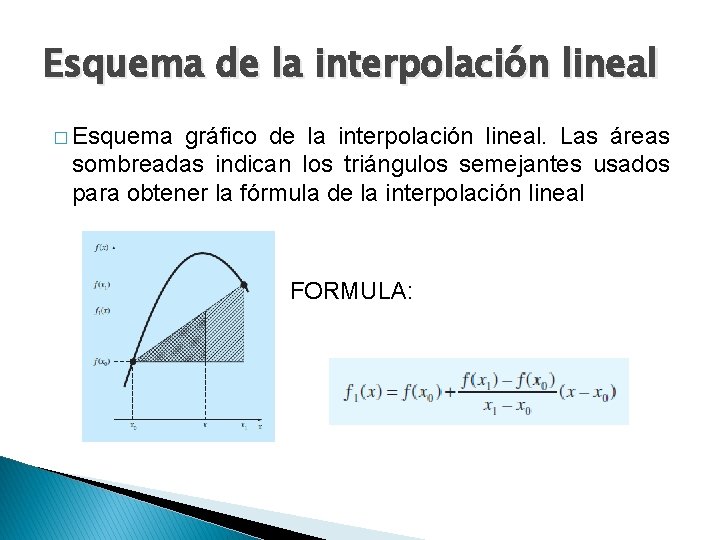
Esquema de la interpolación lineal � Esquema gráfico de la interpolación lineal. Las áreas sombreadas indican los triángulos semejantes usados para obtener la fórmula de la interpolación lineal � FORMULA:

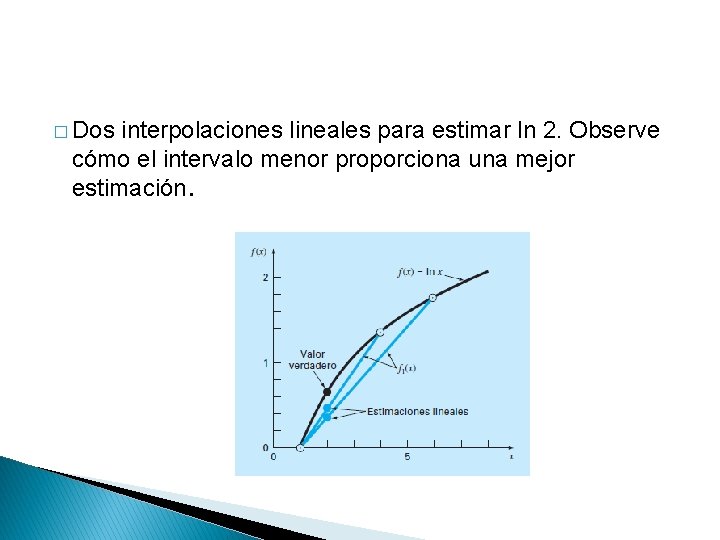
EJERCICIO � Estime el logaritmo natural de 2 mediante interpolación � lineal. Primero, realice el cálculo por interpolación entre ln 1 = 0 y ln 6 = 1. 791759. Después, repita el procedimiento, pero use un intervalo menor de ln 1 a ln 4 (1. 386294). � Observe que el valor verdadero de ln 2 es 0. 6931472.

Solución �

� Dos interpolaciones lineales para estimar ln 2. Observe cómo el intervalo menor proporciona una mejor estimación.

Ejemplo: interpolación cuadrática Ajuste un polinomio de segundo grado a los tres puntos del ejemplo anterior: x 0 = 1 f(x 0) = 0 x 1 = 4 f(x 1) = 1. 386294 x 2 = 6 f(x 2) = 1. 791759

Ejemplo: Polinomios interpolación de Newton diferencias divididas de en

x 0 = 1 f(x 0) = 0 x 1 = 4 f(x 1) = 1. 386294 x 2 = 6 f(x 2) = 1. 791759 x 3 = 5 f(x 3) = 1. 609438 SOLUCION:

FORMULA:

FORMULA:

FORMULA:

FORMULA:

5. 2 Polinomio de interpolación de Lagrange.

5. 2 Polinomio de interpolación de Lagrange. �

5. 2 Polinomio de interpolación de Lagrange. � El polinomio de interpolación de Lagrange es simplemente una reformulación del polinomio de Newton que evita el cálculo de las diferencias divididas, y se representa de manera concisa como: Donde Π designa el “producto de”.

5. 2 Polinomio de interpolación de Lagrange. �

5. 2 Polinomio de interpolación de Lagrange. �

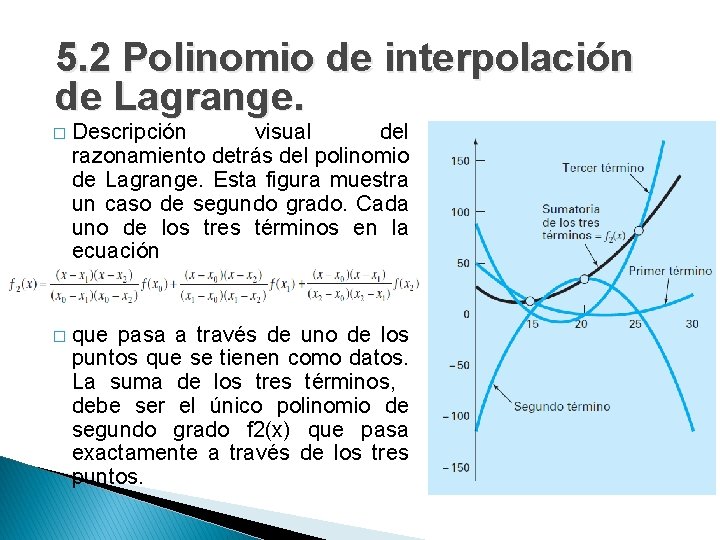
5. 2 Polinomio de interpolación de Lagrange. � Descripción visual del razonamiento detrás del polinomio de Lagrange. Esta figura muestra un caso de segundo grado. Cada uno de los tres términos en la ecuación � que pasa a través de uno de los puntos que se tienen como datos. La suma de los tres términos, debe ser el único polinomio de segundo grado f 2(x) que pasa exactamente a través de los tres puntos.

Ejemplo: �

Ejemplo: � De manera similar, el polinomio de segundo grado se desarrolla así:

5. 3 Interpolación segmentada.

5. 3 Interpolación segmentada. Esta interpolación se llama interpolación segmentaria o interpolación por splines. Una función spline está formada por varios polinomios, cada uno definido en un intervalo y que se unen entre si bajo ciertas condiciones de continuidad. • Interpolación Segmentada Lineal • Interpolación Segmentada Cuadrática • Interpolación Segmentada Cubica

5. 3 Interpolación segmentada lineal Interpolar una función f(x) de la que se nos dan un número N de pares (x, f(x)) por los que tendrá que pasar nuestra función polinómica P(x). Esta serie de funciones nuestras van a ser lineales, de la forma P(x) = ax + b. Definiremos una de estas funciones por cada par de puntos adyacentes, hasta un total de (N-1) funciones, haciéndolas pasar obligatoriamente por los puntos que van a determinarla, la función P(x) será el conjunto de segmentos que unen nodos consecutivos;

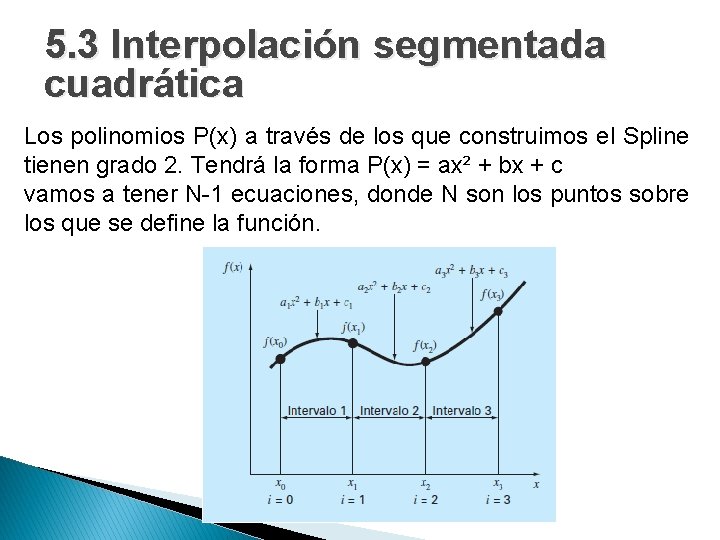
5. 3 Interpolación segmentada cuadrática Los polinomios P(x) a través de los que construimos el Spline tienen grado 2. Tendrá la forma P(x) = ax² + bx + c vamos a tener N-1 ecuaciones, donde N son los puntos sobre los que se define la función.

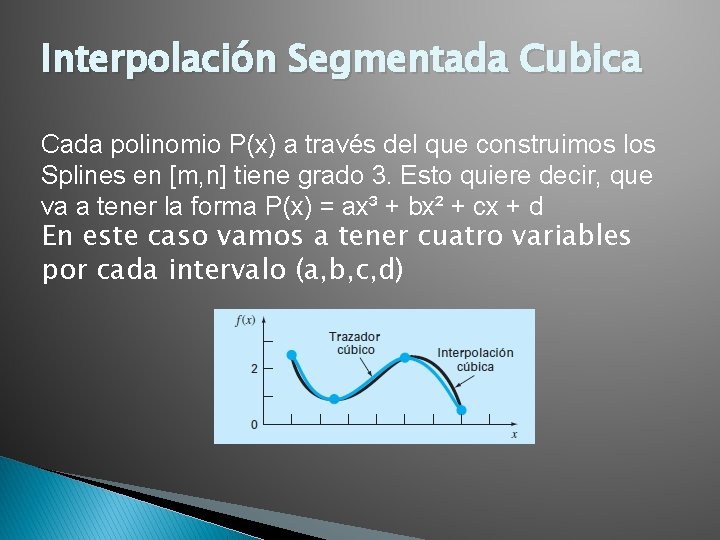
Interpolación Segmentada Cubica Cada polinomio P(x) a través del que construimos los Splines en [m, n] tiene grado 3. Esto quiere decir, que va a tener la forma P(x) = ax³ + bx² + cx + d En este caso vamos a tener cuatro variables por cada intervalo (a, b, c, d)

Ejemplo: Interpolación segmentada. Encontrar la ecuación de segundo grado mediante la interpolación segmentada de la siguiente grafica : y=ax^2+bx+c

5. 4 Problemas de aplicación. � Se puede utilizar en el cálculo de estructuras, instalaciones eléctricas, hidráulicas y sanitarias, en cálculos de carreteras, topografía y hasta en diseño de las estructuras, no en todos los casos pero principalmente cuando hay mala toma de datos o haya datos faltantes.

5. 4 Problemas de aplicación. � � Para el ajuste de curvas, los splines se utilizan para aproximar formas complicadas. La simplicidad de la representación y la facilidad de cómputo de los splines los hacen populares para la representación de curvas en informática, particularmente en el terreno de los gráficos por ordenado. Tenemos los siguientes 3: · Interpolación Segmentaría Lineal · Interpolación Segmentaría Cuadrática · Interpolación Segmentaría Cúbica