Prof Juliana Schivani Schivani Valor numrico P x

Profª Juliana Schivani

Schivani Valor numérico: • P (x) = 10 x 6 – 15 x 5 + 20 x 4 P (2) = 10 ∙ 26 – 15 ∙ 25 + 20 ∙ 24 P (2) = 640 – 480 + 320 = 480

Schivani Raiz de um polinômio: É o valor que a variável x assume para o qual o polinômio se torne nulo, isto é P(x) = 0. P (x) = x 3 + x² - 4 x + 6 P (-3) = (-3)³ + (-3)² - 4 ∙ (-3) + 6 P (-3) = - 27 + 9 + 12 + 6 P (-3) = 0

Schivani A numeração usada na confecção de sapatos depende do comprimento do pé das pessoas. Os fabricantes de calçados brasileiros usam a fórmula N = 5 c + 28, 28 em que c é o tamanho do pé em cm e 4 N é o número do calçado. 1. Existe algum tamanho de pé que zere o polinômio N? 2. Qual o valor numérico deste polinômio para o seu pé?

Schivani A numeração usada na confecção de sapatos depende do comprimento do pé das pessoas. Os fabricantes de calçados brasileiros usam a fórmula N = 5 c + 28 em que c é o tamanho do pé em cm e 4 N é o número inteiro do calçado.

Schivani Decomposição de um polinômio Todo polinômio pode ser decomposto em fatores do primeiro grau da forma: P(x) = an ∙ (x – r 1) ∙ (x – r 2) ∙. . . ∙ (x – rn) Onde r 1, r 2, . . , rn são raízes do polinômio e an é o coeficiente dominante. Todo polinômio de grau n tem exatamente n raízes complexas.

Schivani Decomposição de um polinômio Exemplo: P(x) = x³ - 4 x² - 11 x + 30 = (x – 2) (x + 3) (x – 5) 2, - 3 e 5 são as raízes de P(x), valores estes que cortam Ox no plano cartesiano. P(x) é divisível por cada um dos seus fatores.

Schivani Quando o grau do polinômio é maior ou igual a 5, não existe uma fórmula resolutiva, Galois provou esta impossibilidade e encontrou um método para alguns casos.

Schivani CURIOSIDADE: Quando o grau do polinômio é 3 ou 4, é possível determinar as raízes das equações por meio de fórmulas, as quais, não são estudadas no ensino médio. Estas fórmulas foram descobertas por volta do séc. XVI por matemáticos que participam de duelos os quais cobriamlhes de créditos, prestígios e proteções da nobreza. A foto mostra o Pátio da Igreja de Santa Maria dei Servi na Itália onde eram realizados desafios de matemática.

Schivani Resolver a equação x³ - 8 x² + 29 x – 52 = 0, sabendo que uma das raízes é 4. Como grau p(x) é 3, então existem, além do 4, mais outras duas raízes, (r 2 e r 3). P(x) = 1 ∙ (x – 4) (x – r 2) (x – r 3) P(x) é divisível por cada fator, então, P(x) é divisível por (x – 4) e o quociente desta divisão é exatamente (x – r 2) (x – r 3) P(x) / (x – 4) = x² - 4 x + 13 com raízes = (4 ± √-36) / 2

Schivani Multiplicidade de Raízes Quais são as raízes da equação polinomial x² - 12 x + 36 = 0 ? x’ = x” = 6 6 é raiz dupla / raiz de multiplicidade 2 da equação

Schivani Multiplicidade de Raízes Resolver a equação (x + 4)³ ∙ (x – 1)² ∙ (x + 5) = 0. (x + 4) ∙ (x – 1) ∙ (x + 5) = 0 x + 4 = 0 => x = - 4 (três vezes): -4 é raiz tripla ou x – 1 = 0 => x = 1 (duas vezes): 1 é raiz dupla ou x + 5 = 0 => x = -5 (uma vez): -5 é raiz simples Portanto, P(x), cujo grau é 6, tem 6 raízes.

Schivani Encontrando Raízes Racionais Teorema das raízes racionais: Seja o polinômio anxn + an-1 xn-1 +. . . + a 1 x + ao = 0, com an ≠ 0 e todos os coeficientes inteiros. Se ao e an são primos entre si, isto é, formam uma fração irredutível, as possíveis raízes racionais do polinômio serão todos os divisores de p/q, onde p = ao e q = na.

Schivani Teorema das raízes racionais DEMOSTRAÇÃO Se p/q é raiz da equação, então: Multiplicando ambos os membros por qn: Isolamos anpn e colocamos q em evidência:

Schivani Teorema das raízes racionais DEMOSTRAÇÃO Se p/q é raiz da equação, então: Multiplicando ambos os membros por qn: Isolamos a 0 qn e colocamos p em evidência:

Schivani Teorema das raízes racionais DEMOSTRAÇÃO

Schivani Encontrar as possíveis raízes racionais da equação 3 x 4 + 16 x³ + 29 x² + 26 x + 6 = 0 a 4 = 3 e a n = 6 Se existe alguma raiz racional p/q então p será divisível por 6 e q por 3. p = {-1, -2, -3, -6, 1, 2, 3, 6} e q = {-1, -3, 1, 3} p/q = {± 1, ± 2, ± 3, ± 6, ± 1/3, ± 2/3} Para saber quais são as verdadeiras raízes racionais, deve-se testar cada uma, substituindo-a na equação.

Schivani Encontrar as raízes racionais da equação

Schivani Verificar se o polinômio a seguir possui raiz racional

Schivani Encontrar as raízes racionais da equação Assim, x³ - 7 x + 6 = (x – 1) (x – r 2) (x – r 3)

Schivani Encontrar as raízes racionais da equação x³ - 7 x + 6 = (x – 1) (x – r 2) (x – r 3) 1 1 0 -7 6 1 1 -6 0 quociente Portanto, Q(x) = x² + x – 6 e R(x) = 0 Por Bhaskara, descobrindo as outras duas raízes: 2 e – 3.

Schivani Encontrar as raízes racionais de 3 x³ - 7 x² + 8 x - 2 = 0 a 3 = 3 e an = -2 Se existe alguma raiz real p/q então p será divisível por -2 e q por 3. p = {-1, -2, 1, 2} e q = {-1, -3, 1, 3} p/q = {± 1, ± 1/3, ± 2/3} Apenas P (1/3) = 0, portanto, a única raiz racional deste polinômio é 1/3.

Schivani Encontrar as raízes racionais de 3 x³ - 7 x² + 8 x - 2 = 0 Já sabendo que 1/3 é raiz, então: 3 x³ - 7 x² + 8 x – 2 = 3 (x – 1/3) (x – r 2) (x – r 3) 1/3 3 3 -7 8 -2 -6 6 0 Q(x) = 3 x² - 6 x + 6 x’ = 1 - √-1 e x” = 1 + √-1

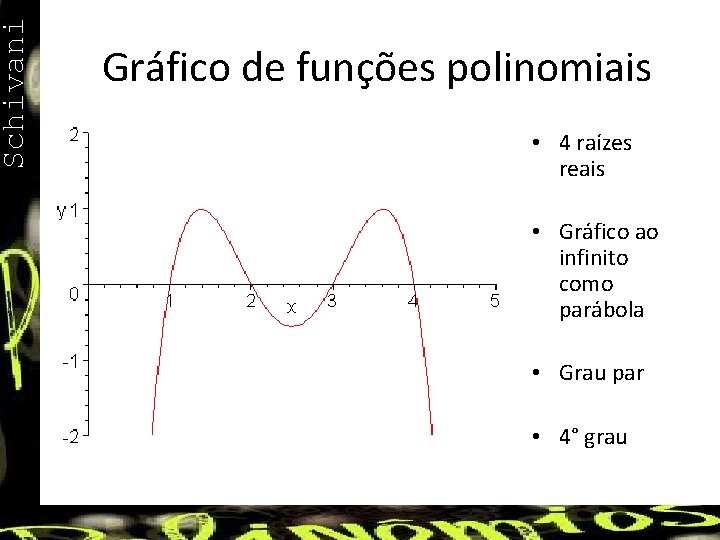
Schivani Gráfico de funções polinomiais • O gráfico toca Ox nos pontos em que tem-se raízes reais. • O gráfico sempre tocará Oy em ao. • Se o polinômio só possuir raízes complexas, então o gráfico não corta Ox. • As raízes complexas sempre aparecem aos pares, portanto, o polinômio de grau ímpar sempre terá pelo menos uma raiz real, e por isso, sempre cortará Ox. • Polinômios de grau par tem gráfico indo para o infinito em forma de parábola. • Polinômios de grau ímpar tem gráfico indo para o infinito em forma de reta.

Schivani Gráfico de funções polinomiais • 4 raízes reais • Gráfico ao infinito como parábola • Grau par • 4° grau

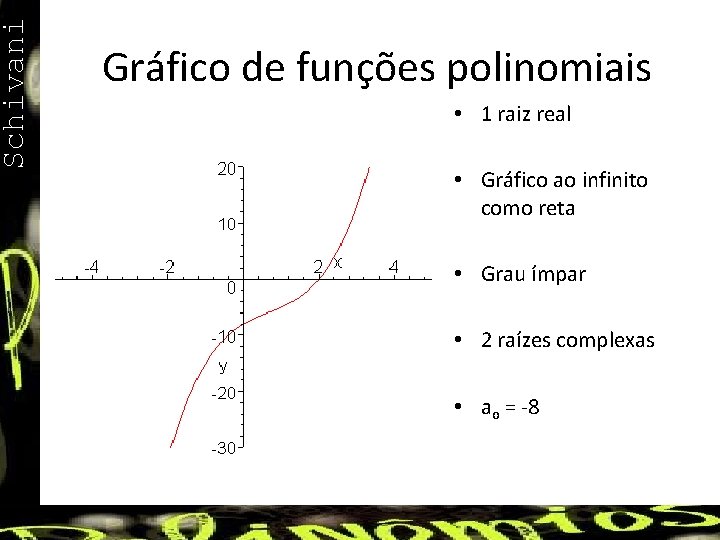
Schivani Gráfico de funções polinomiais • 1 raiz real • Gráfico ao infinito como reta • Grau ímpar • 2 raízes complexas • ao = -8

Schivani

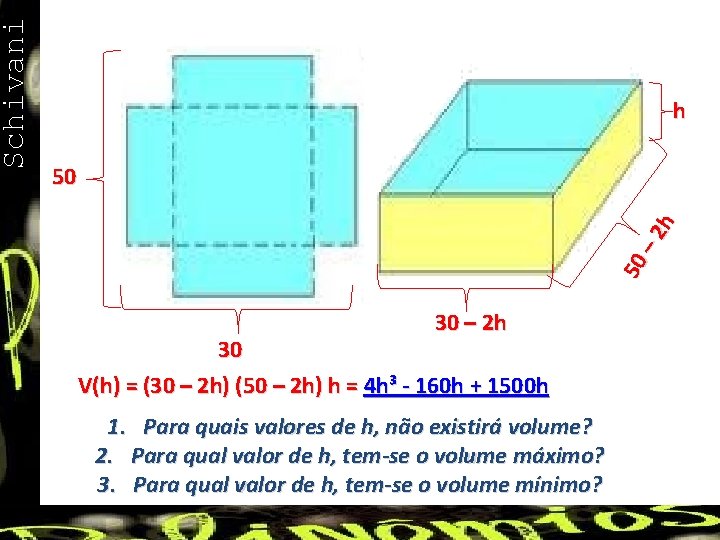
2 h 50 50 – Schivani h 30 – 2 h 30 V(h) = (30 – 2 h) (50 – 2 h) h = 4 h³ - 160 h + 1500 h 1. Para quais valores de h, não existirá volume? 2. Para qual valor de h, tem-se o volume máximo? 3. Para qual valor de h, tem-se o volume mínimo?

Schivani Relações de Girard São relações existentes entre as raízes de um polinômio.

Schivani Demonstração das Relações de Girard

Schivani Demonstração das Relações de Girard

Schivani Demonstração das Relações de Girard

Schivani Referências: • SMOLE, Kátia; DINIZ, Maria Ignez. Matemática 3. 6ª ed. São Paulo: Saraiva, 2010. • IEZZI, Gelson; [et al. ]. Matemática: Ciência e Aplicações. Vol. 3. 6ª ed. São Paulo: Saraiva, 2010. • http: //inf. unioeste. br/~rogerio/02 d-Estudoanalitico-polinomios. pdf

Profª Juliana Schivani juliana. schivani@ifrn. edu. br docente. ifrn. edu. br/juliana