UKURAN PEMUSATAN NILAI SENTRAL DISPERSI SKEWNES DAN KURTOSIS

UKURAN PEMUSATAN (NILAI SENTRAL) DISPERSI, SKEWNES DAN KURTOSIS OLEH : MOH. AMIN, SE. , MSA

Ukuran Pemusatan Data (Central Tendency) - Salah satu aspek yang paling penting untuk menggambarkan distribusi data adalah nilai pusat data pengamatan (tendensi sentral). Setiap pengukuran aritmatika yang ditujukan untuk menggambarkan suatu nilai yang mewakili nilai pusat atau nilai sentral dari suatu gugus data (himpunan pengamatan) dikenal sebagai ukuran tendensi sentral. - Merupakan nilai tunggal yang mewakili semua data atau kumpulan pengamatan dimana nilai tersebut menunjukkan pusat data.

Yang termasuk ukuran pemusatan dan letak data : 1. Rata-rata hitung 2. Median 3. Modus 4. Rata-rata ukur 5. Rata-rata harmonis 6. Kwartil, desil dan persentil.

1. RATA-RATA HITUNG adalah : sering disebut dengan istilah mean saja. merupakan metode yang paling banyak digunakan untuk menggambarkan ukuran tendensi sentral. Mean dihitung dengan menjumlahkan semua nilai data pengamatan kemudian dibagi dengan banyaknya data. Yang biasa disebut rata-rata dalam kehidupan sehari-hari adalah rata-rata hitung.

PERNAHKAH MENDENGAR PERNYATAAN INI? v Berapa rata-rata nilai ulangan statistika di kelasmu? v Tinggi badan rata-rata mahasiswa kelas J adalah 156 cm v Berapa keuntungan rata-rata yang diperoleh petani padi setiap musim dalam satu tahun? v Berapa rata-rata jumlah kendaraan bermotor yang melintasi Jalan Jenderal Sudirman setiap menit?

1. RATA-RATA HITUNG Rata-rata hitung populasi dinyatakan dengan lambang dibaca “mu”, sedangkan rata-rata hitung sampel dinyatakan dengan lambang dibaca “x bar” atau dan lain-lain, tergantung lambang yang digunakan untuk menyatakan variable yang sedang dicari rata-ratanya.

1. RATA-RATA HITUNG terdapat dua cara untuk menghitung nilai rata-rata hitung 1. rata-rata hitung untuk data yang belum dikelompokkan (ungrouped data) 2. Rata-rata hitung yang telah dikelompokan (grouped data) Terbagi dalam dua metode : - Rata-rata hitung dengan metode panjang (long Method) - Rata-rata hitung dengan metode pendek (short Method)

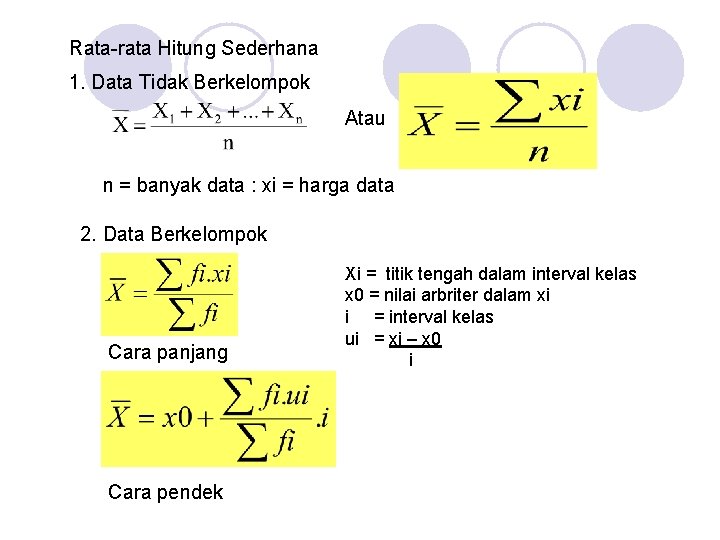
Rata-rata Hitung Sederhana 1. Data Tidak Berkelompok Atau n = banyak data : xi = harga data 2. Data Berkelompok Cara panjang Cara pendek Xi = titik tengah dalam interval kelas x 0 = nilai arbriter dalam xi i = interval kelas ui = xi – x 0 i

Contoh soal 1 Nilai ulangan statistika 5 mahasiswa akuntansi kelas J adalah 8, 5, 7, 10, dan 5. tentukan nilai rata-rata dari nilai 5 mahasiswa akuntansi kelas J tersebut. . . ?

Pembahasan soal 1 Dik : Data = 8, 5, 7, 10, 5 n = banyak data = jumlah data Ditanya : rata-rata Jawab : = = 7 =5 = 8 + 5 + 7 + 10 + 5 = 35

Contoh soal 2 Berat badan 10 orang mhs kls J adalah z, 48, 50, 44, 46, 50, 56, 57, 44, dan 45 kg. Jika berat badan rata-rata ke 10 mahasiswa tersebut 50 kg, nilai yang benar untuk z adalah …. Kg.

Pembahasan soal 2 Diketahui : banyak data = n Rata-rata Jumlah data Ditanya : z = 10 = 50 = z + 48+50+44+46+50 +56+57+44+45 = z + 440 Jawab : 50 = z + 440 = 50. 10 z + 440 = 500 z = 500 – 440 z = 60

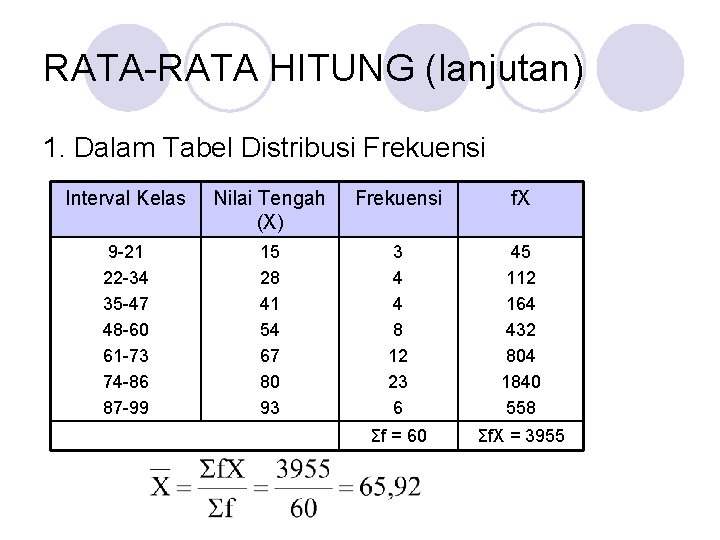
RATA-RATA HITUNG (lanjutan) 1. Dalam Tabel Distribusi Frekuensi Interval Kelas Nilai Tengah (X) Frekuensi f. X 9 -21 22 -34 35 -47 48 -60 61 -73 74 -86 87 -99 15 28 41 54 67 80 93 3 4 4 8 12 23 6 45 112 164 432 804 1840 558 Σf = 60 Σf. X = 3955

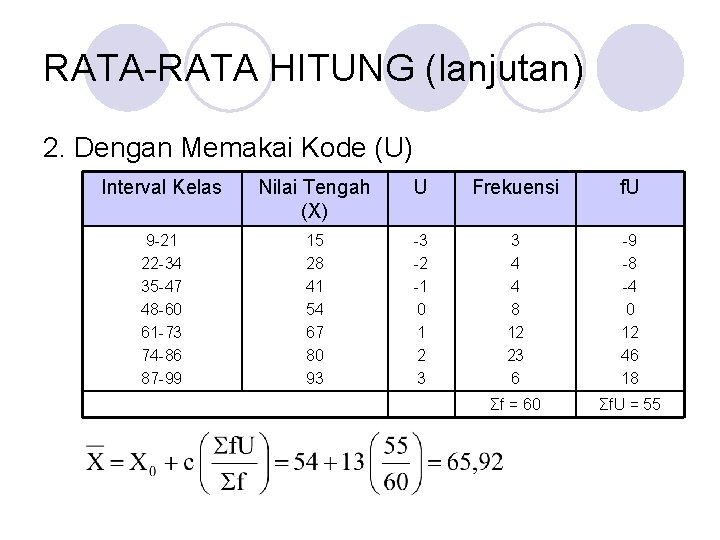
RATA-RATA HITUNG (lanjutan) 2. Dengan Memakai Kode (U) Interval Kelas Nilai Tengah (X) U Frekuensi f. U 9 -21 22 -34 35 -47 48 -60 61 -73 74 -86 87 -99 15 28 41 54 67 80 93 -3 -2 -1 0 1 2 3 3 4 4 8 12 23 6 -9 -8 -4 0 12 46 18 Σf = 60 Σf. U = 55

RATA-RATA HITUNG (lanjutan) 3. Dengan pembobotan Masing-masing data diberi bobot. Misal A memperoleh nilai 65 untuk tugas, 76 untuk mid dan 70 untuk ujian akhir. Bila nilai tugas diberi bobot 2, Mid 3 dan Ujian Akhir 4, maka rata-rata hitungnya adalah :

2. MEDIAN Untuk data berkelompok

MEDIAN (lanjutan) Contoh : Interval Kelas Frekuensi 9 -21 22 -34 35 -47 48 -60 61 -73 74 -86 87 -99 3 4 4 8 12 23 6 Σf = 60 Letak median ada pada data ke 30, yaitu pada interval 61 -73, sehingga : L 0 = 60, 5 F = 19 f = 12

3. MODUS Untuk data berkelompok

MODUS (lanjutan) Contoh : Interval Kelas Frekuensi 9 -21 22 -34 35 -47 48 -60 61 -73 74 -86 87 -99 3 4 4 8 12 23 6 Σf = 60 Data yang paling sering muncul adalah pada interval 74 -86, sehingga : L 0 = 73, 5 b 1 = 23 -12 = 11 b 2 = 23 -6 =17

HUBUNGAN EMPIRIS ANTARA NILAI RATA-RATA HITUNG, MEDIAN, DAN MODUS Ada 3 kemungkinan kesimetrian kurva distribusi data : 1) Jika nilai ketiganya hampir sama maka kurva mendekati simetri. 2) Jika Mod<Med<rata-rata hitung, maka kurva miring ke kanan. 3) Jika rata-rata hitung<Med<Mod, maka kurva miring ke kiri.

HUBUNGAN EMPIRIS ANTARA NILAI RATA-RATA HITUNG, MEDIAN, DAN MODUS (lanjutan) Jika distribusi data tidak simetri, maka terdapat hubungan : Rata-rata hitung-Modus = 3 (Rata-rata hitung-Median)

Tugas rumah nilai F 1– 3 5 4– 6 7 7– 9 9 10 – 12 4 11 – 15 3 16 – 18 2 jumlah 30 1. 2. 3. Tentukan nilai rata – ratanya metode panjang dan pendek Tentukan nilai standar deviasi metode pendek dan panjang Tentukan nilai Skewness (SK/TK)