The Study of Motion l l Galileos axiom

The Study of Motion l l Galileo's axiom: ignorato motu, ignoratur natura " not to know motion is not to know nature “. So We shall begin with the key topic in mechanics, the laws governing some of the simpler motions of objects : » Mathematics and the Description of Motion » Galileo and the Kinematics of Free Fall » Projectile Motion Physics 111: Lecture 2, Pg 1

Constant velocity l l l According to Galileo and Descartes, the natural state of a physical object is rest or motion along a straight line, at constant speed. How the physicist describes such motion in a way that can easily be generalized to other kinds of motion. Galileo (1564 -1642) Suppose we are watching the motion of a car traveling along a perfectly straight and smooth road, and that we wish to find the exact relationship between the distance covered and the time required to cover it, such as table 6. Descartes (1596 -1650) Physics 111: Lecture 2, Pg 2

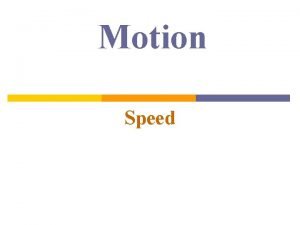
the motion can be written s ~ t, where the symbol ~ means "is proportional to. “ But this is equivalent to the equation s = kt, where k is a constant that depends on neither s nor t. ………. What look like is the graph ? In analytic geometry, the equation s = kt represents a straight line passing through the origin of coordinates. The constant k is called the slope k = s/t This ratio of distance covered to time elapsed is, by definition, the speed; the fact that it is equal to a constant of the car travels with constant or uniform speed. Physics 111: Lecture 2, Pg 3

Motion in 1 dimension l In 1 -D, we usually write position as s(t 1) or x(t 1 ). l Since it’s in 1 -D, all we need to indicate direction is + or . è Displacement in a time t = t 2 - t 1 is x = x(t 2) - x(t 1) = x 2 - x 1 x x some particle’s trajectory in 1 -D x 2 x 1 t 1 t t 2 t Physics 111: Lecture 2, Pg 4

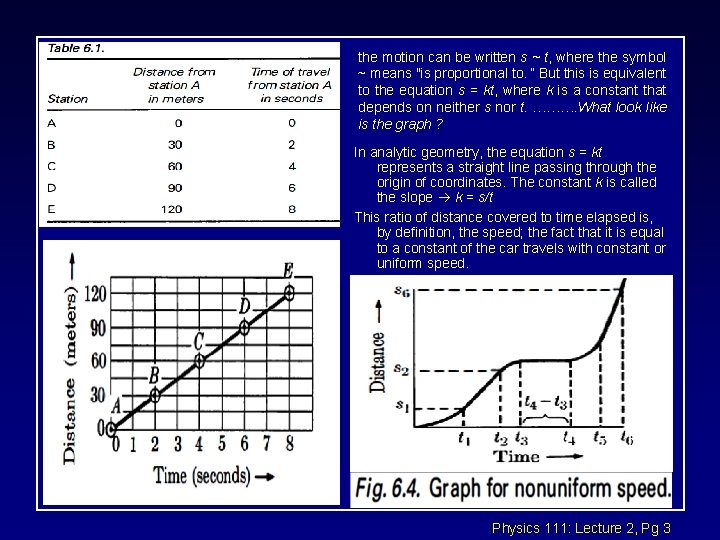
1 -D kinematics l l Velocity v is the “rate of change of position” Average velocity vav in the time t = t 2 - t 1 is: x x trajectory x 2 Vav = slope of line connecting x 1 and x 2. x 1 t 2 t t Physics 111: Lecture 2, Pg 5

1 -D kinematics. . . l l Consider limit t 1 t 2 Instantaneous velocity v is defined as: x x so v(t 2) = slope of line tangent to path at t 2. x 2 x 1 t 2 t t Physics 111: Lecture 2, Pg 6

1 -D kinematics. . . l l Acceleration a is the “rate of change of velocity” Average acceleration aav in the time t = t 2 - t 1 is: l And instantaneous acceleration a is defined as: using Physics 111: Lecture 2, Pg 7

Recap l If the position x is known as a function of time, then we can find both velocity v and acceleration a as a function of time! x v a t t t Physics 111: Lecture 2, Pg 8

More 1 -D kinematics l l We saw that v = dx / dt In “calculus” language we would write dx = v dt, which we can integrate to obtain: l Graphically, this is adding up lots of small rectangles: v(t) + +. . . + = displacement t Physics 111: Lecture 2, Pg 9

1 -D Motion with constant acceleration l High-school calculus: l Also recall that l Since a is constant, we can integrate this using the above rule to find: l Similarly, since we can integrate again to get: Physics 111: Lecture 2, Pg 10

Useful Formula l Solving for t: l Plugging in for t: Physics 111: Lecture 2, Pg 11

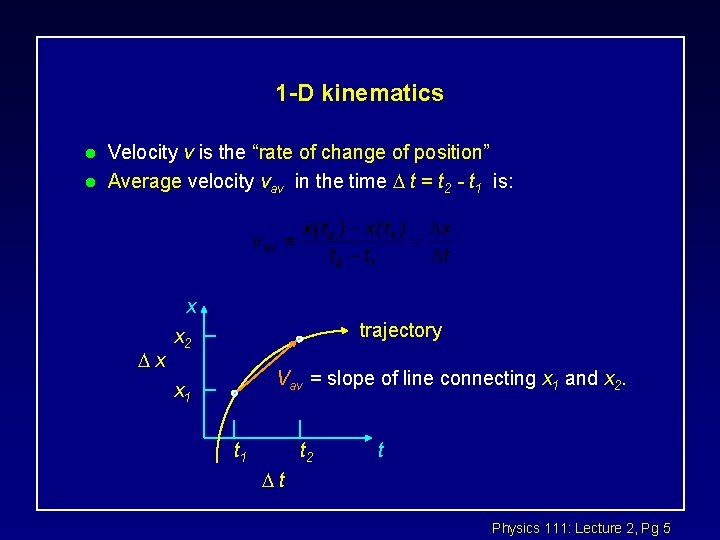
Recap: l For constant acceleration: x v l t From which we know: a t Physics 111: Lecture 2, Pg 12

Lecture 1, Act 2 Motion in One Dimension l When throwing a ball straight up, which of the following is true about its velocity v and its acceleration a at the highest point in its path? (a) Both v = 0 and a = 0. (b) v 0, but a = 0. y (c) v = 0, but a 0. Physics 111: Lecture 2, Pg 13

Lecture 1, Act 2 Solution l Going up the ball has positive velocity, while coming down it has negative velocity. At the top the velocity is momentarily zero. x l Since the velocity is continually changing there must v be some acceleration. çIn fact the acceleration is caused by gravity (g = 9. 81 m/s 2). ç(more on gravity in a few lectures) a l The answer is (c) v = 0, but a 0. t t t Physics 111: Lecture 2, Pg 14

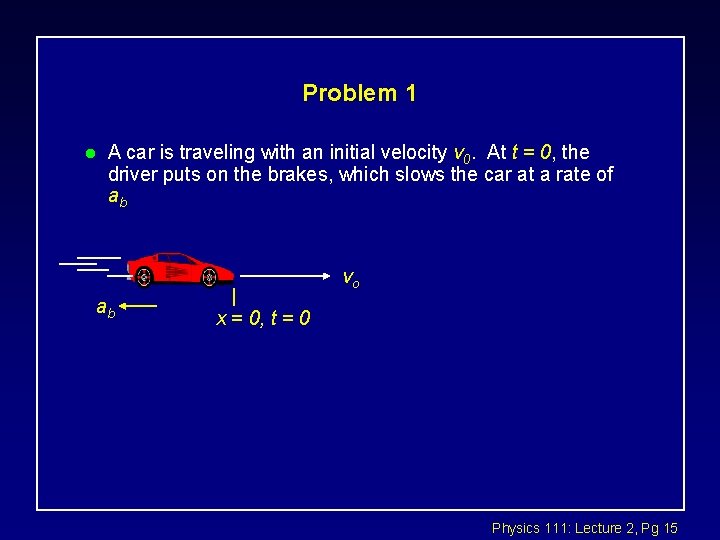
Problem 1 l A car is traveling with an initial velocity v 0. At t = 0, the driver puts on the brakes, which slows the car at a rate of ab vo ab x = 0, t = 0 Physics 111: Lecture 2, Pg 15

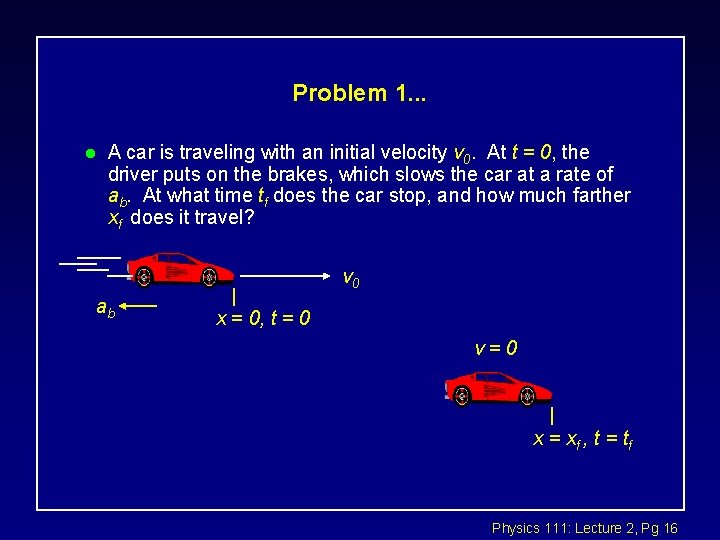
Problem 1. . . l A car is traveling with an initial velocity v 0. At t = 0, the driver puts on the brakes, which slows the car at a rate of ab. At what time tf does the car stop, and how much farther xf does it travel? v 0 ab x = 0, t = 0 v=0 x = xf , t = tf Physics 111: Lecture 2, Pg 16

Problem 1. . . l Above, we derived: v = v 0 + at l Realize that a = -ab l Also realizing that v = 0 at t = tf : find 0 = v 0 - ab tf or tf = v 0 /ab Physics 111: Lecture 2, Pg 17

Problem 1. . . l To find stopping distance we use: l In this case v = vf = 0, x 0 = 0 and x = xf Physics 111: Lecture 2, Pg 18

Problem 1. . . l l l So we found that Suppose that vo = 65 mi/hr = 29 m/s =104. 6 km/hr Suppose also that ab = g = 9. 81 m/s 2 ç Find that tf = 3 s and xf = 43 m Physics 111: Lecture 2, Pg 19

Tips: l Read ! çBefore you start work on a problem, read the problem statement thoroughly. Make sure you understand what information is given, what is asked for, and the meaning of all the terms used in stating the problem. l Watch your units ! çAlways check the units of your answer, and carry the units along with your numbers during the calculation. l Understand the limits ! çMany equations we use are special cases of more general laws. Understanding how they are derived will help you recognize their limitations (for example, constant acceleration). Physics 111: Lecture 2, Pg 20

Review: l For constant acceleration we found: x v l t From which we derived: a t t Physics 111: Lecture 2, Pg 21

Recall what you saw: 12 22 32 42 Physics 111: Lecture 2, Pg 22

1 -D Free-Fall l l This is a nice example of constant acceleration (gravity): In this case, acceleration is caused by the force of gravity: çUsually pick y-axis “upward” y çAcceleration of gravity is “down”: t v t a y ay = g t Physics 111: Lecture 2, Pg 23

Gravity facts: Penny & feather l g does not depend on the nature of the material! çGalileo (1564 -1642) figured this out without fancy clocks & rulers! l demo - feather & penny in vacuum l Nominally, g = 9. 81 m/s 2 çAt the equator g = 9. 78 m/s 2 çAt the North pole g = 9. 83 m/s 2 l More on gravity in a few lectures! Physics 111: Lecture 2, Pg 24

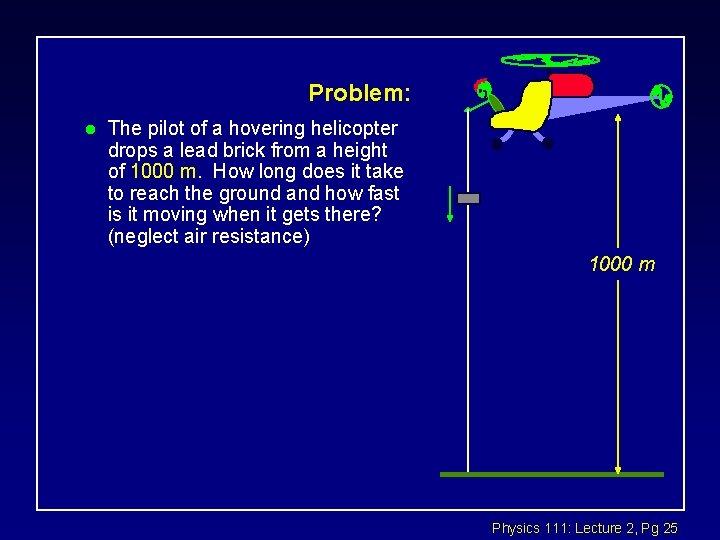
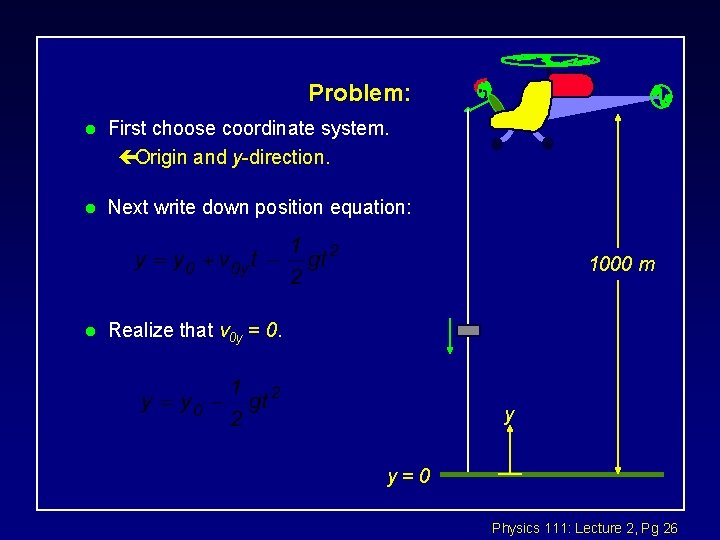
Problem: l The pilot of a hovering helicopter drops a lead brick from a height of 1000 m. How long does it take to reach the ground and how fast is it moving when it gets there? (neglect air resistance) 1000 m Physics 111: Lecture 2, Pg 25

Problem: l First choose coordinate system. çOrigin and y-direction. l Next write down position equation: 1000 m l Realize that v 0 y = 0. y y=0 Physics 111: Lecture 2, Pg 26

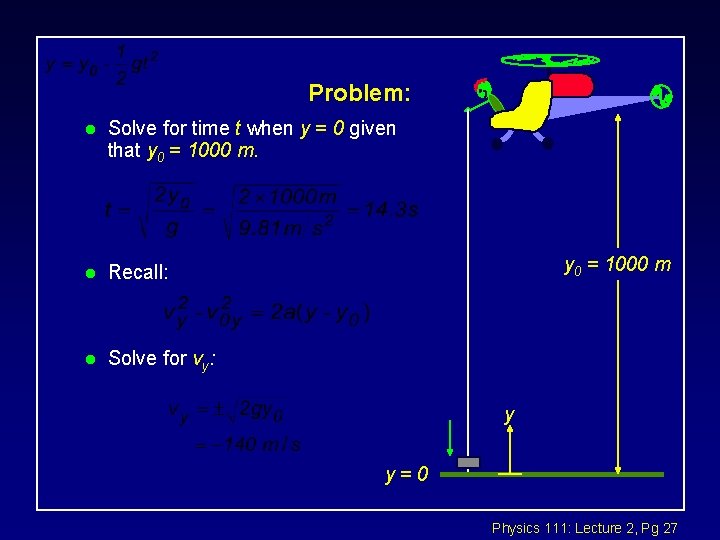
Problem: l Solve for time t when y = 0 given that y 0 = 1000 m. l Recall: l Solve for vy: y 0 = 1000 m y y=0 Physics 111: Lecture 2, Pg 27

Lecture 2, Act 1 1 D free fall l Alice and Bill are standing at the top of a cliff of height H. Both throw a ball with initial speed v 0, Alice straight down and Bill straight up. The speed of the balls when they hit the ground are v. A and v. B respectively. Which of the following is true: (a) v. A < v. B (b) v. A = v. B Alice v 0 (c) v. A > v. B Bill H v. A v. B Physics 111: Lecture 2, Pg 28

Lecture 2, Act 1 1 D Free fall l Since the motion up and back down is symmetric, intuition should tell you that v = v 0 çWe can prove that your intuition is correct: Equation: This looks just like Bill threw the ball down with speed v 0, so the speed at the bottom should be the same as Alice’s ball. Bill v 0 v = v 0 H y=0 Physics 111: Lecture 2, Pg 29

Lecture 2, Act 1 1 D Free fall l We can also just use the equation directly: Alice: same !! Bill: Alice v 0 Bill y=0 Physics 111: Lecture 2, Pg 30

2 -D Kinematics l Most 3 -D problems can be reduced to 2 -D problems when acceleration is constant: çChoose y axis to be along direction of acceleration çChoose x axis to be along the “other” direction of motion l Example: Example Throwing a baseball (neglecting air resistance) çAcceleration is constant (gravity) çChoose y axis up: ay = -g çChoose x axis along the ground in the direction of the throw Physics 111: Lecture 2, Pg 31

Vectors (review): l In 1 dimension, we could specify direction with a + or - sign. For example, in the previous problem ay = -g etc. l In 2 or 3 dimensions, we need more than a sign to specify the direction of something: l To illustrate this, consider the position vector r in 2 dimensions. Example: Example Where is G. Merapi? çChoose origin at Jogjakarta çChoose coordinates of distance (kilometers), and direction (N, S, E, W) çIn this case r is a vector that points 35 km north. G. Merapi r Jogjakarta Physics 111: Lecture 2, Pg 32

Unit Vectors: l l l A Unit Vector is a vector having length 1 and no units It is used to specify a direction Unit vector u points in the direction of U çOften denoted with a “hat”: u = û U û y l Useful examples are the Cartesian unit vectors [ i, j, k ] ç point in the direction of the x, y and z axes j z k i x Physics 111: Lecture 2, Pg 33

Vectors. . . l The components of r are its (x, y, z) coordinates ç r = (rx , ry , rz ) = (x, y, z) l Consider this in 2 -D (since it’s easier to draw): çrx = r cos where r = |r | ; çry = r sin arctan( y / x ) (x, y) y r l x The length of a vector clearly does not depend on its direction. Physics 111: Lecture 2, Pg 34

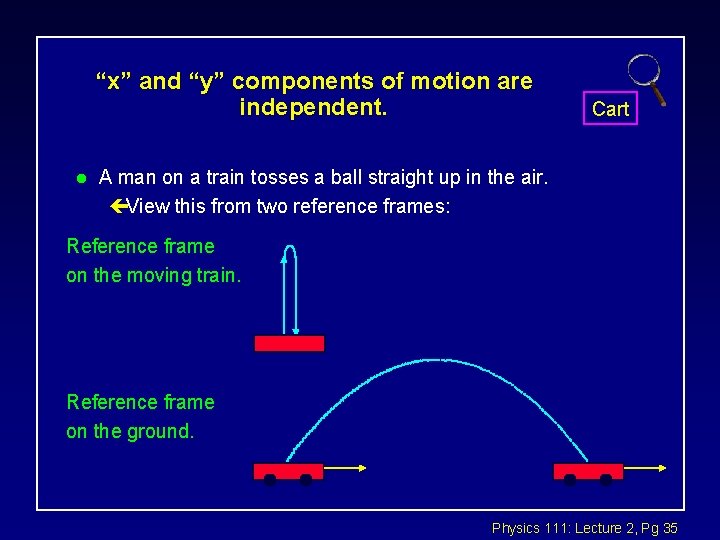
“x” and “y” components of motion are independent. l Cart A man on a train tosses a ball straight up in the air. çView this from two reference frames: Reference frame on the moving train. Reference frame on the ground. Physics 111: Lecture 2, Pg 35

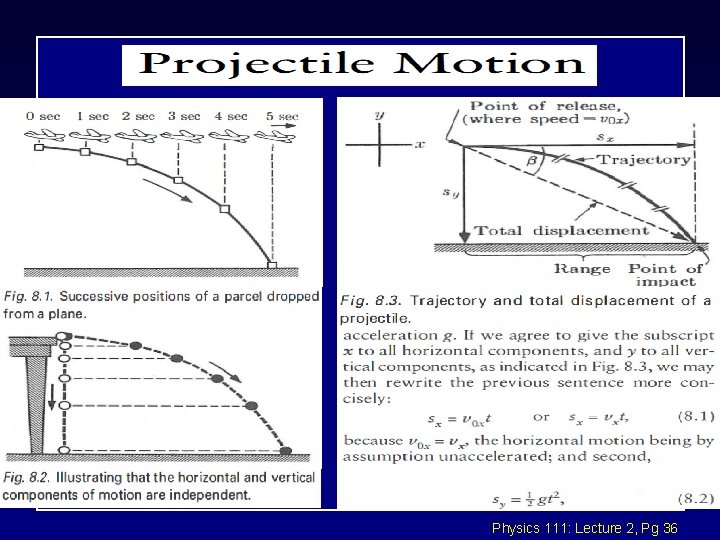
Physics 111: Lecture 2, Pg 36

From eq. (8. 1) and (8. 2) Physics 111: Lecture 2, Pg 37

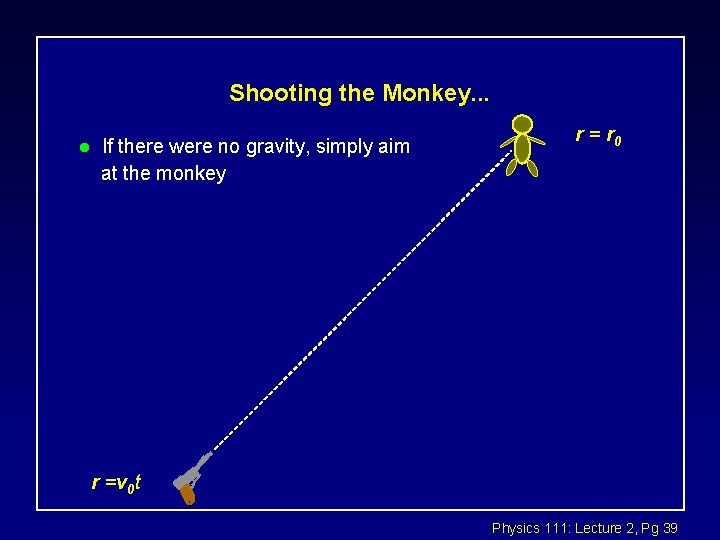
Shooting the Monkey (tranquilizer gun) l Where does the zookeeper aim if he wants to hit the monkey? ( He knows the monkey will let go as soon as he shoots ! ) Physics 111: Lecture 2, Pg 38

Shooting the Monkey. . . l If there were no gravity, simply aim at the monkey r = r 0 r =v 0 t Physics 111: Lecture 2, Pg 39

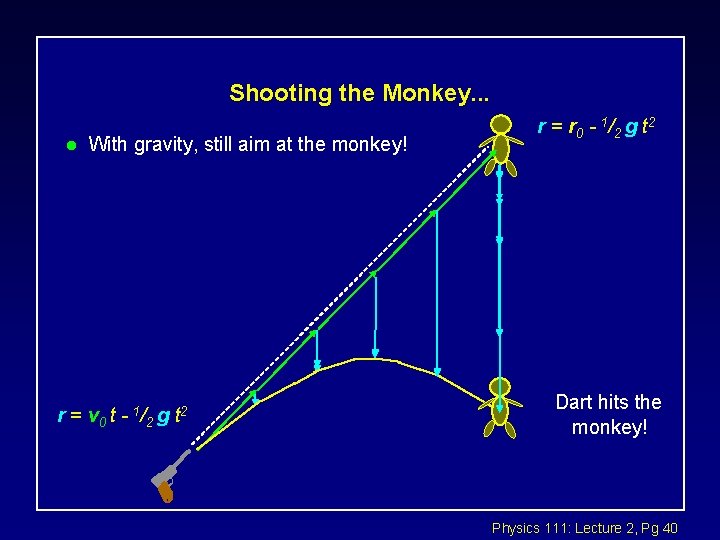
Shooting the Monkey. . . l With gravity, still aim at the monkey! r = v 0 t - 1 / 2 g t 2 r = r 0 - 1 / 2 g t 2 Dart hits the monkey! Physics 111: Lecture 2, Pg 40

Recap: Shooting the monkey. . . x = v 0 t y = - 1 /2 g t 2 l This may be easier to think about. It’s exactly the same idea!! x = x 0 y = - 1 /2 g t 2 Physics 111: Lecture 2, Pg 41

Physics 111: Lecture 2, Pg 42

To summarize Physics 111: Lecture 2, Pg 43

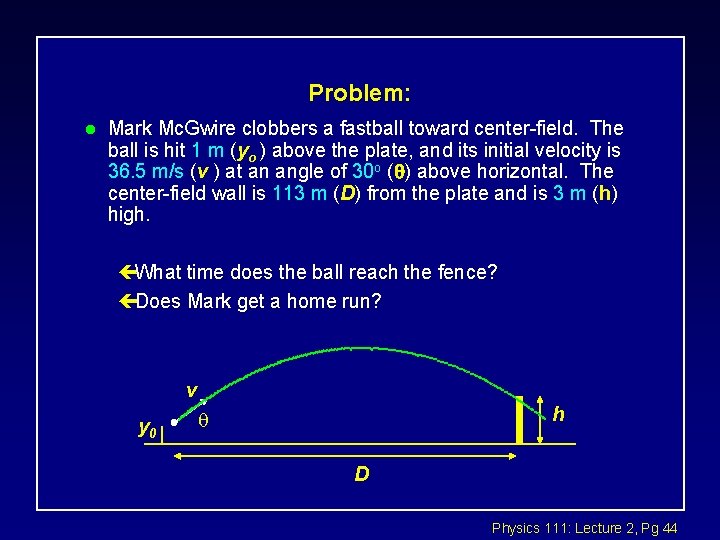
Problem: l Mark Mc. Gwire clobbers a fastball toward center-field. The ball is hit 1 m (yo ) above the plate, and its initial velocity is 36. 5 m/s (v ) at an angle of 30 o ( ) above horizontal. The center-field wall is 113 m (D) from the plate and is 3 m (h) high. çWhat time does the ball reach the fence? çDoes Mark get a home run? v y 0 h D Physics 111: Lecture 2, Pg 44

Problem. . . l l l Choose y axis up. Choose x axis along the ground in the direction of the hit. Choose the origin (0, 0) to be at the plate. Say that the ball is hit at t = 0, x = x 0 = 0 Distance s x çEquations of motion are: vx = v 0 x x = vxt vy = v 0 y - gt y = y 0 + v 0 y t - 1/ 2 gt 2 Physics 111: Lecture 2, Pg 45

Problem. . . l Use geometry to figure out v 0 x and v 0 y : y g v y 0 Find and v 0 x = |v| cos . v 0 y = |v| sin . v 0 y v 0 x x Physics 111: Lecture 2, Pg 46

Problem. . . l l The time to reach the wall is: t = D / vx (easy!) We have an equation that tell us y(t) = y 0 + v 0 y t + a t 2/ 2 So, we’re done. . now we just plug in the numbers: Find: ç vx = 36. 5 cos(30) m/s = 31. 6 m/s ç vy = 36. 5 sin(30) m/s = 18. 25 m/s ç t = (113 m) / (31. 6 m/s) = 3. 58 s ç y(t) = (1. 0 m) + (18. 25 m/s)(3. 58 s) (0. 5)(9. 8 m/s 2)(3. 58 s)2 = (1. 0 + 65. 3 - 62. 8) m = 3. 5 m ç Since the wall is 3 m high, Mark gets the homer!! Physics 111: Lecture 2, Pg 47

Lecture 2, Act 3 Motion in 2 D l Two footballs are thrown from the same point on a flat field. Both are thrown at an angle of 30 o above the horizontal. Ball 2 has twice the initial speed of ball 1. If ball 1 is caught a distance D 1 from the thrower, how far away from the thrower D 2 will the receiver of ball 2 be when he catches it? (a) D 2 = 2 D 1 (b) D 2 = 4 D 1 (c) D 2 = 8 D 1 Physics 111: Lecture 2, Pg 48

Lecture 2, Act 3 Solution l l l The distance a ball will go is simply x = (horizontal speed) x (time in air) = v 0 x t To figure out “time in air”, consider the equation for the height of the ball: When the ball is caught, y = y 0 (time of catch) two solutions (time of throw) Physics 111: Lecture 2, Pg 49

Lecture 2, Act 3 Solution x = v 0 x t l So the time spent in the air is proportional to v 0 y : l Since the angles are the same, both v 0 y and v 0 x for ball 2 are twice those of ball 1. v 0, 2 ball 1 v 0 x , 1 l v 0, 1 v 0 y , 2 ball 2 v 0 y , 1 v 0 x , 2 Ball 2 is in the air twice as long as ball 1, but it also has twice the horizontal speed, so it will go 4 times as far!! Physics 111: Lecture 2, Pg 50