The firm as a semilattice of activity prolegomenon

The firm as a semilattice of activity: prolegomenon to a theory of the firm Keiran Sharpe UNSW, Canberra

Introduction • Presents a new theory of agency – ‘narrative theory’ – which draws on Philosophy and Sociology • Narrative theory is a theory of planning rather than of decision making • Narrative theory is used to propose a new theory of the firm which can be used to unify various models used in Management theory • Very preliminary stage of development

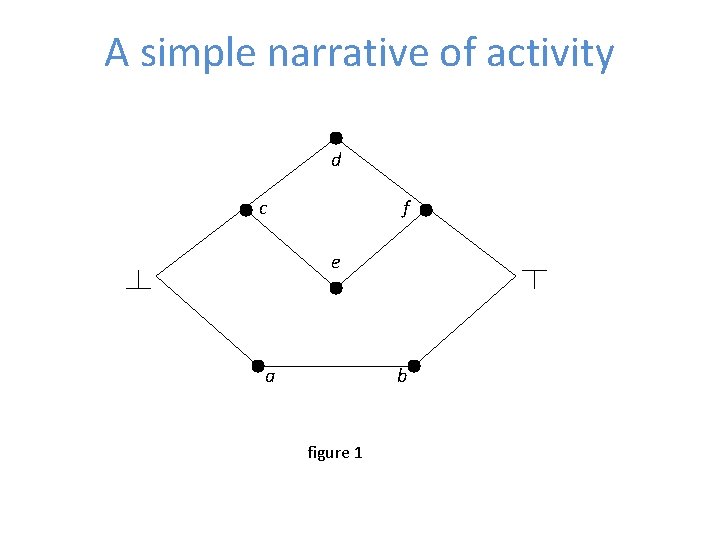
What is a narrative? • A narrative is a partial order of activity that is undertaken for some purpose • Each narrative has a beginning and an end – i. e. the partial order of actions has a top (� ) and bottom (� )

A simple narrative of activity d c f e a b figure 1

Events and Episodes • It’s natural in narrative theory to ask how we might concatenate collections of events – which can be thought of as individual ‘pages’ in the narrative – to form episodes – which may be thought of as ‘chapters’ • The reason we’re interested in doing this is that we think that agents plan by intending to implement chapters – or coarse plans of action – first, which they then refine later into individual pages – or actions

Episodes as partition blocks • Formally, this becomes a query about what conditions must be imposed on blocks and relations between blocks of partitions of the poset. • The conditions imposed should preserve the order and succession relations

Conditions for coarsening a poset • Convexity of blocks • e-Connectedness • e-Closure

Convexity • A set is convex if, whenever we have: b, d B, c A and b �c �d, we have c B. where B is a block of a partition of the poset, A.

e-Connectedness • A set is an upper core of a convex set B (A), and is denoted U(B), when it satisfies: • U(B) b �for all b B • U(B) B = � • B is connected on B U(B), and • U(B) C (A). • Similarly for lower core • e-Connectedness holds if B is connected on the union of B and its upper core and on the union of B and its lower core

e-Closure • a partition, π, is said to be upper e-Closed if each up-path of each element, b, of each set, B, intersects one and only one set, C, containing an upper core, U(B), of that set; i. e. , • for all b B , each up-path of b intersects just one set, C , where U(B) C.

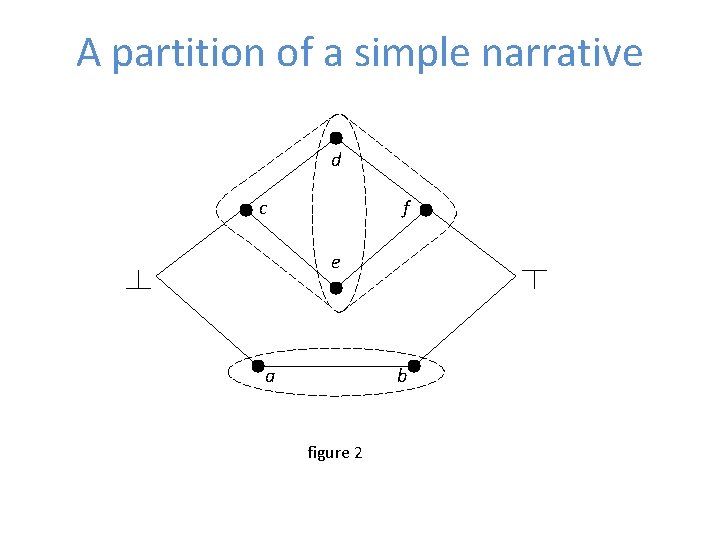
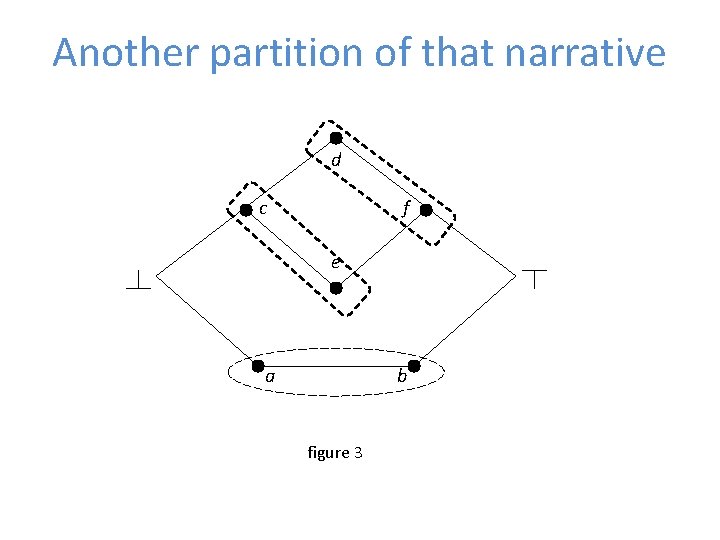
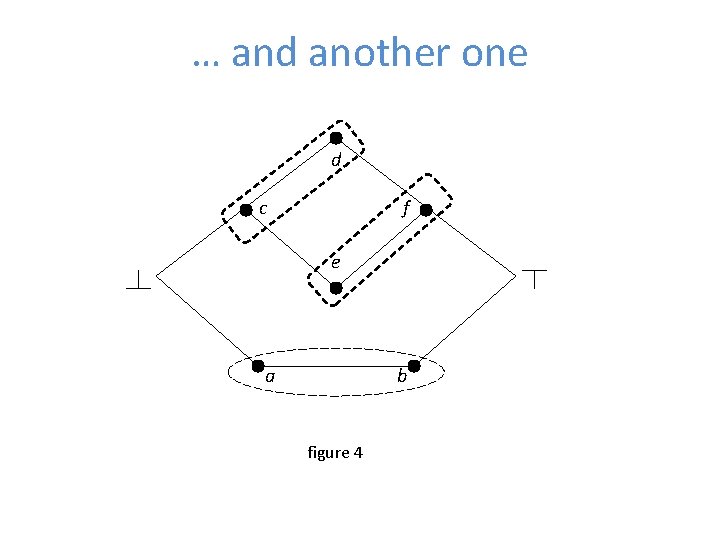
Coarser and finer descriptions • It can then be shown that, if the above three conditions are imposed, then the partition of a partially ordered set is monotonic (orderpreserving) and, in fact, also preserves the succession relation • The following diagrams give examples of various partitions that satisfy the above conditions

A partition of a simple narrative d c f e a b figure 2

Another partition of that narrative d c f e a b figure 3

… and another one d c f e a b figure 4

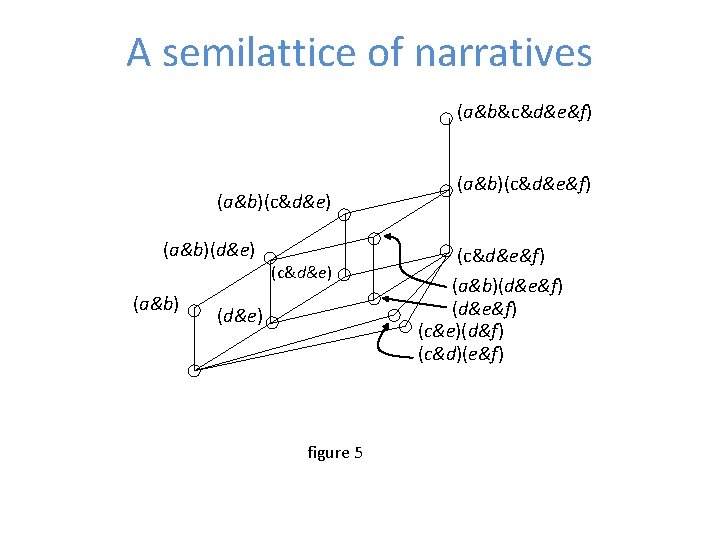
The set of coarsened partitions • The set of coarsened partitions also has a structure • The set of partitions is a poset • The set of partitions is a join semilattice • The following diagram gives the semilattice for the set of partitions of the narrative given in the first diagram

A semilattice of narratives (a&b&c&d&e&f) (a&b)(c&d&e) (a&b)(d&e) (a&b) (c&d&e) (d&e) figure 5 (a&b)(c&d&e&f) (a&b)(d&e&f) (c&e)(d&f) (c&d)(e&f)

Choices between narratives • Our interest in narratives derives from the fact that we think that agents choose between alternative narratives when planning what to do • Two plans are said to be alternative ways of implementing a given, coarser plan, if they both refine the coarser plan but have no common refinement

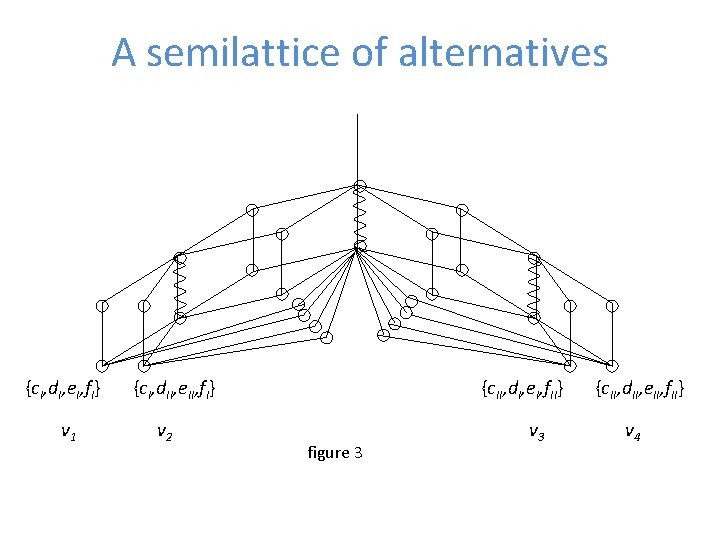
The structure of choices • The set of alternative partitions of different narratives that implement a single, ultimately coarse – or abstract – plan forms a join semilattice • An example of a semilattice of plans related to the narrative given in figure 1 is given in the following diagram

A simple example • In this example, we suppose that the are two possible ways of jointly implementing activities d & e, and two possible way of implementing activities c & f • Hence, there are four possible narratives: {(c. I, f. I), (d. I, e. I)} {(c. I, f. I), (d. II, e. II)} {(c. II, f. II), (d. I, e. I)} {(c. II, f. II), (d. II, e. II)}

A semilattice of alternatives {c. I, d. I, e. I, f. I} v 1 {c. I, d. II, e. II, f. I} v 2 {c. II, d. I, e. I, f. II} figure 3 v 3 {c. II, d. II, e. II, f. II} v 4

Implementing plans • The decision to proceed with one narrative over another can also be understood as the decision to refine plans in such a way as to arrive at the chosen narrative • In the case of certainty, the desired narrative can be reached through the semilattice of plans with probability 1

Planning under uncertainty • In general, planners and decision makers make mistakes or ‘trembles’ when determining what to do – especially in organisations • The problem then becomes one of how best to allocate decision making resources throughout the organisation to maximise the expected value of narratives

The planner’s problem

Why firms exist • Firms exist when the expected rate of return to organising or coordinating the selection of narratives is greater than the cost of capital • If we let V(z) = the maximum value function for the above problem, and r is the cost of capital, then a firm exists if d. V(z)/dz > r. • This is a ‘Williamsonian’ explanation of the existence of firms – hierarchy outperforms the market

Incremental versus radical change • The application of Kuhn-Tucker to the problem of hierarchical organisation naturally presupposes the usual convexity conditions • If these are not satisfied – so that there are, say, increasing returns to investments of z in parts of the semilattice – then it may pay to forgo incremental improvements in organisational behaviour to secure discontinuous or discrete improvements (Hammer & Champy)

Volatility and planning • increases in the volatility of the operating environment of firms mean that top-down, high-level strategic planning is made otiose, and that strategic resources ought to be allocated closer to the coal face (Mintzberg). • This is demonstrated by way of a rather contrived construct

Mean preserving semilattices • A semilattice is said to be mean preserving if for any two distinct terminal nodes, j′ and j″: • and is mean dispersing otherwise.

Examples of semilattice types An example of a mean preserving semilattice is the following: An example of a mean dispersing semilattice is the following:

Investing in decision making • It can then be shown that, in mean preserving semilattices, it certainly pays to allocate management resource to the lowest decision nodes, whilst this is not true for mean dispersing semilattice • This is suggestive of the intuitive conclusion that the more entropic the environment the greater should be the local allocation of recourses

Conclusions • We have put forward a new model of agency • This is a model of hierarchical planning • This model has a natural application to organisations and firms • The model allows us to unify various propositions from theory of the firm into a single analytical framework • The model is immature • There is plenty of potential for further work