Prerequisites Almost essential Firm Basics THE FIRM OPTIMISATION

Prerequisites Almost essential Firm: Basics THE FIRM: OPTIMISATION MICROECONOMICS Principles and Analysis Frank Cowell April 2018 Frank Cowell: Firm Optimization 1

Overview Firm: Optimisation The setting Approaches to the firm’s optimisation problem Stage 1: Cost Minimisation Stage 2: Profit maximisation April 2018 Frank Cowell: Firm Optimization 2

The optimisation problem § We set up and solve a standard optimisation problem • make a quick list of its components • look ahead to the way we will do it for the firm § Objectives - Profit maximisation? § Constraints - Technology; other § Method - 2 -stage optimisation April 2018 Frank Cowell: Firm Optimization 3

Construct the objective function § Use info on prices and on quantities to build objective function wi • price of input i zi • amount of input i p • price of output q • amount of output • summed over all m inputs • subtract Cost from Revenue to get April 2018 Frank Cowell: Firm Optimization 4

Optimisation: the standard approach § Choose q and z to maximise m P : = pq – wizi i=1 §. . . subject to the production constraint. . . q (z) §. . and some obvious constraints: q 0 April 2018 z 0 • Could also write this as z Z(q) • You can’t have negative output or negative inputs Frank Cowell: Firm Optimization 5

A standard optimisation method § If is differentiable… § Set up a Lagrangian to take care of the constraints L (. . . ) necessity L (. . . ) = 0 z § Write down the First Order Conditions (FOC) § Check out second-order sufficiency conditions § Use FOC to characterise solution April 2018 2 2 L (. . . ) z z* = … Frank Cowell: Firm Optimization 6

Uses of FOC § First order conditions are crucial § Used over and over again in optimisation problems § For example: • characterising efficiency • analysing “Black box” problems • describing the firm's reactions to its environment § More of that in the next presentation § Right now a word of caution. . . April 2018 Frank Cowell: Firm Optimization 7

A word of warning § We’ve just argued that using FOC is useful • But sometimes it will yield ambiguous results • Sometimes it is undefined • Depends on the shape of the production function § You have to check whether it’s appropriate to apply the Lagrangian method § You may need to use other ways of finding an optimum April 2018 Frank Cowell: Firm Optimization 8

A way forward § We could just go ahead and solve the maximisation problem § But it makes sense to break it down into two stages • The analysis is a bit easier • You see how to apply optimisation techniques • It gives some important concepts that we can re-use later § First stage is “minimise cost for a given output level” • If you have fixed the output level q… • …then profit max is equivalent to cost min § Second stage is “find the output level to maximise profits” • Follows the first stage naturally • Uses the results from the first stage § We deal with stage each in turn April 2018 Frank Cowell: Firm Optimization 9

Overview Firm: Optimisation The setting A fundamental multivariable problem with a brilliant solution Stage 1: Cost Minimisation Stage 2: Profit maximisation April 2018 Frank Cowell: Firm Optimization 10

Stage 1 optimisation § Pick a target output level q § Take as given the market prices of inputs w § Maximise profits. . . §. . . by minimising costs m w i zi i=1 April 2018 Frank Cowell: Firm Optimization 11

A useful tool § For a given set of input prices w. . . § …the isocost is the set of points z in input space. . . §. . . that yield a given level of factor cost § These form a hyperplane (straight line). . . §. . . because of the simple expression for factor-cost structure April 2018 Frank Cowell: Firm Optimization 12

Isocost lines z 2 g n i as § Diagonal line: set of points where cost of input is c, a constant t s o c § One such “isocost” line for each value of the constant c § Arrow: indicates the order of the isocost lines e r c in w 1 z 1 + w 2 z 2 = c" w 1 z 1 + w 2 z 2 = c' w 1 z 1 + w 2 z 2 = c z 1 April 2018 Use this to derive optimum Frank Cowell: Firm Optimization 13

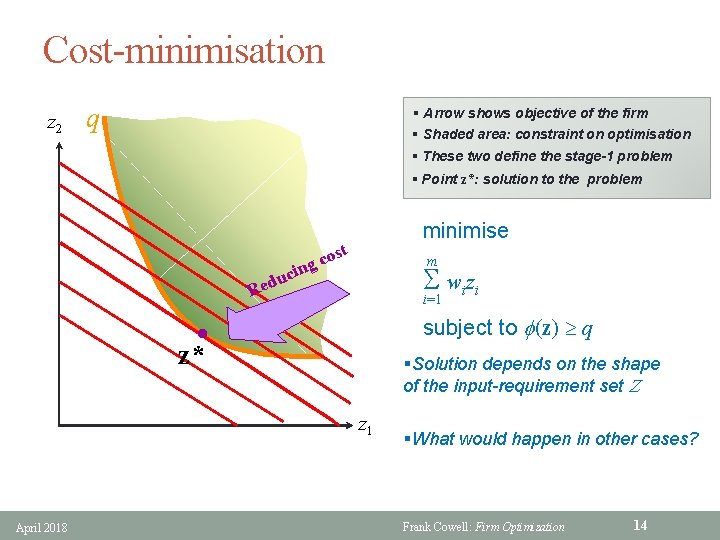
Cost-minimisation z 2 q § Arrow shows objective of the firm § Shaded area: constraint on optimisation § These two define the stage-1 problem § Point z*: solution to the problem minimise st co g n i m w i zi c u Red i=1 subject to (z) q l z* §Solution depends on the shape of the input-requirement set Z z 1 April 2018 §What would happen in other cases? Frank Cowell: Firm Optimization 14

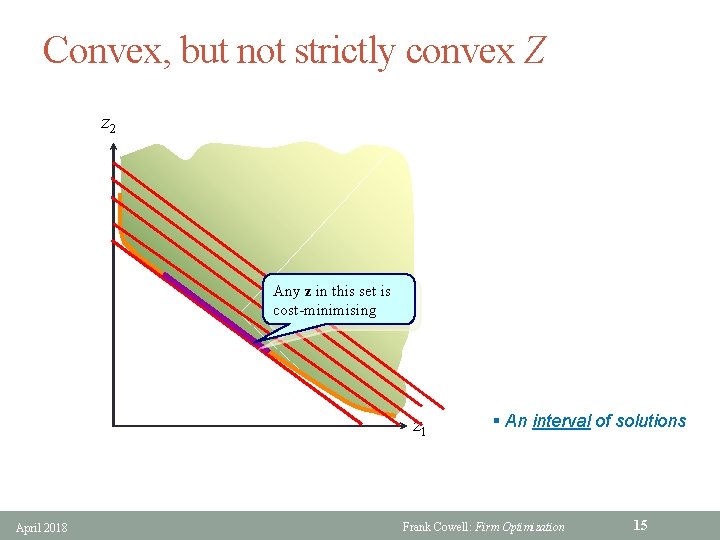
Convex, but not strictly convex Z z 2 Any z in this set is cost-minimising z 1 April 2018 § An interval of solutions Frank Cowell: Firm Optimization 15

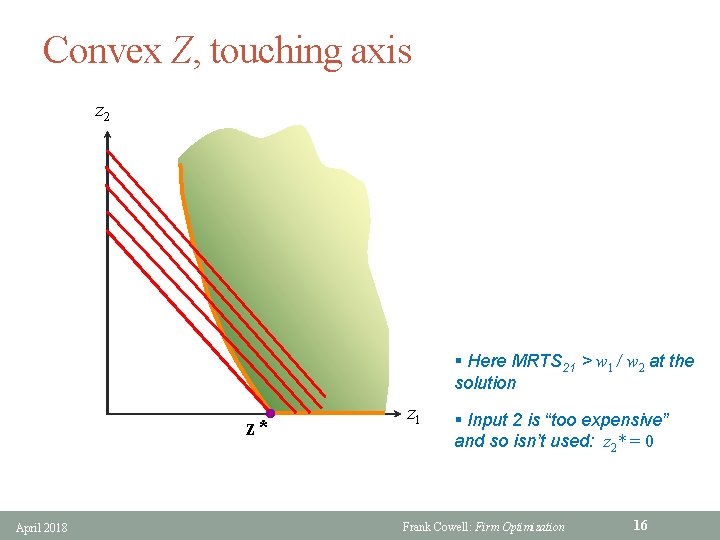
Convex Z, touching axis z 2 § Here MRTS 21 > w 1 / w 2 at the solution l z* April 2018 z 1 § Input 2 is “too expensive” and so isn’t used: z 2* = 0 Frank Cowell: Firm Optimization 16

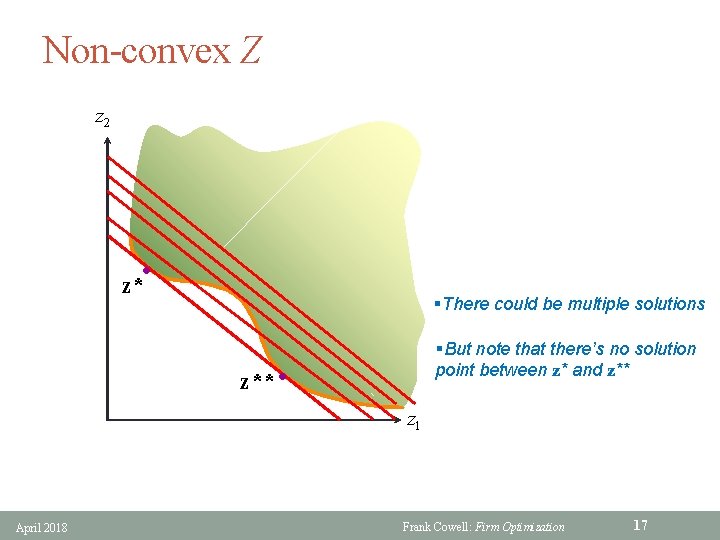
Non-convex Z z 2 l z* §There could be multiple solutions §But note that there’s no solution point between z* and z** l z 1 April 2018 Frank Cowell: Firm Optimization 17

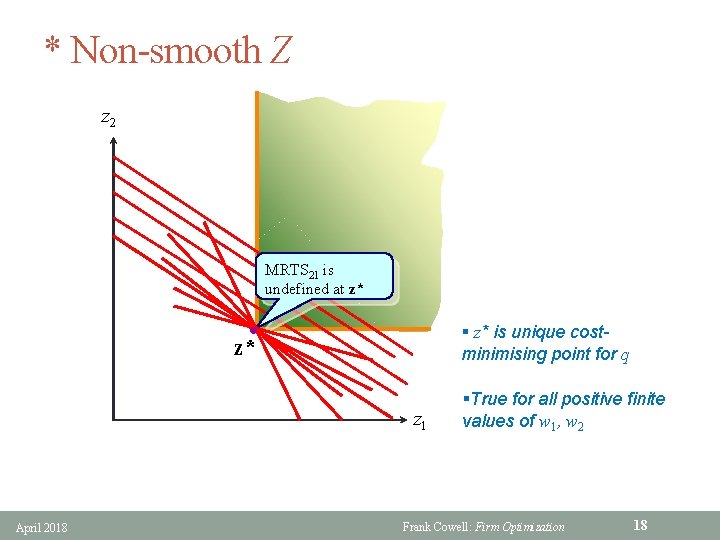
* Non-smooth Z z 2 MRTS 21 is undefined at z* § z* is unique costminimising point for q l z* z 1 April 2018 §True for all positive finite values of w 1, w 2 Frank Cowell: Firm Optimization 18

Cost-minimisation: strictly convex Z Lagrange multiplier § Minimise m w i zi i=1 q – (z)] (z) + l[q § Use the objective function §. . . and output constraint §. . . to build the Lagrangian § Differentiate w. r. t. z 1, . . . , zm ; set equal to 0 §. . . and w. r. t l § Because of strict convexity we have § Denote cost minimising values by an interior solution § A set of m+1 First-Order Conditions l* 1 (z* ) = w 1 l* 2 (z*) = w 2 … … … l* m(z *) = wm q = (z*) April 2018 ü ý þ one for each input output constraint Frank Cowell: Firm Optimization 19 *

If isoquants can touch the axes. . . § Minimise m w i zi i=1 + l [q – f(z)] § Now there is the possibility of corner solutions § A set of m+1 First-Order Conditions l*f 1 (z*) w 1 l*f 2 (z*) w 2 … … … l*fm(z*) wm ü ý þ q = f(z*) April 2018 Interpretation Can get “<” if optimal value of this input is 0 Frank Cowell: Firm Optimization 20

From the FOC § If both inputs i and j are used and MRTS is defined then. . . i(z*) wi ——— = — * j(z ) wj § MRTS = input price ratio § If input i could be zero then. . . i(z*) wi ——— — * j(z ) wj § MRTSji input price ratio § “implicit” price = market price § “implicit” price market price Solution April 2018 Frank Cowell: Firm Optimization 21

The solution. . . § Solving the FOC, you get a cost-minimising value for each input. . . zi* = Hi(w, q) §. . . for the Lagrange multiplier l* = l*(w, q) §. . . and for the minimised value of cost itself. § The cost function is defined as C(w, q) : = min S wi zi { (z) q} vector of input prices April 2018 Specified output level Frank Cowell: Firm Optimization 22

Interpreting the Lagrange multiplier § The solution function: C(w, q) = iwi zi* = i wi zi*– l* [ (z*) – q] § Differentiate with respect to q: Cq(w, q) = i iwi. H q(w, q) * i i i(z ) H q(w, – l * [ § Rearrange: At the optimum, either the constraint binds or the Lagrange multiplier is zero Express demands in terms of (w, q) q) – 1] Vanishes because of FOC l * i(z*) = wi Cq(w, q) = i [wi – l* i(z*)] Hiq(w, q) + l* Lagrange multiplier in the stage 1 problem is just marginal cost Cq (w, q) = l* § Result is just an applications of a general “envelope” theorem § It holds for the untransformed, original version of the problem § If we use a transformed version of the constraint (for example log q log (z)) we get a different Lagrange multiplier) April 2018 Frank Cowell: Firm Optimization 23

The cost function is an amazingly useful concept § Because it is a solution function. . . §. . . it automatically has very nice properties § These are true for all production functions § And they carry over to applications other than the firm § We’ll investigate these graphically April 2018 Frank Cowell: Firm Optimization 24

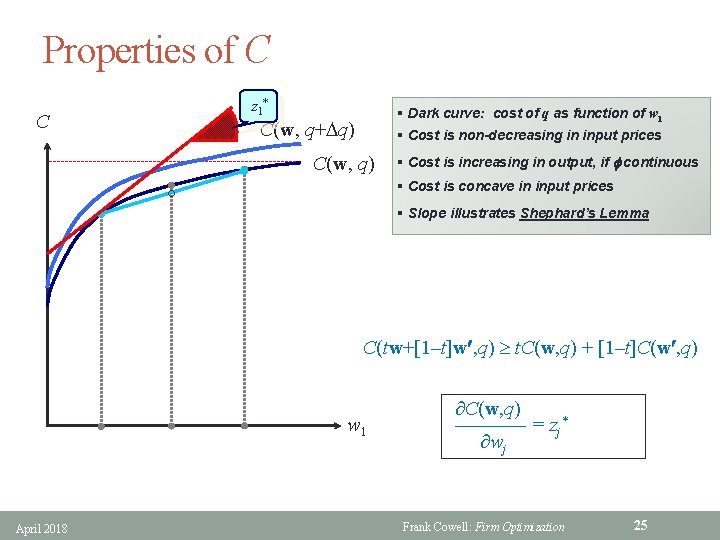
Properties of C z 1* C § Dark curve: cost of q as function of w 1 § Cost is non-decreasing in input prices C(w, q+ q) C(w, q) § Cost is increasing in output, if f continuous § Cost is concave in input prices ° § Slope illustrates Shephard’s Lemma C(tw+[1–t]w , q) t. C(w, q) + [1–t]C(w , q) w 1 April 2018 C(w, q) ———— = zj* wj Frank Cowell: Firm Optimization 25

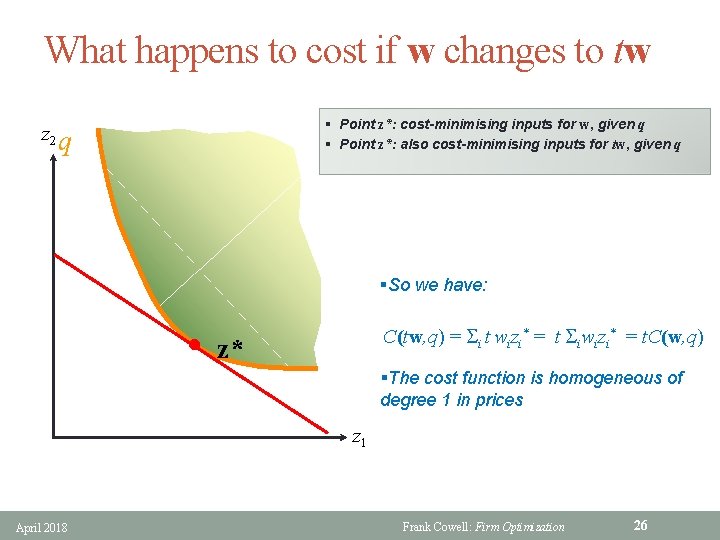
What happens to cost if w changes to tw z 2 § Point z*: cost-minimising inputs for w, given q § Point z*: also cost-minimising inputs for tw, given q q §So we have: • C(tw, q) = i t wizi* = t iwizi* = t. C(w, q) z* §The cost function is homogeneous of degree 1 in prices z 1 April 2018 Frank Cowell: Firm Optimization 26

Cost Function: 5 things to remember § Non-decreasing in every input price • Increasing in at least one input price § Increasing in output § Concave in prices § Homogeneous of degree 1 in prices § Shephard's Lemma April 2018 Frank Cowell: Firm Optimization 27

Example Production function: q z 10. 1 z 20. 4 Equivalent form: log q 0. 1 log z 1 + 0. 4 log z 2 Lagrangian: w 1 z 1 + w 2 z 2 + l [log q – 0. 1 log z 1 – 0. 4 log z 2] FOCs for an interior solution: w 1 – 0. 1 l / z 1 = 0 w 2 – 0. 4 l / z 2 = 0 log q = 0. 1 log z 1 + 0. 4 log z 2 From the FOCs: log q = 0. 1 log (0. 1 l / w 1) + 0. 4 log (0. 4 l / w 2 ) l = 0. 1– 0. 2 0. 4– 0. 8 w 10. 2 w 20. 8 q 2 Therefore, from this and the FOCs: w 1 z 1 + w 2 z 2 = 0. 5 l = 1. 649 w 10. 2 w 20. 8 q 2 April 2018 Frank Cowell: Firm Optimization 28

Overview Firm: Optimisation The setting …using the results of stage 1 Stage 1: Cost Minimisation Stage 2: Profit maximisation April 2018 Frank Cowell: Firm Optimization 29

Stage 2 optimisation § Take the cost-minimisation problem as solved § Take output price p as given • Use minimised costs C(w, q) • Set up a 1 -variable maximisation problem § Choose q to maximise profits § First analyse components of the solution graphically • Tie-in with properties of the firm (in the previous presentation) § Then we come back to the formal solution April 2018 Frank Cowell: Firm Optimization 30

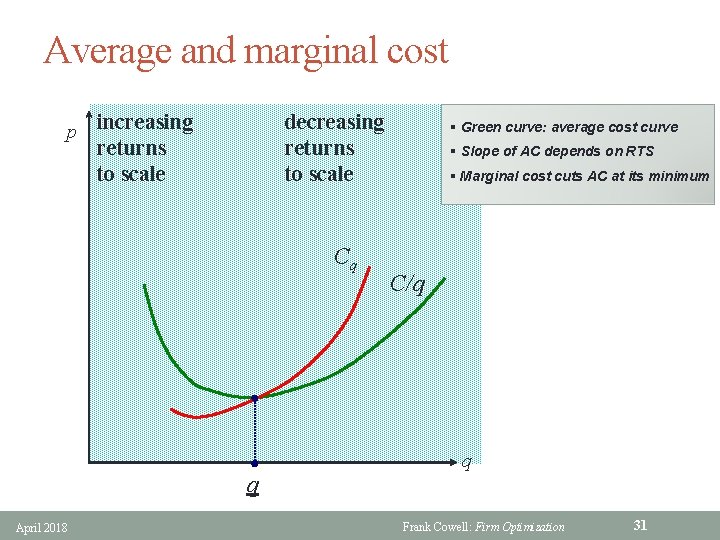
Average and marginal cost p increasing returns to scale decreasing returns to scale Cq q April 2018 § Green curve: average cost curve § Slope of AC depends on RTS § Marginal cost cuts AC at its minimum C/q q Frank Cowell: Firm Optimization 31

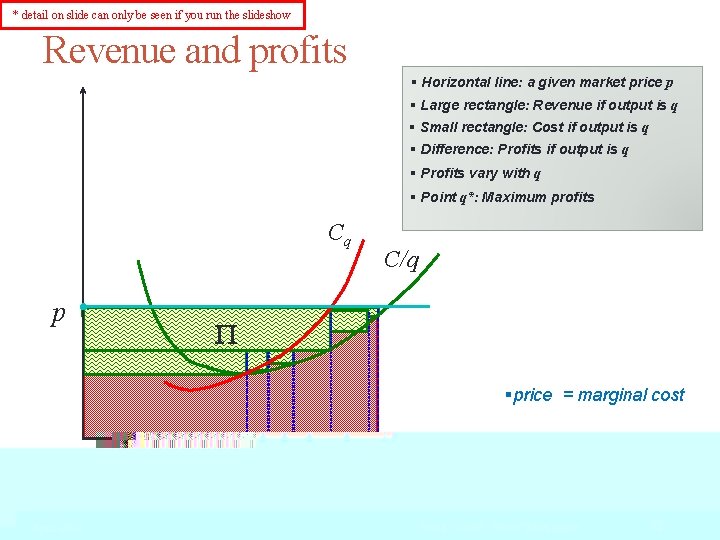
* detail on slide can only be seen if you run the slideshow Revenue and profits § Horizontal line: a given market price p § Large rectangle: Revenue if output is q § Small rectangle: Cost if output is q § Difference: Profits if output is q § Profits vary with q § Point q*: Maximum profits Cq p C/q P §price = marginal cost q q q April 2018 q q* Frank Cowell: Firm Optimization 32

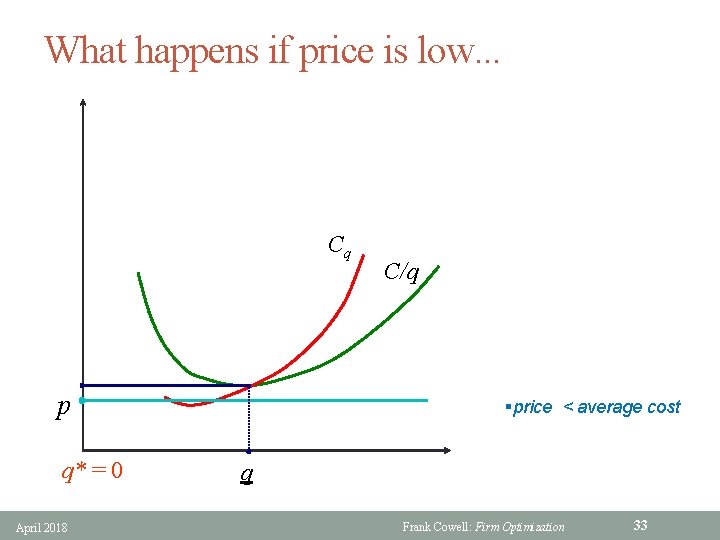
What happens if price is low. . . Cq p q* = 0 April 2018 C/q §price < average cost q Frank Cowell: Firm Optimization 33

Profit maximisation § Objective is to choose q to max: pq – C (w, q) § From the First-Order Conditions if q* > 0: p = Cq (w, q*) C(w, q*) p ———— q* § In general: pq* C(w, q*) April 2018 “Revenue minus minimised cost” “Price equals marginal cost” “Price covers average cost” covers both the cases: q* > 0 and q* = 0 Frank Cowell: Firm Optimization 34

Example (continued) Production function: q z 10. 1 z 20. 4 Resulting cost function: C(w, q) = 1. 649 w 10. 2 w 20. 8 q 2 Profits: pq – C(w, q) = pq – A q 2 where A: = 1. 649 w 10. 2 w 20. 8 FOC: p – 2 Aq = 0 Result: q = p / 2 A = 0. 3031 w 1– 0. 2 w 2– 0. 8 p April 2018 Frank Cowell: Firm Optimization 35

Summary § Key point: Profit maximisation can be viewed in two stages: • Stage 1: choose inputs to minimise cost • Stage 2: choose output to maximise profit § What next? Use these to predict firm's reactions April 2018 Frank Cowell: Firm Optimization 36