Statistics Econometrics Statistics Econometrics Statistics Econometrics Statistics for

Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics Statistics for Economist Chap 7. The Error for Regression 1. 2. 3. 4. 5. Difference between Actual and Predict values Computing RMSE Using the Correlation. The Residual Plot The Vertical Strips Approximating to the Normal Curve Inside a Vertical Strip Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics

INDEX STATISTICS 1 Difference between Actual and Predict Values 2 Computing RMSE Using the Correlation 3 The Residual Plot 4 The Vertical Strips 5 Approximating to the Normal Curve Inside a Vertical Strip Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 2

STATISTICS 1. Difference between Actual and Predict Values Root-Mean-Square-Error (RMSE) Error Actual value Root-Mean-Square Error (RMSE) Standard Error of Estimate Standard Error of Regression 회귀직선 Estimate Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 3

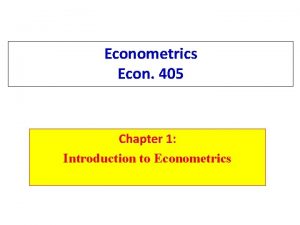
STATISTICS 1. Difference between Actual and Predict Values Estimation error 1 Korean men 4514 with age 10 -90 - Average height = 167. 5 cm height 141 cm. average weight of height 141 cm is 38. 7 kg - SD of height = 8. 5 cm residual = actual weight – predicted weight - SD of weight = 11. 9 kg = 54. 5 kg – 38. 7 kg = +15. 8 kg - Average weight = 63. 5 kg - Correlation coefficient = 0. 67 Residual of A Residual of B 67. 4 kg – 84. 0 kg = -16. 6 kg Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 4

STATISTICS 1. Difference between Actual and Predict Values Estimation error 2 Estimation error • actual weight – predicted weight • generally called, residual. • The overall size of these errors in measured by taking their root mean square. weight error actual predicted Vertical distance from the line height Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 5

1. Difference between Actual and Predict Values STATISTICS Computing the RMSE meaning • A typical point on a scatter plot is above or below the regression line by 8. 9 kg. (vertical distance) The divisor • degrees of freedom = 4514 -2 = 4512 Computing the errors are based on the regression line. The regression line is defined by slope and intercept (lowering the degree of freedom) Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 6

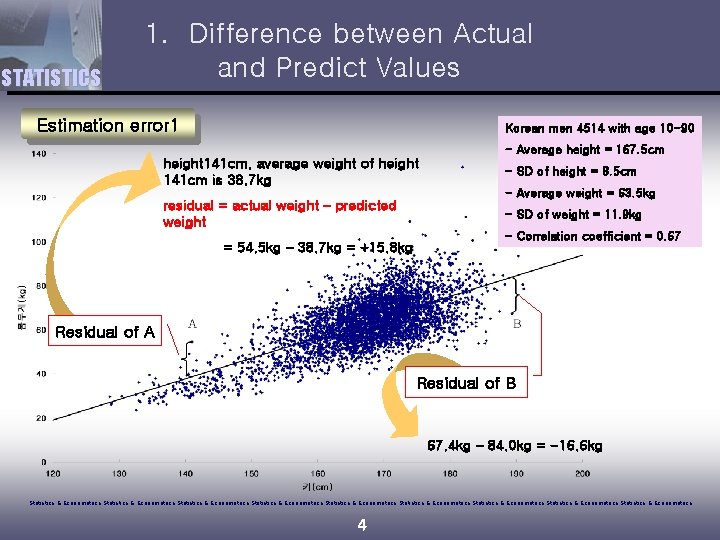
STATISTICS 1. Difference between Actual and Predict Values Regression line & RMSE vs. Average & SD The Normal curve. Following 68 -95 rule. Group average height of the regression line Distance from the center(RMSE) Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 7

STATISTICS 1. Difference between Actual and Predict Values Regression and rule of thumb 2 RMSE 1 RMSE regression 68% 1 RMSE regression 2 RMSE 95% About 68% of the points on a scatter diagram will be within 1 RMSE of the regression line; about 95% of them will be within 2 RMSE. Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 8

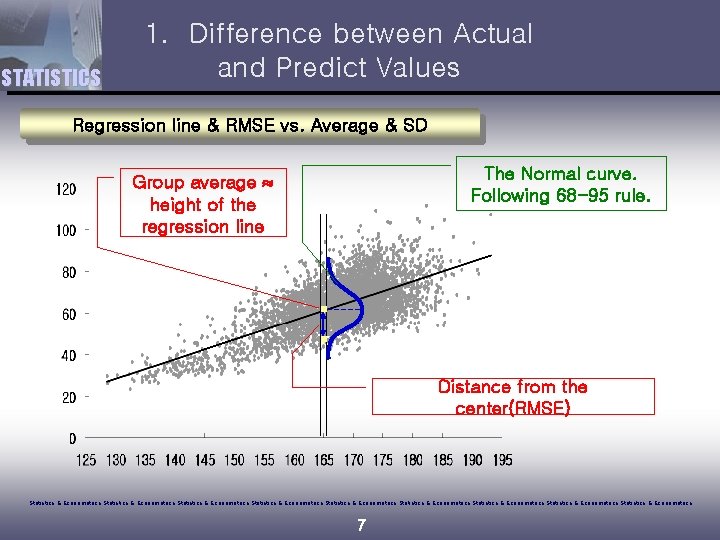
STATISTICS 1. Difference between Actual and Predict Values Elementary method for RMSE y residual= (actual y) – (average y) actual estimate = (average y) x Estimate y ignoring x → a horizontal line for estimates. This elementary RMSE is SDy. Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 9

INDEX STATISTICS 1 Difference between Actual and Predict Values 2 Computing RMSE Using the Correlation 3 The Residual Plot 4 The Vertical Strips 5 Approximating to the Normal Curve Inside a Vertical Strip Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 10

2. Computing RMSE Using the Correlation STATISTICS RMSE of the regression line and SDy y y Regression lines Average y RMSE SDy x x r=1 RMSE of regression is about Degrees of freedom RMSE of regression < SDy → RMSE = 0 r = -1 → RMSE = 0 r=0 → RMSE SDy because the regression line get closer to the points than the horizontal line. ref: Regression line is for ‘much closer to the more scatters’. Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 11

2. Computing RMSE Using the Correlation STATISTICS RMSE and Correlation coefficient RMSE Measures vertically spread around Correlation coefficient the regression line Measures spread relative to the SD in absolute y-terms. without units. We can get the RMSE from SDy using the correlation coefficient. . Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 12

2. Computing RMSE Using the Correlation STATISTICS Regression analysis and correlation coefficient Ø r describes the clustering of the points around the SD line, relative to the SDs Ø Associated with each 1 SD increase in x there is an increase of only r SDs in y, on the average Ø r determines the accuracy of the regression predictions, through the formula RMSE = Ø SDy. RMSE describes how the regression line summarize data well. Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 13

INDEX STATISTICS 1 Difference between Actual and Predict Values 2 Computing RMSE Using the Correlation 3 The Residual Plot 4 The Vertical Strips 5 Approximating to the Normal Curve Inside a Vertical Strip Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 14

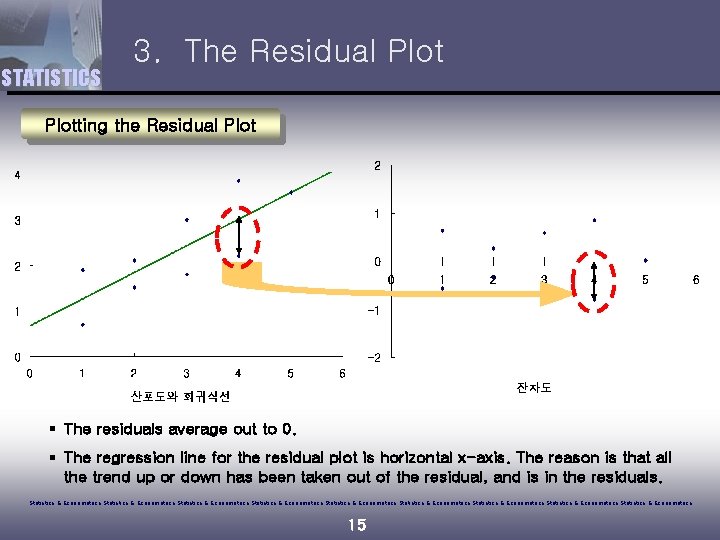
STATISTICS 3. The Residual Plotting the Residual Plot § The residuals average out to 0. § The regression line for the residual plot is horizontal x-axis. The reason is that all the trend up or down has been taken out of the residual, and is in the residuals. Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 15

STATISTICS 3. The Residual Plot A residual with a strong pattern With a mistake to use a regression line, such a pattern appears. The residual plot should not have a strong pattern. Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 16

INDEX STATISTICS 1 Difference between Actual and Predict Values 2 Computing RMSE Using the Correlation 3 The Residual Plot 4 The Vertical Strips 5 Approximating to the Normal Curve Inside a Vertical Strip Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 17

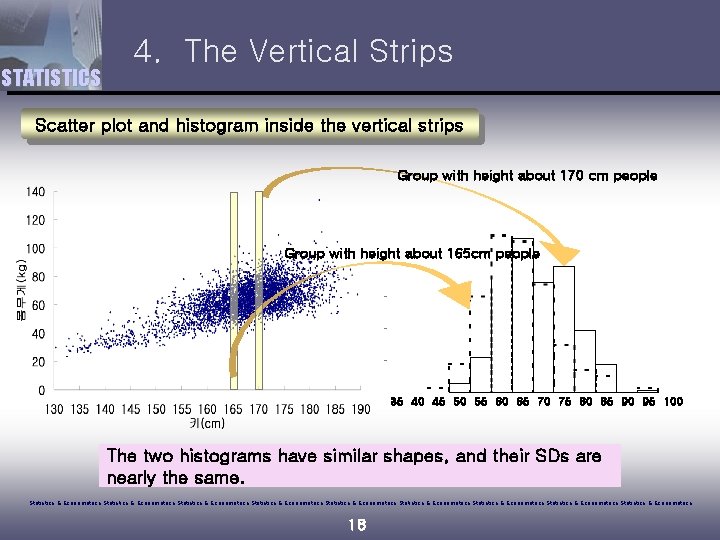
STATISTICS 4. The Vertical Strips Scatter plot and histogram inside the vertical strips Group with height about 170 cm people Group with height about 165 cm people 35 40 45 50 55 60 65 70 75 80 85 90 95 100 The two histograms have similar shapes, and their SDs are nearly the same. Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 18

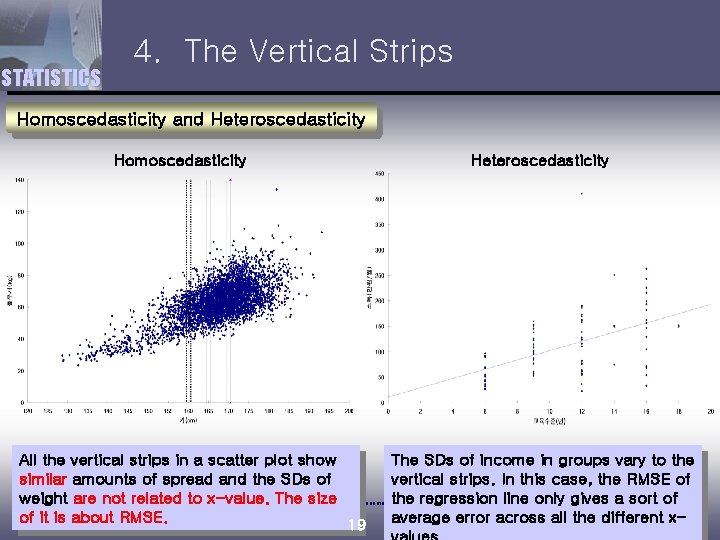
STATISTICS 4. The Vertical Strips Homoscedasticity and Heteroscedasticity Homoscedasticity All the vertical strips in a scatter plot show similar amounts of spread and the SDs of weight are not related to x-value. The size of it is about RMSE. 19 Heteroscedasticity The SDs of income in groups vary to the vertical strips. In this case, the RMSE of the regression line only gives a sort of average error across all the different x- Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics

INDEX STATISTICS 1 Difference between Actual and Predict Values 2 Computing RMSE Using the Correlation 3 The Residual Plot 4 The Vertical Strips 5 Approximating to the Normal Curve Inside a Vertical Strip Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 20

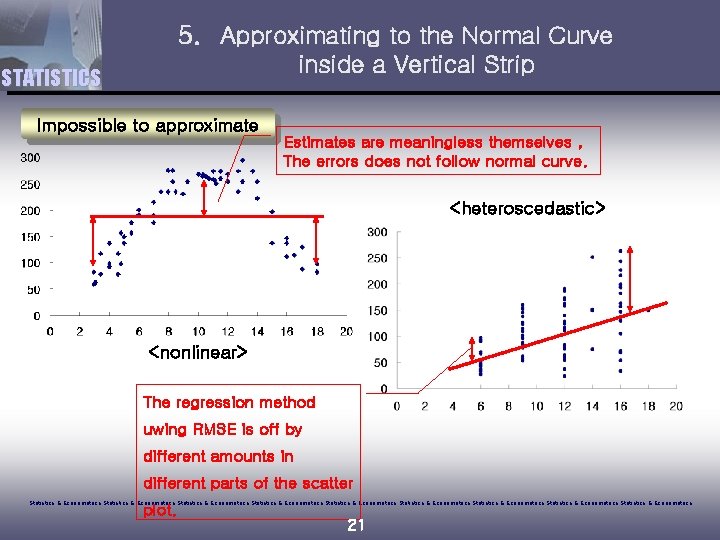
5. Approximating to the Normal Curve inside a Vertical Strip STATISTICS Impossible to approximate Estimates are meaningless themselves , The errors does not follow normal curve. <heteroscedastic> <nonlinear> The regression method uwing RMSE is off by different amounts in different parts of the scatter Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics plot. 21

STATISTICS 5. Approximating to the Normal Curve inside a Vertical Strip example 1 Ex) Midterm and final scores of econometrics in spring semester year 2002 midterm average = 27. 9 final average = 56. 4 r = 0. 49 midterm SD = 8. 5 final SD = 13. 8 an oval shaped scatter plot. (1) What percentage of students got 66 or over on the final? (2) What percentage of students whose midterm score is 33 got 66 or over on the final? Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 22

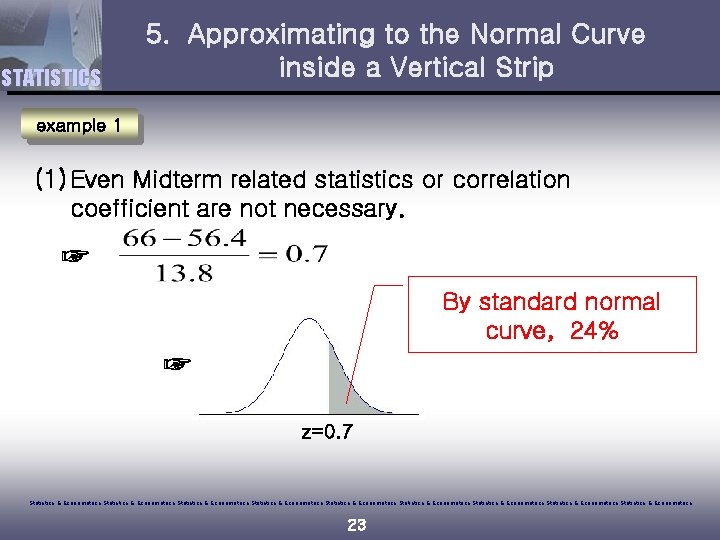
STATISTICS 5. Approximating to the Normal Curve inside a Vertical Strip example 1 (1) Even Midterm related statistics or correlation coefficient are not necessary. ☞ By standard normal curve, 24% ☞ z=0. 7 Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 23

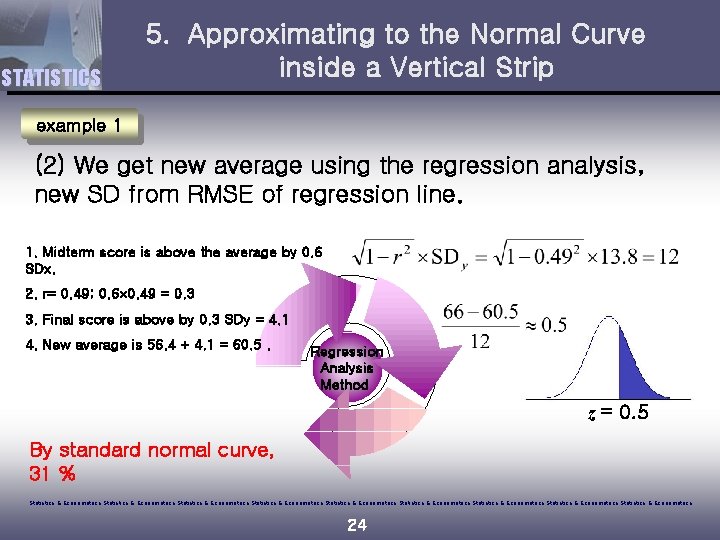
STATISTICS 5. Approximating to the Normal Curve inside a Vertical Strip example 1 (2) We get new average using the regression analysis, new SD from RMSE of regression line. 1. Midterm score is above the average by 0. 6 SDx. 2. r= 0. 49; 0. 6 0. 49 = 0. 3 3. Final score is above by 0. 3 SDy = 4. 1 4. New average is 56. 4 + 4. 1 = 60. 5. Regression Analysis Method z = 0. 5 By standard normal curve, 31 % Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 24