Statistics Econometrics Statistics Econometrics Statistics Econometrics Statistics for

Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics Statistics for Economist Chap 6. Regression 1. 2. 3. 4. 5. The Relation of Two Variables The Graph of Averages The Regression Method The Regression Effect The Regression Line for x on y and y on x Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics

STATISTICS INDEX 1 The Relation of Two Variables 2 The Graph of Averages 3 The Regression Method 4 The Regression Effect 5 The Regression Line for x on y and y on x Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 2

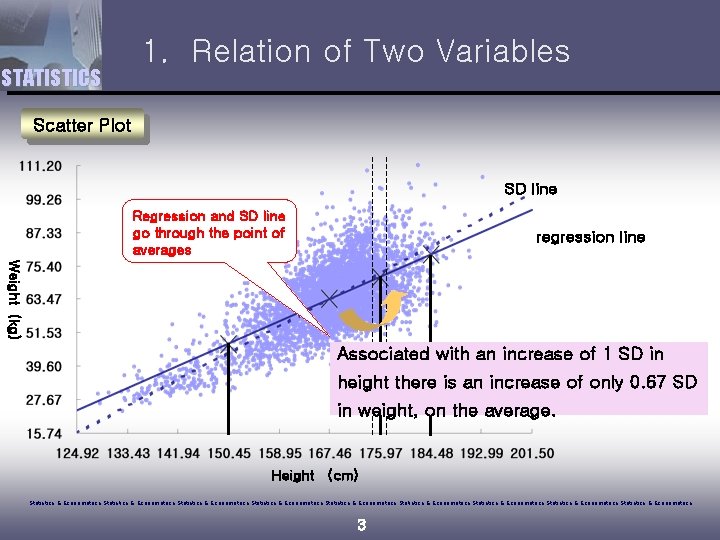
STATISTICS 1. Relation of Two Variables Scatter Plot SD line Regression and SD line go through the point of averages regression line Weight (kg) Associated with an increase of 1 SD in height there is an increase of only 0. 67 SD in weight, on the average. Height (cm) Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 3

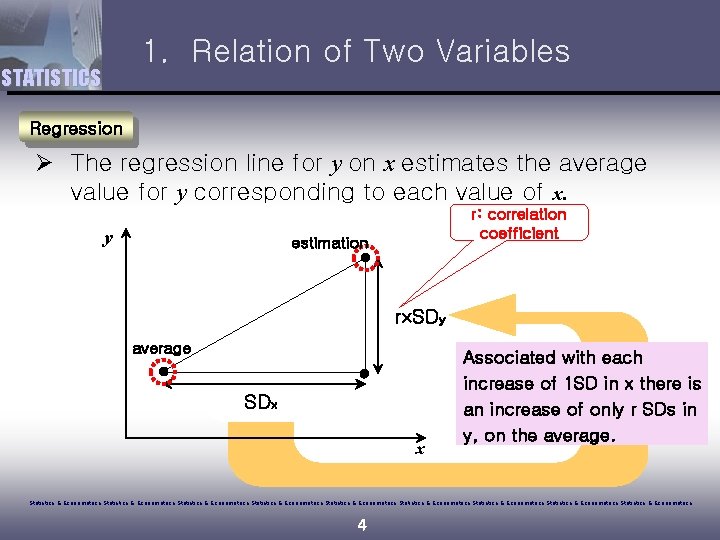
1. Relation of Two Variables STATISTICS Regression Ø The regression line for y on x estimates the average value for y corresponding to each value of x. y r: correlation coefficient estimation r SDy average SDx x Associated with each increase of 1 SD in x there is an increase of only r SDs in y, on the average. Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 4

STATISTICS INDEX 1 The Relation of Two Variables 2 The Graph of Averages 3 The Regression Method 4 The Regression Effect 5 The Regression Line for x on y and y on x Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 5

STATISTICS 2. Graph of Averages regression Graph of averages 각 점들은 각각의 키에 대하여 그 키에 해당하는 집단 의 평균 몸무게를 보여준다. 점 위에 표시된 숫자는 해당집단의 크기를 나타낸다. Many points on the graph of averages are near the line. This line is regression line. Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 6

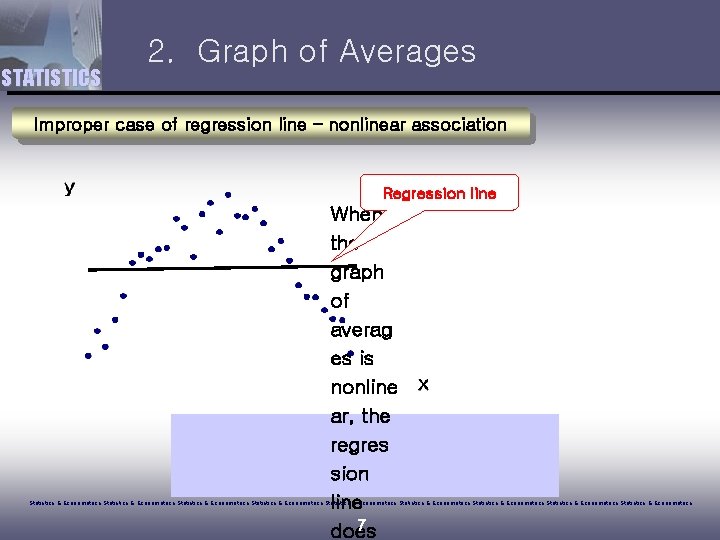
STATISTICS 2. Graph of Averages Improper case of regression line – nonlinear association Regression line When the graph of averag es is nonline ar, the regres sion line 7 does Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics

STATISTICS INDEX 1 The Relation of Two Variables 2 The Graph of Averages 3 The Regression Method 4 The Regression Effect 5 The Regression Line for x on y and y on x Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 8

STATISTICS 3. Regression Method Guess the weight <Health and Nutrition weight (kg) Examination Survey> Without being told anything else about him, the best guess on the weight of one of these men is the overall average weight 63. 5 kg. If you are told the man’s height: 179. 5 cm then your best guess for his weight is the average for all the 179. 5 cm men in the study , 74. 7 kg. height(cm) Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 9

STATISTICS 3. Regression Method Example 1 ØFollowings are the results of 100 students majoring in economics in a certain college. Economics 1 average = 3. 00 SDX = 0. 87 Statistics average = 2. 80 SDY = 0. 86 r = 0. 36 EX) Predict the statistics GPA of a student whose GPA of Economics I is 3. 70. Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 10

3. Regression Method STATISTICS Example 1 Corr. coeff 2. 0. 36 0. 8 = 0. 29 SDy above average on the Statistics. 1. 0. 8 SDx above average 2. on the Economics 1. 3. 7 -3. 0 = 0. 7 = 0. 87 0. 8 SDX Regression Analysis 4. The predicted GPA of statistics is 2. 80 + 0. 25 = 3. 05 SDy 3. That is, 0. 29 0. 86 = 0. 25(GPA) above average on the Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 11

STATISTICS 3. Regression Method notice ☞ when estimating on new subjects, Foregoing data can represent the new subjects ; reasonable!! Foregoing data and the new subjects are different in groups or in the range ; you have to think about the issue carefully before applying the regression method. Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 12

STATISTICS 3. Regression Method In the case of [example 1] … Would be the data from the students majoring in Economics applied directly to Jane whose major is Philosophy? Ø What if Jane majors in Philosophy not in Economics? Ø What if Jane’s GPA of Economics I is 4. 3 but 3. 7? Ø If most GPAs of the Economics 1 (x-value) are between 2. 0 and 4. 0 , Jane’s x-value(4. 3) is out of the previous x-range. Would the estimated regression line based on the x- value range 2. 0~4. 0 be applied to Jane’s GPA which is over the range? Ø [The extrapolation is not a simple problem. ] Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 13

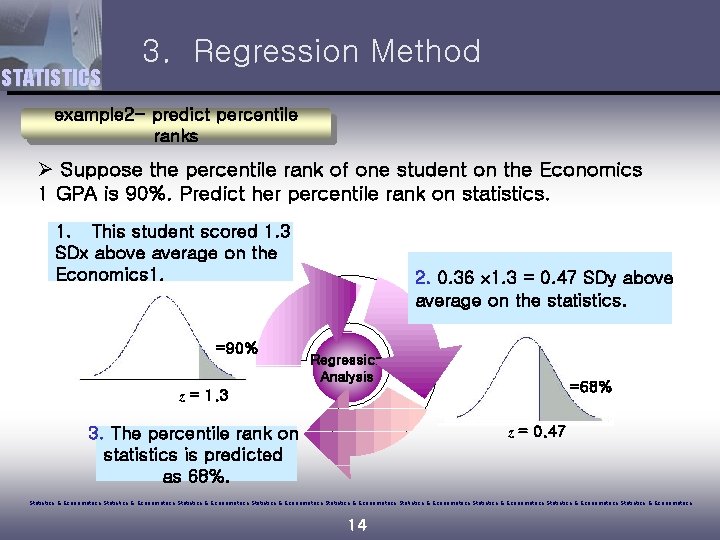
STATISTICS 3. Regression Method example 2 - predict percentile ranks Ø Suppose the percentile rank of one student on the Economics 1 GPA is 90%. Predict her percentile rank on statistics. 1. This student scored 1. 3 SDx above average on the Economics 1. =90% 2. 0. 36 1. 3 = 0. 47 SDy above average on the statistics. Regression Analysis =68% z = 1. 3 z = 0. 47 3. The percentile rank on statistics is predicted as 68%. Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 14

STATISTICS INDEX 1 The Relation of Two Variables 2 The Graph of Averages 3 The Regression Method 4 The Regression Effect 5 The Regression Line for x on y and y on x Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 15

STATISTICS 4. Regression Effect Y-values of points are spread symmetrically along the SD line overall. regression to mediocrity containing too many points with small x-value. Most of these points’ y-values are above the SD line. Containing too many points with large x-value. Most of these points’ y-values are below the SD line. Regression line SD line Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 16

STATISTICS 4. Regression Effect Regression effect Final average scores corresponding to each midterm scores Regression line – summarizes each average points well SD line Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 17

STATISTICS 4. Regression Effect regression fallacy Ø The regression effect occurs when each point representing data is spread out around the SD line. Ø The fallacy that the regression effect must be due to something important, not just the spread around the line ☞ Regression Fallacy Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 18

If so me one STATISTICS sc The model for regression effect ore Suppose that the probabilitys error is 5 with ab probability 0. 5. ove ave The people scored 140 can be divided into two rag groups with true score 135 eor 145. Observed score= 140 on the (observed score) = (true score) + (chance error) first tes t, 135 145 the tru e sc ore 19 is 4. Regression Effect Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics

STATISTICS INDEX 1 The Relation of Two Variables 2 The Graph of Averages 3 The Regression Method 4 The Regression Effect 5 The Regression Line for x on y and y on x Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 20

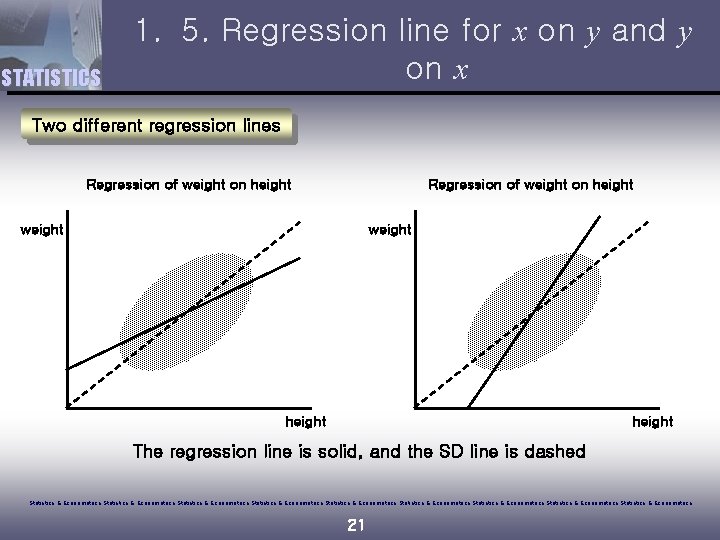
STATISTICS 1. 5. Regression line for x on y and y on x Two different regression lines Regression of weight on height weight height The regression line is solid, and the SD line is dashed Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 21

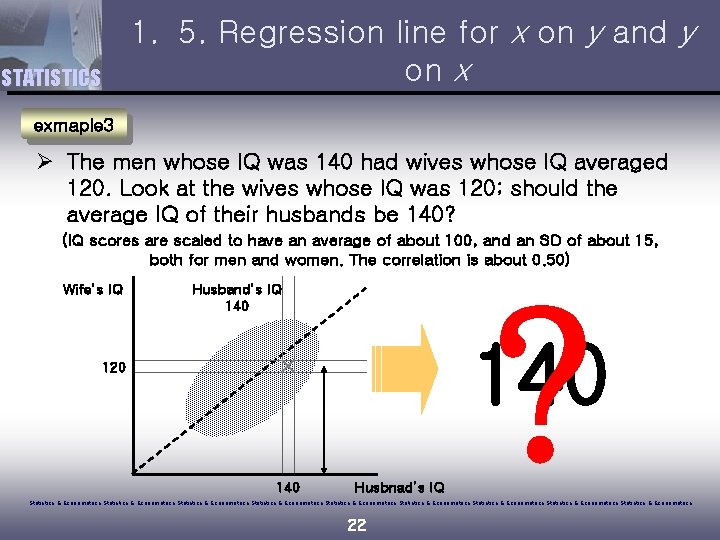
STATISTICS 1. 5. Regression line for x on y and y on x exmaple 3 Ø The men whose IQ was 140 had wives whose IQ averaged 120. Look at the wives whose IQ was 120; should the average IQ of their husbands be 140? (IQ scores are scaled to have an average of about 100, and an SD of about 15, both for men and women. The correlation is about 0. 50) Wife’s IQ Husband’s IQ 140 ? 140 120 140 Husbnad’s IQ Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 22

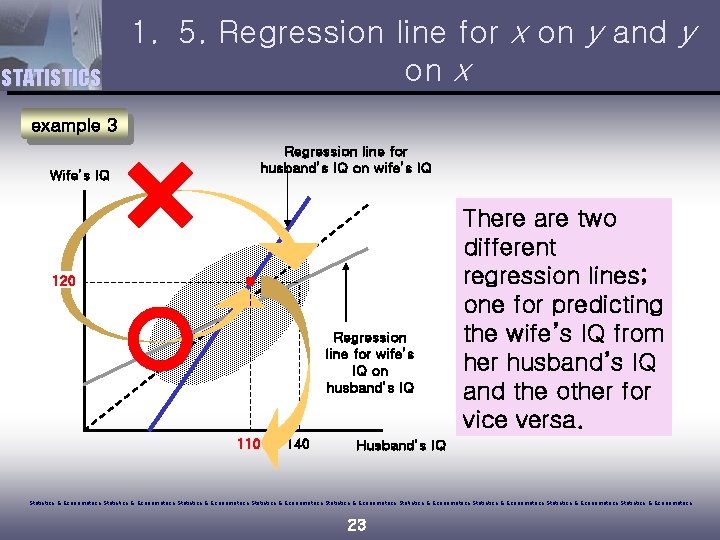
STATISTICS 1. 5. Regression line for x on y and y on x example 3 Wife’s IQ Regression line for husband’s IQ on wife’s IQ 120 Regression line for wife’s IQ on husband’s IQ 110 140 There are two different regression lines; one for predicting the wife’s IQ from her husband’s IQ and the other for vice versa. Husband’s IQ Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 23