Statistics Econometrics Statistics Econometrics Statistics Econometrics Statistics for

INDEX STATISTICS 1 The Law of Averages (Law of Large Numbers) 2 The Stochastic

1. The Law of Averages STATISTICS The Law of Averages (1) Head 100 is

1. The Law of Averages STATISTICS The Law of Averages (2) # of tosses

1. The Law of Averages STATISTICS The Law of Averages (3) As the number

1. The Law of Averages STATISTICS Ralative percentage of probability error The Law of

2. The Stochastic Processes STATISTICS Stochastic Process and Applying a Box Model • To

2. The Stochastic Processes STATISTICS The Stochastic Processes and Box Model at Inference :

STATISTICS 3. Making a Box Model Box of tickets box drawing tickets 25 draws

STATISTICS 3. Making a Box Model 1 2 3 4 5 6 1 What

STATISTICS 3. Making a Box Model Example A gambling problem in which the same

Slides: 13

Download presentation

Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics Statistics for Economist Ch. 11 The Law of Averages 1. The Law of Averages 2. (Law of Large Numbers) 2. The Stochastic Processes 3. Making a Box Model Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics

INDEX STATISTICS 1 The Law of Averages (Law of Large Numbers) 2 The Stochastic Processes 3 Making a Box Model Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 2

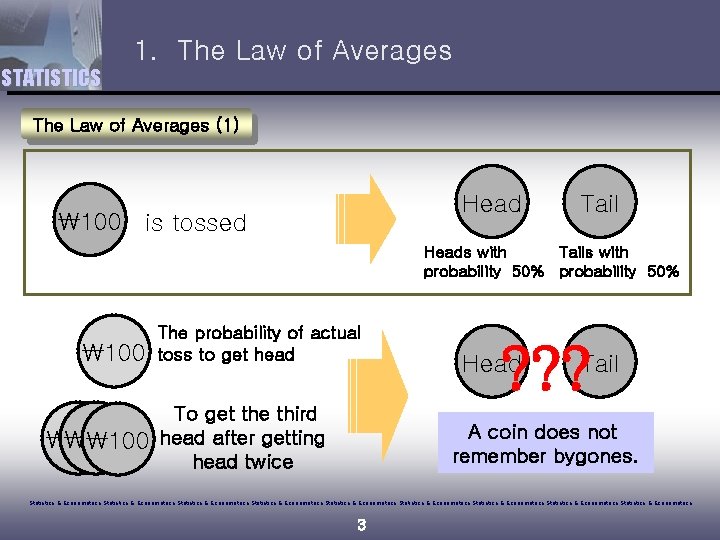
1. The Law of Averages STATISTICS The Law of Averages (1) Head 100 is tossed Tail Heads with Tails with probability 50% 100 The probability of actual toss to get head To get the third head after getting head twice ? ? ? Head Tail A coin does not remember bygones. Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 3

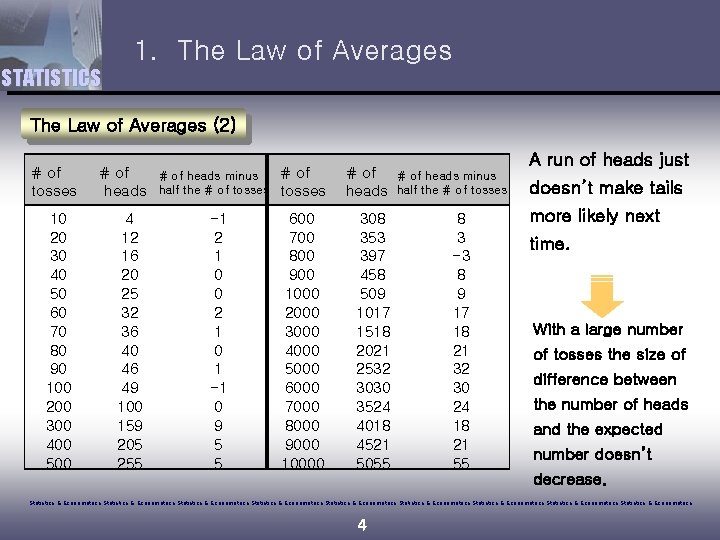
1. The Law of Averages STATISTICS The Law of Averages (2) # of tosses 10 20 30 40 50 60 70 80 90 100 200 300 400 500 # of heads 4 12 16 20 25 32 36 40 46 49 100 159 205 255 # of heads minus half the # of tosses -1 2 1 0 0 2 1 0 1 -1 0 9 5 5 # of tosses # of heads 600 700 800 900 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000 308 353 397 458 509 1017 1518 2021 2532 3030 3524 4018 4521 5055 A run of heads just # of heads minus half the # of tosses 8 3 -3 8 9 17 18 21 32 30 24 18 21 55 doesn’t make tails more likely next time. With a large number of tosses the size of difference between the number of heads and the expected number doesn’t decrease. Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 4

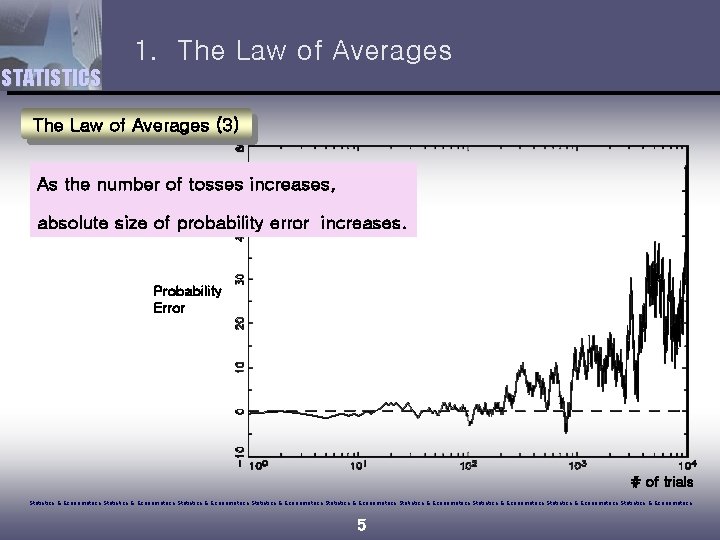
1. The Law of Averages STATISTICS The Law of Averages (3) As the number of tosses increases, absolute size of probability error increases. Probability Error # of trials Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 5

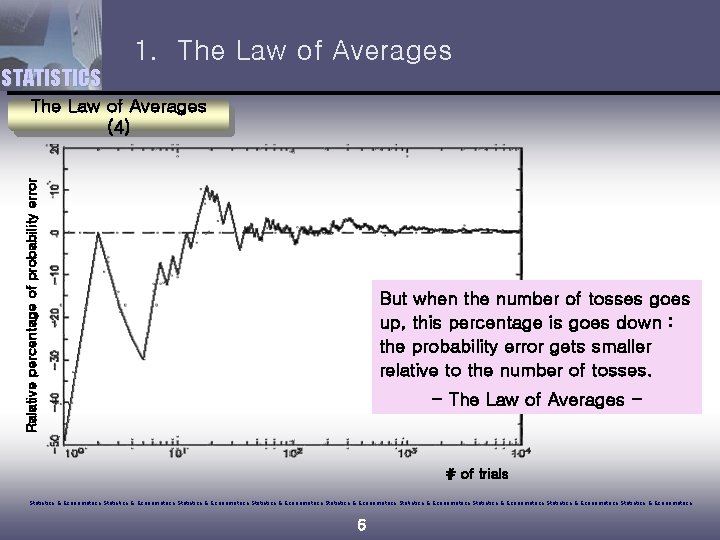
1. The Law of Averages STATISTICS Ralative percentage of probability error The Law of Averages (4) But when the number of tosses goes up, this percentage is goes down : the probability error gets smaller relative to the number of tosses. - The Law of Averages - # of trials Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 6

INDEX STATISTICS 1 The Law of Averages (Law of Large Numbers) 2 The Stochastic Processes 3 Making a Box Model Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 7

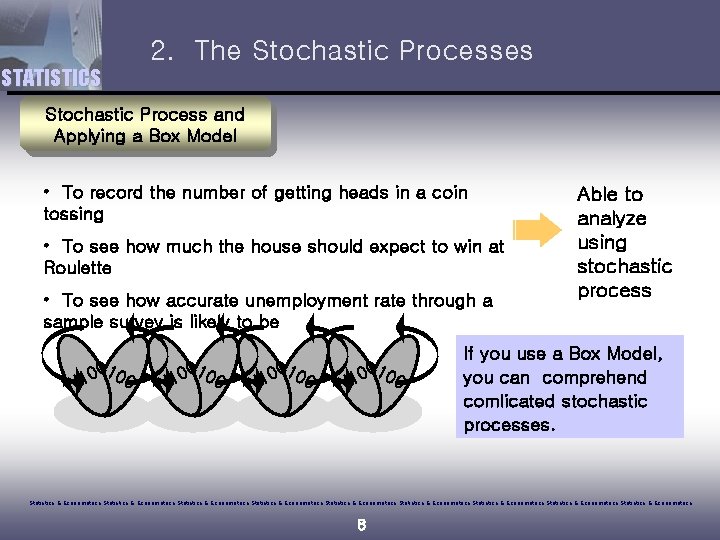
2. The Stochastic Processes STATISTICS Stochastic Process and Applying a Box Model • To record the number of getting heads in a coin tossing • To see how much the house should expect to win at Roulette • To see how accurate unemployment rate through a sample survey is likely to be 00100 1 Able to analyze using stochastic process If you use a Box Model, you can comprehend comlicated stochastic processes. Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 8

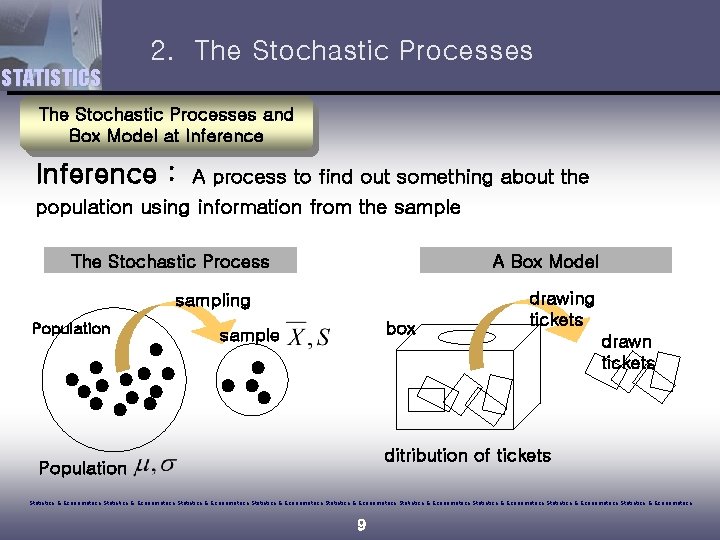
2. The Stochastic Processes STATISTICS The Stochastic Processes and Box Model at Inference : A process to find out something about the population using information from the sample The Stochastic Process A Box Model sampling Population box sample drawing tickets drawn tickets ditribution of tickets Population Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 9

INDEX STATISTICS 1 The Law of Averages (Law of Large Numbers) 2 The Stochastic Processes 3 Making a Box Model Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 10

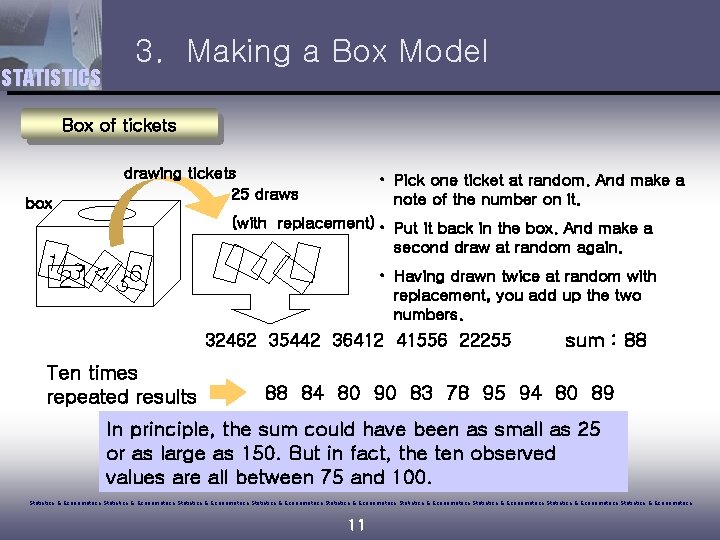
STATISTICS 3. Making a Box Model Box of tickets box drawing tickets 25 draws 13 4 6 2 5 • Pick one ticket at random. And make a note of the number on it. (with replacement) • Put it back in the box. And make a second draw at random again. • Having drawn twice at random with replacement, you add up the two numbers. 32462 35442 36412 41556 22255 Ten times repeated results sum : 88 88 84 80 90 83 78 95 94 80 89 In principle, the sum could have been as small as 25 or as large as 150. But in fact, the ten observed values are all between 75 and 100. Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 11

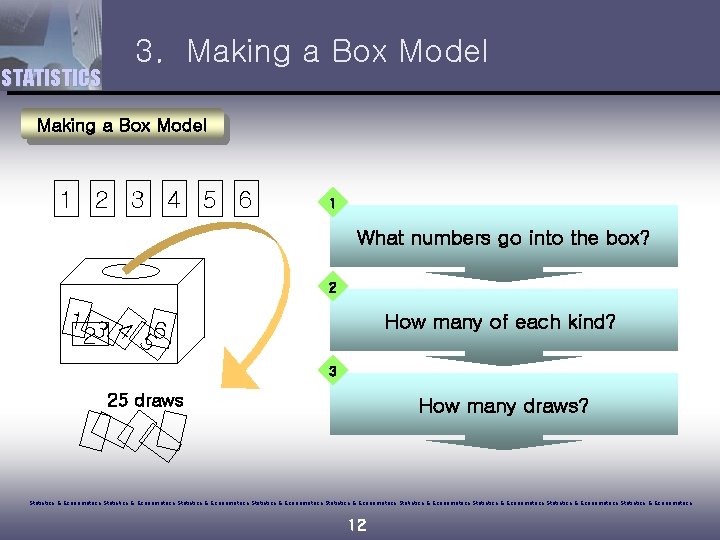
STATISTICS 3. Making a Box Model 1 2 3 4 5 6 1 What numbers go into the box? 2 13 4 6 2 5 How many of each kind? 3 25 draws How many draws? Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 12

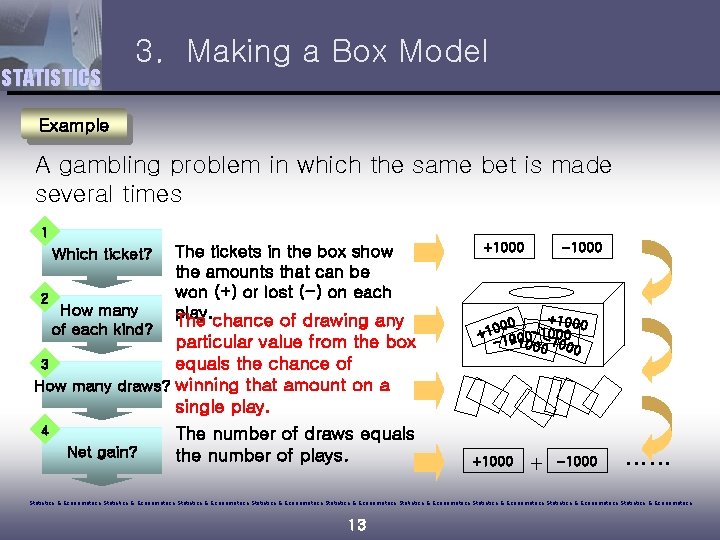
STATISTICS 3. Making a Box Model Example A gambling problem in which the same bet is made several times 1 Which ticket? 2 How many of each kind? The tickets in the box show the amounts that can be won (+) or lost (-) on each play. The chance of drawing any particular value from the box 3 equals the chance of How many draws? winning that amount on a single play. 4 The number of draws equals Net gain? the number of plays. +1000 -1000 +1000 0 +1 1+0100 -1 -0100 000 +1000 + -1000 …… Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 13