Statistics Econometrics Statistics Econometrics Statistics Econometrics Statistics for

Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics Statistics for Economist Ch. 10 The Binomial Formula 1. Sequence of Success and Fail 2. Bernoulli Random Variable 3. & Binomial Distribution 4. 3. The Binomial Formula Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics

INDEX STATISTICS 1 2 3 Sequence of Successes and Failures Bernoulli Random Variable & Binomial Distribution The Binomial Formula Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 2

1. Sequence of Successes & Failures STATISTICS Binomial Formula : application examples Ø When a coin is tossed 4 times, the probability of getting 1 head Ø When a die is rolled 10 times, the probability of getting 3 aces Ø The probability that the price of a stock which I bought today will increase for each 5 day Ø When 5 drawings are made at random with replacement draws from a box containing 1 red marbles and 9 green ones, the probability that 2 draws will be red When the outcome is divided into two parts (Success & Failure), the Probability is acquired by Binomial Formula Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 3

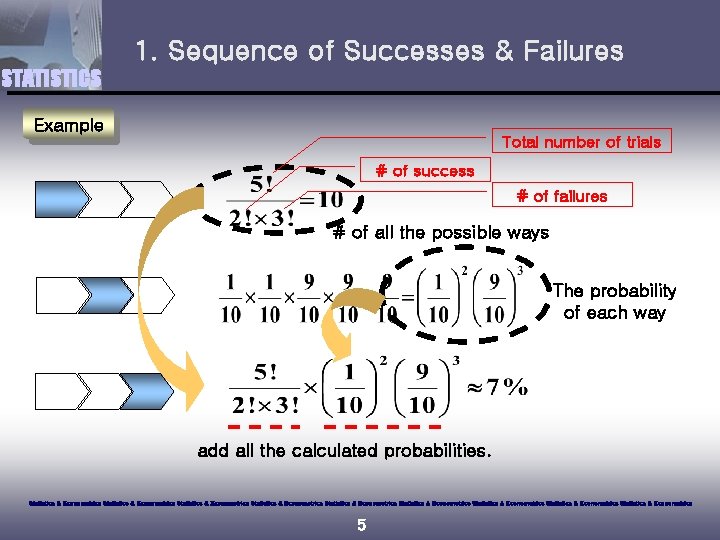
1. Sequence of Successes & Failures STATISTICS Example A Box contains 1 red marble and 9 green ones. Five draws are made at random with replacement. What is the probability that 2 draws will be red? ☞ the process of solution Find out all the possible ways Calculate the probability of each way Using Addition Rule, add all the calculated probabilities You can precede the second stage for convenience. Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 4

1. Sequence of Successes & Failures STATISTICS Example Total number of trials # of success # of failures # of all the possible ways The probability of each way add all the calculated probabilities. Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 5

INDEX STATISTICS 1 2 3 Sequence of Successes and Failures Bernoulli Random Variable & Binomial Distribution The Binomial Formula Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 6

STATISTICS 2. Bernoulli Random Variable & Binomial Distribution Bernoulli Random Variable ØBernoulli Trial § a trial in which the outcomes are divided into 2 parts Ø Bernoulli Random Variable § in a Bernoulli Trial, a random variable which assigns 1 to success and 0 to failure Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 7

STATISTICS 2. Bernoulli Random Variable & Binomial Distribution ØBernoulli Random Variable If we repeat identical Bernoulli trial n times independently, and let total number of successes be X , then X is denoted X = X 1 + X 2 + X 3 + … + Xn where X 1, X 2, … , Xn are random variables which assign 1 if the n-th outcome is success, and 0 to the failure ØIf the random variable X follows the binomial distribution, we write: X ~ B(n, p) Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 8

INDEX STATISTICS 1 2 3 Sequence of Successes and Failures Bernoulli Random Variable & Binomial Distribution The Binomial Formula Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 9

3. The Binomial Formula STATISTICS 이항공식 ØThe probability that success will occur k times out of n is given by the Binomial Formula n : # of trials, k : # of successes, p : probability of success ØThe Binomial Formula works under the following conditions § The value of n must be fixed in advance. § The trials must be independent. § p must be the same from trial to trial. Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 10

3. The Binomial Formula STATISTICS Example (1) EX 1) A die is rolled 10 times. What is the probability of getting 2 aces? ☞ EX 2) A die is rolled until it first lands six. If this can be done using the binomial formula, find the probability of getting 2 aces. If not, why not? ☞ n is not fixed in advance, the binomial formula does not apply. Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 11

3. The Binomial Formula STATISTICS 예 제 (2) EX 3) Ten draws are made at random with replacement from the box 1 1 2 3 4 5. However, just before the last draw is made, whatever has gone on, the ticket 5 is removed from the box. True or false : the probability of drawing two 1’s is ☞ False. Since the probability of getting 1 changes, the Binomial Formula does not apply. Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 12

3. The Binomial Formula STATISTICS Example (2) EX 4) Four draws are made at random without replacement from the box in exemple 3. True or false : the probability of drawing two 1’s is ☞ False. Trials are dependent, so the Binomial Formula does not apply. Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 13