Statistics Econometrics Statistics Econometrics Statistics Econometrics Statistics for

INDEX STATISTICS 1 Unit Transformation 2 The Normal Distribution Curve 3 Areas under the

STATISTICS 1. Unit Transformation Ø A transformation which adds a constant or multiply by

1. Unit Transformation STATISTICS Unit Transformation 1 2 3 4 5 6 7 Standardization

2. The Normal Distribution Curve STATISTICS Normal Distribution Curve Ø The normal distribution is

2. The Normal Distribution Curve STATISTICS Standard normal distribution ØAmong normal distributions, satisfying E(X)=0,

2. The Normal Distribution Curve STATISTICS A histogram for heights of women compared to

STATISTICS 3. Areas under the Normal Curve Finding areas under the normal curve (I)

3. Areas under the Normal Curve STATISTICS Finding areas under the normal curve(II) Ø

STATISTICS 4. Normal Approximation for Data The Average and SD Ø By the center

STATISTICS 4. Normal Approximation for Data Normal approximation Ex) What is the ratio of

5. Percentiles STATISTICS Histogram for families by income Ø Not all the histograms follow

STATISTICS 5. Percentiles for family income Ø Percentiles are good summaries for such a

6. Interquartile and box plot STATISTICS interquartile Ø interquartile the 25 th, 50 th

6. Interquartile and box plot STATISTICS Ø Five number summary for data: minimum, the

6. Interquartile and box plot STATISTICS Box plot (family income) Statistics & Econometrics Statistics

6. Interquartile and box plot STATISTICS Weekly profitability of firms in 2000 20 1

6. Interquartile and box plot STATISTICS Comparison of Samsung Electronics and POSCO 40 Weekly

7. Percentiles and Normal Curve STATISTICS Finding Percentiles Ø Ex) Estimate the score of

Slides: 25

Download presentation

Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics Statistics for Economist Chap 4. The Normal Approximation 1. 2. 3. 4. 5. 6. 7. Unit Transformation The Normal Distribution Curve Areas under the Normal Curve The Normal Approximation for Data Percentiles Interquartile and Box Plot Percentiles and the Normal Curve Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics

INDEX STATISTICS 1 Unit Transformation 2 The Normal Distribution Curve 3 Areas under the Normal Curve 4 The Normal Approximation for Data 5 Percentiles 6 Interquartile and Box Plot 7 Percentiles and the Normal Curve Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 2

STATISTICS 1. Unit Transformation Ø A transformation which adds a constant or multiply by a constant to a measurement value. Ø Standardization is a kind of unit transformation which subtracts average and divide by SD. Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 3

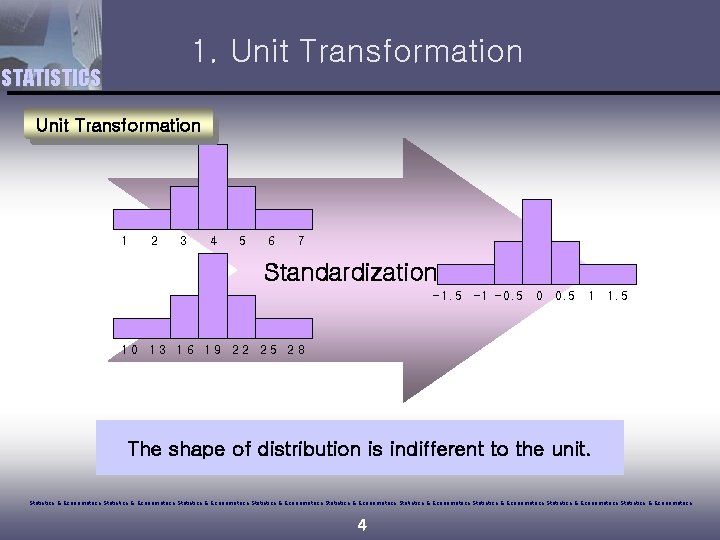
1. Unit Transformation STATISTICS Unit Transformation 1 2 3 4 5 6 7 Standardization -1. 5 – 1 – 0. 5 0 0. 5 1 1. 5 10 13 16 19 22 25 28 The shape of distribution is indifferent to the unit. Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 4

2. The Normal Distribution Curve STATISTICS Normal Distribution Curve Ø The normal distribution is an ideal histogram. This is a mathematical model approximating the distribution of the real data and is a distribution of population. m is population mean and is population standard deviation Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 6

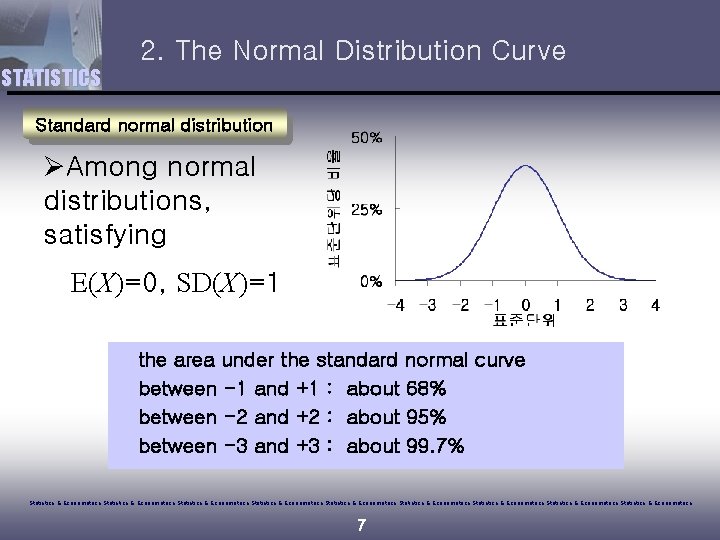
2. The Normal Distribution Curve STATISTICS Standard normal distribution ØAmong normal distributions, satisfying E(X)=0, SD(X)=1 the area under the standard normal curve between -1 and +1 : about 68% between -2 and +2 : about 95% between -3 and +3 : about 99. 7% Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 7

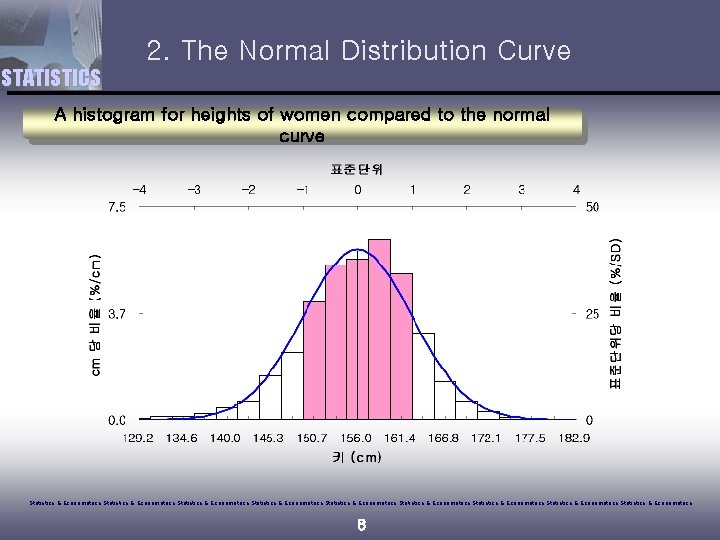
2. The Normal Distribution Curve STATISTICS A histogram for heights of women compared to the normal curve Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 8

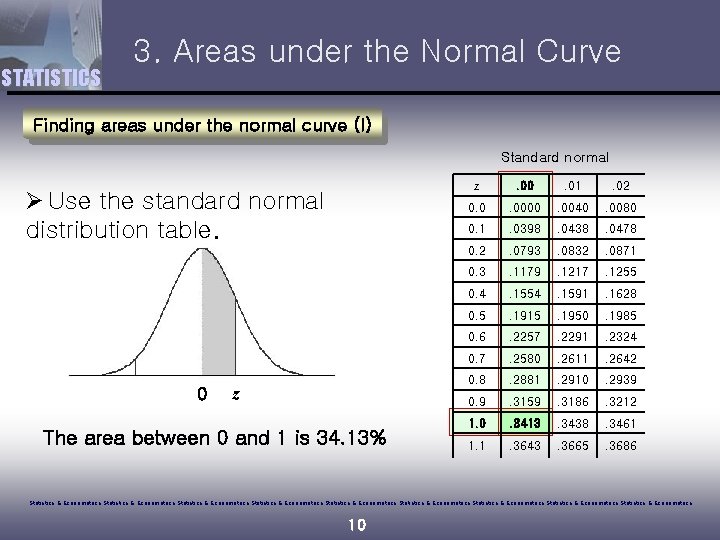
STATISTICS 3. Areas under the Normal Curve Finding areas under the normal curve (I) Standard normal Ø Use the standard normal distribution table. 0 z The area between 0 and 1 is 34. 13% z . 00 . 01 . 02 0. 0 . 0000 . 0040 . 0080 0. 1 . 0398 . 0438 . 0478 0. 2 . 0793 . 0832 . 0871 0. 3 . 1179 . 1217 . 1255 0. 4 . 1554 . 1591 . 1628 0. 5 . 1915 . 1950 . 1985 0. 6 . 2257 . 2291 . 2324 0. 7 . 2580 . 2611 . 2642 0. 8 . 2881 . 2910 . 2939 0. 9 . 3159 . 3186 . 3212 1. 0 . 3413 . 3438 . 3461 1. 1 . 3643 . 3665 . 3686 Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 10

3. Areas under the Normal Curve STATISTICS Finding areas under the normal curve(II) Ø Find the area between -2 and 1 under the standard normal distribution curve. = -2 1 + -2 0 0 1 ☞ the area between -2 and 0 is the same as the area between 0 and 2, by symmetry ☞ the area of it is about 48% and the area between 0 and 1 is about 34% ☞ so the area between -2 and 1 is about 48%+34%=82% Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 11

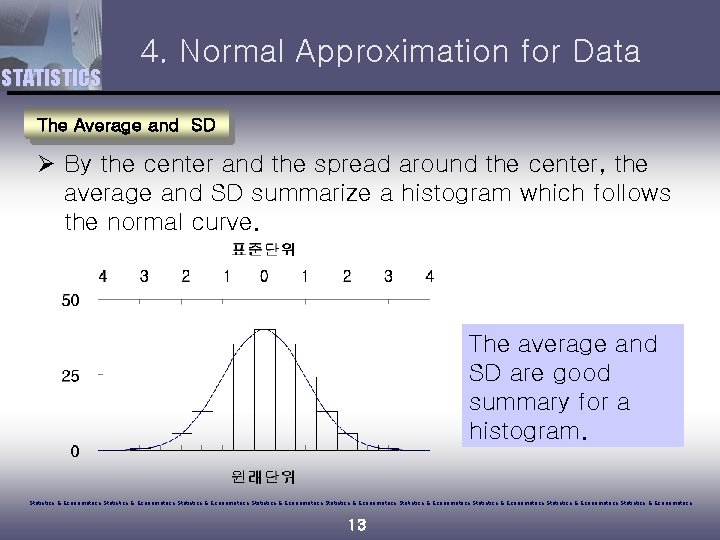
STATISTICS 4. Normal Approximation for Data The Average and SD Ø By the center and the spread around the center, the average and SD summarize a histogram which follows the normal curve. The average and SD are good summary for a histogram. Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 13

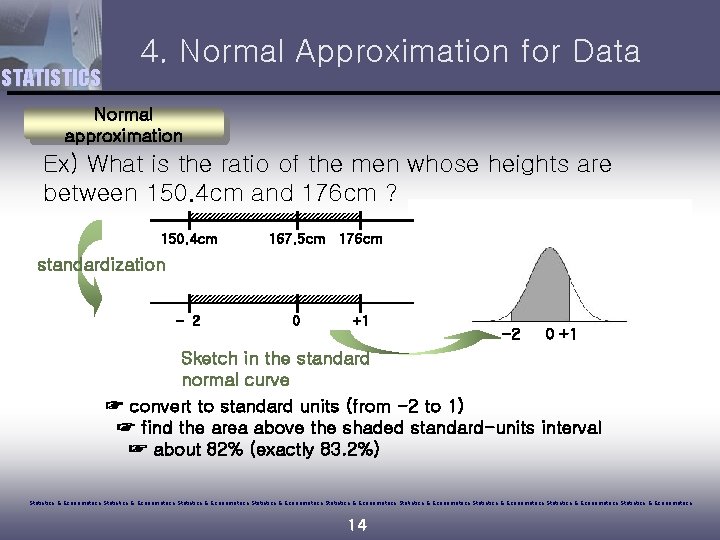
STATISTICS 4. Normal Approximation for Data Normal approximation Ex) What is the ratio of the men whose heights are between 150. 4 cm and 176 cm ? 150. 4 cm 167. 5 cm 176 cm standardization - 2 0 +1 -2 0 +1 Sketch in the standard normal curve ☞ convert to standard units (from -2 to 1) ☞ find the area above the shaded standard-units interval ☞ about 82% (exactly 83. 2%) Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 14

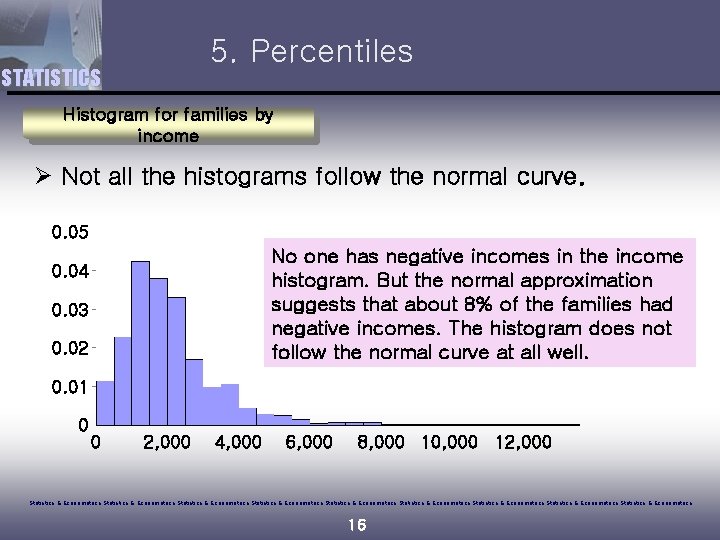
5. Percentiles STATISTICS Histogram for families by income Ø Not all the histograms follow the normal curve. 0. 05 No one has negative incomes in the income histogram. But the normal approximation suggests that about 8% of the families had negative incomes. The histogram does not follow the normal curve at all well. 0. 04 0. 03 0. 02 0. 01 0 0 2, 000 4, 000 6, 000 8, 000 10, 000 12, 000 Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 16

STATISTICS 5. Percentiles for family income Ø Percentiles are good summaries for such a histogram having a long tail. percentile income($10/year) 1 147. 3 10 743. 6 25 1, 200 50 1, 800 75 2, 572. 5 90 3, 696. 3 99 11, 540 10% of families had incomes of $7, 436 or less, and 90% were above. Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 17

6. Interquartile and box plot STATISTICS interquartile Ø interquartile the 25 th, 50 th and 75 th percentiles are the 1 st , 2 nd and 3 rd quartile. Especially, the 50 th percentile is just the median and the 2 nd quartile. Ø Interquartile Range (interquartile range)=(3 rd quartile)-(1 st quartile) Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 19

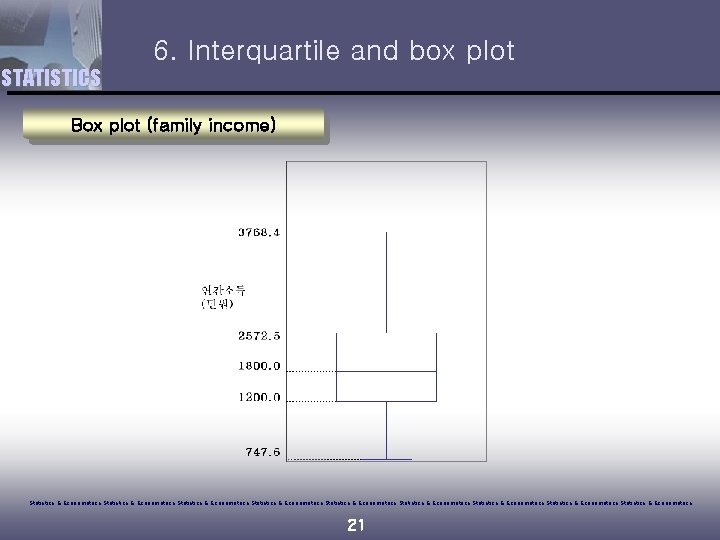
6. Interquartile and box plot STATISTICS Ø Five number summary for data: minimum, the 1 st quartile, 2 nd quartile, 3 rd quartile, and the maximum Ø Box plot describes the five number summary Ø Two vertical lines of the box indicates the minimum and the maximum. Ø Three horizontal lines in the box indicates three quartiles. Ø Sometimes the 10% and 90% are used instead. Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 20

6. Interquartile and box plot STATISTICS Box plot (family income) Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 21

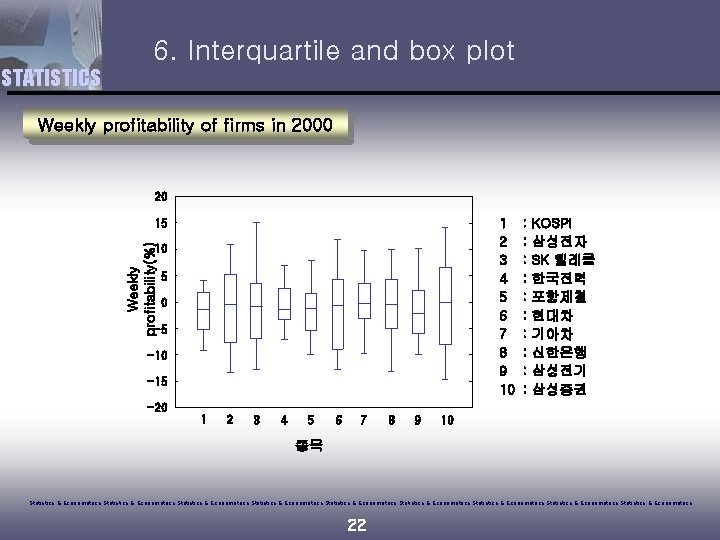
6. Interquartile and box plot STATISTICS Weekly profitability of firms in 2000 20 1 2 3 4 5 6 7 8 9 10 Weekly profitability(%) 15 10 5 0 -5 -10 -15 : : : : : KOSPI 삼성전자 SK 텔레콤 한국전력 포항제철 현대차 기아차 신한은행 삼성전기 삼성증권 -20 1 2 3 4 5 6 7 8 9 10 종목 Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 22

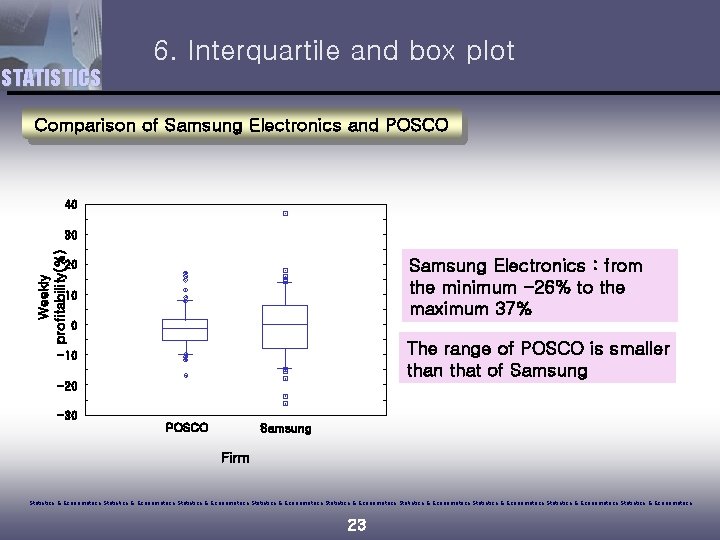
6. Interquartile and box plot STATISTICS Comparison of Samsung Electronics and POSCO 40 Weekly profitability(%) 30 Samsung Electronics : from the minimum -26% to the maximum 37% 20 10 0 The range of POSCO is smaller than that of Samsung -10 -20 -30 POSCO Samsung Firm Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 23

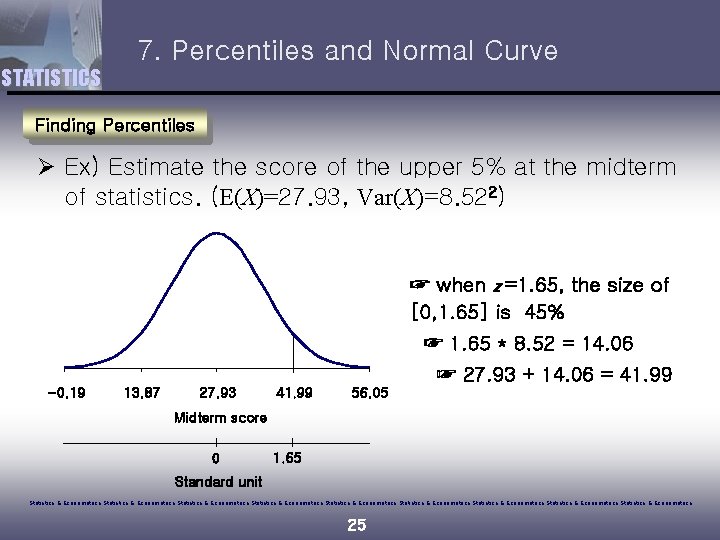
7. Percentiles and Normal Curve STATISTICS Finding Percentiles Ø Ex) Estimate the score of the upper 5% at the midterm of statistics. (E(X)=27. 93, Var(X)=8. 522) ☞ when z =1. 65, the size of [0, 1. 65] is 45% ☞ 1. 65 * 8. 52 = 14. 06 ☞ 27. 93 + 14. 06 = 41. 99 -0. 19 13. 87 27. 93 41. 99 56. 05 Midterm score 0 1. 65 Standard unit Statistics & Econometrics Statistics & Econometrics Statistics & Econometrics 25