Introduction to Econometrics 125 Econometrics Econometrics economic measurement























- Slides: 27

Introduction to Econometrics 1/25

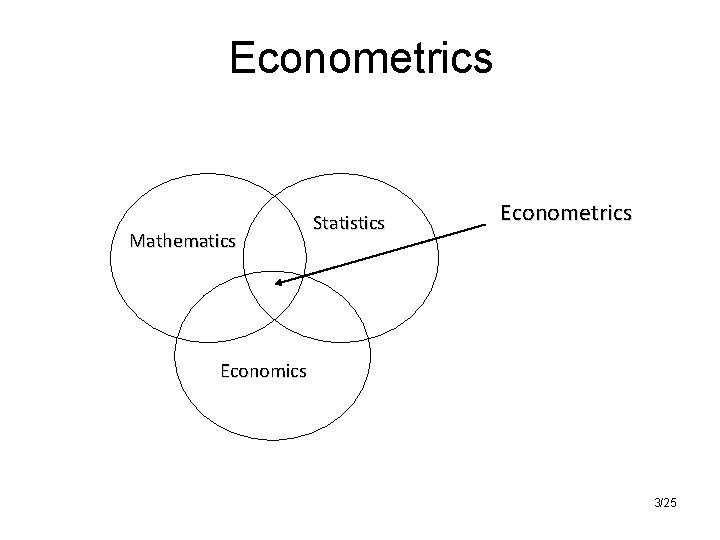
Econometrics • Econometrics – „economic measurement“ • „May be defined as the quantitative analysis of actual economic phenomena based on the concurrent development of theory and observation, related by appropriate methods of inference. “ (2 P. A. Samuelson, T. C. Koopmans, and J. R. N. Stone, “Report of the Evaluative Committee for Econometrica, ” Econometrica, vol. 22, no. 2, April 1954, pp. 141– 146. ) • Is an amalgam of economic theory, mathematical economics, economic statistics, and mathematical statistics. 2/25

Econometrics Mathematics Statistics Econometrics Economics 3/25

Methodology of Econometrics Traditional econometric methodology proceeds along the following lines: 1. Statement of theory or hypothesis 2. Specification of the mathematical model of theory 3. Specification of the statistical, or econometric model 4. Obtaining the data 5. Estimation of the parameters of the econometric model 6. Hypothesis testing 7. Forecasting or prediction 8. Using the model for control or policy purposes 4/25

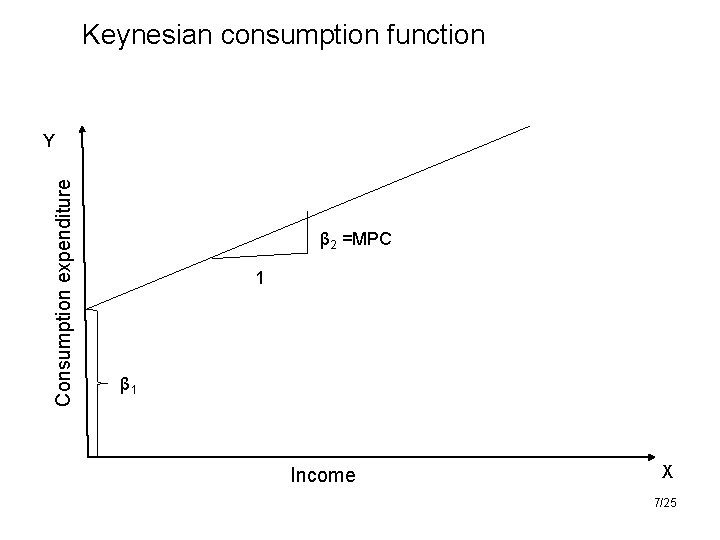
Example: 1. Statement of Theory or Hypothesis: Keynes stated: „The fundamental psychological law. . . Is that men (women) are disposed, as a rule and on average to increase their consumption as their income increases but not as much as the increase in their income. “ (John Maynard Keynes, The General Theory of Employment, Interest and Money, Harcourt Brace Jovanovich, New York, 1936, p. 96. ) • In short, Keynes postulated that the marginal propensity to consume (MPC), the rate of change of consumption for a unit (say, a dollar) change in income, is greater than zero but less than 1 5/25

2. Specification of the Mathematical Model of Consumption 6/25

Keynesian consumption function Consumption expenditure Y β 2 =MPC 1 β 1 Income X 7/25

• If the model has more than one equation, it is known as a multiple-equation model • If the model has only one equation, as in the preceding example, it is called a single-equation model • Variable appearing on the left side of the equality sign is called the dependent variable, and the variable(s) on the right side are called the independent or explanatory variable(s) 8/25

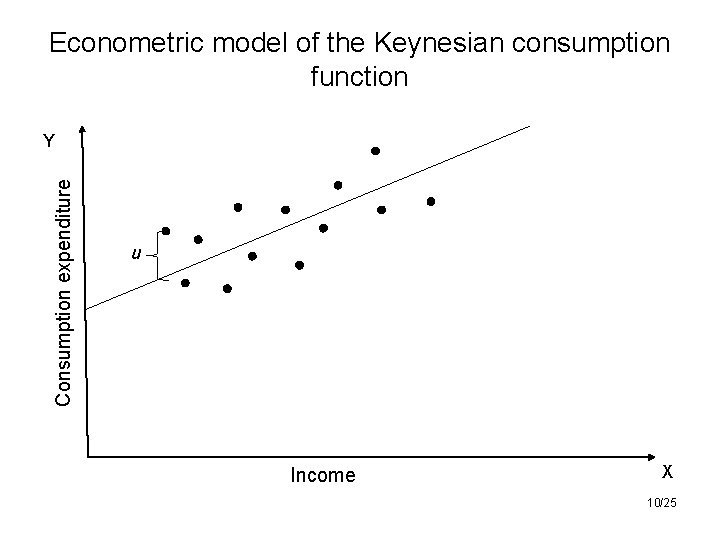
3. Specification of the Econometric Model of Consumption 9/25

Econometric model of the Keynesian consumption function Consumption expenditure Y u Income X 10/25

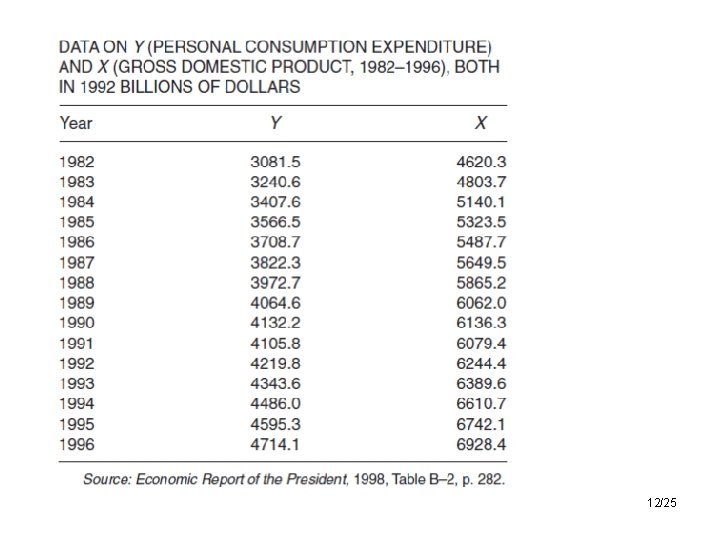
4. Obtaining Data • To estimate the econometric model, that is, to obtain the numerical values of β 1 and β 2, we need data • Three types of data may be available for empirical analysis: time series (data collected over a period of time), cross-sectional data (data collected at one point in time) and pooled (combination of time series and cross-section) 11/25

12/25

5. Estimation of the Econometric Model equal to 0 13/25

6. Verification of the model and hypothesis testing • Economic verification – we have to find out if the estimates obtained are in accord with the expectations of theory that is being tested • Statistical verification – significance of the model and significance of the coefficients • Econometric verification – if the estimated model meet the assumptions of the classical linear regression model 14/25

Economic verification • As noted earlier, Keynes expected the MPC to be positive but less than 1. • In our example we found the MPC to be about 0, 7 • But before we accept this finding as confirmation of Keynesian consumption theory, we must enquire whether this estimate is sufficiently below unity to convince us that this is not a chance occurrence or peculiarity of the particular data we have used -> is 0, 7 statistically less than 1? • =>Statistical inference 15/25

Statistical verification 16/25

Statistical verification 17/25

R 2: A measure of goodness of fit of the estimated regression 18/25

Econometric verification • Assumptions of classical linear regression model (CLRM) • The regression model is linear in parameters. It may or may not be linear in the variables Y and the Xs. • X values are fixed in repeated sampling. Values taken by the regressor X are considered fixed in repeated samples. More technically, X is assumed to be non-stochastic. • Zero mean value of disturbance ui. Given the value of X, the mean, or expected , value of the random disturbance term ui is zero. Technically, the conditional mean value of ui is zero. • The variance of each ui, given the values of X, is constant, or homoscedastic. • There is no correlation between two error terms. That is, there is no autocorrelation. • Zero covariance between ui and Xi 19/25

Econometric verification • The number of observations n must be greater than the number of parameters to be estimated • The X values in a given sample must not all be the same. Technically, var(X) must be a finite positive number. • The regression model is correctly specified. Alternatively, there is no specification bias or error in the model used in empirical analysis • There is no perfect multicollinearity, that is there are no perfect linear relationships among the explanatory variables. • Error term follows the normal distribution with zero mean and constant variance 20/25

7. Forecasting or prediction 21/25

2: Dummy variables (variables with only two values, zero and one) 22/25

Dummy variables • Such variables are a device to classify data into mutually exclusive categories such as male or female • If a qualitative variable has m categories, introduce only (m 1) dummy variable, thus, for each qualitative regressor the number of dummy variables introduced must be one less than the categories of the variable • If you do not follow this rule, you will fall into what is called the dummy variable trap – situation of perfect collinearity • The category for which no dummy variable is assigned is known as the base, benchmark, reference, or omitted category, and all comparisons are made in relation to the benchmark category • The coefficients attached to the dummy variables are known as the differrential intercept coefficients because they tell by how much the value of the intercept that receives the value of 1 differs from the intercept coefficient of the benchmark category. 23/25

Example: PUBLIC SCHOOL TEACHERS’ SALARIES BY GEOGRAPHICAL REGION •

• 25/25

Example: TEACHER’S SALARY IN RELATION TO REGION AND SPENDING ON PUBLIC SCHOOL PER PUPIL •

27/25