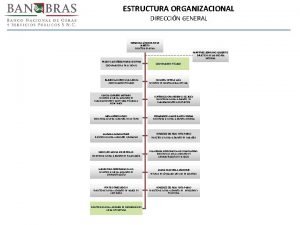
Sistemas Inteligentes verano 2011 Dr P Jorge Escamilla

Sistemas Inteligentes verano 2011 Dr. P. Jorge Escamilla Ambrosio jescami@inaoep. mx, pjorgeea@gmail. com, http: //elca 1. inaoep. mx/~jescami/

Sistemas Inteligentes Temario ¢ Lógica difusa l Introducción l Conjuntos difusos • Operaciones conjuntos difusos l Sistemas de inferencias difusos (SID) • Fuzzificación • Evaluación de reglas • Defuzzificación l l Tipos de SID Aplicaciones de SID • • • Histograma “suave” (soft histogram) Memoria asociativa Control difuso tipo PID Fuzzy Adaptive Kalman Filter Extracción de características y clasificación

Sistemas Inteligentes Temario ¢ Redes Neuronales Artificiales (RNA) l l Introducción Principal idea y terminología • • • l Principales tipos de RNA • • • l Perceptron Backpropagation Radial basis function RNA Aplicaciones de RNA • • ¢ Fundamentos biológicos Clasificación de RNA Funciones de activación Identificación Control Sistemas Neuro-Difusos (Neuro-fuzzy) l l Diferentes combinaciones Equivalencia entre SID y RNA ANFIS Aplicaciones • • Identificación Neurofuzzy-AKF

Sistemas Inteligentes Bibliografía ¢ ¢ ¢ Haykin, S. (1994). Neural Networks A Comprehensive Foundation. Macmillan College Publishing Company, Inc. , NY. Brown, M. and Harris, C. (1994). Neurofuzzy Adaptive Modelling and Control, Prentice Hall International (UK) Limited. Jang, J. -S. R. , Sun, C. -T. and Mizutani, E. (1996). Neuro-Fuzzy Soft Computing: A Computational Approach to Learning and Machine Intelligence, Prentice Hall. Pedrycz, W, and Gomide, F. (2007). Fuzzy Systems Engineering Towards Human-Centric Computing, IEEE Press. Driankov, D. , Hellendoorn, H. , and Reinfrank, M. (1993). An Introduction to Fuzzy Control, Springer-Verlag. Paplinski, A. P. (2005). CSE 5301 Neural Networks and Fuzzy Systems (Neuro-Fuzzy Computing), Lecture notes, Monash University. http: //www. csse. monash. edu. au/courseware/cse 5301/2006/

Sistemas Inteligentes Evaluación 2 examen parciales (40%) ¢ 2 series (20%) ¢ 1 proyecto final (40%) ¢

Lógica difusa (borrosa) Introducción ¢ ¢ ¢ La imprecisión y la incertidumbre son conceptos inherentes a la naturaleza inexacta del razonamiento humano Nuestra manera de interpretar el mundo generalmente es en función de proposiciones vagas, datos inciertos y juicios de valor Esta imprecisión e incertidumbre no son tomadas en cuenta por la lógica tradicional (crisp logic) en donde sólo existen dos premisas fundamentales: verdadero y falso

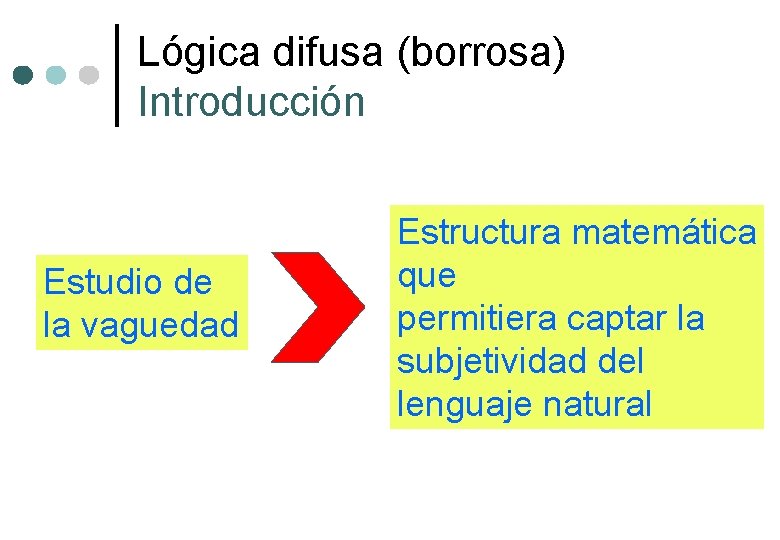
Lógica difusa (borrosa) Introducción Estudio de la vaguedad Estructura matemática que permitiera captar la subjetividad del lenguaje natural

Lógica difusa (borrosa) Introducción Charles Sanders Pierce (1839 -1914) • Todo cuanto existe es continuo y, por tanto, tal continuidad gobierna el conocimiento “La vaguedad no se puede descartar del mundo de la lógica así como la fricción de la mecánica” Bertrand Rusell (1872 -1970) • Ambas, vaguedad y precisión son características del lenguaje no de la realidad • La vaguedad claramente es materia de gradación

Lógica difusa (borrosa) Introducción Jan Lukasiewicz (1878 -1956) • Da los pasos necesarios para formalizar un modelo de la vaguedad • Lógica de tres valores: 1 – cierto, 0 – falso y ½ posible Max Black (1909 -1988) • Sugirió que los términos vagos podían formar conjuntos ("conjuntos vagos") • Un conjunto podía ser un subconjunto parcial de otro Albert Einstein (1879 -1955) “Tan pronto como las leyes de las matemáticas se refieren a la realidad, estas no son ciertas y tan pronto como estas leyes son ciertas, estas no se refieren a la realidad”

Lógica difusa (borrosa) Introducción Lotfi Zadeh (1923 - ) • En 1965 publicó "Fuzzy Sets" (conjuntos difusos) “En la medida en que la conplejidad de un sistema se incrementa, nuestra habilidad para hacer juicios precisos y significativos hacerca de su comportamiento disminuye hasta que un limite se alcanza, mas alla del cual precisión y significativo se vuelven conceptos mutuamente exclusivos” • Entre mas cerca se analiza un problema real, mas difuso se vuelve su solución

Lógica difusa (borrosa) Introducción “El fundamento teórico de la lógica difusa es, de hecho, preciso y netamente matemático. Entonces, la fuente de impresición en la teoría de la lógica difusa no es su entendimiento (fundamentación), sino la manera en que ésta se aplica para solucionar problemas del mundo real”

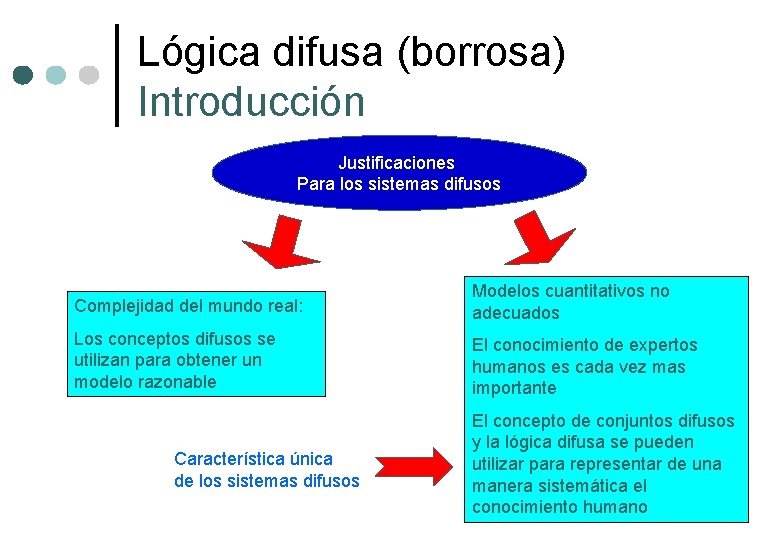
Lógica difusa (borrosa) Introducción Justificaciones Para los sistemas difusos Complejidad del mundo real: Modelos cuantitativos no adecuados Los conceptos difusos se utilizan para obtener un modelo razonable El conocimiento de expertos humanos es cada vez mas importante Característica única de los sistemas difusos El concepto de conjuntos difusos y la lógica difusa se pueden utilizar para representar de una manera sistemática el conocimiento humano

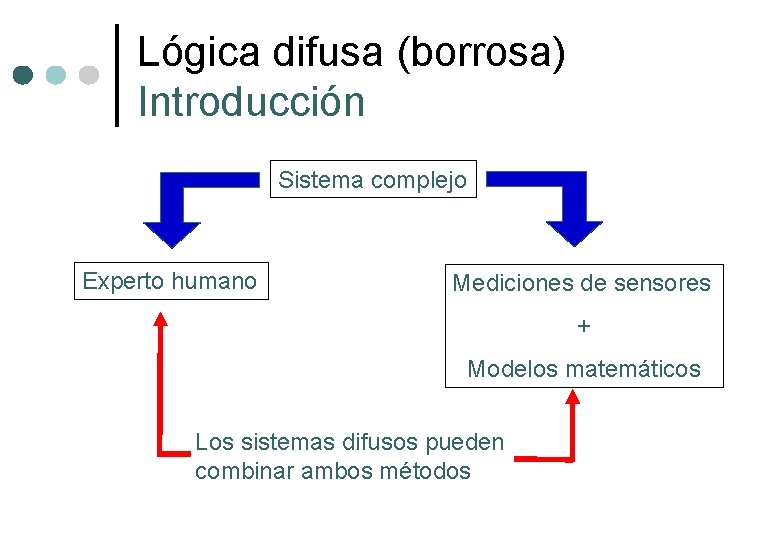
Lógica difusa (borrosa) Introducción Sistema complejo Experto humano Mediciones de sensores + Modelos matemáticos Los sistemas difusos pueden combinar ambos métodos

Lógica difusa (borrosa) Introducción Aplicaciones de sistemas difusos Control Comunicaciones Procesamiento de señales Sistemas expertos Diseño y fabricación de circuitos integrados Medicina Psicología

Lógica difusa (borrosa) Introducción ¢ Desarrollo de la tecnología difusa l l l l l 1965 Concepto de los conjuntos difusos por Lotfi Zadeh (USA) 1972 Primer grupo de trabajo en sistemas difusos en Japón liderados por Toshiro Terano 1973 Publicacion sobre algoritmos difusos por Zadeh (USA) 1977 Primer sistema experto difuso para evaluar aplicaciones para prestamos por Hans Zimmermann (Alemania) 1980 Control de horno para fabricar cemento por F. -L. Smidth & Co. – Lauritz P. Holmblad (Dinamarca). Primera aplicacion industrial. 1980 Sistema difuso para ajedrez y backgammon –Hans Berliner (USA) 1984 Sistema de control para el tratamiento de agua (inyección química) (Japón) 1984 Sistema de control para el metro de Sandai (Japón) 1985 Primer chip difuso desarrollado por Masaki Togai y Hiroyuke Watanabe en Bell Labs (USA) 1986 Sistema experto difuso para el diagnóstico de enfermedades desarrollado en Omron (Japón)

Lógica difusa (borrosa) Introducción ¢ Desarrollo de la tecnología difusa l l l l 1987 Control de grúa para contenedores 1987 Control para excavación de túneles 1987 Robot soldador 1987 Control automático para aterrizaje de aviones 1987 Segunda conferencia IFSA en Tokio 1987 Fundación de Togai Infra. Logic Inc. – primera compania desarrolladora de sistemas difusos en Irvine (USA) 1988 Control de horno desarrollado por Yokogawa 1988 Primer controlador dedicado vendido por Omron (Japón) 1989 Creación de “Laboratory for International Fuzzy Engineering Research (LIFE)” en Japón 1990 Televisión difusa desarrollada por Sony (Japón) 1990 Ojo electronico difuso desarrollado por Fujitsu (Japón) 1990 Fundación de “Fuzzy Logic Systems Institute (FLSA)” por Takeshi Yamakawa (Japón) 1990 Fundación del “Intelligent Systems Control Laboratory” en Siemens (Alemania) 1991 Centro de promoción de AI difusa (Japón) 1991 Kit educacional sobre sistemas difusos por Motorola (USA) 1992 A partir de aqui, son demasiado los desarrollos, invenciones y proyectos para ser mencionados.

Lógica difusa ¢ Universo del discurso X ¢ Es una colección de objetos denotados genéricamente como {x} y pueden ser discretos o continuos Conjunto difuso A El conjunto difuso A en X esta caracterizado por una función de membresía que asocia a cada elemento x en X un número en el intervalo [0, 1]

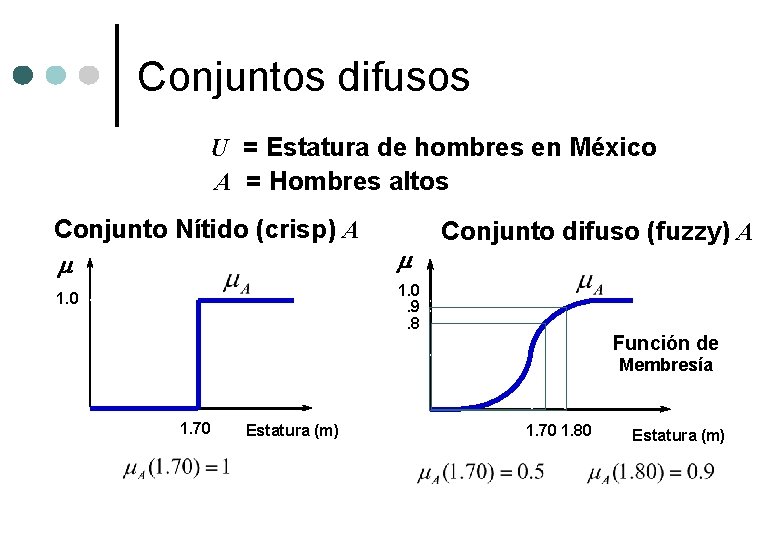
Conjuntos difusos U = Estatura de hombres en México A = Hombres altos Conjunto Nítido (crisp) A Conjunto difuso (fuzzy) A 1. 0. 9. 8 1. 0 Función de Membresía 1. 70’’ Estatura (m) 1. 70 1. 80 Estatura (m)

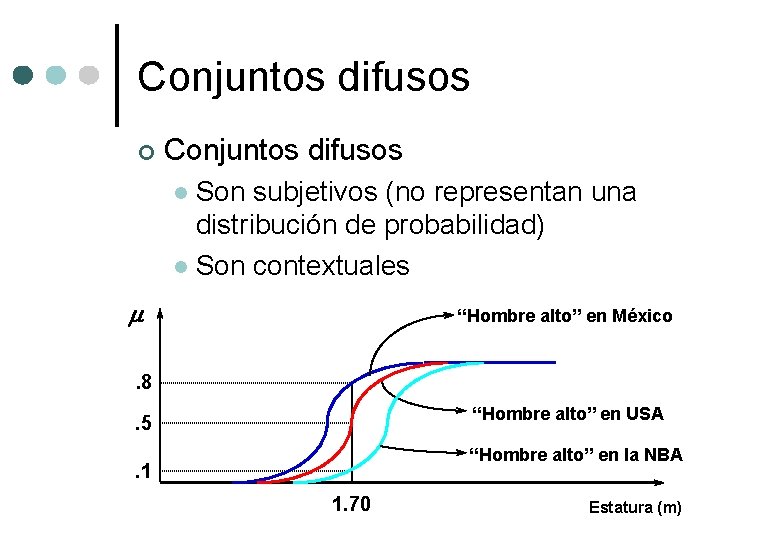
Conjuntos difusos ¢ Conjuntos difusos Son subjetivos (no representan una distribución de probabilidad) l Son contextuales l “Hombre alto” en México . 8 “Hombre alto” en USA . 5 “Hombre alto” en la NBA . 1 1. 70 Estatura (m)

Conjuntos difusos ¢ Representación formal de un conjunto difuso Un conjunto difuso A en X se expresa como el conjunto de pares ordenados del elemento genérico x y su respectivo grado de membresía: Conjunto Difuso Grado de Membresía Universo del Discurso Un conjunto difuso esta totalmente caracterizado por su función de membresía

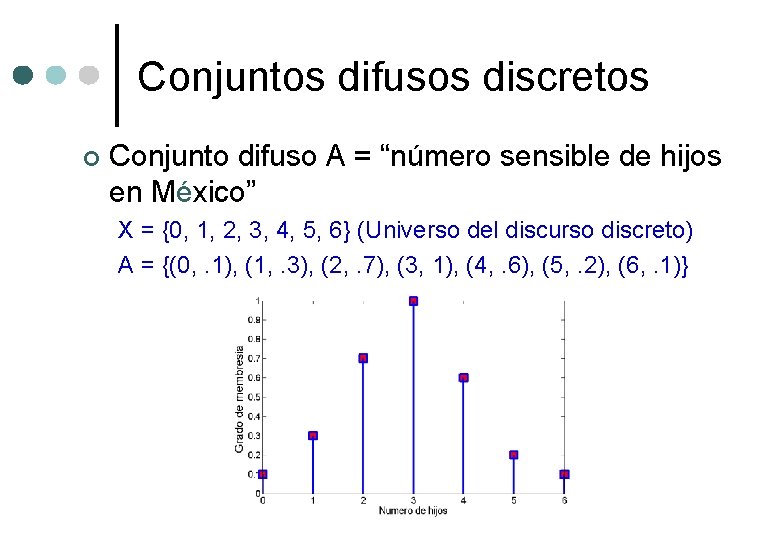
Conjuntos difusos discretos ¢ Conjunto difuso A = “número sensible de hijos en México” X = {0, 1, 2, 3, 4, 5, 6} (Universo del discurso discreto) A = {(0, . 1), (1, . 3), (2, . 7), (3, 1), (4, . 6), (5, . 2), (6, . 1)}

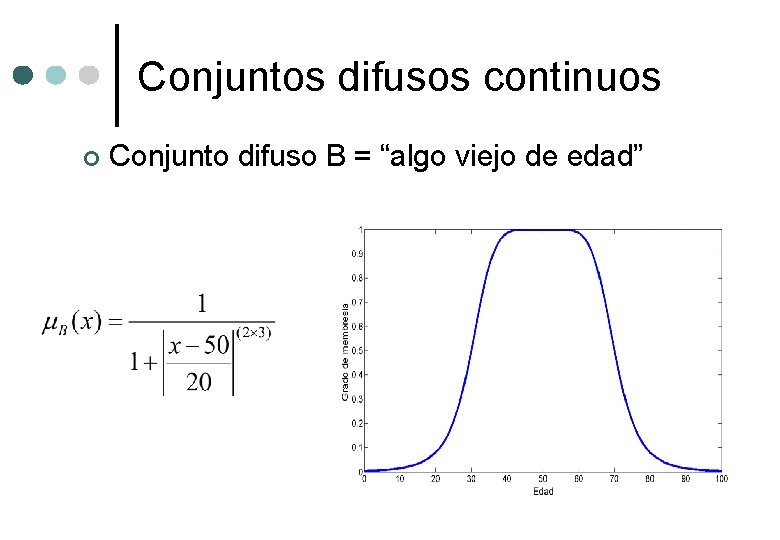
Conjuntos difusos continuos ¢ Conjunto difuso B = “algo viejo de edad”

Conjuntos difusos ¢ Representación alternativa X es discreto X es continuo Notar que los símbolos S y representan unión de grados de membresía; el simbolo “/” se utiliza como un marcador no implicando división numérica.

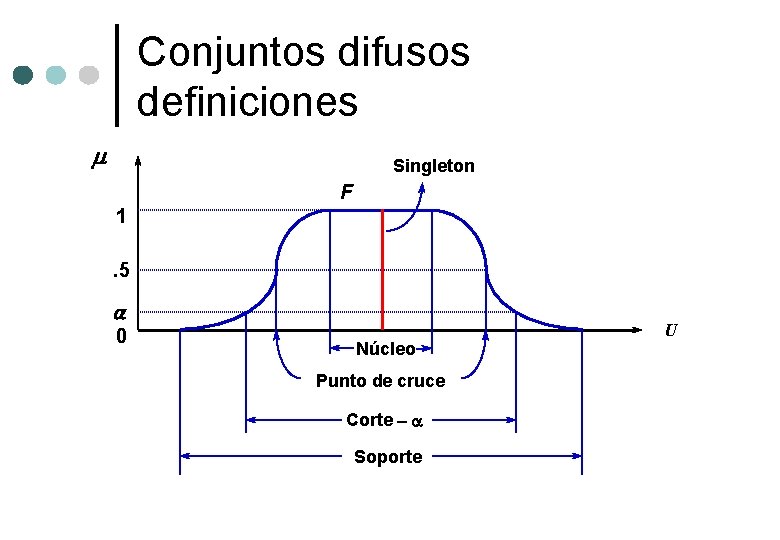
Conjuntos difusos definiciones ¢ Soporte l ¢ El soporte Supp(F) del conjunto difuso F es el conjunto nítido (no difuso) de todos los puntos u de U tales que F(u)>0 Punto de cruce l Es el elemento u en U para el que F(u)=0. 5

Conjuntos difusos definiciones ¢ Singleton l ¢ Es un conjunto difuso F cuyo soporte es un único punto en U con F(u)=1. 0 Conjunto difuso compacto l El conjunto difuso F se dice que es compacto si su soporte es finito

Conjuntos difusos definiciones ¢ Conjunto corte- l ¢ Es el conjunto nítido de los elementos que pertenecen al conjunto difuso F en al menos el grado : Conjunto corte- firme

Conjuntos difusos definiciones ¢ Ancho de un conjunto difuso l El ancho width de un conjunto difuso convexo F con soporte Supp(F) esta definido por: l Donde sup e inf denotan las operaciones matemáticas de supremo y el ínfimo, respectivamente:

Conjuntos difusos definiciones ¢ Núcleo l El núcleo (core) de un conjunto difuso F es el conjunto nítido que contiene todos los valores con grado de membresía igual a 1: núcleo(F) ={u U / F(u) = 1} ¢ Valor pico l Si solamente existe en U un punto con grado de membresía en F igual a 1, entonces este punto es el valor pico

Conjuntos difusos definiciones ¢ Altura de un conjunto difuso l La altura de un conjunto difuso F, hgt(F), esta dada por el grado de membresía supremo sobre toda u en U: l F es normal si hgt(F) = 1 y es subnormal si hgt(F) < 1

Conjuntos difusos definiciones Singleton F 1. 5 a 0 Núcleo Punto de cruce Corte - a Soporte U

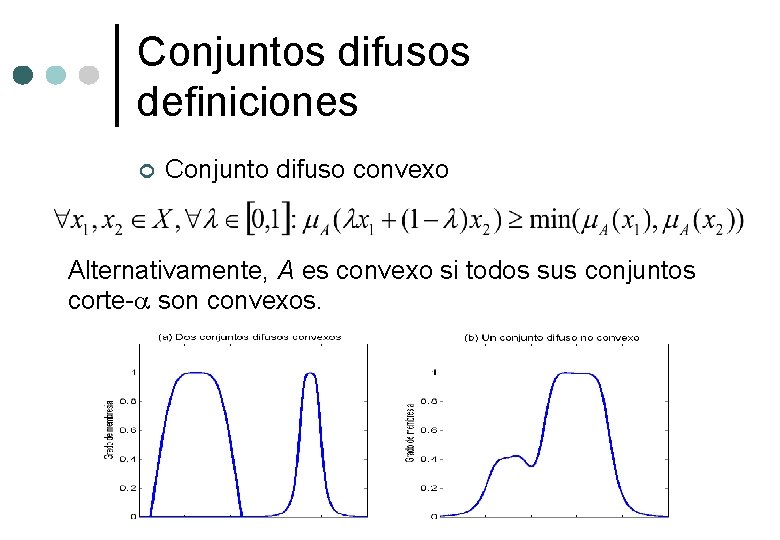
Conjuntos difusos definiciones ¢ Conjunto difuso convexo Alternativamente, A es convexo si todos sus conjuntos corte-a son convexos.

Conjuntos difusos definiciones ¢ Número difuso l Un número difuso F en el universo de discurso continuo U, es un conjunto difuso que es normal y convexo. ¢ Cardinalidad de un conjunto difuso: ¢ Cardinalidad relativa:

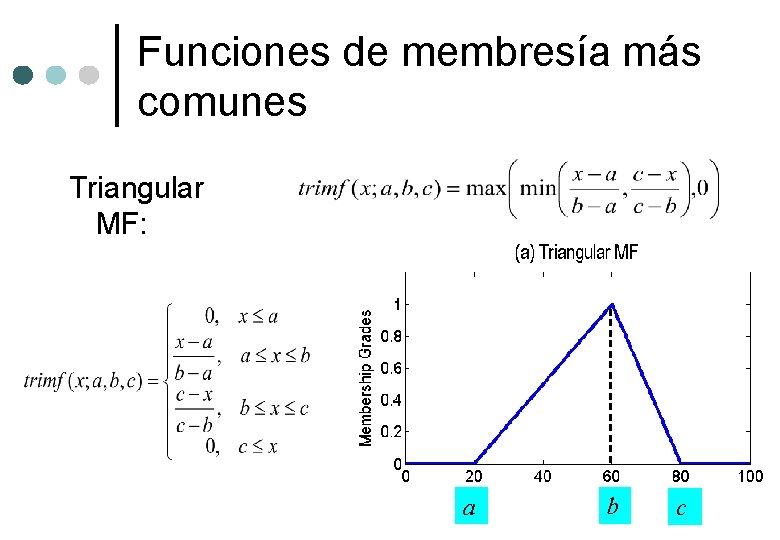
Funciones de membresía más comunes Triangular MF: a b c

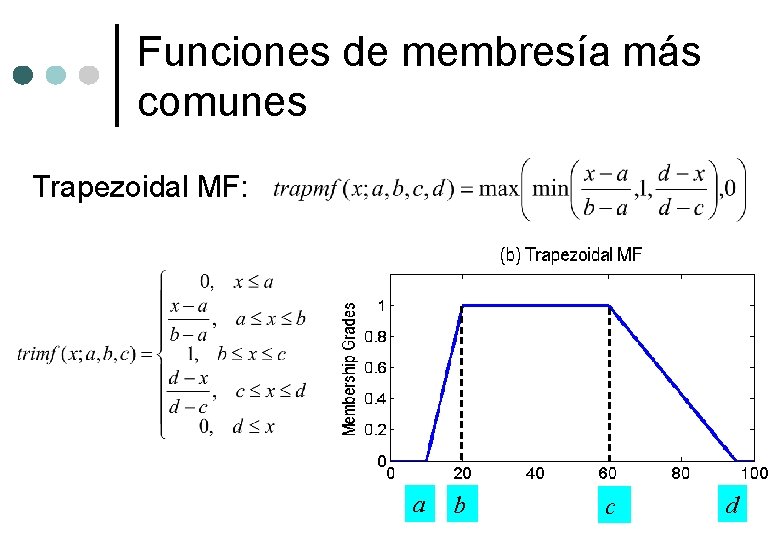
Funciones de membresía más comunes Trapezoidal MF: a b c d

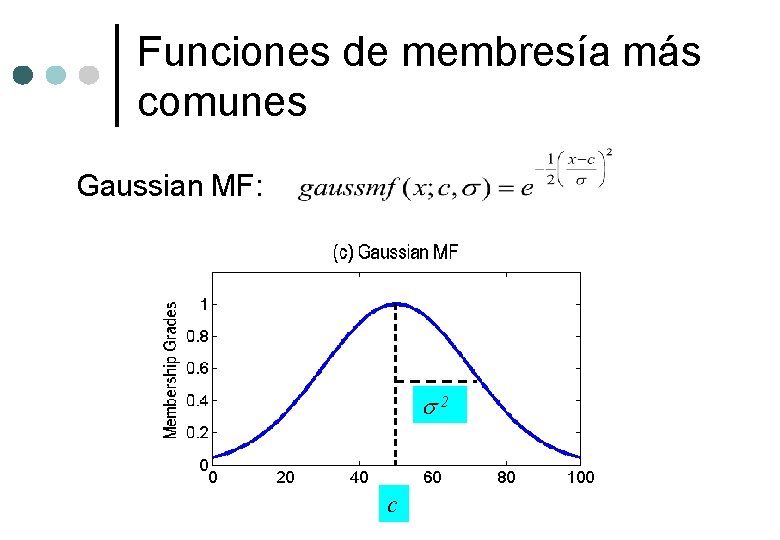
Funciones de membresía más comunes Gaussian MF: 2 c

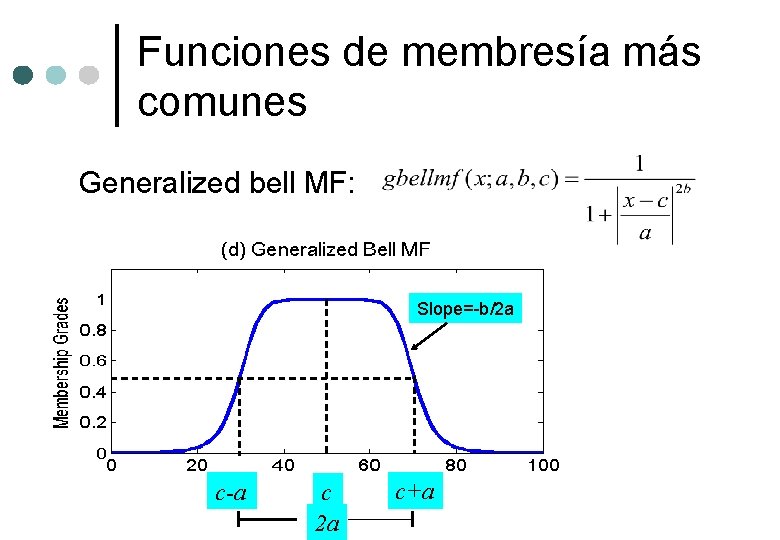
Funciones de membresía más comunes Generalized bell MF: Slope=-b/2 a c-a c 2 a c+a

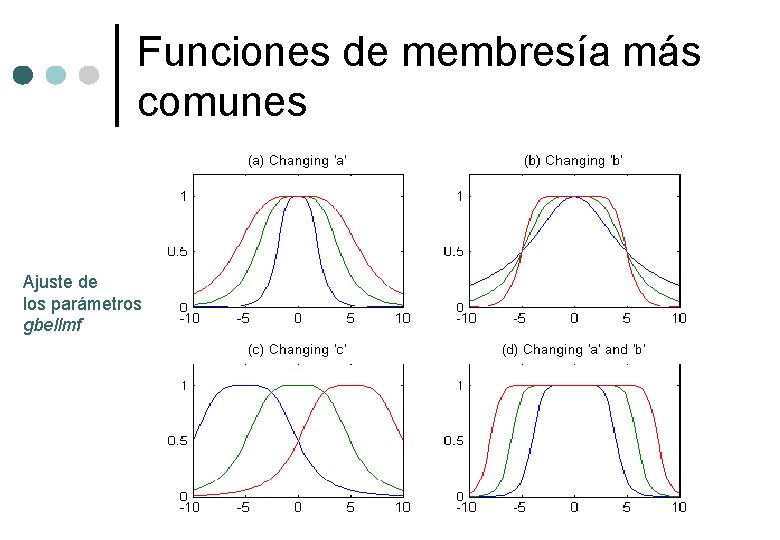
Funciones de membresía más comunes Ajuste de los parámetros gbellmf

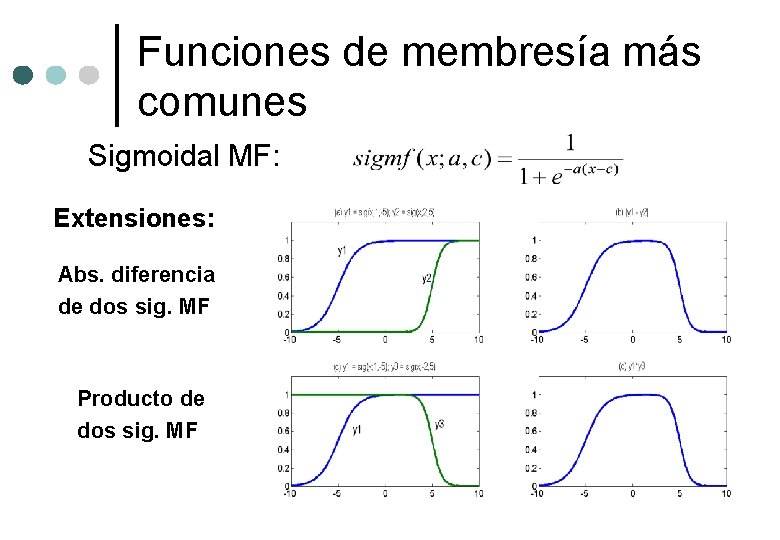
Funciones de membresía más comunes Sigmoidal MF: Extensiones: Abs. diferencia de dos sig. MF Producto de dos sig. MF

Operaciones básicas conjuntos difusos ¢ Conjunto vació: Un conjunto difuso esta vacío si y sólo si A(U)=0 l y es universal si y sólo si l ¢ Igualdad l Dos conjuntos difusos A y B son iguales (A=B) si y sólo si

Operaciones básicas conjuntos difusos ¢ Subconjunto: ¢ Complemento: ¢ Unión: ¢ Intersección:

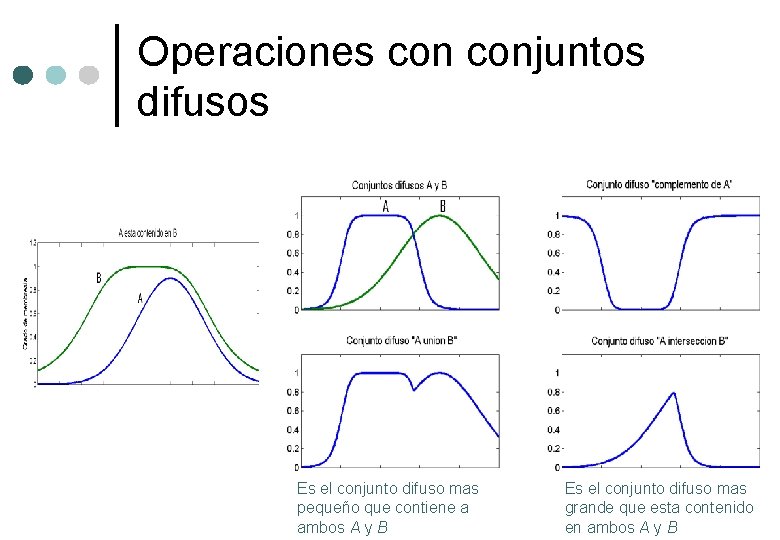
Operaciones conjuntos difusos Es el conjunto difuso mas pequeño que contiene a ambos A y B Es el conjunto difuso mas grande que esta contenido en ambos A y B

T-norma (Norma triangular) ¢ ¢ Requerimientos básicos: l Acotado: T(0, 0) = 0, T(a, 1) = T(1, a) = a l Monotonicidad: T(a, b) < T(c, d) si a < c y b < d l Conmutatividad: T(a, b) = T(b, a) l Asociatividad: T(a, T(b, c)) = T(T(a, b), c) Ejemplos: Mínimo: Producto algebraico: Lukasiewicz: Degenerada:

T-conorma o S-norma ¢ ¢ Requerimientos básicos: l Acotado: S(1, 1) = 1, S(a, 0) = S(0, a) = a l Monotonicidad: S(a, b) < S(c, d) if a < c and b < d l Conmutativididad: S(a, b) = S(b, a) l Asociatividad: S(a, S(b, c)) = S(S(a, b), c) Ejemplos: Maximo: Suma probabilística: Lukasiewicz: Degenerada:

Producto Cartesiano ¢ ¢ ¢ Dados conjuntos difusos A U y B V, el producto cartesiano de A y B denotado como A B se define por U V es la coleccion de pares ordenados (u, v) tales que De manera general: T = min T = producto algebraico

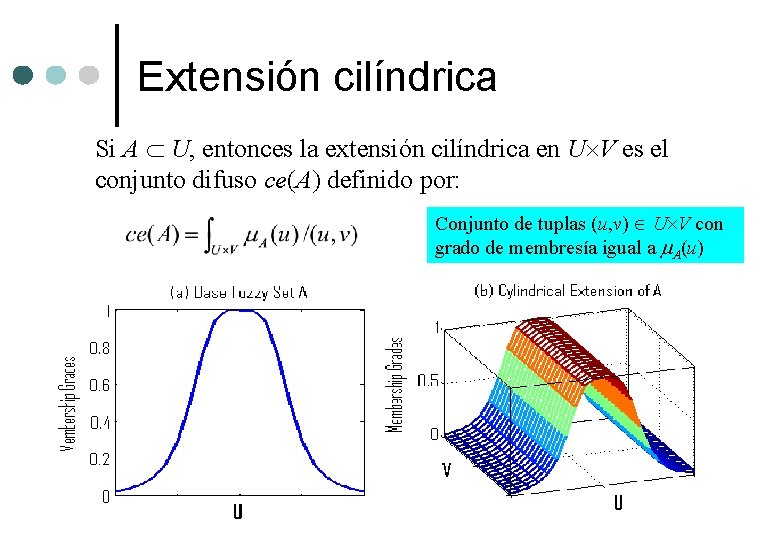
Extensión cilíndrica Si A U, entonces la extensión cilíndrica en U V es el conjunto difuso ce(A) definido por: Conjunto de tuplas (u, v) U V con grado de membresía igual a A(u)

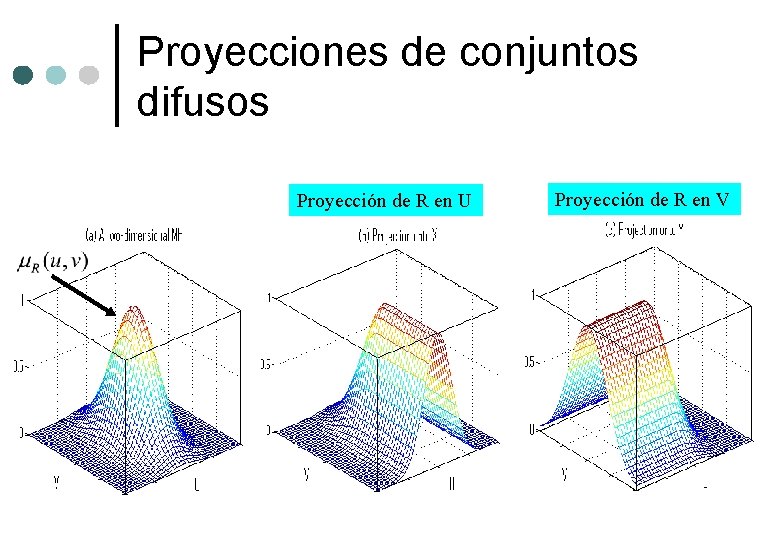
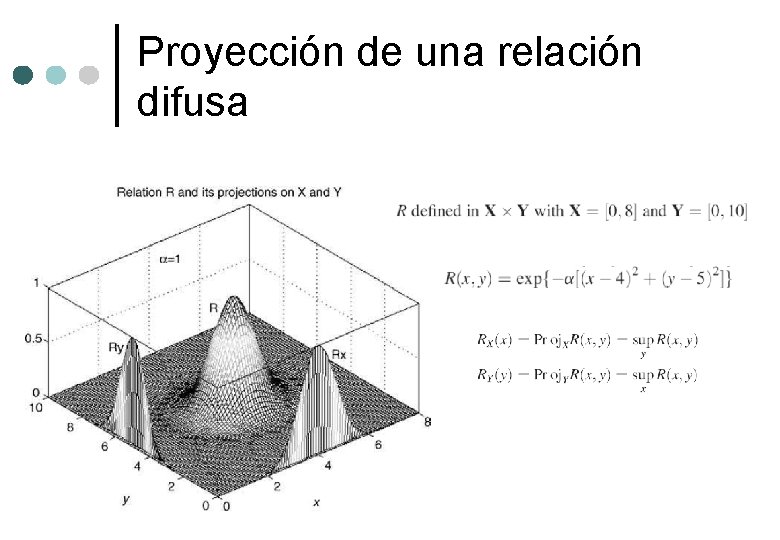
Proyecciones de conjuntos difusos Sea R un conjunto difuso en dos dimensiones definido en U V, entonces las proyecciones de R en U y en V estan definidas por: Proyección de R en U Proyección de R en V

Proyecciones de conjuntos difusos Proyección de R en U Proyección de R en V

Relación difusa ¢ Dados universos del discurso U y V, una relación difusa R es cualquier subconjunto del producto cartesiano de U y V: A B “Si A(u) Entonces B(v)”

Relación difusa ¢ Una relación difusa de la forma A B, denotada por R, del conjunto difuso A U al conjunto difuso B V, se define como un subconjunto difuso del producto cartesiano A B R se caracteriza por la función de membresía de 2 variables R(u, v)

Operaciones con relaciones difusas ¢ Unión: ¢ Intersección: ¢ Complemento ¢ Proyección

Proyección de una relación difusa

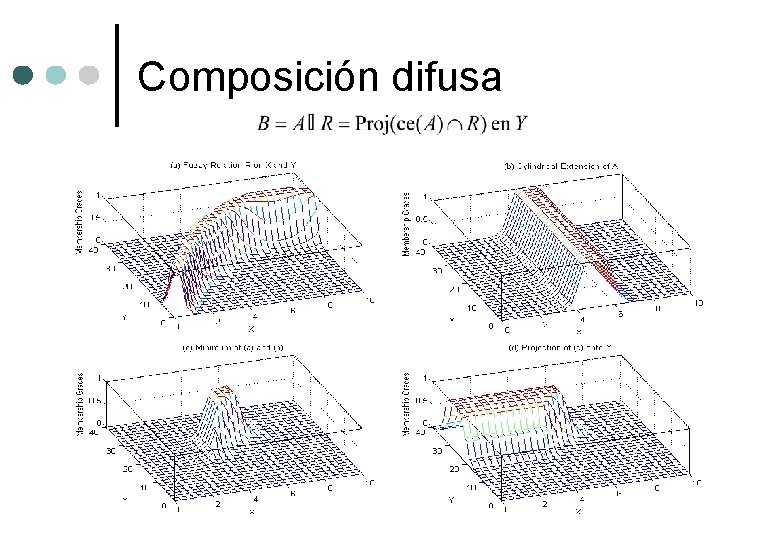
Composición difusa ¢ Sea A un conjunto difuso en X y R una relación difusa definida en X Y, la composicion difusa de A y R, que da como resultado el conjunto difuso B en Y, esta dada por: ¢ Utilizando composición max-min ¢ Utilizando composicion max-prod

Composición difusa

Variable lingüística En la descripción de sistemas centrados en lo humano generalmente se utilizan palabras en lugar de números para caracterizar los valores de las variables involucradas y sus relaciones, ejemplo: Variable Valor

Variable lingüística ¢ ¢ La función de una variable lingüística es proveer una estructura sistemática para caracterizar, de manera aproximada, los fenómenos complejos o no bien definidos La caracterización se realiza mediante el usos de palabras o sentencias expresadas en un lenguaje natural o sintético Se sacrifica precisión para ganar significancia Posibilita analizar fenómenos complejos de manera aproximada

Variable lingüística ¢ Una variable lingüística es aquella cuyos valores no son números sino palabras o sentencias (proposiciones) expresadas en un lenguaje natural o sintético (artificial)

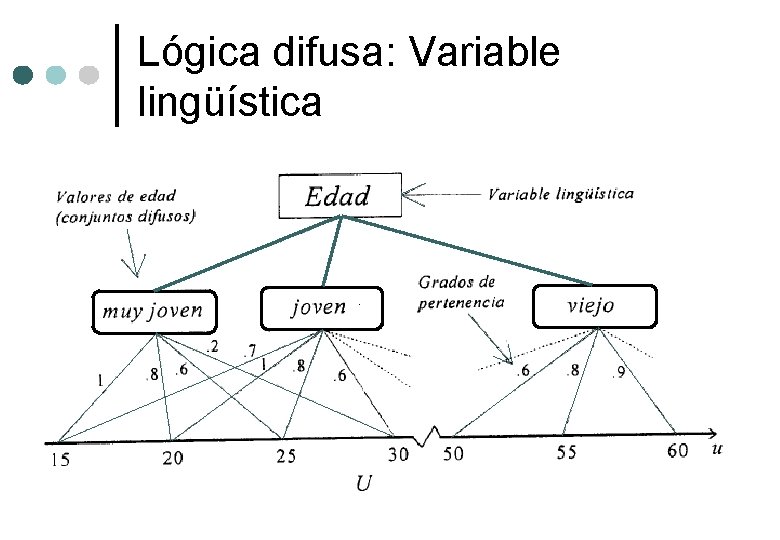
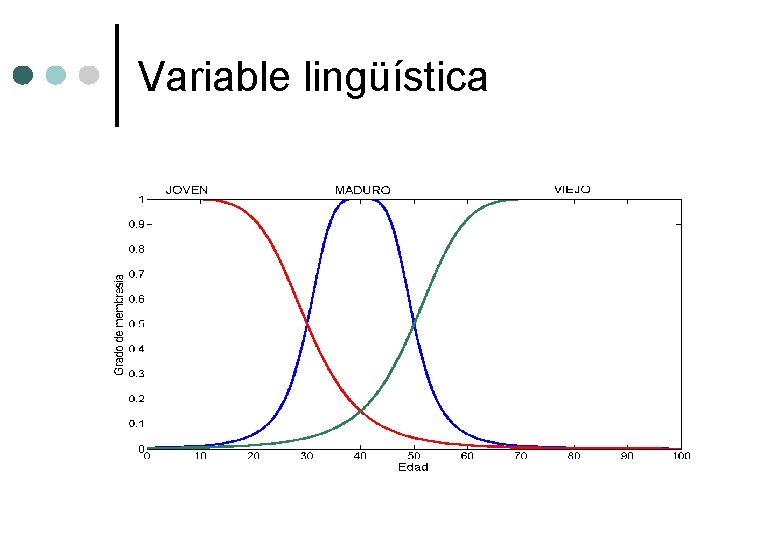
Variable lingüística ¢Los valores de una variable numérica son números: Edad = 65 ¢Los valores de una variable lingüística son palabras: Edad = Viejo ¢Un valor lingüístico es un conjunto difuso. ¢Los valores lingüísticos forman un conjunto de términos: T(Edad) = {joven, no muy joven, . . . maduro, no muy maduro, . . . viejo, no viejo, muy viejo, mas o menos viejo, . . . ni viejo ni joven, . . . }

Lógica difusa: Variable lingüística

Variable lingüística

Variable lingüística ¢ Una variable lingüística se caracteriza por la quinteta (x, T(x), U, G, M) l l l x es el nombre de la variable T(x) es el conjunto de términos o valores de x U es el universo del discurso, que esta asociado con la variable base u G es una regla sintáctica (gramática) para generar los nombres de los términos de x M es la regla semántica que asocia a cada valor de x su significado M(x), donde M es un subconjunto difuso de U

Sistema de Inferencias Difuso

Sistema de Inferencias Difuso: Fuzzificación Sistema MISO (multiple-input singleoutput) FIS: U Rn R, ¢ El proceso de fuzzificación mapea el vector real de entrada x = (x 1, x 2, …, xn ) Rn a conjuntos difusos de salida definidos en U. F = fuzzifier(x 0) ¢

Sistema de Inferencias Difuso: fuzzification a) Singleton fuzzification. This method maps the input x to a fuzzy singleton, F, with membership function: b) Approximated fuzzification: is a parameter that is determined in accordance with the context of each application.

Sistema de Inferencias Difuso: Evaluación de reglas SID MISO (Multiple-Inputs-Single-Output) Rj : Si x 1 es A 1 j AND x 2 es A 2 j AND ··· AND xn es Anj, entonces z es B j son las variables de entrada z es la variable de salida Son valores lingüísticos (conjuntos difusos) caracterizados por y j = 1, 2, …, m; m es el numero de reglas U 1, U 2, …, Un y V son los correspondientes universos del discurso

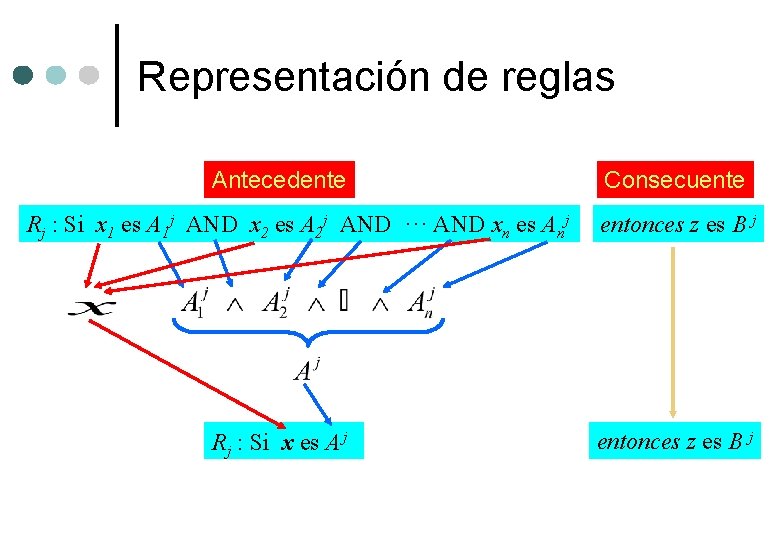
Representación de reglas Antecedente Rj : Si x 1 es A 1 j AND x 2 es A 2 j AND ··· AND xn es Anj Rj : Si x es A j Consecuente entonces z es B j

Base de reglas Base de Reglas R 1: si x es A 1, entonces z es B 1 OR R 2: si x es A 2, entonces z es B 2 OR Rn: si x es Am, entonces z es Bm

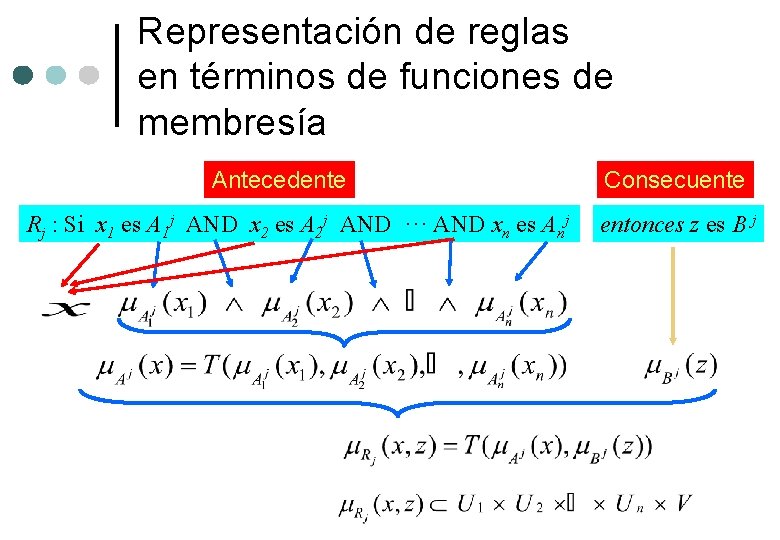
Representación de reglas en términos de funciones de membresía Antecedente Rj : Si x 1 es A 1 j AND x 2 es A 2 j AND ··· AND xn es Anj Consecuente entonces z es B j

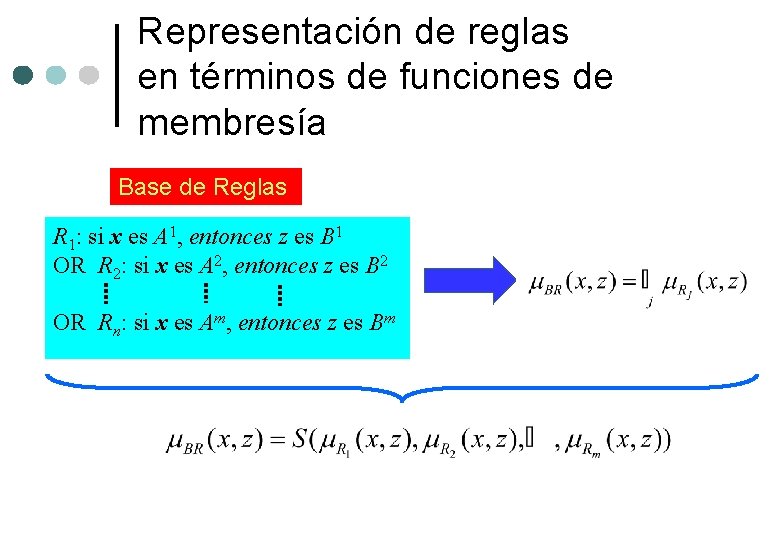
Representación de reglas en términos de funciones de membresía Base de Reglas R 1: si x es A 1, entonces z es B 1 OR R 2: si x es A 2, entonces z es B 2 OR Rn: si x es Am, entonces z es Bm

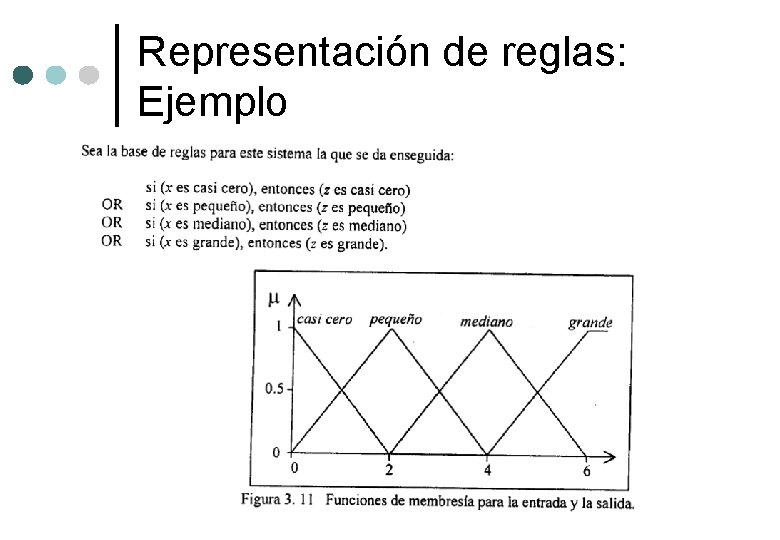
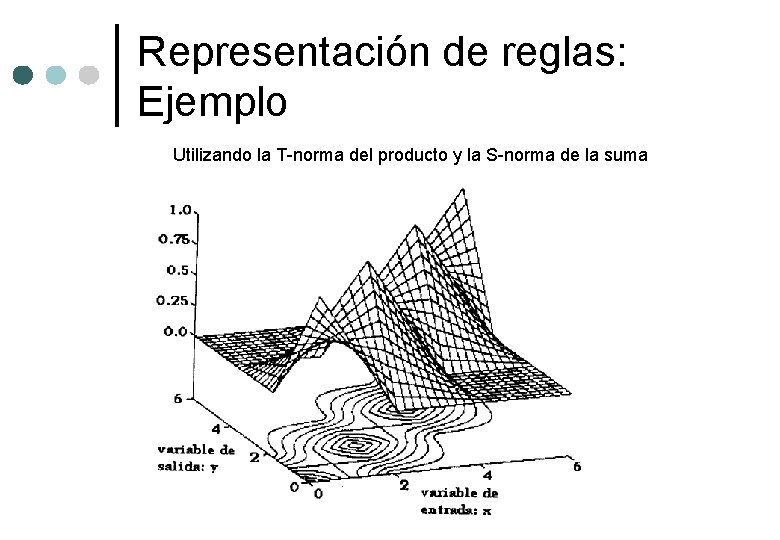
Representación de reglas: Ejemplo

Representación de reglas: Ejemplo Utilizando la T-norma del producto y la S-norma de la suma

Regla composicional de inferencias Una vez definida la base de reglas, ésta se puede utilizar para generar un conjunto difuso de salida dado un conjunto difuso de entrada ¢ Utilización de la regla composicional de inferencias ¢

Regla composicional de inferencias ¢ ¢ Sea BR(x, z) una base de reglas, entonces el conjunto difuso de salida B (z) inducido por el conjunto difuso de entrada A (x) esta dado por: Donde el símbolo representa la operacion de composición:

Regla composicional de inferencias Utilizando la regla max=min Utilizando la regla max=product

Razonamiento aproximado ¢ En lógica tradicional: Inferir la verdad de una proposición B a partir de una proposición A y la implicación A B l Ejemplo: A: “el jitomate esta rojo” B: “el jitomate esta maduro” es decir, si A B significa que si la sentencia A es verdadera entonces la sentencia B también es verdadera l

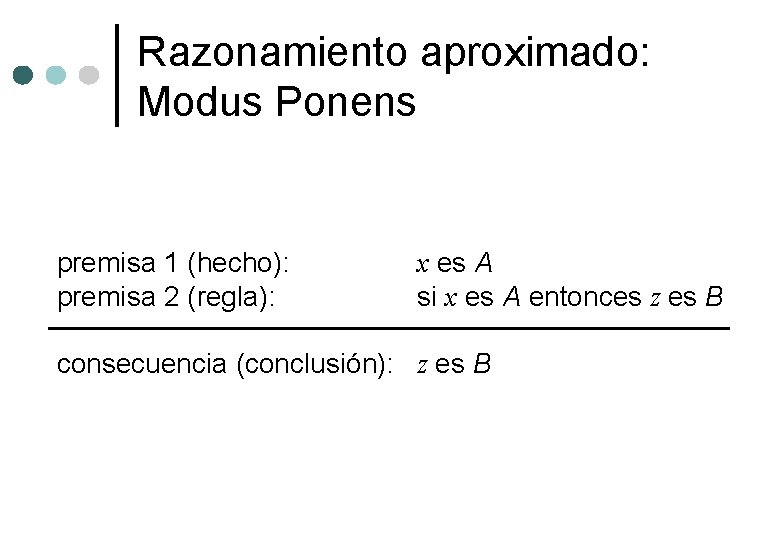
Razonamiento aproximado: Modus Ponens premisa 1 (hecho): premisa 2 (regla): x es A si x es A entonces z es B consecuencia (conclusión): z es B

Razonamiento aproximado ¢ En lógica difusa: Inferir la verdad de una proposición B’ a partir de una proposición A’ y la implicación A B l Ejemplo: A’: “el jitomate esta mas o menos rojo” B’: “el jitomate esta mas o menos maduro” entonces si A B significa que si la sentencia A’ es verdadera entonces la sentencia B’ también es verdadera l

Razonamiento aproximado Modus Ponens Generalizado premisa 1 (hecho): premisa 2 (regla): x es A’ si x es A entonces z es B consecuencia (conclusión): z es B’ en donde la sentencia A’ esta cercana a la sentencia A y la sentencia B’ esta cercana a la sentencia B

Evaluación de reglas en términos de funciones de membresía Rj : If x is Aj and y is Bj then z is Cj

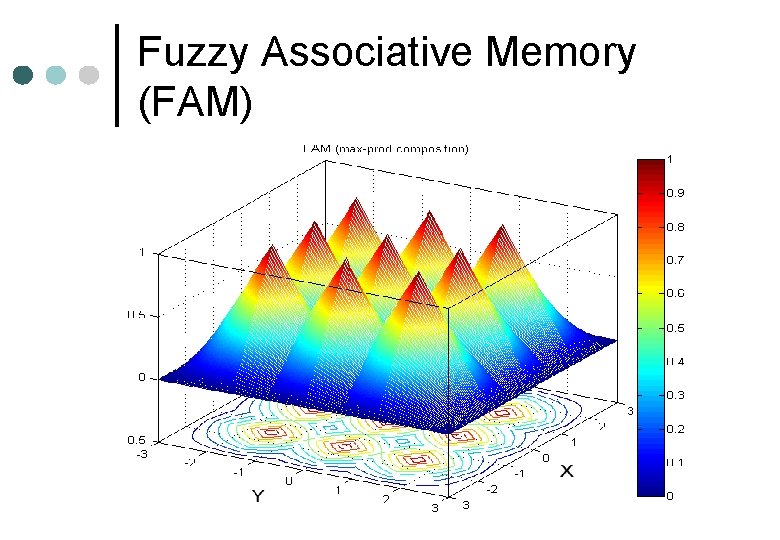
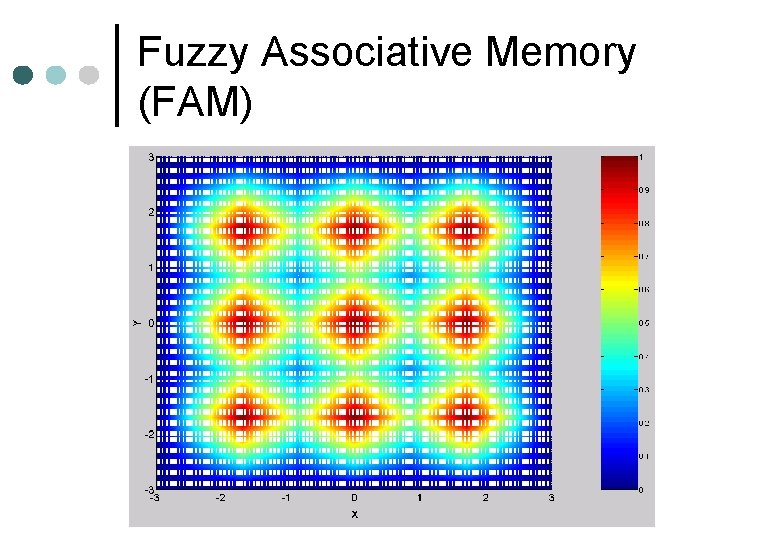
Fuzzy Associative Memory (FAM)

Fuzzy Associative Memory (FAM)

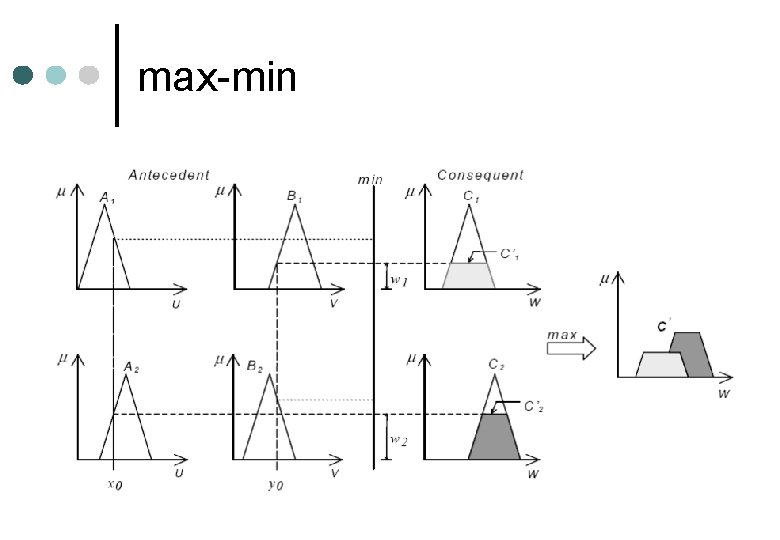
max-min

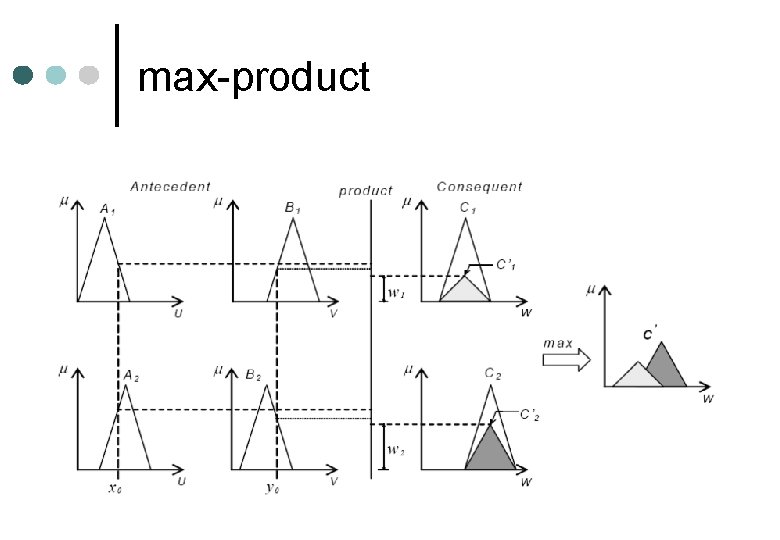
max-product

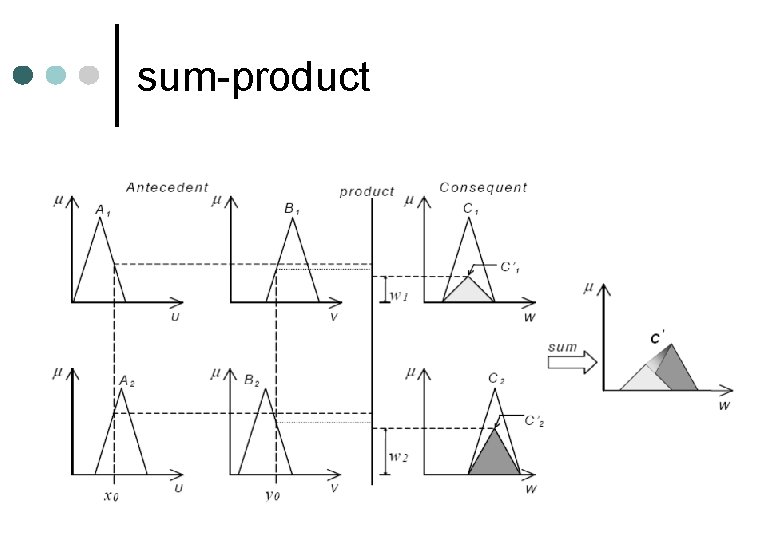
sum-product

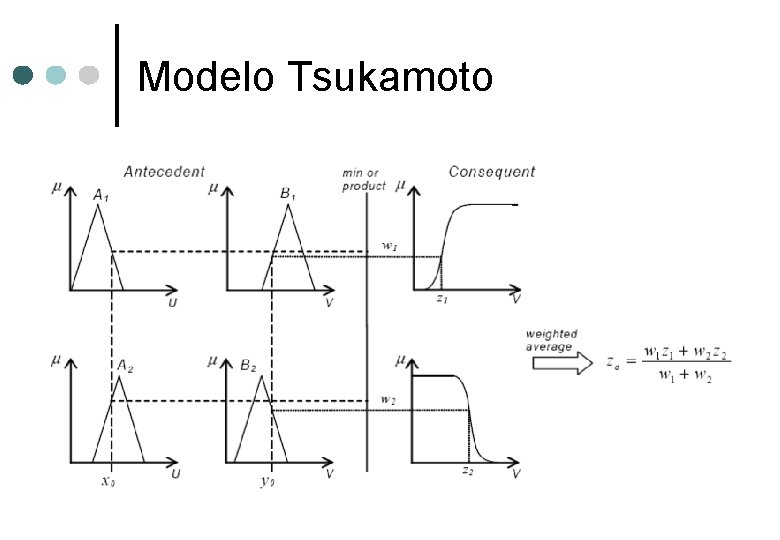
Modelos de SID Modelo Mandami ¢ Modelo Sugeno-Takagi ¢ Modelo Tsukamoto ¢

Modelo Mandani ¢ Utiliza conjuntos difusos tanto en la parte del antecedente de las reglas como en el consecuente de las mismas.

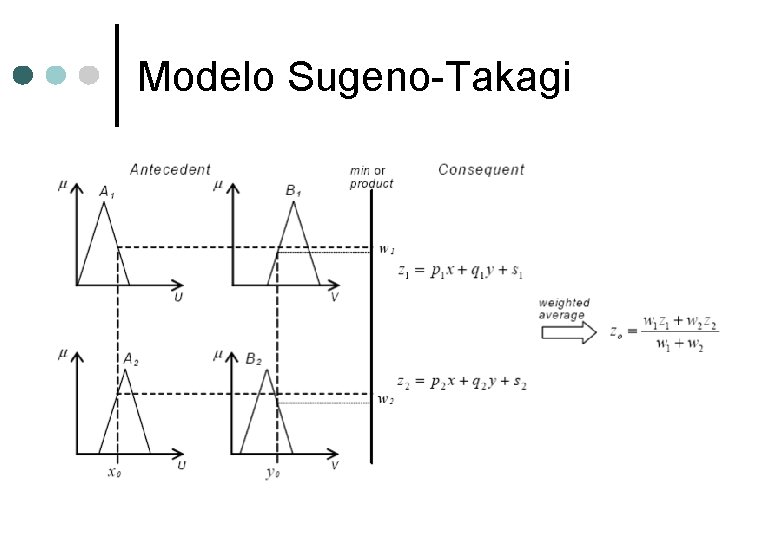
Modelo Sugeno-Takagi ¢ Reglas de la forma: ¢ f (·) es cualquier función de las variables de entrada f (·) = polinomio de grado 1, SID Sugeno de grado 1 f (·) = constante, SID Sugeno de grado 0 ¢ ¢

Modelo Sugeno-Takagi

Modelo Tsukamoto

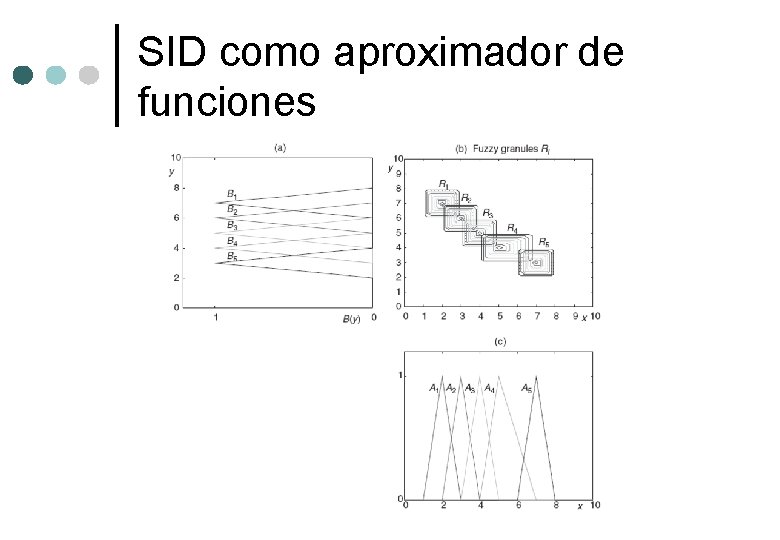
Un SID es un aproximador universal de funciones ¢ ¢ A fuzzy rule-base system, FRBS = ( ab, R, T, S, DEF), is a family of fuzzy systems with membership functions ab a fuzzy rule base R, the t-norm, for fuzzy aggregation T (i. e. operations within one rule), the s-norm for fuzzy composition S (i. e. operations among rules), and the defuzzification method DEF. Defuzzification consists of the conversion of the fuzzy output into a single crisp output. Any given fuzzy system FS FRBS is a universal approximator according to a theorem. Let the fuzzy rule-based system FRBS be the set of all fuzzy systems FS and f: U Rn R be a continuous function defined on a universe of discourse U. For each > 0, there exists a FSe FRBS such that sup { f(x) - FSe(x) , x U }

SID como aproximador de funciones

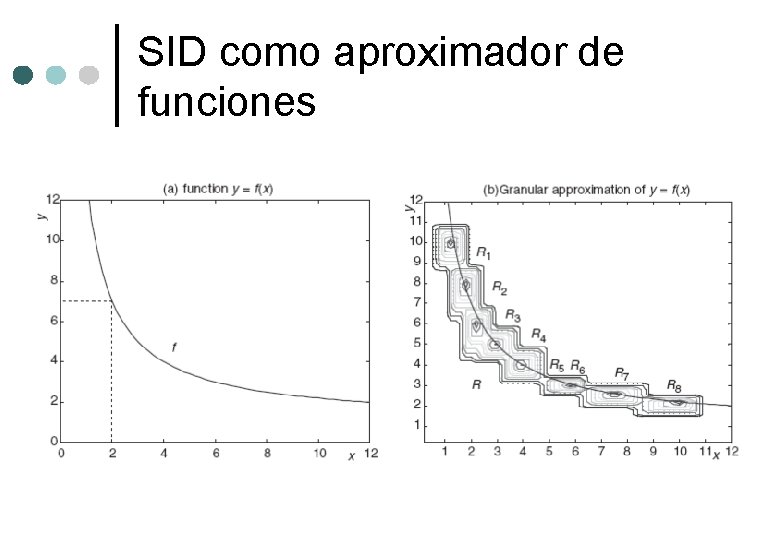
SID como aproximador de funciones

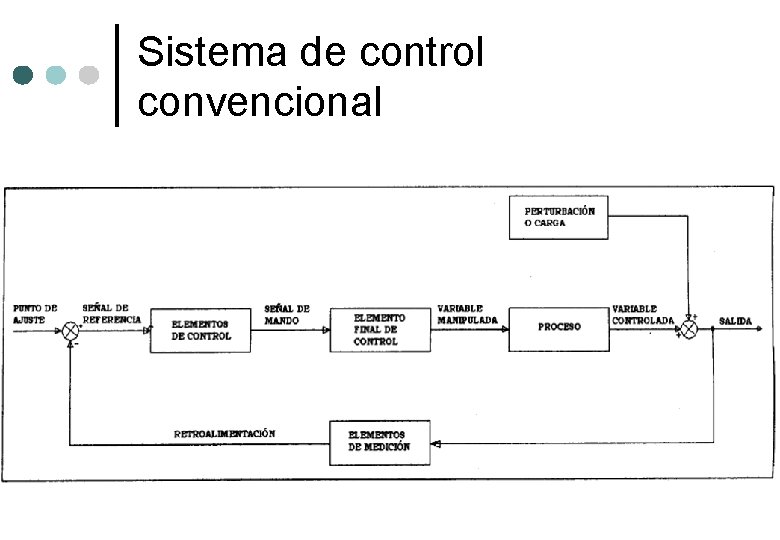
Sistema de control convencional

Tradicional PID control A traditional PID controller in continuous form can be expressed as:

Tradicional PID control A traditional PID controller in digital form can be expressed as:

Tradicional PID control To avoid derivative kick and reduce overshoot

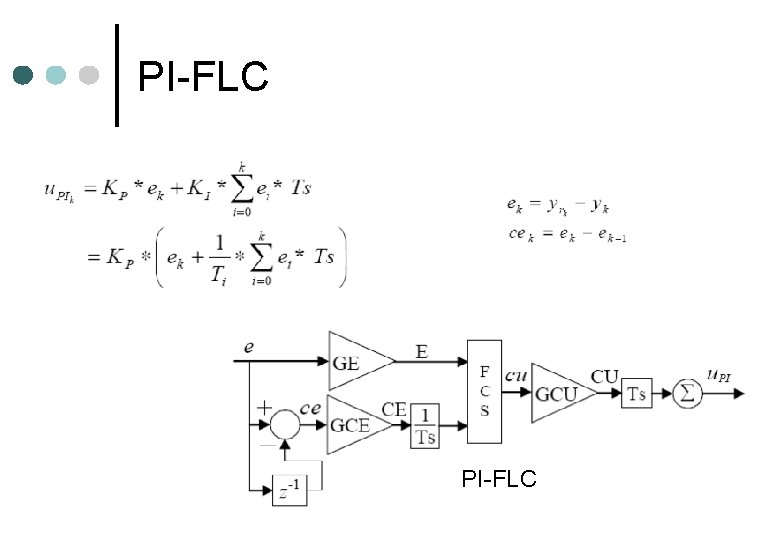
PI-FLC

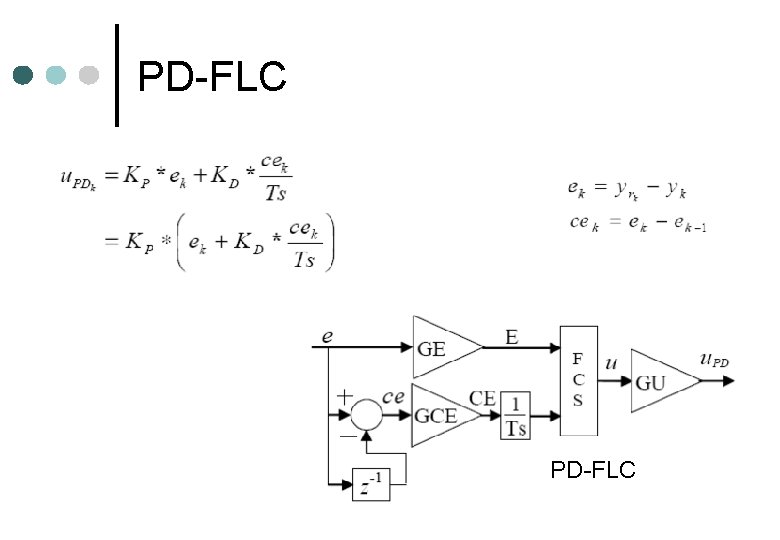
PD-FLC

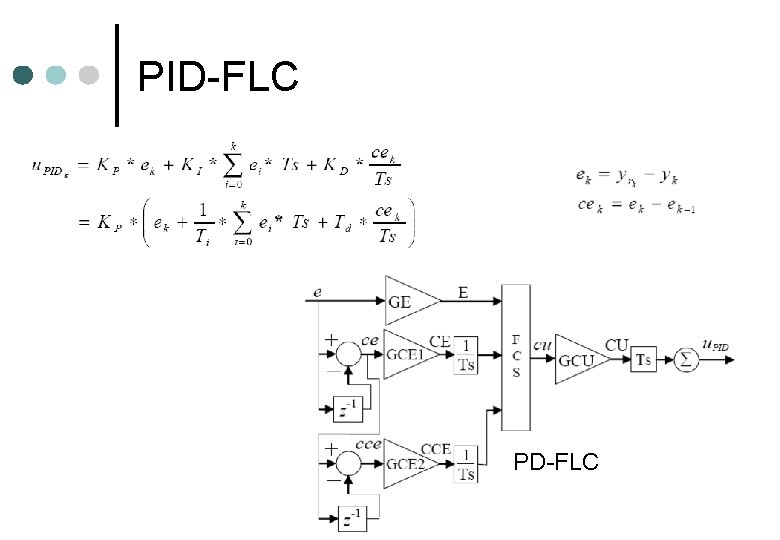
PID-FLC PD-FLC

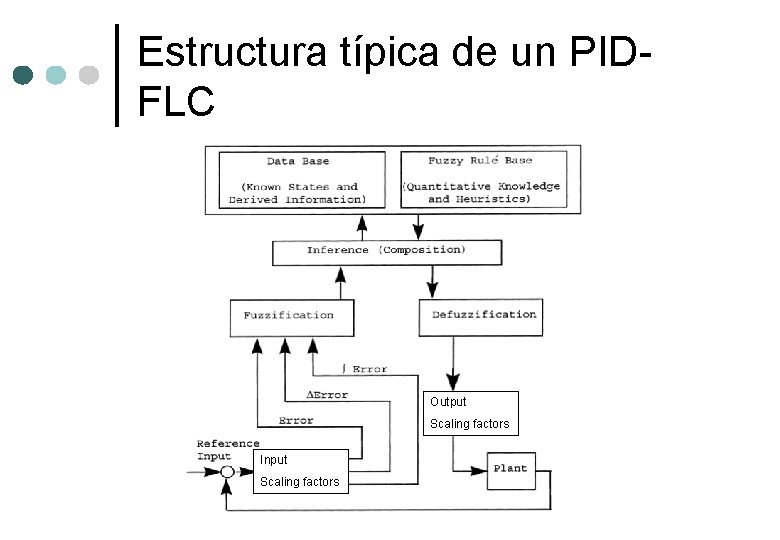
Estructura típica de un PIDFLC Output Scaling factors Input Scaling factors

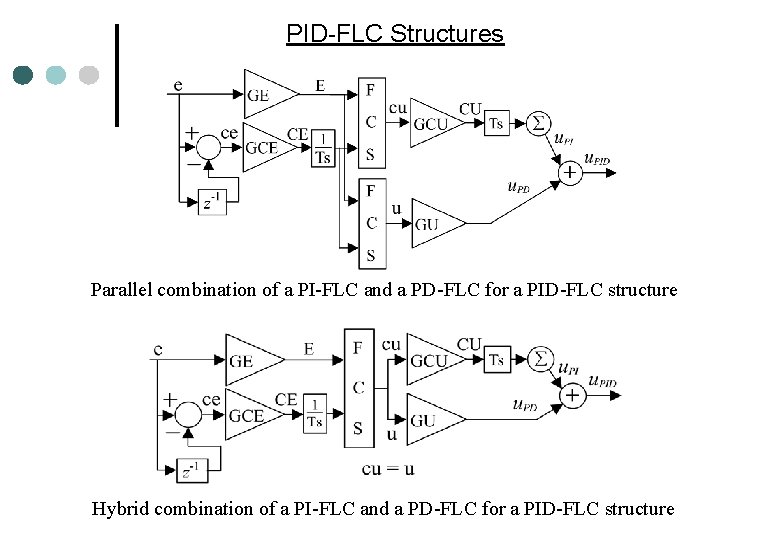
PID-FLC Structures Parallel combination of a PI-FLC and a PD-FLC for a PID-FLC structure Hybrid combination of a PI-FLC and a PD-FLC for a PID-FLC structure