Secure Computation Lecture 5 Arpita Patra Recap Scope

Secure Computation (Lecture 5) Arpita Patra

Recap >> Scope of MPC > models of computation > network models > modelling distrust (centralized/decentralized adversary) > modelling adversary > Various Parameters/questions asked in MPC >> Defining Security of MPC > Ideal World & Real world > Indistinguishability of the view of adversary in real and ideal (with the help of simulator) world > Indistinguishability of the joint dist. of the output of the honest parties and the view of adversary in real and ideal (with the help of simulator) world.

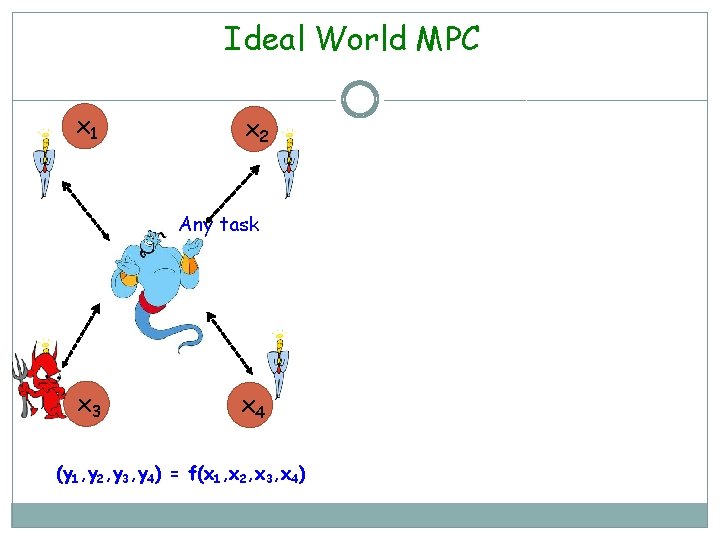
Ideal World MPC x 1 x 2 Any task x 3 x 4 (y 1, y 2, y 3, y 4) = f(x 1, x 2, x 3, x 4)

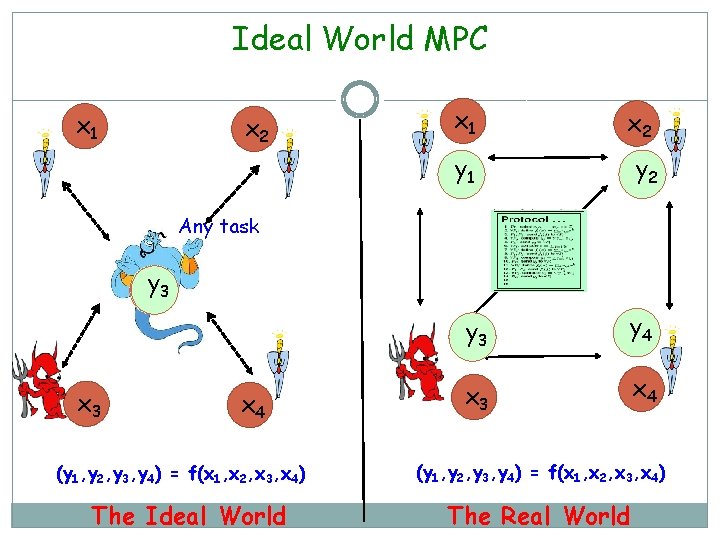
Ideal World MPC x 1 x 2 y 1 y 2 Any task y 2134 x 3 x 4 (y 1, y 2, y 3, y 4) = f(x 1, x 2, x 3, x 4) The Ideal World y 3 y 4 x 3 x 4 (y 1, y 2, y 3, y 4) = f(x 1, x 2, x 3, x 4) The Real World

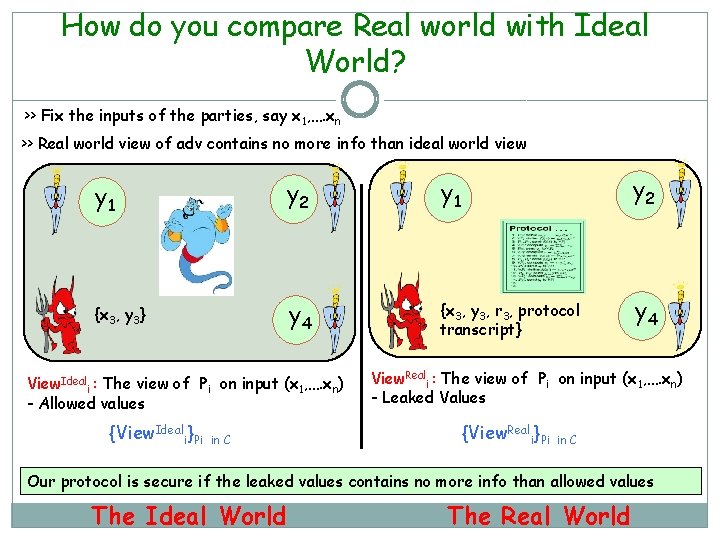
How do you compare Real world with Ideal World? >> Fix the inputs of the parties, say x 1, …. xn >> Real world view of adv contains no more info than ideal world view y 1 y 2 {x 3, y 3} y 4 {x 3, y 3, r 3, protocol transcript} y 4 View. Ideali : The view of Pi on input (x 1, …. xn) - Allowed values {View. Ideali}Pi in C View. Reali : The view of Pi on input (x 1, …. xn) - Leaked Values {View. Reali}Pi in C Our protocol is secure if the leaked values contains no more info than allowed values The Ideal World The Real World

Real world (leaked values) vs. Ideal world (allowed values) y 1 y 2 {x 3, y 3} y 4 {x 3, y 3, r 3, protocol transcript} y 4 >> If leaked values can be efficiently computed from allowed values. >> Such an algorithm is called SIMULATOR (simulates the view of the adversary in the real protocol). >> It is enough if SIM creates a view of the adversary is “close enough” to the real view so that adv. can not distinguish from its real view. The Ideal World The Real World

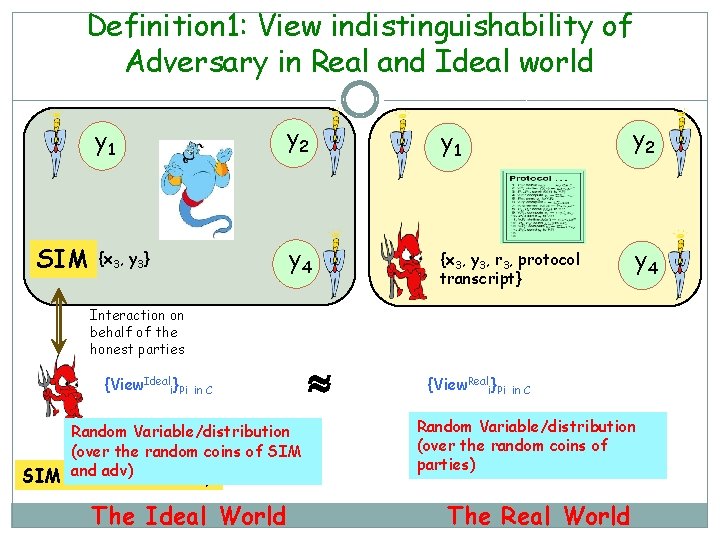
Definition 1: View indistinguishability of Adversary in Real and Ideal world SIM y 1 y 2 {x 3, y 3} y 4 {x 3, y 3, r 3, protocol transcript} y 4 Interaction on behalf of the honest parties {View. Ideali}Pi in C Random Variable/distribution (over the random coins of SIM adv)Adversary SIM: and Ideal The Ideal World {View. Reali}Pi in C Random Variable/distribution (over the random coins of parties) The Real World

Definition 2: Indistinguishability of Joint Distributions of Output and View >> Joint distribution of output & view of the honest & corrupted parties in both the worlds can not be told apart Output. Ideali : The output of Pi on input (x 1, …. xn) when Pi is honest. Output. Reali : The output of Pi on input (x 1, …. xn) when Pi is honest. View. Ideali : As defined before when Pi is corrupted. View. Reali : As defined before when Pi is corrupted. [ {View. Ideali}Pi in C , {Output. Ideali}Pi in H ] [ {View. Reali}Pi in C , {Output. Reali}Pi in H ] >> First note that this def. subsumes the previous definition (stronger) >> Captures randomized functions as well The Ideal World The Real World

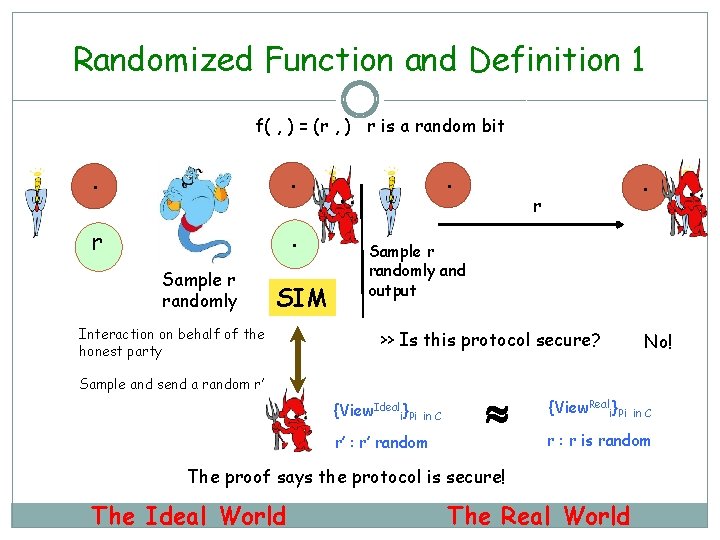
Randomized Function and Definition 1 f( , ) = (r , ) r is a random bit . . r . Sample r randomly SIM Interaction on behalf of the honest party . . r Sample r randomly and output >> Is this protocol secure? Sample and send a random r’ {View. Ideali}Pi in C r’ : r’ random {View. Reali}Pi in C r : r is random The proof says the protocol is secure! The Ideal World No! The Real World

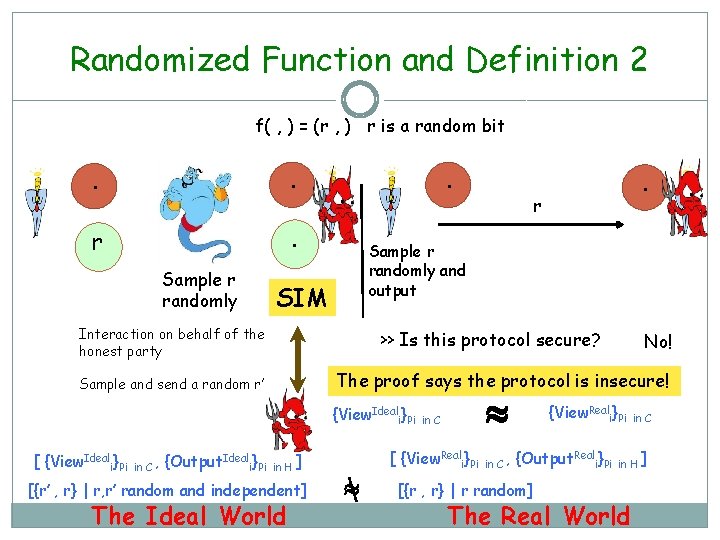
Randomized Function and Definition 2 f( , ) = (r , ) r is a random bit . . r . Sample r randomly . SIM >> Is this protocol secure? {View. Ideali}Pi {Output. Ideali}Pi No! The proof says the protocol is insecure! Sample and send a random r’ in C , r Sample r randomly and output Interaction on behalf of the honest party [ {View. Ideali}Pi . in H ] [{r’ , r} | r, r’ random and independent] The Ideal World in C [ {View. Reali}Pi in C , {View. Reali}Pi {Output. Reali}Pi [{r , r} | r random] in C in H ] The Real World

Definition 1 is Enough! >> For deterministic Functions: {{View. Ideali}Pi in C , {Output { {View. Ideali}Pi } Ideal } i Pi in H {x 1, . , xn , k} } in C {x 1, . , xn , k} {{View. Reali}Pi in C , {Output {{View. Reali}Pi Real } i Pi in H } {x 1, . . xn , k} } in C {x 1, . , xn , k} > View of the adversary and output are NOT co-related. > We can separately consider the distributions > Output of the honest parties are fixed for inputs >> For randomized functions: > We can view it as a deterministic function where the parties input randomness (apart from usual inputs). Compute f((x 1, r 1), (x 2, r 2)) to compute g(x 1, x 2; r) where r 1+r 2 can act as r.

Making Indistinguishability Precise Notations: o Security parameter k (natural number) o We wish security to hold for all inputs of all lengths, as long as k is large enough Definition (Function �is negligible): If for every polynomial p(�) there exists an N such that for all k > N we have �(k) < 1/p(k) Definition (Probability ensemble X={X(a, k)}): o Infinite series, indexed by a string a and natural k o Each X(a, k) is a random variable In our context: o X(x 1, . , xn , k) = { {View. Reali}Pi in C }{x 1, . , xn , k} (Probability space: randomness of parties) o Y(x 1, . , xn , k) = { {View. Ideali}Pi in C }{x 1, . , xn , k} (Probability space: randomness of the corrupt parties and simulator)

Computational Indistinguishability o X(x 1, . , xn , k) = { {View. Reali}Pi in C }{x 1, . , xn , k} (Probability space: randomness of parties) o Y(x 1, . , xn , k) = { {View. Ideali}Pi in C }{x 1, . , xn , k} (Probability space: randomness of the corrupt parties and simulator) Definition (Computational indistinguishability of X = {X(a, k)} � c Y = {Y(a, k)}) For every polynomial-time distinguisher* D there exists a negligible function � such that for every a and all large enough k’s: |Pr[D(X(a, k) = 1 ] - Pr[D(Y(a, k) = 1 ]| < �(k) Alternative def. Adv. D (X, Y) = The prob of D guessing the correct distribution |Adv. D (X, Y)| < ½ + �(k) For our case a: (x 1, . , xn) distinguisher D = Real Adv A

Statistical Indistinguishability o X(x 1, . , xn , k) = { {View. Reali}Pi in C }{x 1, . , xn , k} (Probability space: randomness of parties) o Y(x 1, . , xn , k) = { {View. Ideali}Pi in C }{x 1, . , xn , k} (Probability space: randomness of the corrupt parties and simulator) Definition (Statistical indistinguishability of X = {X(a, k)} �s Y = {Y(a, k)}) For every* distinguisher D there exists a negligible function � such that for every a and all large enough k’s: |Pr[D(X(a, k) = 1 ] - Pr[D(Y(a, k) = 1 ]| < �(k) Alternative def. Adv. D (X, Y) = The prob of D guessing the correct distribution |Adv. D (X, Y)| < ½ + �(k) For our case a: (x 1, . , xn) May have unbounded power

Perfect Indistinguishability o X(x 1, . , xn , k) = { {View. Reali}Pi in C }{x 1, . , xn , k} (Probability space: randomness of parties) o Y(x 1, . , xn , k) = { {View. Ideali}Pi in C }{x 1, . , xn , k} (Probability space: randomness of the corrupt parties and simulator) Definition (Perfect indistinguishability of X = {X(a, k)} �P Y = {Y(a, k)}) For every* distinguisher D such that for every a and for all k: |Pr[D(X(a, k) = 1 ] - Pr[D(Y(a, k) = 1 ]| = 0 Alternative def. Adv. D (X, Y) = The prob of D guessing the correct distribution |Adv. D (X, Y)| = ½ For our case a: (x 1, . , xn) May have unbounded power

Definition Applies for Dimension 2 (Networks) Dimension 3 (Distrust) Dimension 4 (Adversary) Complete Centralized Threshold/nonthreshold Synchronous Polynomially Bounded and unbounded powerful Semi-honest Static

What is so great about the definition paradigm? >> One definition for all > Sum: (x 1 + x 2 + … + xn) = f(x 1, x 2, … , xn) > OT: (- , xb) = f((x 1, x 2 ), b) > BA: (y , y, …, y) = f(x 1, x 2, … , xn): y = majority(x 1, x 2, … , xn)/default value >> Easy to tweak the ideal world and weaken/strengthen security Real world protocol achieves whatever ideal world achieves >> Coming up with the right ideal world is tricky and requires skill > Will have fun with it in malicious world!

Information Theoretic MPC with Semi-honest Adversary and honest majority [BGW 88] Dimension 1 (Models of Computation) Arithmetic Dimension 2 (Networks) Dimension 3 (Distrust) Dimension 4 (Adversary) Complete Centralized Threshold (t) Synchronous Unbounded powerful Semi-honest Static Michael Ben-Or, Shafi Goldwasser, Avi Wigderson: Completeness Theorems for Non-Cryptographic Fault-Tolerant Distributed Computation (Extended Abstract). STOC 1988.

(n, t) - Secret Sharing Scheme [Shamir 1979, Blackley 1979] Secret s Dealer

(n, t) - Secret Sharing Scheme [Shamir 1979, Blackley 1979] Sharing Phase v 1 v 2 Secret s v 3 … Dealer vn

(n, t) - Secret Sharing Scheme [Shamir 1979, Blackley 1979] Sharing Phase v 1 v 2 Secret s v 3 Reconstruction Phase … Dealer vn Less than t +1 parties have no info’ about the secret

(n, t) - Secret Sharing Scheme [Shamir 1979, Blackley 1979] Sharing Phase v 1 v 2 Secret s v 3 Reconstruction Phase … Dealer vn Secret s t +1 parties can reconstruct the secret

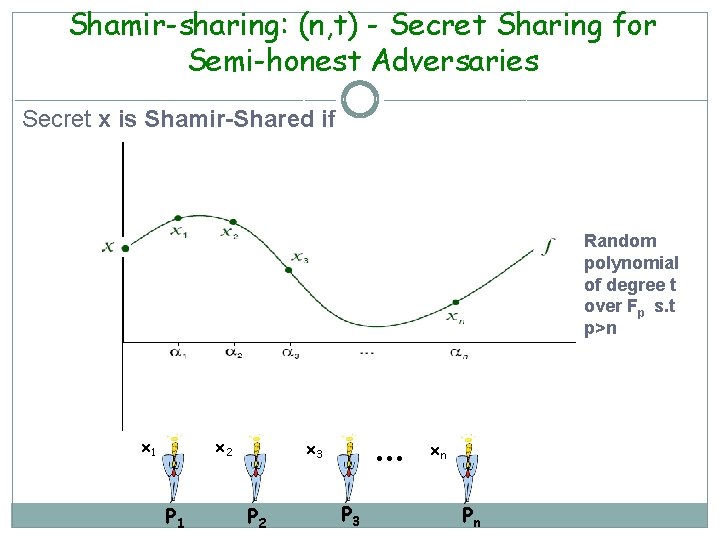
Shamir-sharing: (n, t) - Secret Sharing for Semi-honest Adversaries Secret x is Shamir-Shared if Random polynomial of degree t over Fp s. t p>n x 1 x 2 P 1 … x 3 P 2 P 3 xn Pn

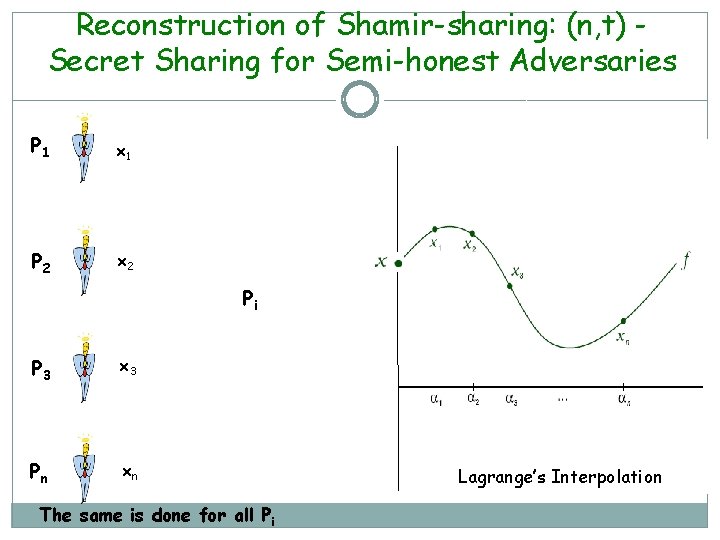
Reconstruction of Shamir-sharing: (n, t) Secret Sharing for Semi-honest Adversaries P 1 x 1 P 2 x 2 Pi P 3 x 3 Pn xn The same is done for all Pi Lagrange’s Interpolation

Shamir-sharing Properties Property 1: Any (t+1) parties have ‘complete’ information about the secret. Property 2: Any t parties have ‘no’ information about the secret. Pr[secret =s before secret sharing] – Pr[secret =s after secret sharing] = 0 >> Both proof can be derived from Lagrange’s Interpolation.

Lagrange’s Interpolation >> Assume that h(x) is a polynomial of degree at most t and C is a subset of F p of size t+1 >> Assume for simplicity C = {1, ……, t+1} Theorem: h(x) can be written as where Proof: Both LHS and RHS evaluates to h(i) for every i in C Both LHS and RHS has degree at most t >> Poly of degree t >> At i, it evaluates to 1 >> At any other point, it gives 0. Consider LHS – RHS: LHS - RHS evaluates to 0 for every i in C and has degree at most t More zeros (roots) than degree LHS = RHS Zero polynomial!

Lagrange’s Interpolation where Theorem: h(x) can be written as >> Poly of degree t >> At i, it evaluates to 1 >> At any other point, it gives 0. >> are public polynomials >> are public values, denote by ri >> Can be written as the linear combination of h(i)s The combiners are (recombination vector): r 1, …. rt+1 Property 1: Any (t+1) parties have ‘complete’ information about the secret. C = {1, ……, t+1}

Lagrange’s Interpolation Property 2: Any t parties have ‘no’ information about the secret. Pr[secret =s before secret sharing] – Pr[secret =s after secret sharing] = 0 Proof: For any secret s from Fp if we sample f(x) of degree at most t randomly s. t. f(0) = s and consider the following distribution for any C that is subset of Fp {0} and of size t : ( {f(i)}i in C ) For a fixed s, t coefficients from Fpt uniform distribution in Fpt A unique element from the above distribution If not then two different sets of t+1 values will define the same polynomial

Lagrange’s Interpolation Property 2: Any t parties have ‘no’ information about the secret. Pr[secret =s before secret sharing] – Pr[secret =s after secret sharing] = 0 Proof: For any secret s from Fp if we sample f(x) of degree at most t randomly s. t. f(0) = s and consider the following distribution for any C that is subset of Fp {0} and of size t : ( {f(i)}i in C ) For a fixed s, t coefficients from Fpt fs : Fp t Uniform distribution uniform distribution in Fpt A unique element from the above distribution bijective Fp t Uniform distribution For every s, uniform dist and independent of dist. of s

Lagrange’s Interpolation Property 2: Any t parties have ‘no’ information about the secret. Pr[secret =s before secret sharing] – Pr[secret =s after secret sharing] = 0 Proof:

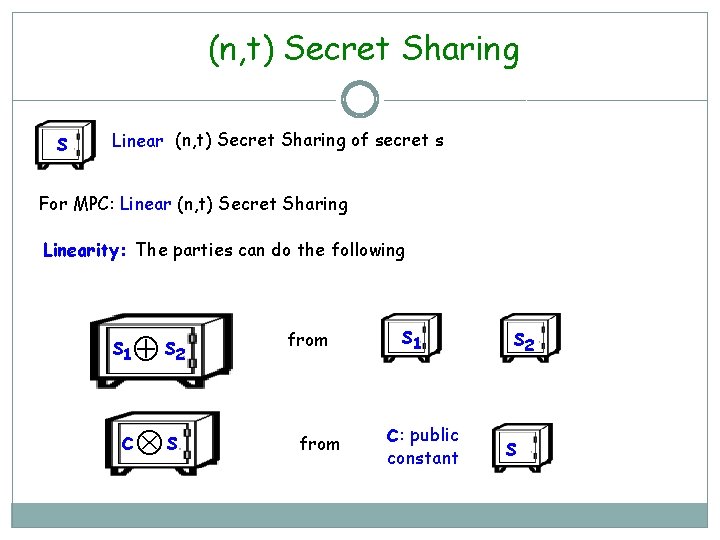
(n, t) Secret Sharing s Linear: (n, t) Secret Sharing of secret s For MPC: Linear (n, t) Secret Sharing Linearity: The parties can do the following s 1 s 2 c s from s 1 c: public constant s 2 s

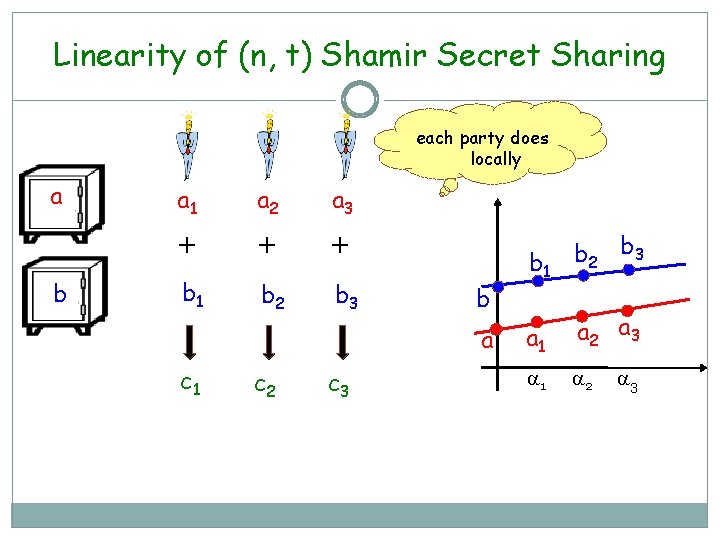
Linearity of (n, t) Shamir Secret Sharing each party does locally a b a 1 a 2 a 3 + + + b 1 b 2 b 3 b a c 1 c 2 c 3 b 1 b 2 b 3 a 1 a 2 a 3 1 2 3

Linearity of (n, t) Shamir Secret Sharing a b a 1 a 2 a 3 + + + b 1 b 2 b 3 a+b b a a b c 1 c 2 c 3 c 1 c 2 b 1 b 2 b 3 a 1 a 2 a 3 1 2 3 Addition is Absolutely free

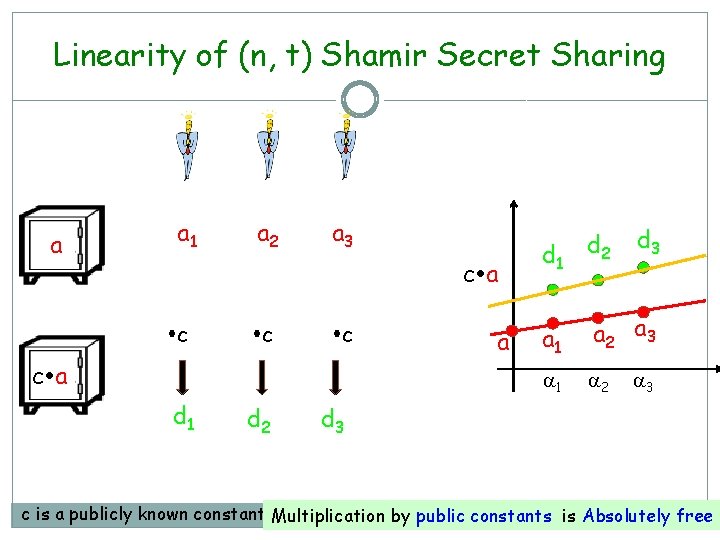
Linearity of (n, t) Shamir Secret Sharing a a 1 a 2 a 3 c a c c c c a d 1 d 2 a d 3 d 1 d 2 a 1 a 2 a 3 1 2 3 d 3 c is a publicly known constant Multiplication by public constants is Absolutely free

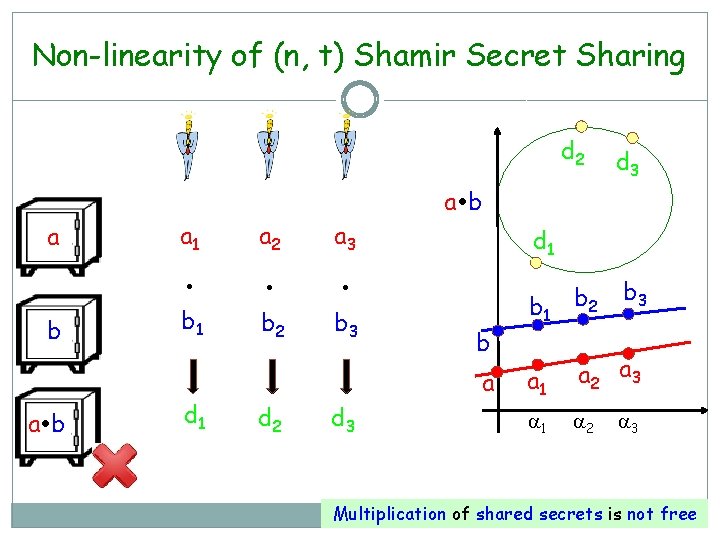
Non-linearity of (n, t) Shamir Secret Sharing d 2 d 3 a b a b a 1 a 2 a 3 b 1 b 2 b 3 d 1 b a d 2 d 3 b 1 b 2 b 3 a 1 a 2 a 3 1 2 3 Multiplication of shared secrets is not free

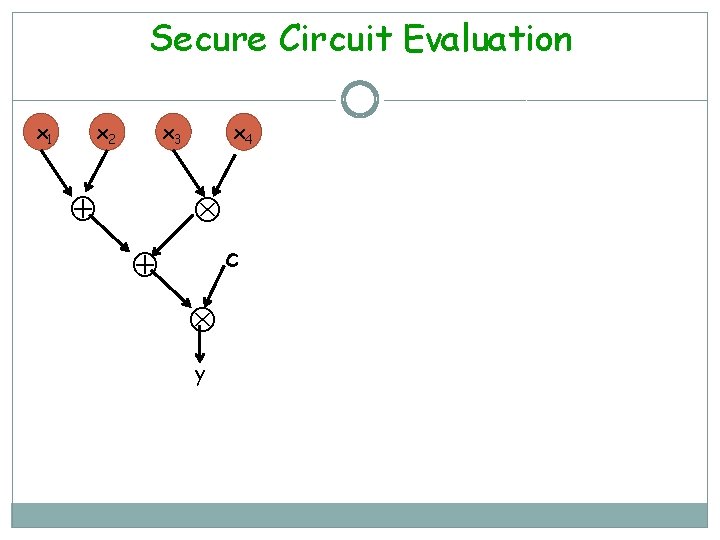
Secure Circuit Evaluation x 1 x 2 x 3 x 4 c y

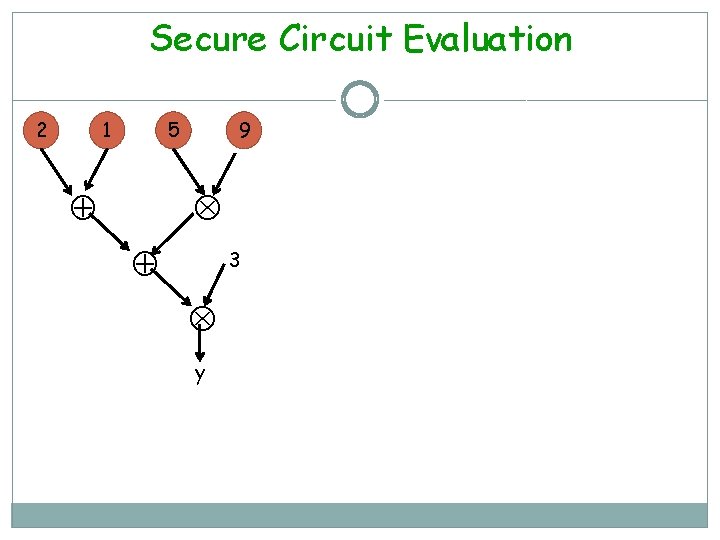
Secure Circuit Evaluation 2 1 5 9 3 y

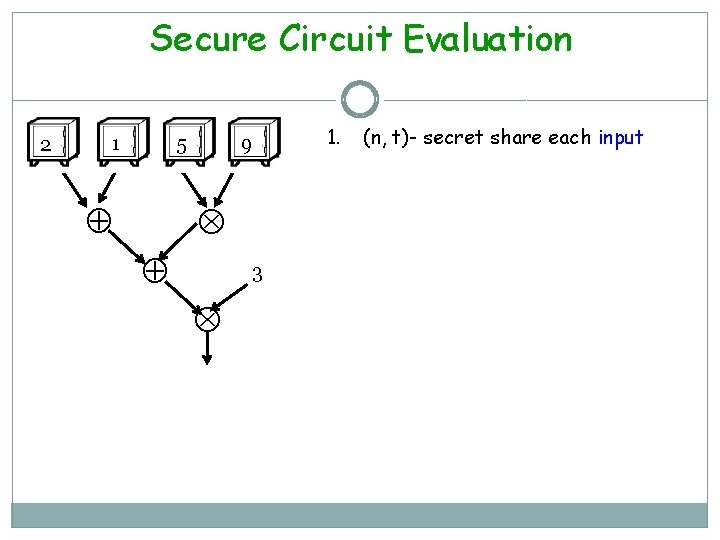
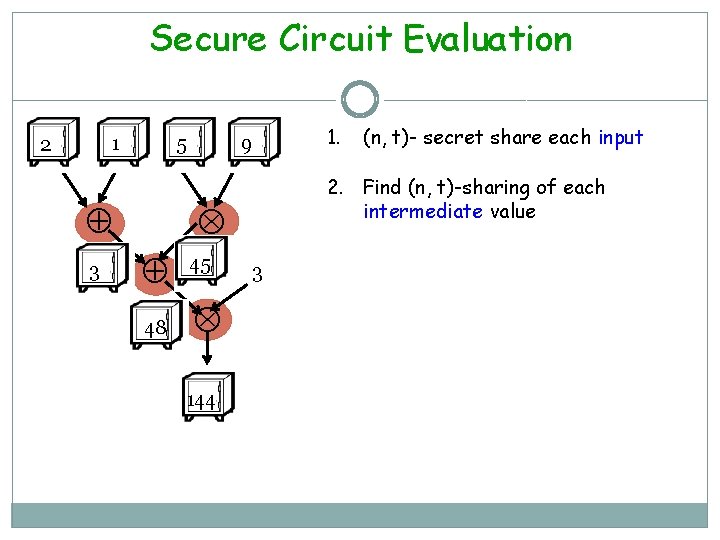
Secure Circuit Evaluation 2 1 5 9 3 1. (n, t)- secret share each input

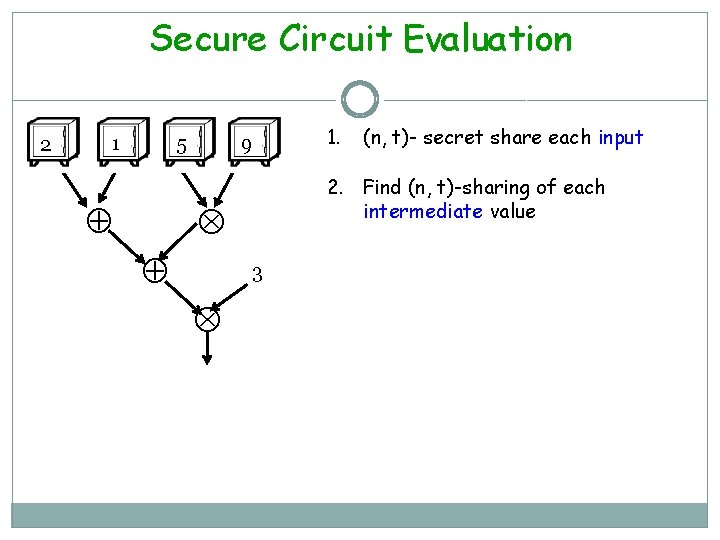
Secure Circuit Evaluation 2 1 5 9 3 (n, t)- secret share each input 2. Find (n, t)-sharing of each intermediate value 1.

Secure Circuit Evaluation 1 2 5 3 9 45 48 144 (n, t)- secret share each input 2. Find (n, t)-sharing of each intermediate value 1. 3

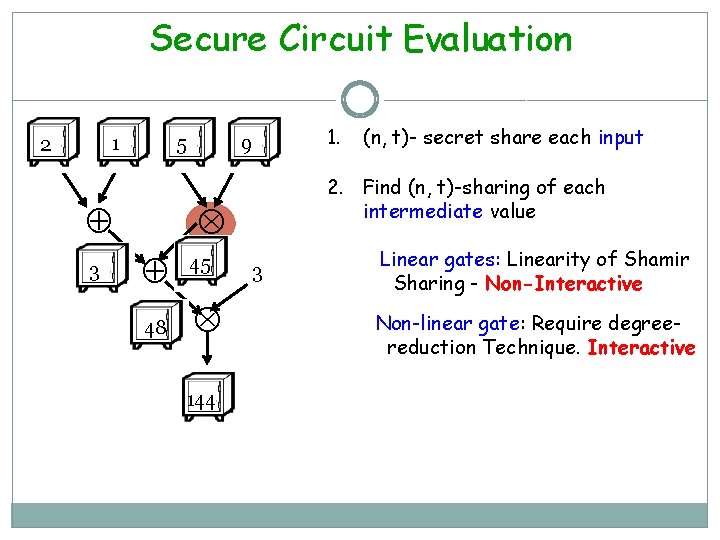
Secure Circuit Evaluation 1 2 5 3 9 48 144 (n, t)- secret share each input 2. Find (n, t)-sharing of each intermediate value 45 1. 3 Linear gates: Linearity of Shamir Sharing - Non-Interactive

Secure Circuit Evaluation 1 2 5 3 9 48 144 (n, t)- secret share each input 2. Find (n, t)-sharing of each intermediate value 45 1. 3 Linear gates: Linearity of Shamir Sharing - Non-Interactive Non-linear gate: Require degreereduction Technique. Interactive

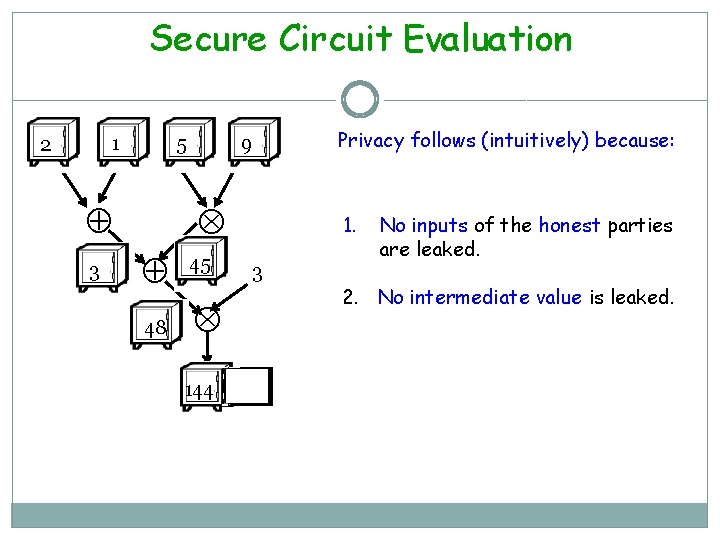
Secure Circuit Evaluation 1 2 5 3 9 45 48 144 Privacy follows (intuitively) because: 1. 3 No inputs of the honest parties are leaked. 2. No intermediate value is leaked.