Cryptography Lecture 3 Arpita Patra Arpita Patra Recall

Cryptography Lecture 3 Arpita Patra © Arpita Patra

Recall >> Study of SKE in ‘modern’ way o o Definition (Perfect Security: unbounded adversary + no additional leakage) Construction (OTP / Vernam Cipher) Proof Drawbacks (on key length and key reusability) “You should never re-use a one-time pad. It’s like toilet paper; if you re-use it, things get messy. ” Michael Rabin

Today’s Goal - Inherent drawback on key space - More definitions of Perfect Security and their equivalence o Captures different intuition for the same goal o Some definition will be more handy to prove and disprove if a SKE is perfectly -secure o Will further confirm that OTP is optimal in many other ways - Summarizing & Concluding Perfect Security - Find alternative relaxed security notion than perfect security o Introduction to Computational Security > Formulate a formal definition (threat + break model) > Identify assumptions needed and build a construction > Prove security of the construction relative to the definition and assumption

Key Space Must be As Large as the Message Space Theorem: In any perfectly-secure encryption scheme | K | | M | Proof: OTP is optimal key Let c be a ciphertext with Pr(C = c) > 0 length-wise M(c) : = { m | m = Deck (c) for some k} for instance uniformand key Assume the set of all possible decrypted messages distribution overof. Mc(any dist. bility-wise usa Where every message occurs Assume | K | < | M | | M(c) | <|M| with non-zero prob is fine) m M s. t. m M(c) Pr [M = m | C = c] = 0 No perfect Security! Pr [M = m] Show the other limitation is inevitable too!

Perfectly-secure Encryption : Equivalent Definition Perfectly-secure Encryption (Shannon’s Definition): Pr[M = m | C = c] = Pr [M = m] , m M, c C Interpretation : probability of knowing a plain-text remains the same before and after seeing the cipher-text The equivalence holds for any probability distribution over M Perfectly-secure Encryption (Alternate Definition): Pr[C = c | M = m 0] = Pr [C = c | M = m 1], m 0, m 1 M, c C Interpretation : probability distribution of cipher-text is independent of plain-text

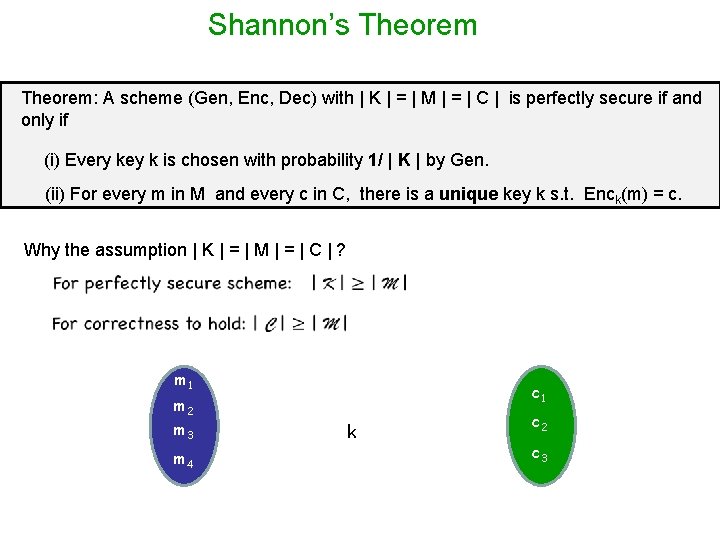
Shannon’s Theorem: A scheme (Gen, Enc, Dec) with | K | = | M | = | C | is perfectly secure if and only if (i) Every key k is chosen with probability 1/ | K | by Gen. (ii) For every m in M and every c in C, there is a unique key k s. t. Enck(m) = c. Why the assumption | K | = | M | = | C | ? m 1 c 1 m 2 m 3 m 4 k c 2 c 3

Shannon’s Theorem: A scheme (Gen, Enc, Dec) with | K | = | M | = | C | is perfectly secure if and only if (i) Every key k is chosen with probability 1/ | K | by Gen. (ii) For every m in M and every c in C, there is a unique key k s. t. Enck(m) = c. Proof: (Part 1) To prove Pr[M = m | C = c] = Pr[M = m] For arbitrary c and m, Pr[C = c | M = m] = Pr[K = k] Pr[C = c] = Σ Pr[C = c | M = m] Pr[M = m] = 1/| K | (irrespective of p. d. over M) m in M = 1/| K | Σ Pr[M = m] = 1/| K | m in M Pr[M = m | C = c] = Pr[C = c | M = m ] Pr[M = m] Pr[C = c] (Bayes' Theorem) = Pr[M = m]

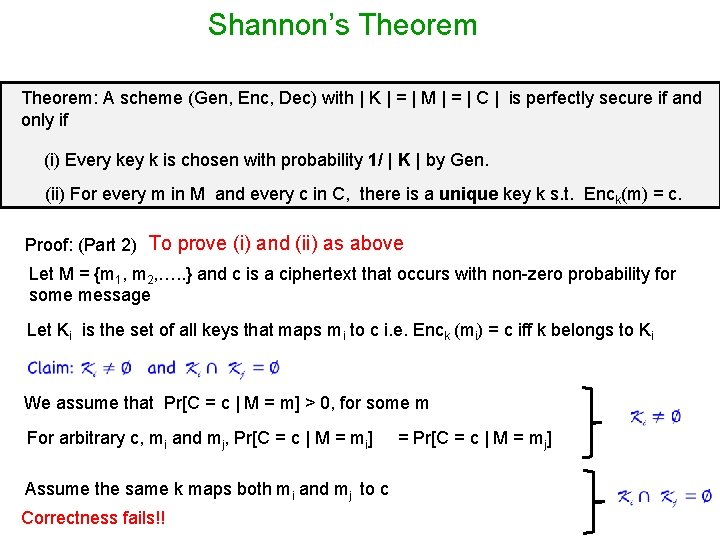
Shannon’s Theorem: A scheme (Gen, Enc, Dec) with | K | = | M | = | C | is perfectly secure if and only if (i) Every key k is chosen with probability 1/ | K | by Gen. (ii) For every m in M and every c in C, there is a unique key k s. t. Enck(m) = c. Proof: (Part 2) To prove (i) and (ii) as above Let M = {m 1, m 2, …. . } and c is a ciphertext that occurs with non-zero probability for some message Let Ki is the set of all keys that maps mi to c i. e. Enck (mi) = c iff k belongs to Ki We assume that Pr[C = c | M = m] > 0, for some m For arbitrary c, mi and mj, Pr[C = c | M = mi] Assume the same k maps both mi and mj to c Correctness fails!! = Pr[C = c | M = mj]

Shannon’s Theorem: A scheme (Gen, Enc, Dec) with | K | = | M | = | C | is perfectly secure if and only if (i) Every key k is chosen with probability 1/ | K | by Gen. (ii) For every m in M and every c in C, there is a unique key k s. t. Enck(m) = c. Proof: (Part 2) To prove (i) and (ii) as above m 1 m 2 mn K 1 K 2 Kn |K|=|M| Pr[K = ki] = | Ki | = 1 Condition (ii) Pr[C = c | M = mi] = Pr[C = c | M = mj] = Pr[K = kj] Condition (i)

Shannon’s Theorem: A scheme (Gen, Enc, Dec) with | K | = | M | = | C | is perfectly secure if and only if (i) Every key k is chosen with probability 1/ | K | by Gen. (ii) For every m in M and every c in C, there is a unique key k s. t. Enck(m) = c. (i) k c e h c o t -Easy and (ii). ny a f o d e e n -No probability ke i l n u n o i t a l calcu ect f r e p l a n i g i or n o i t i n i f e d y t securi

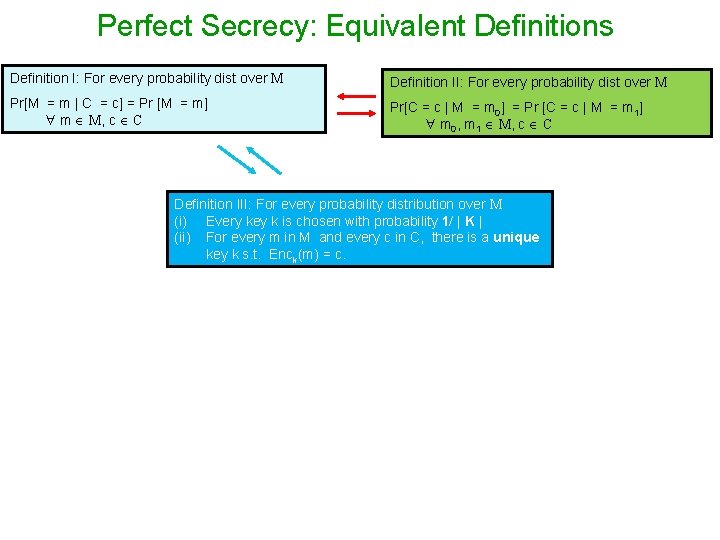
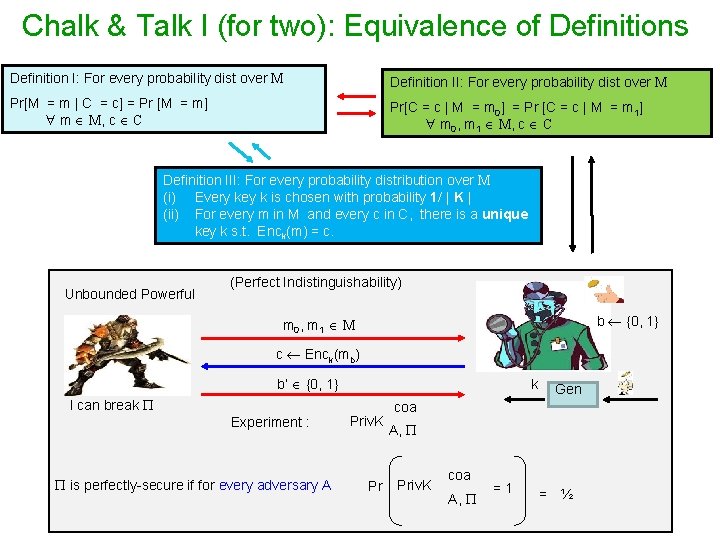
Perfect Secrecy: Equivalent Definitions Definition I: For every probability dist over M Definition II: For every probability dist over M Pr[M = m | C = c] = Pr [M = m] m M, c C Pr[C = c | M = m 0] = Pr [C = c | M = m 1] m 0, m 1 M, c C Definition III: For every probability distribution over M (i) Every key k is chosen with probability 1/ | K | (ii) For every m in M and every c in C, there is a unique key k s. t. Enck(m) = c.

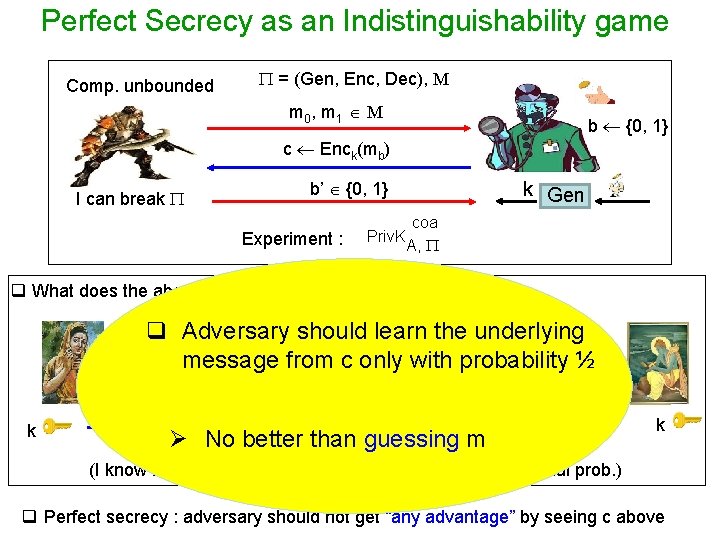
Perfect Secrecy as an Indistinguishability game - Formulated as a challenge-response game between adv. and a verifier = (Gen, Enc, Dec), M Hypothetical verifier Comp. unbounded m 0 , m 1 M (freedom to choose any pair) b {0, 1} c Enck(mb) b’ {0, 1} I can break (Guess about encrypted message) q Game output : Ø 1 if b = b’ Attacker won Ø 0 if b ≠ b’ Attacker lost k Gen

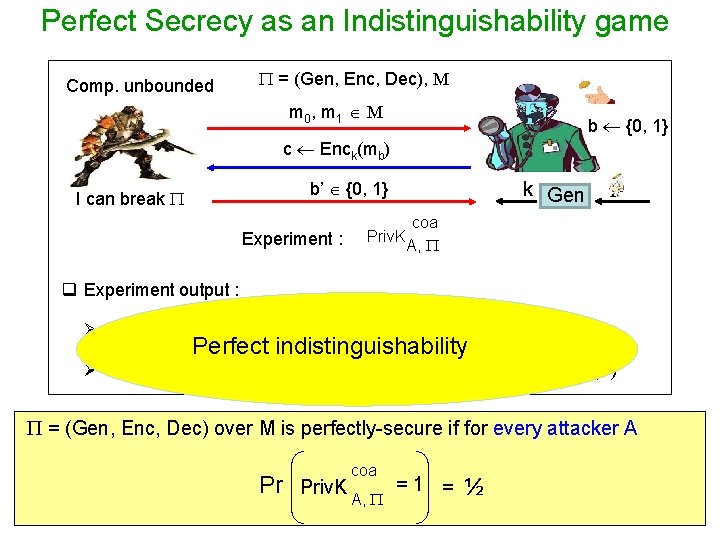
Perfect Secrecy as an Indistinguishability game Comp. unbounded = (Gen, Enc, Dec), M m 0 , m 1 M b {0, 1} c Enck(mb) b’ {0, 1} I can break Experiment : Priv. K k Gen coa A, q What does the above experiment model ? q Adversary should learn the underlying m {m 0, message m 1} from c only with probability ½ c Enc k Ø No better than guessing m k (I know that either m 0 or m 1 will be communicated with equal prob. ) q Perfect secrecy : adversary should not get “any advantage” by seeing c above

Perfect Secrecy as an Indistinguishability game Comp. unbounded = (Gen, Enc, Dec), M m 0 , m 1 M b {0, 1} c Enck(mb) b’ {0, 1} I can break Experiment : Priv. K k Gen coa A, q Experiment output : Ø 1 if b = b’ Attacker won (it found the underlying message) Perfect indistinguishability Ø 0 if b ≠ b’ Attacker lost (failed to find the underlying message) = (Gen, Enc, Dec) over M is perfectly-secure if for every attacker A coa Pr Priv. K A, = 1 = ½

Chalk & Talk I (for two): Equivalence of Definitions Definition I: For every probability dist over M Definition II: For every probability dist over M Pr[M = m | C = c] = Pr [M = m] m M, c C Pr[C = c | M = m 0] = Pr [C = c | M = m 1] m 0, m 1 M, c C Definition III: For every probability distribution over M (i) Every key k is chosen with probability 1/ | K | (ii) For every m in M and every c in C, there is a unique key k s. t. Enck(m) = c. Unbounded Powerful (Perfect Indistinguishability) b {0, 1} m 0, m 1 M c Enck(mb) b’ {0, 1} I can break Experiment : is perfectly-secure if for every adversary A k Priv. K Pr Gen coa A, Priv. K coa A, =1 = ½

Chalk & Talk II (for one) - Implementation of OTP for English text & Cryptanalysis of OTP when key is reused

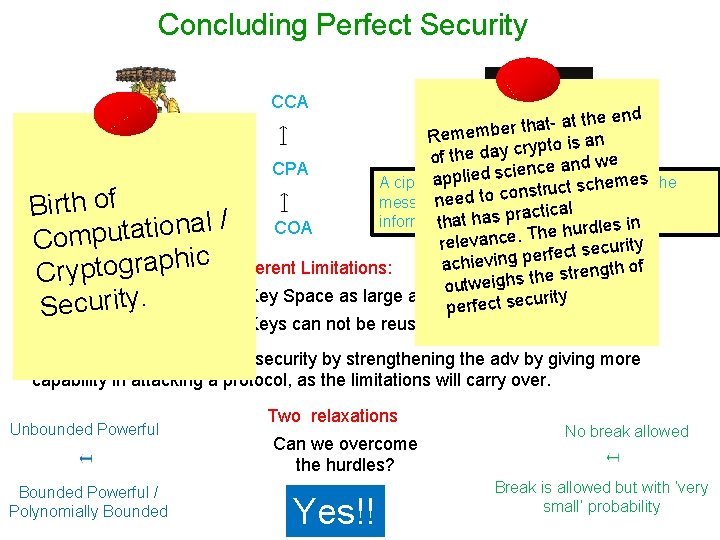
Concluding Perfect Security CCA at the end t a h t r e b Remem to is an p y r c y a d of the nd we a e c CPA n ie c s ed out some info appligives mes the A ciphertext t scheabout Randomized c u r t s n o c to additional to the prior ed is nethat message f o h Unbounded Powerful t r i al B actichas r p s a h t information that the adv a h t COA tional / COA urdles in h e a h t T. u e p c Com relevan ecurity s t c e f r e p c Inherent Limitations: i h p chieving a a r Two g o gth of t n e p r t s e h Cry t utweighs o - Key Space as large as message space. ecurity y s t i t r c e u f r c e p e S - Keys can not be reused No point in studying perfect security by strengthening the adv by giving more capability in attacking a protocol, as the limitations will carry over. Unbounded Powerful Can we overcome the hurdles? Yes!! No break allowed Bounded Powerful / Polynomially Bounded Two relaxations Break is allowed but with ‘very small’ probability

Concluding Perfect Security - Have we put the last nail in the coffin of perfect security? By all means no! - We overlooked efficiently of perfectly-secure scheme among the hullaballoos of limitations! - It’s blazing fast compared to the computationally-secure protocols that we design - Efficiency is in fact hallmark of perfectly-secure schemes - Perfect security is interesting in multi-party setting Many problems in crypto involves more than two parties- MPC, E-election etc. In crypto, we live in the world of trade-offs…

Perfect Security vs. Computational Security Threat is Unbounded Powerful Threat is ‘Computationally Bounded’ No break allowed Break is allowed with ‘small’ probability A scheme is secure if Pr [M = m | C = c] = Pr [M = m] m, c A scheme is secure if any computationally bounded adversary succeeds in ‘breaking’ the scheme with at most ‘some very small probability’. Key as large as the message A small key will do Fresh key for every encryption Key reuse is permitted. Is it necessary to relax the threat and break to overcome the limitations? YES Absolutely!