Cryptography Lecture 5 Arpita Patra Arpita Patra Recall

Cryptography Lecture 5 Arpita Patra © Arpita Patra

Recall >> Computational Security o Made PPT/negligible function precise in terms of security parameter n o Semantic and Indistinguishability Security notions o Ind-based definitions are easy to follow o Assumptions needed for a scheme o Pseudorandomness

Today’s Goal - Pseudorandomness and PRGs - Construction for ind-secure scheme - Proof: If there is a PRG, then the construction is secure according to ind definition o Introduction to Reduction-based proofs o Proof for our construction - Short-comings of the current construction/definition - Better definition / better construction / better assumption?

Pseudorandomness - It’s a property of a probability distribution { Set of all binary strings of length l } U: Uniform probability Distribution G: a prob. Dist. = { Set of probabilities } Sampler for G and U Give me a string A string drawn according to G is called pseudorandom A string drawn according to U is called random w G is pseudorandom if a string drawn according to G is indistinguishable from a string drawn according to U to a PPT distinguisher

Pseudorandom Generators (PRGs) Deterministic PPT Algorithm G s R {0, 1}n G(s) {0, 1}l(n) , l: poly Seed Let G be the dist. on l(n)-bit strings obtained by sampling s uniformly and running G(s). G is a PRG if dist. G is pseudorandom distribution and l(n) > n for every n. l() : expansion factor of G Requirements : 1. Expansion : for every n, l(n) > n 2. Pseudorandomness : G(s) “looks like” a truly random string

PRG Security Oracle U : uniform distribution over {0, 1}l(n) PPT distinguisher D A string of length l(n) please y How I selected it ? of g Challenger lz in str n) p om th l( d ) l(n ran leng A 1} , 0 { b= 0 R y b= 1 s R G: Probability distribution over {G(s): s R {0, 1}n} G is a PRG if for every PPT D, there is a negligible function negl | Pr [D(r) = 1] - Pr [D(G(s)) = 1] | negl(n) n r {0, 1}l(n) R s R {0, 1} Probability taken over >> Random Choice of s >> the randomness of D y: = {0, 1} n G( s) G

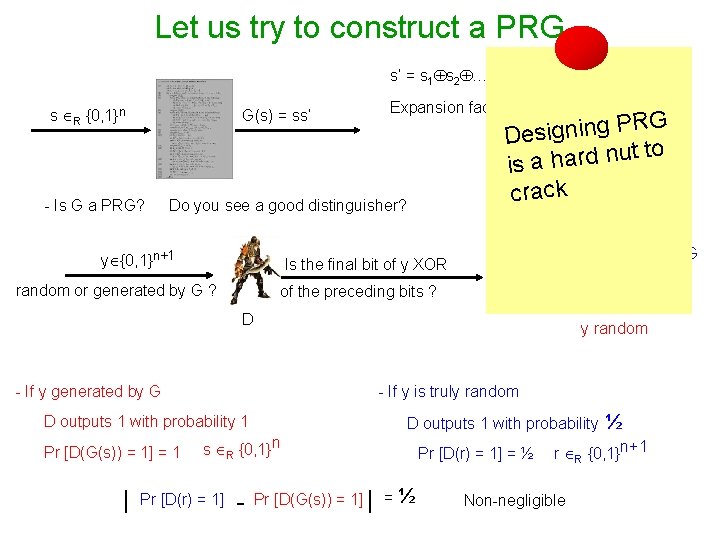
Let us try to construct a PRG… s’ = s 1 s 2 … sn s R {0, 1}n G(s) = ss’ - Is G a PRG? Expansion factor: n+1 PRG g n i n g i s e D t to u n d r a h a is crack Do you see a good distinguisher? D outputs 1 s y {0, 1}n+1 Is the final bit of y XOR random or generated by G ? of the preceding bits ? Ye y generated by G No D outputs 0 D - If y generated by G - If y is truly random D outputs 1 with probability 1 Pr [D(G(s)) = 1] = 1 | y random D outputs 1 with probability s R {0, 1}n Pr [D(r) = 1] - Pr [D(G(s)) = 1] | = ½ Pr [D(r) = 1] = ½ ½ r R {0, 1}n+1 Non-negligible

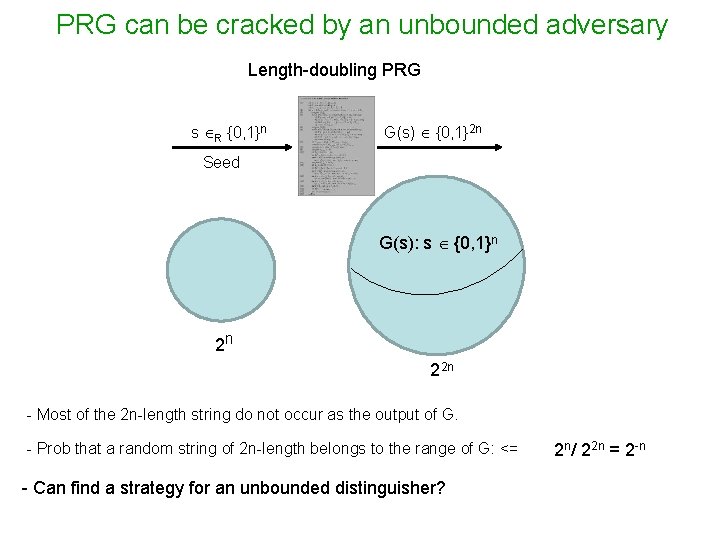
PRG can be cracked by an unbounded adversary Length-doubling PRG s R {0, 1}n G(s) {0, 1}2 n Seed G(s): s {0, 1}n 2 n 22 n - Most of the 2 n-length string do not occur as the output of G. - Prob that a random string of 2 n-length belongs to the range of G: <= - Can find a strategy for an unbounded distinguisher? 2 n/ 22 n = 2 -n

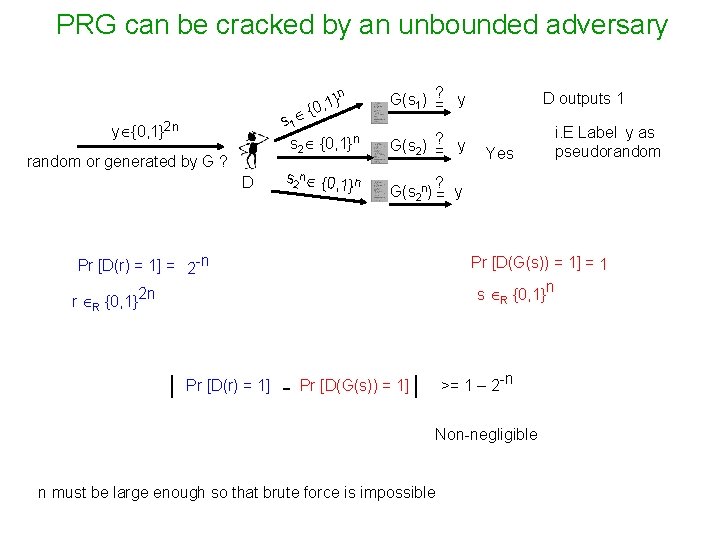
PRG can be cracked by an unbounded adversary n } 0, 1 { s 1 s 2 {0, 1}n y {0, 1}2 n random or generated by G ? D s 2 n {0, 1} n G(s 1) ? = y G(s 2) ? = y D outputs 1 Yes ? G(s 2 n) = y Pr [D(r) = 1] = 2 -n Pr [D(G(s)) = 1] = 1 s R {0, 1}n r R {0, 1}2 n | Pr [D(r) = 1] i. E Label y as pseudorandom - >= 1 – 2 -n Pr [D(G(s)) = 1] | Non-negligible n must be large enough so that brute force is impossible

Do PRGs exist? No proof… But we strongly believe they do Didn’t we just say we believe something is true but don’t have a proof? First Assumption in the course: PRGs exist. Later in the course………. PRGs exist ao Y , in ev dr ol -L h c i e G One-way functions (permutation) exist Far from practical Be ca us en og oo dd ist ing uis he r Stream Ciphers Highly practical RA 4: Define Stream Ciphers and describe Trivium

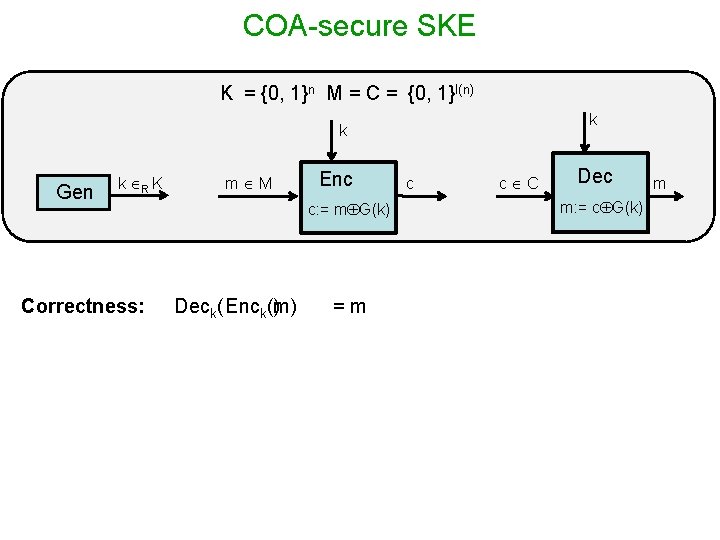
COA-secure SKE K = {0, 1}n M = C = {0, 1}l(n) k k Gen k R K Correctness: m M Enc c: = m G(k) Deck( Enck(m) ) =m c c C Dec m: = c G(k) m

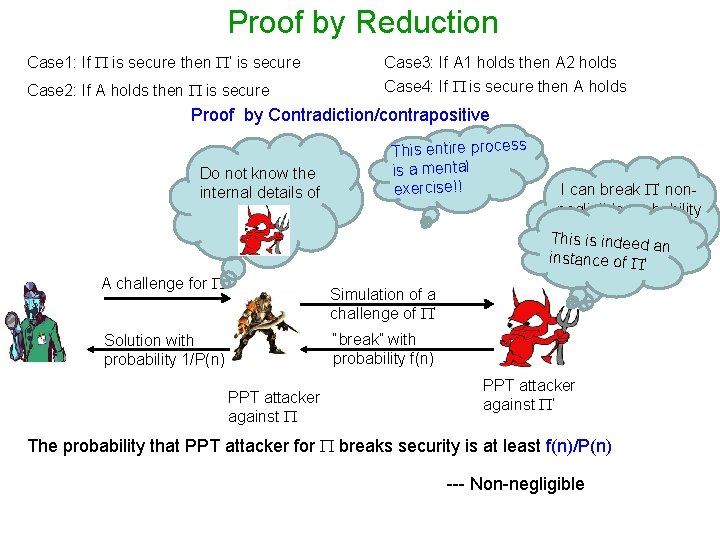
Proof by Reduction Case 1: If is secure then ’ is secure Case 3: If A 1 holds then A 2 holds Case 2: If A holds then is secure Case 4: If is secure then A holds Proof by Contradiction/contrapositive Do not know the internal details of A challenge for This entire process is a mental exercise!! I can break ’ nonnegligible probability f(n) This is indeed a n instance of ’ Simulation of a challenge of ’ “break” with probability f(n) Solution with probability 1/P(n) PPT attacker against ’ The probability that PPT attacker for breaks security is at least f(n)/P(n) --- Non-negligible

Indistinguishability Based Definition: COA Priv. K Indistinguishability experiment coa A, (n) = (Gen, Enc, Dec), M Attacker A Challenger , 1} {0 b m 0, m 1 M ; |m 0|=|m 1| (freedom to choose any pair) I can break Run time: Poly(n) b’ {0, 1} (Attacker’s guess about encrypted message) ’ b=b Priv. K 1 --- attacker won coa A, (n) b b ’ Let me verify k c Enck(mb) Gen(1 n) 0 --- attacker lost All Security Definitions will be in Ind style has is coa-secure if for every PPT attacker A, there is a negligible function negl(n) such that SEM Security ≈ IND Security coa Pr Priv. K (n) = 1 A, ½ + negl(n) Probability is taken over the randomness used by A and the challenger

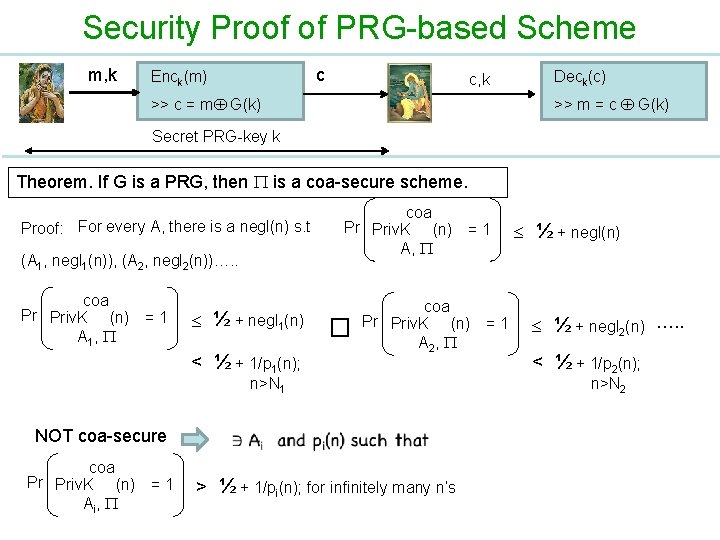
Security Proof of PRG-based Scheme m, k c Enck(m) c, k Deck(c) >> m = c G(k) >> c = m G(k) Secret PRG-key k Theorem. If G is a PRG, then is a coa-secure scheme. Proof: For every A, there is a negl(n) s. t (A 1, negl 1(n)), (A 2, negl 2(n))…. . coa Pr Priv. K (n) = 1 A 1, ½ + negl 1(n) < ½ + 1/p 1(n); coa Pr Priv. K (n) = 1 A, � coa Pr Priv. K (n) = 1 A 2, n>N 1 NOT coa-secure coa Pr Priv. K (n) = 1 Ai , > ½ + 1/pi(n); for infinitely many n’s ½ + negl(n) ½ + negl 2(n) …. . < ½ + 1/p 2(n); n>N 2

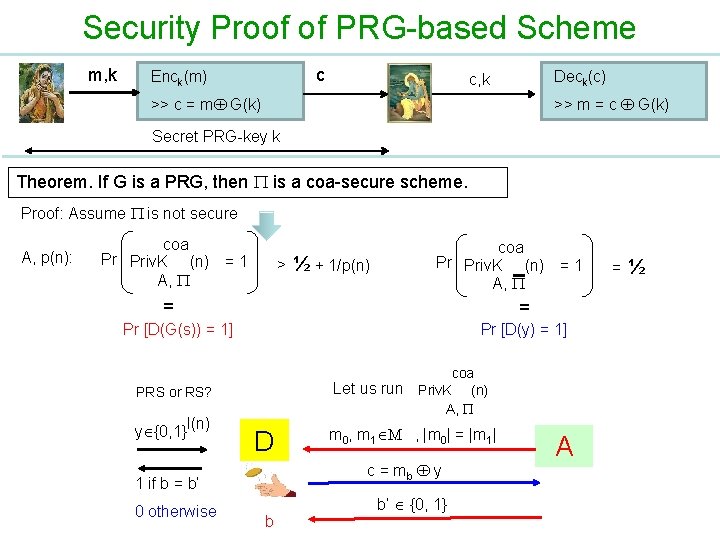
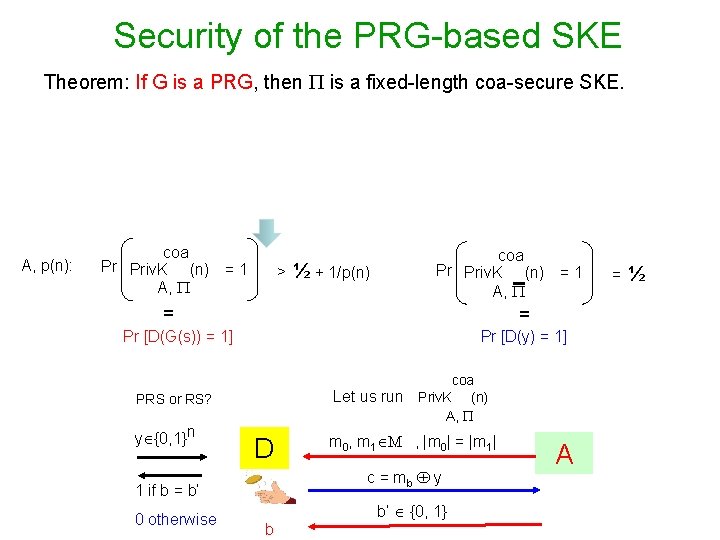
Security Proof of PRG-based Scheme m, k c Enck(m) Deck(c) c, k >> m = c G(k) >> c = m G(k) Secret PRG-key k Theorem. If G is a PRG, then is a coa-secure scheme. Proof: Assume is not secure A, p(n): coa Pr Priv. K (n) = 1 A, > ½ + 1/p(n) coa Pr Priv. K (n) = 1 A, = = Pr [D(G(s)) = 1] Pr [D(y) = 1] coa Let us run Priv. K (n) A, PRS or RS? y {0, 1}l(n) D c = mb y 1 if b = b’ 0 otherwise m 0, m 1 M , |m 0| = |m 1| b b’ {0, 1} A = ½

What have we done so far. . o Formulate a formal definition for SKE in computational world o Identify assumptions needed (PRG exists) and build a construction o Prove security of the construction relative to the definition and assumption o Small Key size. o Key Reuse? ? Let us formalize key reuse in the definition and see if the schemes we have seen satisfy the definition

Multiple-message COA Security coa-mult Priv. K (n) A, Attacker A = (Gen, Enc, Dec), M M 0 = (m 0, 1, …, m 0, t) M 1 = (m 1, 1, …, m 1, t) {0 b , 1} (freedom to choose any pair) I can break Run time: Poly(n) b’ {0, 1} Let me verify (Attacker’s guess about encrypted vector) ’ b=b Game Output 1 --- attacker won b b ’ k c 1 Enck(mb, 1) , …, ct Enck(mb, t) Gen(1 n) 0 --- attacker lost is coa-mult-secure if for every PPT attacker A taking part in the above experiment, the probability that A wins the experiment is at most negligibly better than ½ coa-mult i. e. Pr Priv. K (n) = 1 A, ½ + negl(n)

Relation between Multiple-message and Singlemessage Security q Experiment Ø coa Priv. K (n) is A, coa Priv. K (n) is a A, special case of the same as coa-mult Priv. K with (n) |M 0| A, coa-mult Priv. K (n) A, = |M 1| = 1 q Any cipher which is coa-mult-secure is also coa-secure q What about the converse ? Ø Not necessarily

Multiple-message Security is Stronger than Single-message Security coa-mult Pr Priv. K (n) = 1 A, OTP q c 1 : = hello k c 2 : = hello k If b = 0 c 1 : = hello k c 2 : = world k If b = 1 =1 b’ = 0 if c 1 = c 2 b Let me verify b’ = 1 if c 1 c 2 } , 1 {0 k M 0 = (hello, hello) M 0 = (hello, world) Attacker A Gen(1 n) Why the above attack is possible ? Ø OTP is deterministic: encrypting m twice using same key yields the same ciphertext Ø The above attack can be mounted on any cipher whose Enc algorithm is deterministic Thm: If is a cipher whose Enc algorithm is a deterministic function of the key and the plaintext then cannot have indistinguishable multiple encryptions in the presence of an eavesdropper Time to Go for Randomization of Encryption

What next? q coa is not standard; have done for gradual progress. q Will give an even stronger definition and construct a scheme. That will be secure according to coa and coa-mult.

Two assumptions and Their Implications Two assumptions: o PRGs exist o coa-secure SKEs exist. Do they imply something fundamental exist?

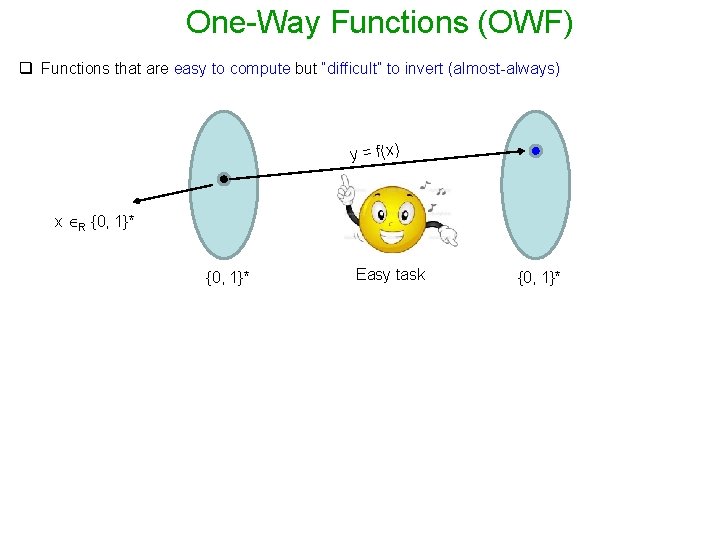
One-Way Functions (OWF) q Functions that are easy to compute but “difficult” to invert (almost-always) f: {0, 1}*

One-Way Functions (OWF) q Functions that are easy to compute but “difficult” to invert (almost-always) y = f(x) x R {0, 1}* Easy task {0, 1}*

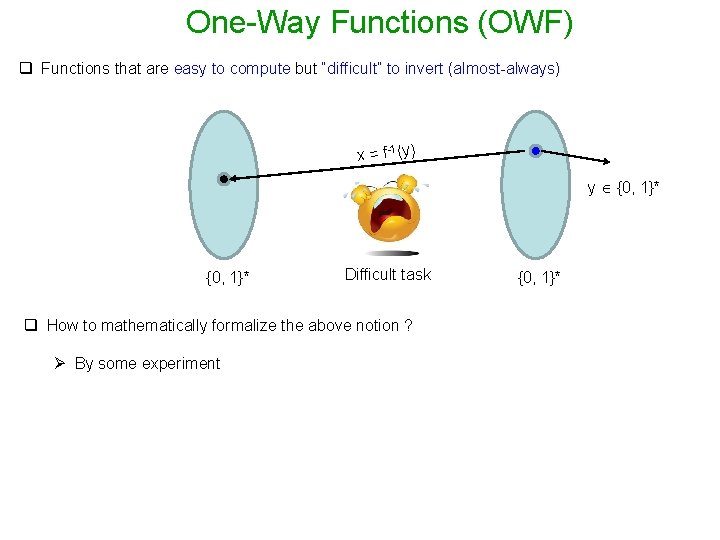
One-Way Functions (OWF) q Functions that are easy to compute but “difficult” to invert (almost-always) x = f-1 (y) y {0, 1}* Difficult task q How to mathematically formalize the above notion ? Ø By some experiment {0, 1}*

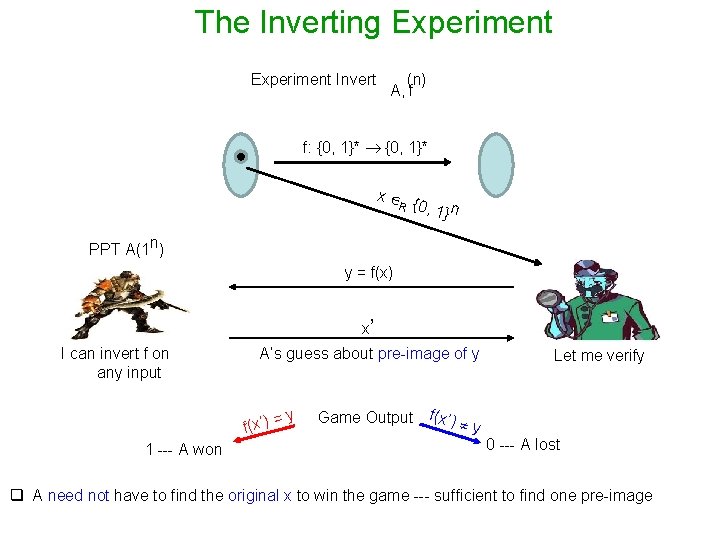
The Inverting Experiment Invert (n) A, f f: {0, 1}* x R {0, 1 n } PPT A(1 n) y = f(x) x’ I can invert f on any input A’s guess about pre-image of y f(x’) = 1 --- A won y Game Output f(x’) y Let me verify 0 --- A lost q A need not have to find the original x to win the game --- sufficient to find one pre-image

OWF: Mathematical Formulation f: {0, 1}* q Function f is a OWF if the following two conditions hold : Ø Easy to compute: for every x {0, 1}*, f(x) can be computed in poly(n) times Ø Hard to Invert: For every PPT algorithm A, there is a negligible function negl() : Pr Invert (n) A, f = 1 negl(n) Pr x {0, 1}n [ A(f(x), 1 n) f-1(f(x))] negl(n)

Two assumptions and Their Implications CT 5 (for one): If PRG exists then OWF exists CT 6 (for one): If coa-secure SKE exists, then OWF exists.

Scribe?

Security of the PRG-based SKE Theorem: If G is a PRG, then is a fixed-length coa-secure SKE. A, p(n): coa Pr Priv. K (n) = 1 A, > ½ + 1/p(n) coa Pr Priv. K (n) = 1 A, = = Pr [D(G(s)) = 1] Pr [D(y) = 1] coa Let us run Priv. K (n) A, PRS or RS? y {0, 1}n D c = mb y 1 if b = b’ 0 otherwise m 0, m 1 M , |m 0| = |m 1| b b’ {0, 1} A = ½