Foundations of Secure Computation Arpita Patra Arpita Patra

Foundations of Secure Computation Arpita Patra © Arpita Patra

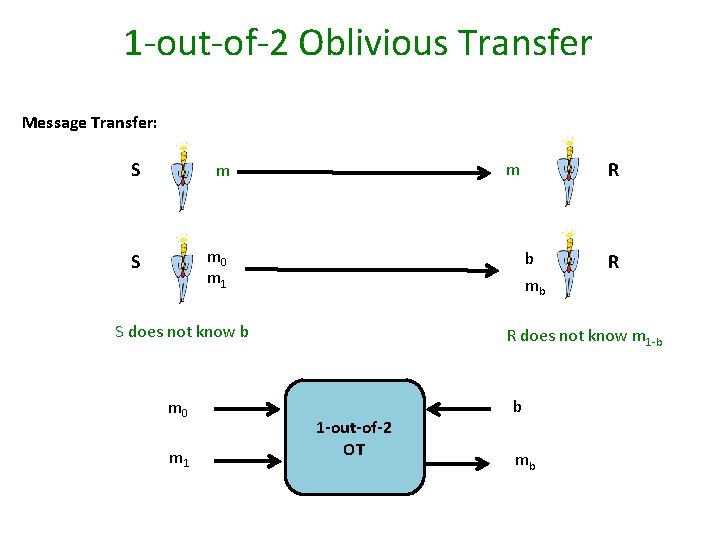
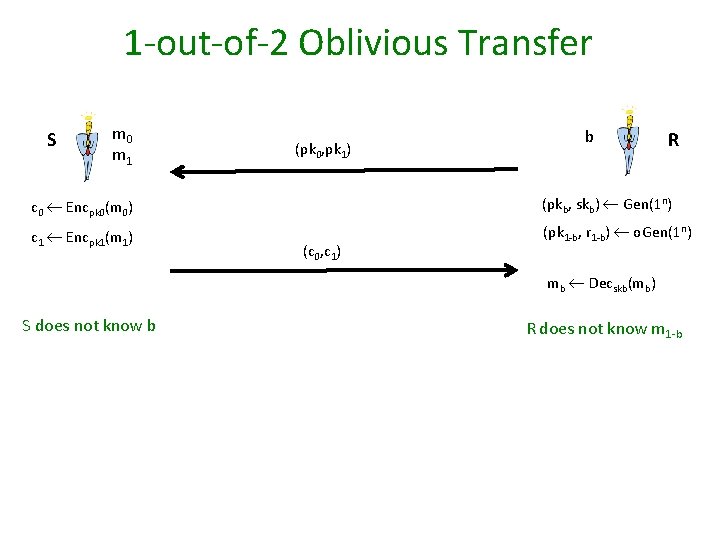
1 -out-of-2 Oblivious Transfer Message Transfer: S m 0 m 1 b mb S does not know b m 0 m 1 R m R R does not know m 1 -b 1 -out-of-2 OT b mb

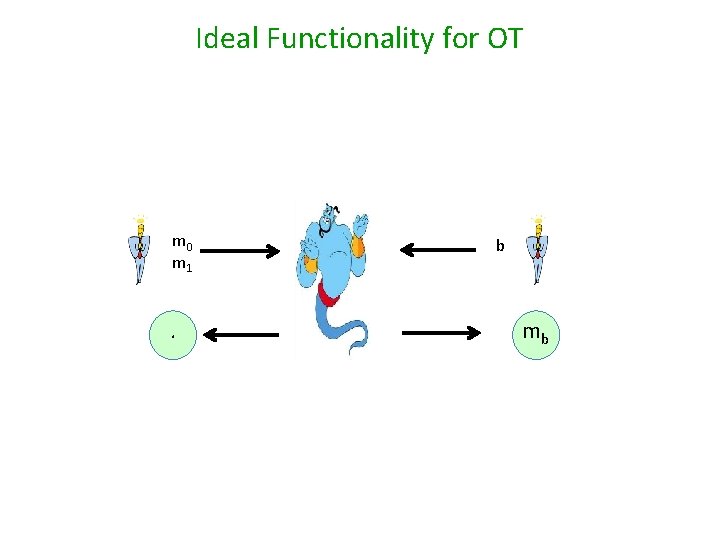
Ideal Functionality for OT m 0 m 1 . b mb

OT from CPA-secure PKE with Public Key Samplability [Even. Goldreich. Lempel 85] >> A public-key encryption scheme is a collection of 3 PPT algorithms = (Gen, Enc, Dec) 1 n pk, sk {0, 1}n Gen Syntax: (pk, sk) Gen(1 n) Randomized Algo pk m M c Enc Randomized algo sk c Dec Syntax: c Encpk(m) Syntax: m: = Decsk(c) m Deterministic (w. l. o. g) Except with a negligible probability over (pk, sk) output by Gen(1 n), we require the following for every (legal) plaintext m Decsk(Encpk(m)): = m

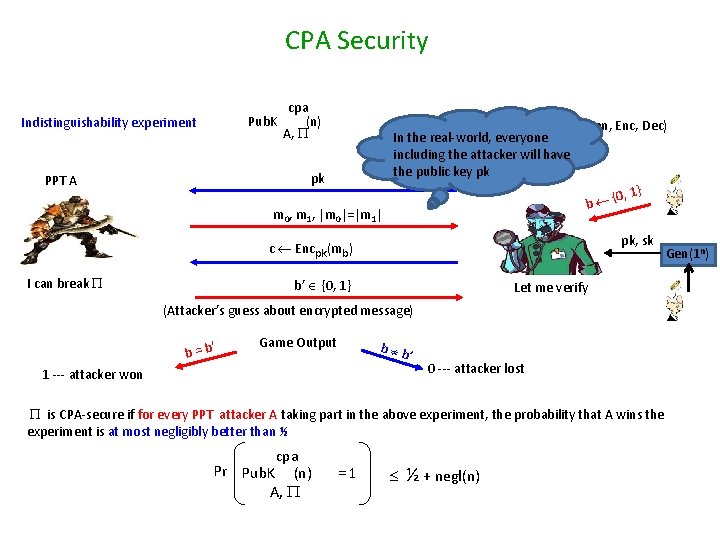
CPA Security cpa Pub. K (n) A, Indistinguishability experiment pk PPT A m 0, m 1, |m 0|=|m 1| = (Gen, Enc, Dec) In the real-world, everyone including the attacker will have the public key pk {0, 1} b pk, sk c Encpk(mb) I can break b’ {0, 1} Let me verify (Attacker’s guess about encrypted message) ’ b=b Game Output b b ’ 1 --- attacker won 0 --- attacker lost is CPA-secure if for every PPT attacker A taking part in the above experiment, the probability that A wins the experiment is at most negligibly better than ½ cpa Pr Pub. K (n) A, =1 ½ + negl(n) Gen(1 n)

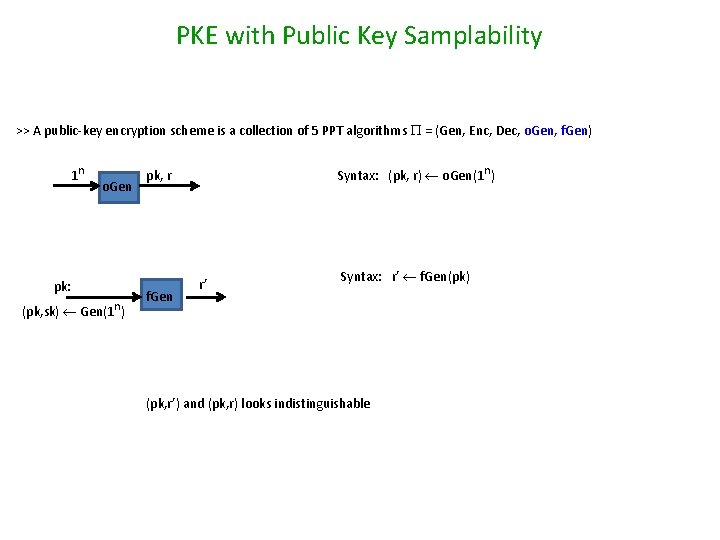
PKE with Public Key Samplability >> A public-key encryption scheme is a collection of 5 PPT algorithms = (Gen, Enc, Dec, o. Gen, f. Gen) 1 n o. Gen pk: (pk, sk) Gen(1 n) Syntax: (pk, r) o. Gen(1 n) pk, r f. Gen r’ Syntax: r’ f. Gen(pk) (pk, r’) and (pk, r) looks indistinguishable

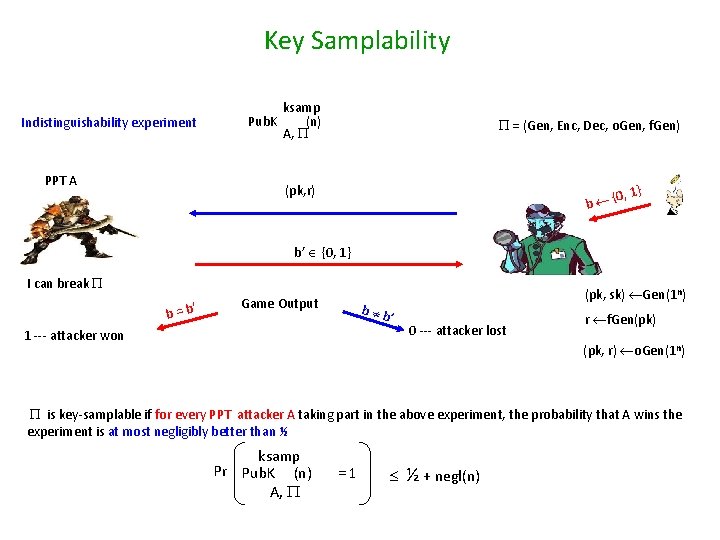
Key Samplability Indistinguishability experiment PPT A ksamp Pub. K (n) A, = (Gen, Enc, Dec, o. Gen, f. Gen) (pk, r) {0, 1} b b’ {0, 1} I can break ’ b=b Game Output b b ’ 1 --- attacker won (pk, sk) Gen(1 n) 0 --- attacker lost r f. Gen(pk) (pk, r) o. Gen(1 n) is key-samplable if for every PPT attacker A taking part in the above experiment, the probability that A wins the experiment is at most negligibly better than ½ ksamp Pr Pub. K (n) A, =1 ½ + negl(n)

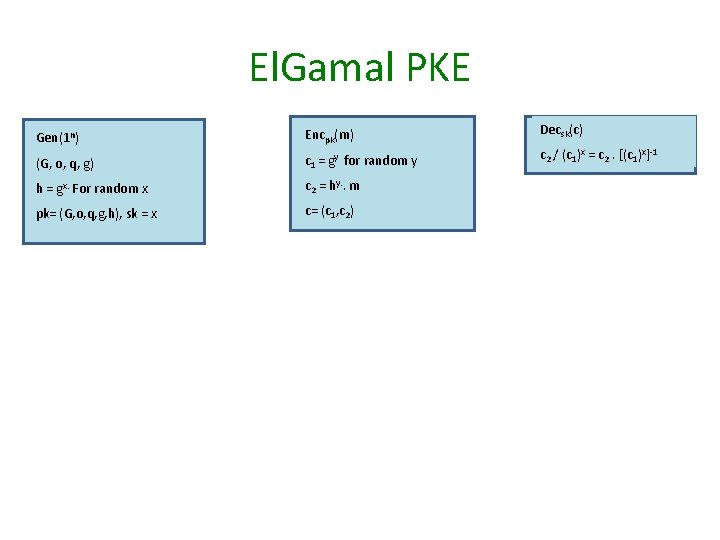
El. Gamal PKE Gen(1 n) Encpk(m) Decsk(c) (G, o, q, g) c 1 = gy for random y c 2 / (c 1)x = c 2. [(c 1)x]-1 h = gx. For random x c 2 = hy. . m pk= (G, o, q, g, h), sk = x c= (c 1, c 2)

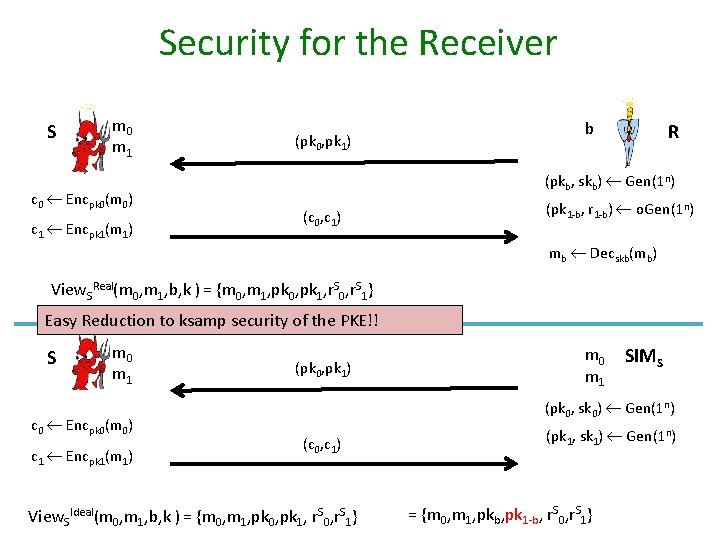
1 -out-of-2 Oblivious Transfer S m 0 m 1 (pk 0, pk 1) b R c 0 Encpk 0(m 0) (pkb, skb) Gen(1 n) c 1 Encpk 1(m 1) (pk 1 -b, r 1 -b) o. Gen(1 n) (c 0, c 1) mb Decskb(mb) S does not know b R does not know m 1 -b

Security for the Receiver S m 0 m 1 c 0 Encpk 0(m 0) c 1 Encpk 1(m 1) (pk 0, pk 1) b R (pkb, skb) Gen(1 n) (c 0, c 1) (pk 1 -b, r 1 -b) o. Gen(1 n) mb Decskb(mb) View. SReal(m 0, m 1, b, k ) = {m 0, m 1, pk 0, pk 1, r. S 0, r. S 1} Easy Reduction to ksamp security of the PKE!! S m 0 m 1 c 0 Encpk 0(m 0) c 1 Encpk 1(m 1) (pk 0, pk 1) m 0 m 1 SIMS (pk 0, sk 0) Gen(1 n) (c 0, c 1) View. SIdeal(m 0, m 1, b, k ) = {m 0, m 1, pk 0, pk 1, r. S 0, r. S 1} (pk 1, sk 1) Gen(1 n) = {m 0, m 1, pkb, pk 1 -b, r. S 0, r. S 1}

Indistinguishability of Real and Ideal View Theorem. If is ksamp-secure, then our OT provides receiver security according to real world/ideal world paradigm. Proof: Assume OT does not provide receiver security D, p(n): Pr D(View. SReal(m 0, m 1, b, k) =1) - D(View. SIdeal(m 0, m 1, b, k) =1) {m 0, m 1, pkb, pk 1 -b, r. S 0, r. S 1} A (pk, r) by o. Gen or (Gen, f. Gen) (pk, r) b’ {0, 1} m 0, m 1 (pkb, skb) Gen(1 n) > ½ + 1/p(n) {m 0, m 1, pkb, pk 1 -b, r. S 0, r. S 1} m 0, m 1, pk 0, pk 1, r. S 0, r. S 1 D b’ {0, 1} pk 1 -b = pk r. S 0, r. S 1 If b is guessed correctly, then A emulates Real/Idea View -> A breaks ksamp security with non-negligible advantage (PKE is not ksamp-secure) -> Contradiction

Security for the Sender S m 0 m 1 c 0 Encpk 0(m 0) c 1 Encpk 1(m 1) (pk 0, pk 1) b R (pkb, skb) Gen(1 n) (c 0, c 1) (pk 1 -b, r 1 -b) o. Gen(1 n) mb Decskb(mb) View. RReal(m 0, m 1, b, k ) = {b, mb, pkb, rb, pk 1 -b, r 1 -b , c 0, c 1} Reduction to CPA does not work as c 1 -b is encrypted using a public key generated by b Gen o. Gen NOT SIM b (pk 0, pk 1) R mb cb Encpkb(mb) c 1 -b Encpk 1 -b(0 k) R (pkb, skb) Gen(1 n) (c 0, c 1) (pk 1 -b, r 1 -b) o. Gen(1 n) mb Decskb(mb) View. RIdeal(m 0, m 1, b, k ) = {b, mb, pkb, rb, pk 1 -b, r 1 -b , cb, c 1 -b}

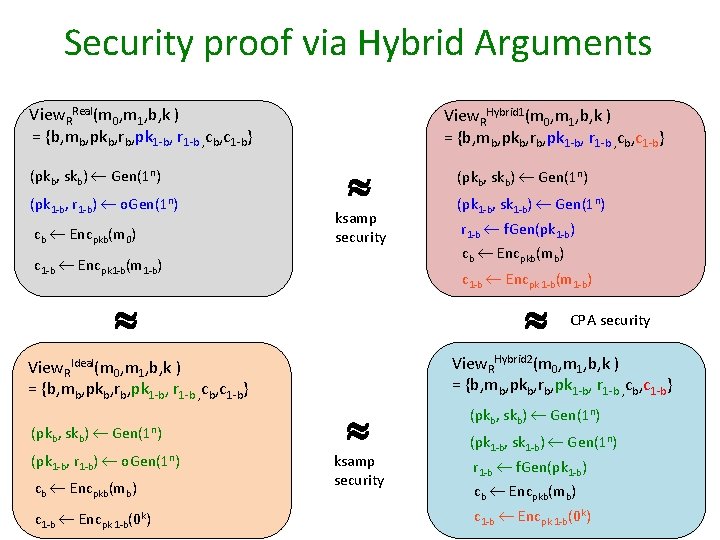
Security proof via Hybrid Arguments View. RReal(m 0, m 1, b, k ) = {b, mb, pkb, rb, pk 1 -b, r 1 -b , cb, c 1 -b} (pkb, skb) Gen(1 n) (pk 1 -b, r 1 -b) o. Gen(1 n) cb Encpkb(m 0) View. RHybrid 1(m 0, m 1, b, k ) = {b, mb, pkb, rb, pk 1 -b, r 1 -b , cb, c 1 -b} ksamp security c 1 -b Encpk 1 -b(m 1 -b) (pkb, skb) Gen(1 n) (pk 1 -b, r 1 -b) o. Gen(1 n) cb Encpkb(mb) c 1 -b Encpk 1 -b(0 k) (pk 1 -b, sk 1 -b) Gen(1 n) r 1 -b f. Gen(pk 1 -b) cb Encpkb(mb) c 1 -b Encpk 1 -b(m 1 -b) View. RIdeal(m 0, m 1, b, k ) = {b, mb, pkb, rb, pk 1 -b, r 1 -b , cb, c 1 -b} (pkb, skb) Gen(1 n) CPA security View. RHybrid 2(m 0, m 1, b, k ) = {b, mb, pkb, rb, pk 1 -b, r 1 -b , cb, c 1 -b} (pkb, skb) Gen(1 n) ksamp security r 1 -b f. Gen(pk 1 -b) cb Encpkb(mb) (pk 1 -b, sk 1 -b) Gen(1 n) c 1 -b Encpk 1 -b(0 k)

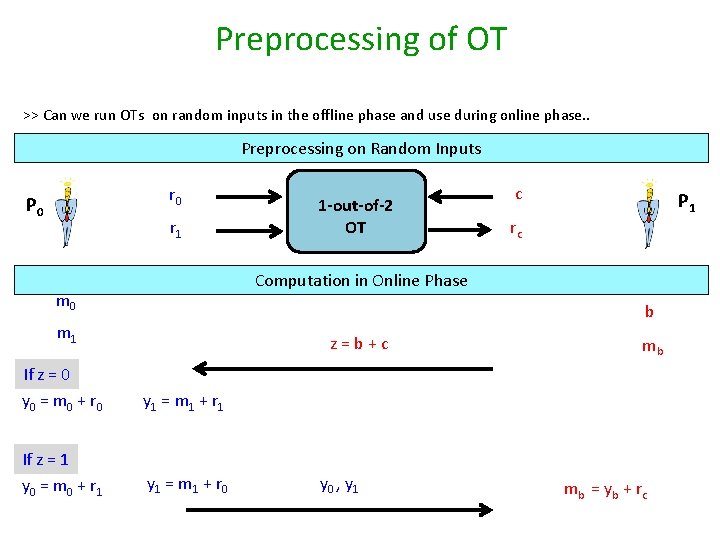
Preprocessing of OT >> Can we run OTs on random inputs in the offline phase and use during online phase. . Preprocessing on Random Inputs r 0 P 0 r 1 1 -out-of-2 OT c P 1 rc Computation in Online Phase m 0 b m 1 z=b+c If z = 0 y 0 = m 0 + r 0 y 1 = m 1 + r 1 If z = 1 y 0 = m 0 + r 1 y 1 = m 1 + r 0 y 0 , y 1 mb mb = yb + rc

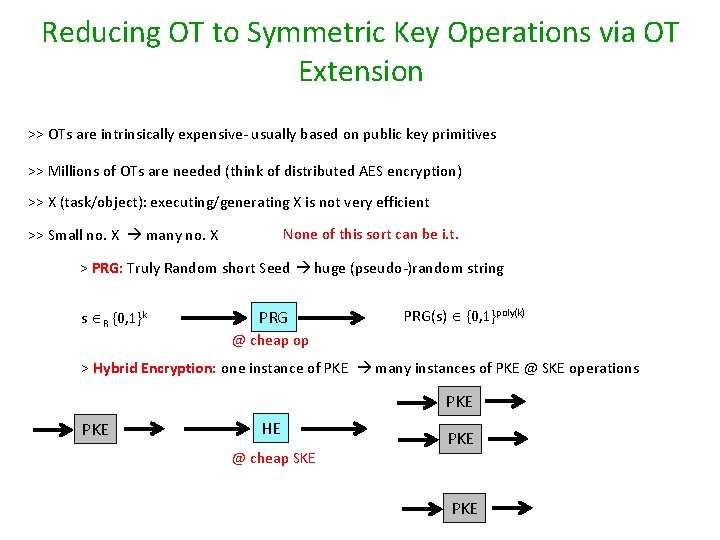
Reducing OT to Symmetric Key Operations via OT Extension >> OTs are intrinsically expensive- usually based on public key primitives >> Millions of OTs are needed (think of distributed AES encryption) >> X (task/object): executing/generating X is not very efficient None of this sort can be i. t. >> Small no. X many no. X > PRG: Truly Random short Seed huge (pseudo-)random string s R {0, 1}k PRG(s) {0, 1}poly(k) @ cheap op > Hybrid Encryption: one instance of PKE many instances of PKE @ SKE operations PKE HE @ cheap SKE PKE

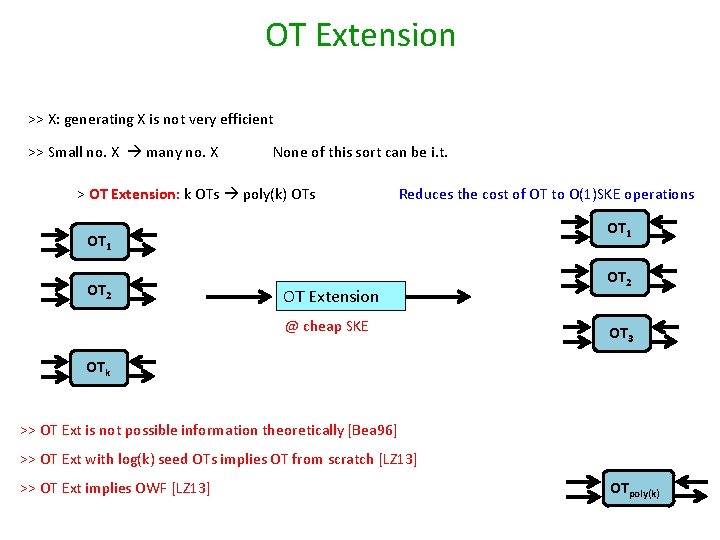
OT Extension >> X: generating X is not very efficient >> Small no. X many no. X None of this sort can be i. t. > OT Extension: k OTs poly(k) OTs Reduces the cost of OT to O(1)SKE operations OT 1 OT 2 OT Extension @ cheap SKE OT 2 OT 3 OTk >> OT Ext is not possible information theoretically [Bea 96] >> OT Ext with log(k) seed OTs implies OT from scratch [LZ 13] >> OT Ext implies OWF [LZ 13] OTpoly(k)

Roadmap for Building OT Extension [IKNP 03] k bit inputs l bit inputs m (=poly(k)) > k bit inputs OT 1 OT 2 OTk Cost for transformation r 10 r 11 r 20 r 21 r 30 r 31 OT 1 b 1 r 1 b 1 OT 2 b 2 r 2 b 2 OT 3 b 3 r 3 b 3 OTm bm rm bm Cost for transformation rm 0 rm 1

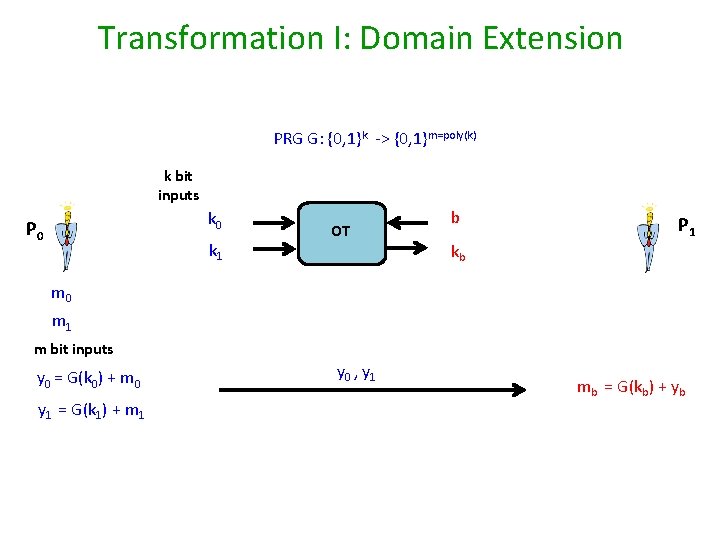
Transformation I: Domain Extension PRG G: {0, 1}k -> {0, 1}m=poly(k) k bit inputs k 0 P 0 k 1 OT b kb P 1 m 0 m 1 m bit inputs y 0 = G(k 0) + m 0 y 1 = G(k 1) + m 1 y 0 , y 1 mb = G(kb) + yb

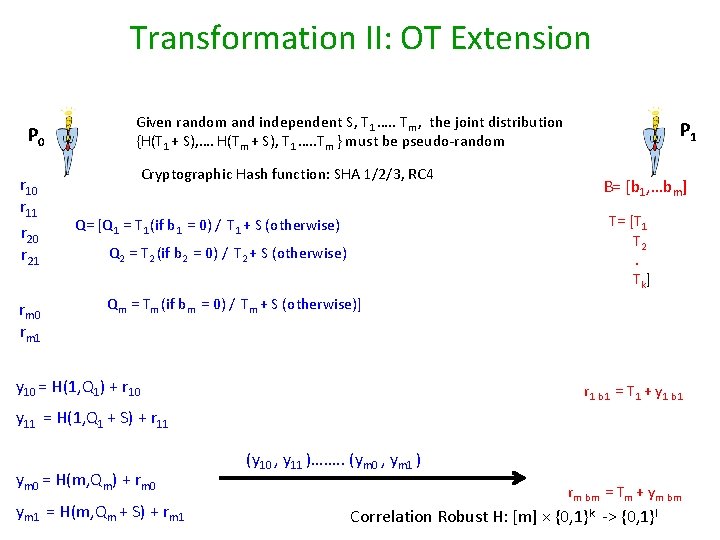
Transformation II: OT Extension P 1 P 0 r 11 B= [b 1, …bm] r 1 b 1 r 20 r 21 r 2 b 2 rm 0 rm 1 rm bm Q= [Q 1 = T 1 (if b 1 = 0) / T 1 + S (otherwise) Q 2 = T 2 (if b 2 = 0) / T 2 + S (otherwise) T= [T 1 T 2. Tm] Qm = Tm (if bm = 0) / Tm + S (otherwise)] Random S is known to P 0 only |Ti| = k

Transformation II: OT Extension There’s a Big Bug! P 0 r 11 r 20 r 21 P 1 B= [b 1, …bm] Q= [Q 1 = T 1 (if b 1 = 0) / T 1 + S (otherwise) rm 0 rm 1 Q 2 = T 2 (if b 2 = 0) / T 2 + S (otherwise) T= [T 1 T 2. Tm] Qm = Tm (if bm = 0) / Tm + S (otherwise)] y 10 = Q 1 + r 10 r 1 b 1 = T 1 + y 1 b 1 y 11 = Q 1 + S + r 11 ym 0 = Qm + rm 0 ym 1 = Qm + S + rm 1 (y 10 , y 11 )……. . (ym 0 , ym 1 ) rm bm = Tm + ym bm

Transformation II: OT Extension P 0 r 11 r 20 r 21 rm 0 rm 1 Given random and independent S, T 1 …. . Tm , the joint distribution {H(T 1 + S), …. H(Tm + S), T 1 …. . Tm } must be pseudo-random Cryptographic Hash function: SHA 1/2/3, RC 4 P 1 B= [b 1, …bm] T= [T 1 T 2. Tk] Q= [Q 1 = T 1 (if b 1 = 0) / T 1 + S (otherwise) Q 2 = T 2 (if b 2 = 0) / T 2 + S (otherwise) Qm = Tm (if bm = 0) / Tm + S (otherwise)] y 10 = H(1, Q 1) + r 10 r 1 b 1 = T 1 + y 1 b 1 y 11 = H(1, Q 1 + S) + r 11 ym 0 = H(m, Qm) + rm 0 ym 1 = H(m, Qm + S) + rm 1 (y 10 , y 11 )……. . (ym 0 , ym 1 ) rm bm = Tm + ym bm Correlation Robust H: [m] × {0, 1}k -> {0, 1}l

Transformation II: OT Extension P 1 P 0 r 11 r 20 r 21 rm 0 rm 1 Every time query an input: same output New input: output is completely random in the range Every RO is Correlation-Robust (HR) Hash function B= [b 1, …bm] T= [T 1 T 2. Tk] Q= [Q 1 = T 1 (if b 1 = 0) / T 1 + S (otherwise) Q 2 = T 2 (if b 2 = 0) / T 2 + S (otherwise) Qm = Tm (if bm = 0) / Tm + S (otherwise)] y 10 = H(1, Q 1) + r 10 r 1 b 1 = T 1 + y 1 b 1 y 11 = H(1, Q 1 + S) + r 11 ym 0 = H(m, Qm) + rm 0 ym 1 = H(m, Qm + S) + rm 1 (y 10 , y 11 )……. . (ym 0 , ym 1 ) rm bm = Tm + ym bm Random Function H: [m] × {0, 1}k -> {0, 1}l

A little diversion to RO Model >> Love and hate relationship with this model >> Many protocols have proof in RO model which otherwise does not have any proof. >> Real protocol: RO replaced with hash functions >> Protocol analyzed for Security: Hash functions replaced with RO box. >> Proof is for any good? : Existence of such a proof implies the real protocol go wrong only when hash function does not simulate RO. Some proof better than no proof >> Examples: RSA-OEAP (practically in use). CCA-secure extension of RSA >> Finding proof under relatively realistic assumption (e. g. CR) than RO has been very challenging and considered to be great achievement!! Random Function H: [m] × {0, 1}k -> {0, 1}l

Transformation II: OT Extension P 1 P 0 r 11 r 20 r 21 B= [b 1, …bm] r 1 b 1 r 2 b 2 rm 0 rm 1 rm bm Q= [Q 1 = T 1 (if b 1 = 0) / T 1 + S (otherwise) Q 2 = T 2 (if b 2 = 0) / T 2 + S (otherwise) T= [T 1 T 2. Tm] Qm = Tm (if bm = 0) / Tm + S (otherwise)] Random S is known to P 0 only |Ti| = k

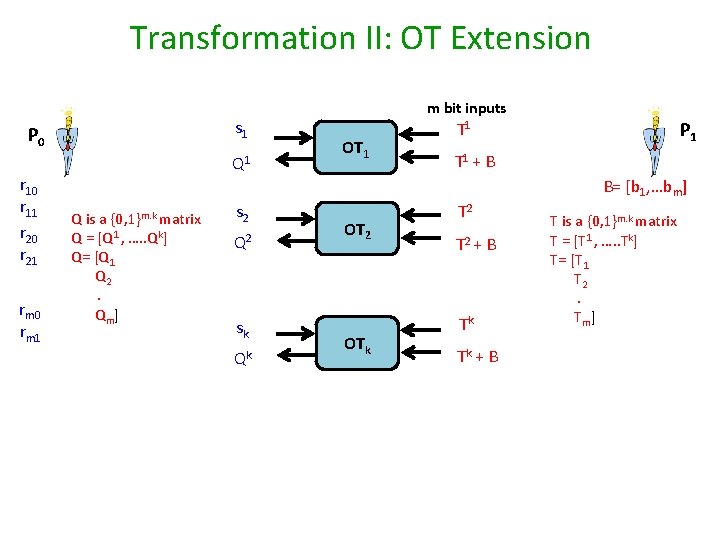
Transformation II: OT Extension s 1 P 0 r 11 r 20 r 21 rm 0 rm 1 Q 1 m bit inputs OT 1 P 1 T 1 + B B= [b 1, …bm] Q is a {0, 1}m. k matrix Q = [Q 1 , …. . Qk] Q= [Q 1 Q 2. Qm] s 2 Q 2 sk Qk OT 2 OTk T 2 + B Tk Tk + B T is a {0, 1}m. k matrix T = [T 1 , …. . Tk] T= [T 1 T 2. Tm]

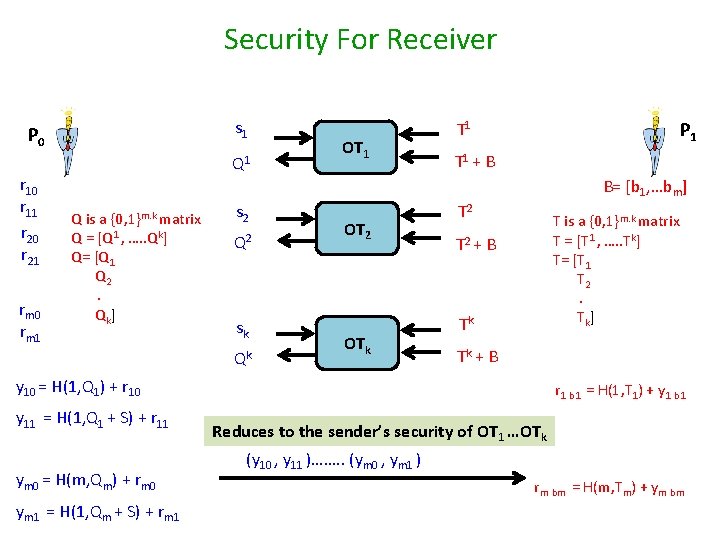
Transformation II: OT Extension s 1 P 0 T[1, 1] + s 1 Q 2 sk T[1, k] + sk T 1 + B B= [b 1, …bm] s 2 T[1, 2] + s 2 OT 1 P 1 T 1 Qk Q= [Q 1 = T 1 (if b 1 = 0) / T 1 + S (otherwise) Q 2 = T 2 (if b 2 = 0) / T 2 + S (otherwise) Qm = Tm (if bm = 0) / Tm + S (otherwise)] OT 2 OTk T 2 + B Tk Tk + B T is a {0, 1}m. k matrix T = [T 1 , …. . Tk] T= [T 1 T 2. Tm]

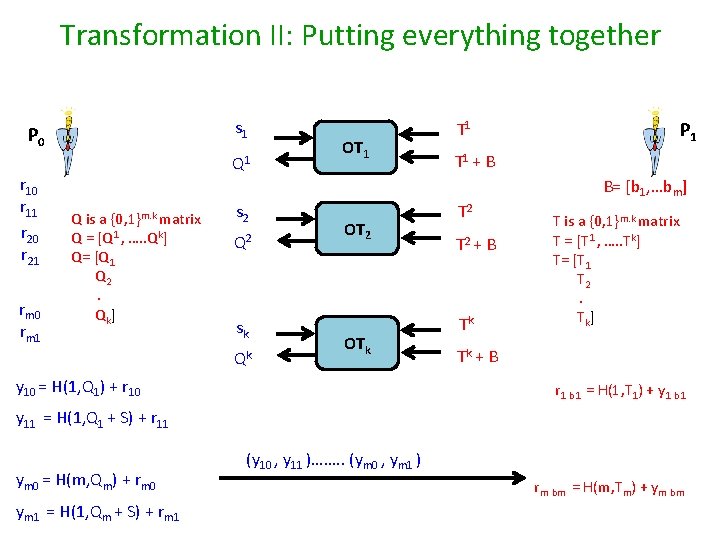
Transformation II: Putting everything together s 1 P 0 r 11 r 20 r 21 rm 0 rm 1 Q 1 OT 1 P 1 T 1 + B B= [b 1, …bm] Q is a {0, 1}m. k matrix Q = [Q 1 , …. . Qk] Q= [Q 1 Q 2. Qk] s 2 Q 2 sk Qk OT 2 OTk y 10 = H(1, Q 1) + r 10 T 2 + B Tk T is a {0, 1}m. k matrix T = [T 1 , …. . Tk] T= [T 1 T 2. Tk] Tk + B r 1 b 1 = H(1, T 1) + y 1 b 1 y 11 = H(1, Q 1 + S) + r 11 ym 0 = H(m, Qm) + rm 0 ym 1 = H(1, Qm + S) + rm 1 (y 10 , y 11 )……. . (ym 0 , ym 1 ) rm bm = H(m, Tm) + ym bm

Roadmap for Building OT Extension [IKNP 03] k bit inputs l bit inputs m (=poly(k)) > k bit inputs OT 1 OT 2 OTk r 10 r 11 r 20 r 21 r 30 r 31 rm 0 rm 1 OT 1 b 1 r 1 b 1 OT 2 b 2 r 2 b 2 OT 3 b 3 r 3 b 3 OTm bm rm bm

Security For Receiver s 1 P 0 r 11 r 20 r 21 rm 0 rm 1 Q 1 OT 1 P 1 T 1 + B B= [b 1, …bm] Q is a {0, 1}m. k matrix Q = [Q 1 , …. . Qk] Q= [Q 1 Q 2. Qk] s 2 Q 2 sk Qk OT 2 OTk T 2 T is a {0, 1}m. k matrix T = [T 1 , …. . Tk] T= [T 1 T 2. Tk] T 2 + B Tk Tk + B y 10 = H(1, Q 1) + r 10 y 11 = H(1, Q 1 + S) + r 11 ym 0 = H(m, Qm) + rm 0 ym 1 = H(1, Qm + S) + rm 1 r 1 b 1 = H(1, T 1) + y 1 b 1 Reduces to the sender’s security of OT 1 …OTk (y 10 , y 11 )……. . (ym 0 , ym 1 ) rm bm = H(m, Tm) + ym bm

Security For Sender [IKNP 03]: Yuval Ishai, Joe Kilian, Kobbi Nissim, and Erez Petrank. Extending oblivious 1 s T P 1 1 Ptransfers 0 efficiently. In CRYPTO , pages 145– 161, 2003. OT 1 1 T 1 + B Q r 10 B= [b 1, …bm] r 11 T 2 s 2 Q is a {0, 1}m. k matrix T is a {0, 1}m. k matrix OT r 20 2 Q = [Q 1 , …. . Qk] T = [T 1 , …. . Tk] Q 2 T 2 + B r 21 Q= [Q 1 T= [T 1 rm 0 rm 1 Q 2. Qk] sk Qk y 10 = H(1, Q 1) + r 10 y 11 = H(1, Q 1 + S) + r 11 ym 0 = H(m, Qm) + rm 0 ym 1 = H(1, Qm + S) + rm 1 OTk Tk T 2. Tk] Tk + B Reduces to the receiver’s security of OT 1 …OTk r 1 b 1 = H(1, T 1) + y 1 b 1 (y 10 , y 11 )……. . (ym 0 , ym 1 ) Reduces to the security of RO except with S=0 rm bm = H(m, Tm) + ym bm

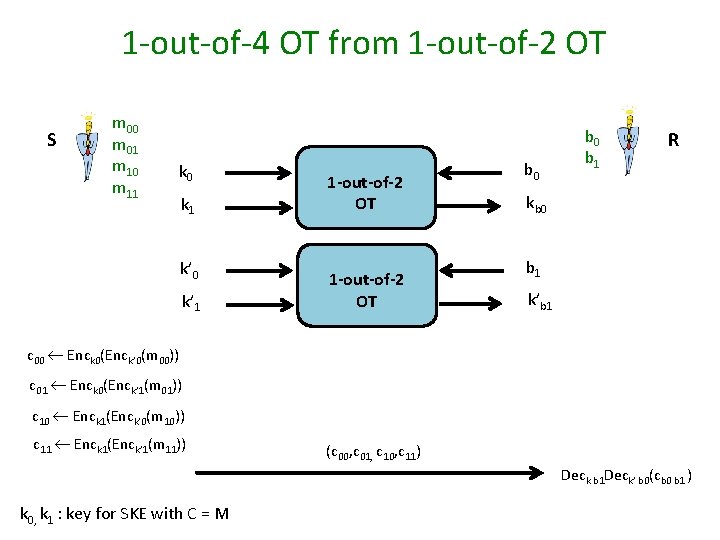
1 -out-of-4 OT from 1 -out-of-2 OT S m 00 m 01 m 10 m 11 k 0 k 1 k’ 0 k’ 1 1 -out-of-2 OT b 0 b 1 R kb 0 b 1 k’b 1 c 00 Enck 0(Enck’ 0(m 00)) c 01 Enck 0(Enck’ 1(m 01)) c 10 Enck 1(Enck’ 0(m 10)) c 11 Enck 1(Enck’ 1(m 11)) (c 00, c 01, c 10, c 11) Deck b 1 Deck’ b 0(cb 0 b 1 ) k 0, k 1 : key for SKE with C = M